2.2 第4课时 二次函数y=ax2+bx+c的图象与性质 课件(共21张PPT)2024-2025学年北师大版九年级数学下册
文档属性
| 名称 | 2.2 第4课时 二次函数y=ax2+bx+c的图象与性质 课件(共21张PPT)2024-2025学年北师大版九年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 18:26:06 | ||
图片预览








文档简介
(共21张PPT)
北师版·九年级下册
第4课时 二次函数y=ax +bx+c的图象与性质
合作探究
问题1 怎样将 y=2x - 4x + 5化成 y = a(x h)2 + k 的形式?
想一想:配方的方法及步骤是什么?
y = 2x - 4x + 5
(1)“提”:提出二次项系数;
(2)“配”:括号内配成完全平方;
(3)“化”:化成顶点式.
提示:配方后的解析式通常称为顶点式.
= 2(x - 2x) + 5
= 2(x - 2x + 1 - 1 ) + 5
= 2(x - 1) + 3
问题2 你能说出 y = 2(x - 1) + 3 的对称轴及顶点坐标吗?
答:对称轴是直线 x = 1,顶点坐标是 (1,3).
问题3 二次函数 y = 2(x - 1) + 3 可以看作是由 y = 2x 怎样平移得到的?
答:平移方法 1:先向上平移 3 个单位,再向右平移 1 个单位得到的;
平移方法 2:先向右平移 1 个单位,再向上平移 3 个单位得到的.
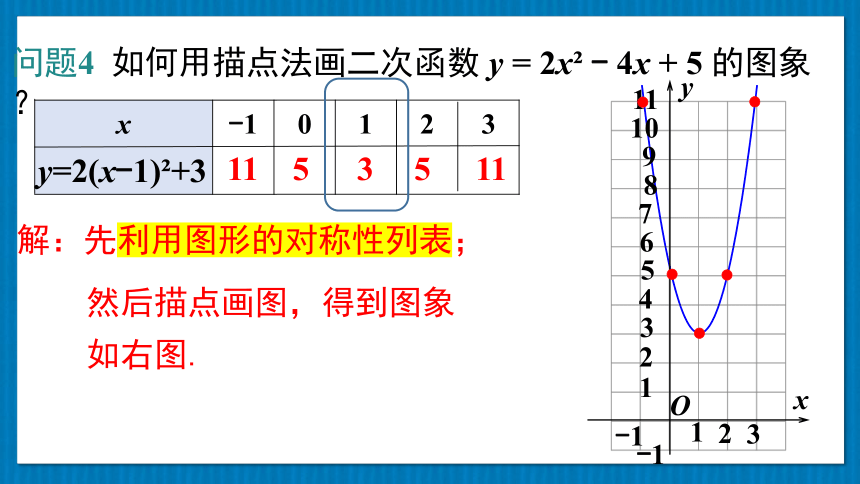
问题4 如何用描点法画二次函数 y = 2x - 4x + 5 的图象?
3
2
1
0
-1
x
解:先利用图形的对称性列表;
11
5
3
5
11
然后描点画图,得到图象
如右图.
y=2(x-1) +3
1
2
x
1
y
O
-1
-1
3
6
2
5
3
4
7
8
9
10
11
问题5 结合二次函数 y = 2x - 4x + 5 的图象,说出其增减性.
当 x<1 时,y 随 x 的增大而减小;
当 x>1 时,y 随 x 的增大而增大.
1
2
x
1
y
O
-1
-1
3
6
2
5
3
4
7
8
9
10
11
典例精析
例1 已知二次函数 y=x2﹣6x + 5.
(1) 将 y=x2﹣6x + 5 化成 y=a(x﹣h)2 + k 的形式;
(2) 求该二次函数的图象的对称轴和顶点坐标;
(3) 当 x 取何值时,y 随 x 的增大而减小?
(3) ∵ 抛物线的开口向上,对称轴是 x=3,
∴ 当 x≤3 时,y 随 x 的增大而减小.
解:(1) y=x2﹣6x + 5=(x﹣3)2﹣4.
(2) 二次函数的图象的对称轴是 x=3,顶点坐标是 (3,-4).
例2 求二次函数y=ax2+bx+c图象的对称轴和顶点坐标.
y = ax2+bx+c
解:把二次函数y=ax2+bx+c的右边配方,得
∴对称轴是 ,顶点坐标为
归纳总结
因此,抛物线 y = ax2 + bx + c 的顶点坐标是
对称轴是直线
,
.
1.一般地,二次函数 y = ax2 + bx + c 可以通过配方化成 y = a(x - h)2 + k 的形式,即
.
二次函数 y = ax2 + bx + c 的顶点式
y = ax2 + bx + c =
根据公式确定下列二次函数图象的对称轴、顶点坐标和最值:
直线 x=3
直线 x=8
直线 x=1.25
直线 x= 0.5
最小值-5
最大值1
最小值
最大值
2
二次函数的图象与系数的关系
想一想,对于二次函数 y = ax2 + bx + c (a≠0)
图象性质中,字母 a,b,c 所起的作用.
开口方向
一般研究哪几种性质?
顶点坐标
对称轴
增减性
a 决定
a,b 共同决定
开口方向,对称轴
a,b 共同决定
c 决定什么?
合作探究
x
y
O
问题 二次函数 y = ax2 + bx + c 的图象如下图所示,请根据二次函数的性质填空:
a1 ___0
b1 ___0
c1 ___0
a2 ___0
b2 ___0
c2 ___0
>
>
>
>
<
=
x = 0 时
y = c.
y2 = a2x2 + b2x + c2
y1=a1x2+b1x+c1
x
y
O
a3 ___ 0
b3 ___ 0
c3 ___ 0
a4 ___ 0
b4 ___ 0
c4 ___ 0
<
=
>
<
>
<
x = 0时
y = c.
y4 = a4x2 + b4x + c4
y3 = a3x2 + b3x + c3
字母符号 图象的特征
a>0 开口___________
a<0 开口___________
b = 0 对称轴为_____轴
a、b 同号(ab>0) 对称轴在 y 轴的____侧
a、b 异号(ab<0) 对称轴在 y 轴的____侧
c = 0 经过原点
c > 0 与 y 轴交于_____半轴
c < 0 与 y 轴交于_____半轴
向上
向下
y
左
右
正
负
二次函数图象与 a、b、c 的关系
O
y
x
–1
–2
3
已知二次函数 y = ax2+bx+c(a≠0)的图象如图所示,则下列结论:
(1)a、b 同号;
(2)当 x = –1和 x = 3 时,函数值相等;
(3) 4a+b = 0;
(4)当 y = –2 时,x 的值只能取 0;
其中正确的是 .
直线x=1
(2)
链接中考
1. (浙江)如图,已知二次函数 y=ax2+bx+c 图象的对称轴为直线 x=-1,下列结论: ①abc<0;②3a<-c;
③若 m 为任意实数,则有 a - bm<am2 + b;
④若图象经过点(-3,-2),方程 a2 + bx + c + 2 = 0
的两根为 x1,x2 ( | x1 |<| x2 | ),则 2x1-x2 = 5.
其中正确的结论的个数是 ( )
A.1 B.2
C.3 D.4
O
x = -1
1
x
y
【解析】解:①:由图象可知:a<0,c>0, ,
∴ b = 2a<0,∴ abc>0,故 ① 错误;
②:当 x = 1 时,y = a + b + c = a + 2a + c = 3a + c<0,
∴3a<-c,故 ② 正确;
③:∵ x = -1 时,y 有最大值,
∴ a - b + c≥am2 + bm + c ( m 为任意实数),
即 a - b≥am2 + bm,即 a - bm≥am2 + b.
故 ③ 错误;
O
x = -1
1
x
y
④:∵二次函数 y=ax2+bx+c (a≠0) 图象经过点
(-3,-2),方程 ax2+bx+c+2 = 0 的两根
为 x1,x2 ( | x1 |<| x2 | ),
∴二次函数 y=ax2+bx+c 与直线 y = -2 的一个交点
为 (-3,-2).
∵抛物线的对称轴为直线 x=-1,
∴二次函数 y=ax2+bx+c 与直线 y = -2 的
另一个交点为 (1,-2),即 x1 = 1,x2 = -3.
∴2x1-x2 = 2-(-3) = 5,故 ④ 正确.
所以正确的是 ②④.
O
x = -1
1
x
y
顶点:
对称轴:
y = ax2+bx+c ( a ≠ 0 )
(一般式)
配方法
公式法
(顶点式)
课堂小结
课堂小结
谈一谈你的收获!
二次函数y=ax +bx+c的图象是一条抛物线.
顶点坐标公式
对称轴是 ,顶点坐标为
课后作业
课后练习
课后练习
1.确定下列抛物线的开口方向、对称轴及顶点坐标.
(1)y=-3x2+12x-3; (2)y=4x2-24x+26;
(3)y=2x2+8x-6; (4)y= x2-2x-1.
开口向上,
对称轴为x=3,
顶点为(3, - 10).
开口向下,
对称轴为x=2,
顶点为(2,9).
开口向上,
对称轴为x=-2
顶点为( - 2, - 14).
开口向上,
对称轴为x=2,
顶点为(2, - 3).
北师版·九年级下册
第4课时 二次函数y=ax +bx+c的图象与性质
合作探究
问题1 怎样将 y=2x - 4x + 5化成 y = a(x h)2 + k 的形式?
想一想:配方的方法及步骤是什么?
y = 2x - 4x + 5
(1)“提”:提出二次项系数;
(2)“配”:括号内配成完全平方;
(3)“化”:化成顶点式.
提示:配方后的解析式通常称为顶点式.
= 2(x - 2x) + 5
= 2(x - 2x + 1 - 1 ) + 5
= 2(x - 1) + 3
问题2 你能说出 y = 2(x - 1) + 3 的对称轴及顶点坐标吗?
答:对称轴是直线 x = 1,顶点坐标是 (1,3).
问题3 二次函数 y = 2(x - 1) + 3 可以看作是由 y = 2x 怎样平移得到的?
答:平移方法 1:先向上平移 3 个单位,再向右平移 1 个单位得到的;
平移方法 2:先向右平移 1 个单位,再向上平移 3 个单位得到的.
问题4 如何用描点法画二次函数 y = 2x - 4x + 5 的图象?
3
2
1
0
-1
x
解:先利用图形的对称性列表;
11
5
3
5
11
然后描点画图,得到图象
如右图.
y=2(x-1) +3
1
2
x
1
y
O
-1
-1
3
6
2
5
3
4
7
8
9
10
11
问题5 结合二次函数 y = 2x - 4x + 5 的图象,说出其增减性.
当 x<1 时,y 随 x 的增大而减小;
当 x>1 时,y 随 x 的增大而增大.
1
2
x
1
y
O
-1
-1
3
6
2
5
3
4
7
8
9
10
11
典例精析
例1 已知二次函数 y=x2﹣6x + 5.
(1) 将 y=x2﹣6x + 5 化成 y=a(x﹣h)2 + k 的形式;
(2) 求该二次函数的图象的对称轴和顶点坐标;
(3) 当 x 取何值时,y 随 x 的增大而减小?
(3) ∵ 抛物线的开口向上,对称轴是 x=3,
∴ 当 x≤3 时,y 随 x 的增大而减小.
解:(1) y=x2﹣6x + 5=(x﹣3)2﹣4.
(2) 二次函数的图象的对称轴是 x=3,顶点坐标是 (3,-4).
例2 求二次函数y=ax2+bx+c图象的对称轴和顶点坐标.
y = ax2+bx+c
解:把二次函数y=ax2+bx+c的右边配方,得
∴对称轴是 ,顶点坐标为
归纳总结
因此,抛物线 y = ax2 + bx + c 的顶点坐标是
对称轴是直线
,
.
1.一般地,二次函数 y = ax2 + bx + c 可以通过配方化成 y = a(x - h)2 + k 的形式,即
.
二次函数 y = ax2 + bx + c 的顶点式
y = ax2 + bx + c =
根据公式确定下列二次函数图象的对称轴、顶点坐标和最值:
直线 x=3
直线 x=8
直线 x=1.25
直线 x= 0.5
最小值-5
最大值1
最小值
最大值
2
二次函数的图象与系数的关系
想一想,对于二次函数 y = ax2 + bx + c (a≠0)
图象性质中,字母 a,b,c 所起的作用.
开口方向
一般研究哪几种性质?
顶点坐标
对称轴
增减性
a 决定
a,b 共同决定
开口方向,对称轴
a,b 共同决定
c 决定什么?
合作探究
x
y
O
问题 二次函数 y = ax2 + bx + c 的图象如下图所示,请根据二次函数的性质填空:
a1 ___0
b1 ___0
c1 ___0
a2 ___0
b2 ___0
c2 ___0
>
>
>
>
<
=
x = 0 时
y = c.
y2 = a2x2 + b2x + c2
y1=a1x2+b1x+c1
x
y
O
a3 ___ 0
b3 ___ 0
c3 ___ 0
a4 ___ 0
b4 ___ 0
c4 ___ 0
<
=
>
<
>
<
x = 0时
y = c.
y4 = a4x2 + b4x + c4
y3 = a3x2 + b3x + c3
字母符号 图象的特征
a>0 开口___________
a<0 开口___________
b = 0 对称轴为_____轴
a、b 同号(ab>0) 对称轴在 y 轴的____侧
a、b 异号(ab<0) 对称轴在 y 轴的____侧
c = 0 经过原点
c > 0 与 y 轴交于_____半轴
c < 0 与 y 轴交于_____半轴
向上
向下
y
左
右
正
负
二次函数图象与 a、b、c 的关系
O
y
x
–1
–2
3
已知二次函数 y = ax2+bx+c(a≠0)的图象如图所示,则下列结论:
(1)a、b 同号;
(2)当 x = –1和 x = 3 时,函数值相等;
(3) 4a+b = 0;
(4)当 y = –2 时,x 的值只能取 0;
其中正确的是 .
直线x=1
(2)
链接中考
1. (浙江)如图,已知二次函数 y=ax2+bx+c 图象的对称轴为直线 x=-1,下列结论: ①abc<0;②3a<-c;
③若 m 为任意实数,则有 a - bm<am2 + b;
④若图象经过点(-3,-2),方程 a2 + bx + c + 2 = 0
的两根为 x1,x2 ( | x1 |<| x2 | ),则 2x1-x2 = 5.
其中正确的结论的个数是 ( )
A.1 B.2
C.3 D.4
O
x = -1
1
x
y
【解析】解:①:由图象可知:a<0,c>0, ,
∴ b = 2a<0,∴ abc>0,故 ① 错误;
②:当 x = 1 时,y = a + b + c = a + 2a + c = 3a + c<0,
∴3a<-c,故 ② 正确;
③:∵ x = -1 时,y 有最大值,
∴ a - b + c≥am2 + bm + c ( m 为任意实数),
即 a - b≥am2 + bm,即 a - bm≥am2 + b.
故 ③ 错误;
O
x = -1
1
x
y
④:∵二次函数 y=ax2+bx+c (a≠0) 图象经过点
(-3,-2),方程 ax2+bx+c+2 = 0 的两根
为 x1,x2 ( | x1 |<| x2 | ),
∴二次函数 y=ax2+bx+c 与直线 y = -2 的一个交点
为 (-3,-2).
∵抛物线的对称轴为直线 x=-1,
∴二次函数 y=ax2+bx+c 与直线 y = -2 的
另一个交点为 (1,-2),即 x1 = 1,x2 = -3.
∴2x1-x2 = 2-(-3) = 5,故 ④ 正确.
所以正确的是 ②④.
O
x = -1
1
x
y
顶点:
对称轴:
y = ax2+bx+c ( a ≠ 0 )
(一般式)
配方法
公式法
(顶点式)
课堂小结
课堂小结
谈一谈你的收获!
二次函数y=ax +bx+c的图象是一条抛物线.
顶点坐标公式
对称轴是 ,顶点坐标为
课后作业
课后练习
课后练习
1.确定下列抛物线的开口方向、对称轴及顶点坐标.
(1)y=-3x2+12x-3; (2)y=4x2-24x+26;
(3)y=2x2+8x-6; (4)y= x2-2x-1.
开口向上,
对称轴为x=3,
顶点为(3, - 10).
开口向下,
对称轴为x=2,
顶点为(2,9).
开口向上,
对称轴为x=-2
顶点为( - 2, - 14).
开口向上,
对称轴为x=2,
顶点为(2, - 3).
