1.3人人都能学会数学课时提升作业(含解析)
文档属性
| 名称 | 1.3人人都能学会数学课时提升作业(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 96.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-30 00:00:00 | ||
图片预览

文档简介
1.3人人都能学会数学课时提升作业(含解析)
一、选择题(每小题4分,共12分)
1.某中学随机地调查了50名学生,了解他们一周在校的体育锻炼时间,结果如表所示:
时间(h) 5 6 7 8
人数 10 15 20 5
则这50名学生这一周在校的平均体育锻炼时间是( )
A.6.2 h B.6.4 h C.6.5 h D.7 h
【解析】选B.由题意得这50名学生这一周在校的平均体育锻炼时间是
=6.4(h).
【知识拓展】求平均数的方法
一般地,在n个数据中,如果数据x1出现f1次,x2出现f2次,x3出现f3次,…,xn出现fn次,且f1+f2+f3+…+fn=n,那么这n个数据的平均数
2.如图,将四个长为16 cm,宽为2 cm的长方形平放在桌面上,若夹角都是直角,则桌面被盖住的面积是( )
A.72 cm2 B.128 cm2
C.20 cm2 D.112 cm2
【解析】选D.桌面被盖住的面积,就是图中这个组合图形的面积:四个长方形的面积之和减去重叠部分的4个边长为2 cm的小正方形的面积,即16×2×4-2×2×4=128-16=112(cm2).
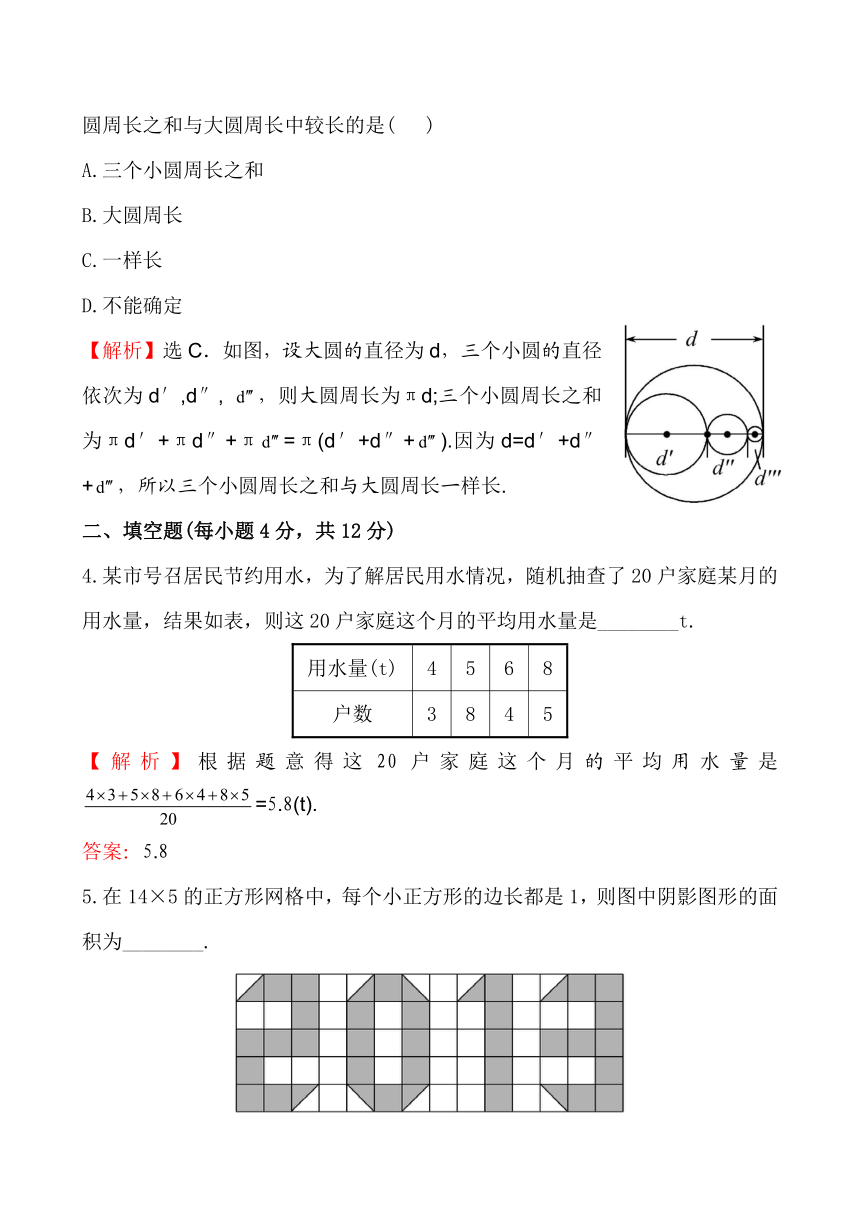
3.如图所示,四个圆的圆心在同一条直线上,则三个小圆周长之和与大圆周长中较长的是( )
A.三个小圆周长之和
B.大圆周长
C.一样长
D.不能确定
【解析】选C.如图,设大圆的直径为d,三个小圆的直径依次为d′,d″, ,则大圆周长为πd;三个小圆周长之和为πd′+πd″+π=π(d′+d″+).因为d=d′+d″+,所以三个小圆周长之和与大圆周长一样长.
二、填空题(每小题4分,共12分)
4.某市号召居民节约用水,为了解居民用水情况,随机抽查了20户家庭某月的用水量,结果如表,则这20户家庭这个月的平均用水量是________t.
用水量(t) 4 5 6 8
户数 3 8 4 5
【解析】根据题意得这20户家庭这个月的平均用水量是=5.8(t).
答案:5.8
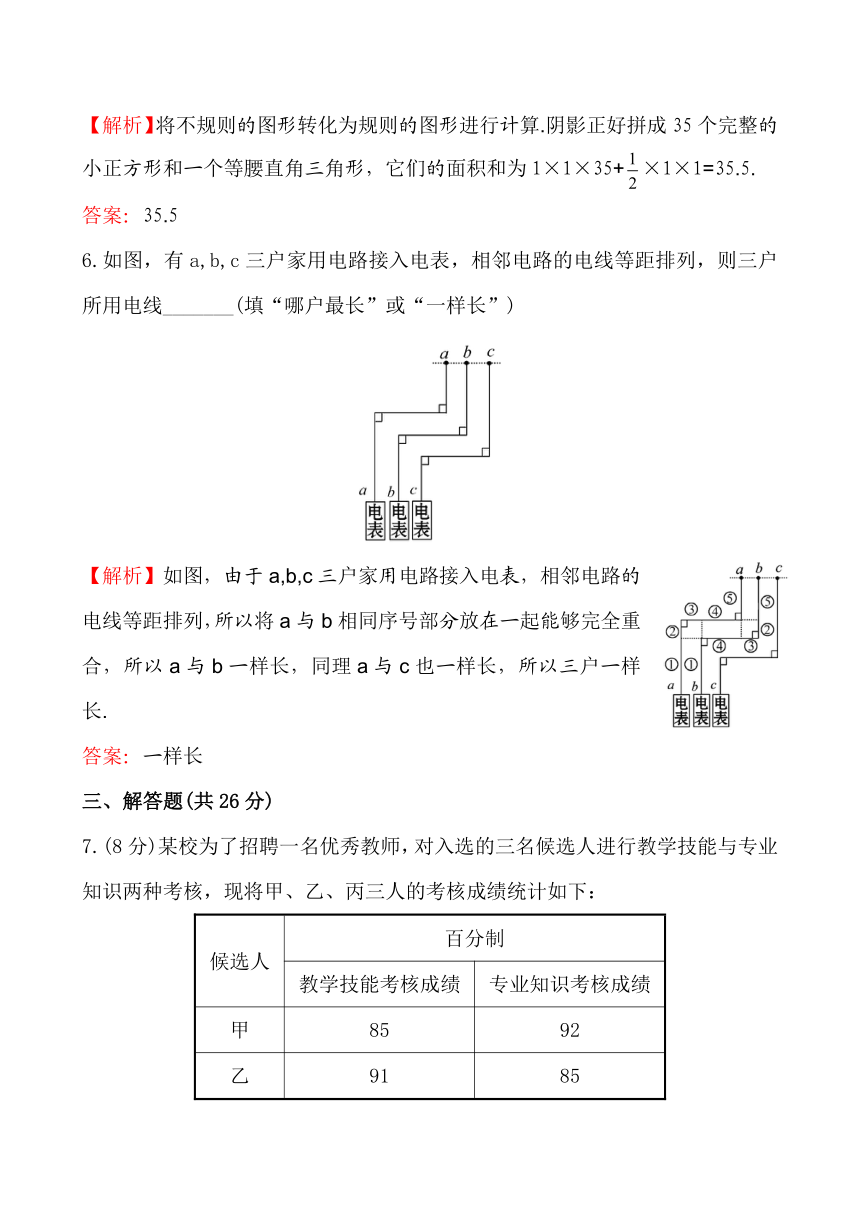
5.在14×5的正方形网格中,每个小正方形的边长都是1,则图中阴影图形的面积为________.
【解析】将不规则的图形转化为规则的图形进行计算.阴影正好拼成35个完整的小正方形和一个等腰直角三角形,它们的面积和为1×1×35+×1×1=35.5.
答案:35.5
6.如图,有a,b,c三户家用电路接入电表,相邻电路的电线等距排列,则三户所用电线_______(填“哪户最长”或“一样长”)
【解析】如图,由于a,b,c三户家用电路接入电表,相邻电路的电线等距排列,所以将a与b相同序号部分放在一起能够完全重合,所以a与b一样长,同理a与c也一样长,所以三户一样长.
答案:一样长
三、解答题(共26分)
7.(8分)某校为了招聘一名优秀教师,对入选的三名候选人进行教学技能与专业知识两种考核,现将甲、乙、丙三人的考核成绩统计如下:
候选人 百分制
教学技能考核成绩 专业知识考核成绩
甲 85 92
乙 91 85
丙 80 90
(1)如果校方认为教师的教学技能水平与专业知识水平同等重要,则候选人将_____被录取.
(2)如果校方认为教师的教学技能水平比专业知识水平重要,因此分别赋予它们6和4的权.计算它们赋权后各自的平均成绩,并说明谁将被录取.
【解析】(1)甲
(2)甲的平均成绩为:(85×6+92×4)÷10=87.8(分).
乙的平均成绩为:(91×6+85×4)÷10=88.6(分).
丙的平均成绩为:(80×6+90×4)÷10=84(分).
乙的平均分数最高,所以乙将被录取.
【变式训练】在全国青年歌手大赛中,规定每位选手的最后得分是从所有评委给出的分数中去掉一个最低分和一个最高分,计算其余分数的平均分,现在三位歌手的得分情况如下:
A:9.2,8.5,8.6,9.0,8.3,8.7
B:8.9,8.8,8.8,8.7,8.5,9.0
C:7.9,8.0,8.0,8.6,8.5,8.5
三位歌手最后得分是多少?
【解析】A的得分为(8.5+8.6+9.0+8.7)÷4=8.7(分),
B的得分为(8.9+8.8+8.8+8.7)÷4=8.8(分),
C的得分为(8.0+8.0+8.5+8.5)÷4=8.25(分),
所以三位歌手最后得分为A.8.7分,B.8.8分,C.8.25分.
8.(8分)某学校准备在升旗台的台阶上铺设一种红色的地毯(含台阶的最上层),已知这种地毯的批发价为每平方米40元,升旗台的台阶宽为3 m,其侧面如图所示,请你帮助测算一下,买地毯至少需要多少元?
【解析】想象:把楼梯横的台阶向上与最高处拉平,竖的台阶左边的向左,右边的向右拉直构成一个长方形,长、宽分别为6.4 m,3.8 m,所以地毯的长度为6.4+3.8+3.8=14(m),地毯的面积为14×3=42(m2),所以买地毯至少需要42×40=1 680(元).
答:买地毯至少需要1 680元.
【知识归纳】台阶问题中的转化思想
台阶问题解题过程渗透着转化思想,除此之外,很多问题通过由陌生向熟悉、由复杂向简单的转化后,得以顺利解决.例如,
(1)已知台阶的长和高,计算台阶的总长时,常把求台阶总长这一复杂问题转化为我们熟悉的求长方形的长和宽问题.
(2)已知台阶的长和高,计算台阶上所铺地毯的面积时,常把求台阶多个面的面积和这一繁琐过程转化为求一个长方形面积的简单过程.
【培优训练】
9.(10分)2014年5月1日小明和爸爸一起去旅游,在火车站看到如表所示的列车时刻表:
2014年5月1日××次列车时刻表
始发点 发车时间 终点站 到站时间
A站 上午8:20 B站 次日12:20
小明的爸爸用手机上网找到了以前同一车次的时刻表如下:
2006年12月15日××次列车时刻表
始发点 发车时间 终点站 到站时间
A站 下午14:30 B站 第三日8:30
比较了两张时刻表后,小明的爸爸提出了如下两个问题,请你帮小明解答:
(1)现在该次列车的运行时间比以前缩短了多少小时?
(2)若该次列车提速后的平均时速为每小时200 km,那么,该次列车原来的平均时速为多少?(结果四舍五入到个位)
【解析】(1)原来该次列车所用时间=2×24+8.5-14.5=42(h).现在该次列车的运行时间=24+12-8=28(h),42-28=14(h),所以缩短了14 h.
(2)28×200÷42≈133(km).
答:(1)现在该次列车的运行时间比以前缩短了14 h.
(2)原来的平均时速约为133 km/h.
一、选择题(每小题4分,共12分)
1.某中学随机地调查了50名学生,了解他们一周在校的体育锻炼时间,结果如表所示:
时间(h) 5 6 7 8
人数 10 15 20 5
则这50名学生这一周在校的平均体育锻炼时间是( )
A.6.2 h B.6.4 h C.6.5 h D.7 h
【解析】选B.由题意得这50名学生这一周在校的平均体育锻炼时间是
=6.4(h).
【知识拓展】求平均数的方法
一般地,在n个数据中,如果数据x1出现f1次,x2出现f2次,x3出现f3次,…,xn出现fn次,且f1+f2+f3+…+fn=n,那么这n个数据的平均数
2.如图,将四个长为16 cm,宽为2 cm的长方形平放在桌面上,若夹角都是直角,则桌面被盖住的面积是( )
A.72 cm2 B.128 cm2
C.20 cm2 D.112 cm2
【解析】选D.桌面被盖住的面积,就是图中这个组合图形的面积:四个长方形的面积之和减去重叠部分的4个边长为2 cm的小正方形的面积,即16×2×4-2×2×4=128-16=112(cm2).
3.如图所示,四个圆的圆心在同一条直线上,则三个小圆周长之和与大圆周长中较长的是( )
A.三个小圆周长之和
B.大圆周长
C.一样长
D.不能确定
【解析】选C.如图,设大圆的直径为d,三个小圆的直径依次为d′,d″, ,则大圆周长为πd;三个小圆周长之和为πd′+πd″+π=π(d′+d″+).因为d=d′+d″+,所以三个小圆周长之和与大圆周长一样长.
二、填空题(每小题4分,共12分)
4.某市号召居民节约用水,为了解居民用水情况,随机抽查了20户家庭某月的用水量,结果如表,则这20户家庭这个月的平均用水量是________t.
用水量(t) 4 5 6 8
户数 3 8 4 5
【解析】根据题意得这20户家庭这个月的平均用水量是=5.8(t).
答案:5.8
5.在14×5的正方形网格中,每个小正方形的边长都是1,则图中阴影图形的面积为________.
【解析】将不规则的图形转化为规则的图形进行计算.阴影正好拼成35个完整的小正方形和一个等腰直角三角形,它们的面积和为1×1×35+×1×1=35.5.
答案:35.5
6.如图,有a,b,c三户家用电路接入电表,相邻电路的电线等距排列,则三户所用电线_______(填“哪户最长”或“一样长”)
【解析】如图,由于a,b,c三户家用电路接入电表,相邻电路的电线等距排列,所以将a与b相同序号部分放在一起能够完全重合,所以a与b一样长,同理a与c也一样长,所以三户一样长.
答案:一样长
三、解答题(共26分)
7.(8分)某校为了招聘一名优秀教师,对入选的三名候选人进行教学技能与专业知识两种考核,现将甲、乙、丙三人的考核成绩统计如下:
候选人 百分制
教学技能考核成绩 专业知识考核成绩
甲 85 92
乙 91 85
丙 80 90
(1)如果校方认为教师的教学技能水平与专业知识水平同等重要,则候选人将_____被录取.
(2)如果校方认为教师的教学技能水平比专业知识水平重要,因此分别赋予它们6和4的权.计算它们赋权后各自的平均成绩,并说明谁将被录取.
【解析】(1)甲
(2)甲的平均成绩为:(85×6+92×4)÷10=87.8(分).
乙的平均成绩为:(91×6+85×4)÷10=88.6(分).
丙的平均成绩为:(80×6+90×4)÷10=84(分).
乙的平均分数最高,所以乙将被录取.
【变式训练】在全国青年歌手大赛中,规定每位选手的最后得分是从所有评委给出的分数中去掉一个最低分和一个最高分,计算其余分数的平均分,现在三位歌手的得分情况如下:
A:9.2,8.5,8.6,9.0,8.3,8.7
B:8.9,8.8,8.8,8.7,8.5,9.0
C:7.9,8.0,8.0,8.6,8.5,8.5
三位歌手最后得分是多少?
【解析】A的得分为(8.5+8.6+9.0+8.7)÷4=8.7(分),
B的得分为(8.9+8.8+8.8+8.7)÷4=8.8(分),
C的得分为(8.0+8.0+8.5+8.5)÷4=8.25(分),
所以三位歌手最后得分为A.8.7分,B.8.8分,C.8.25分.
8.(8分)某学校准备在升旗台的台阶上铺设一种红色的地毯(含台阶的最上层),已知这种地毯的批发价为每平方米40元,升旗台的台阶宽为3 m,其侧面如图所示,请你帮助测算一下,买地毯至少需要多少元?
【解析】想象:把楼梯横的台阶向上与最高处拉平,竖的台阶左边的向左,右边的向右拉直构成一个长方形,长、宽分别为6.4 m,3.8 m,所以地毯的长度为6.4+3.8+3.8=14(m),地毯的面积为14×3=42(m2),所以买地毯至少需要42×40=1 680(元).
答:买地毯至少需要1 680元.
【知识归纳】台阶问题中的转化思想
台阶问题解题过程渗透着转化思想,除此之外,很多问题通过由陌生向熟悉、由复杂向简单的转化后,得以顺利解决.例如,
(1)已知台阶的长和高,计算台阶的总长时,常把求台阶总长这一复杂问题转化为我们熟悉的求长方形的长和宽问题.
(2)已知台阶的长和高,计算台阶上所铺地毯的面积时,常把求台阶多个面的面积和这一繁琐过程转化为求一个长方形面积的简单过程.
【培优训练】
9.(10分)2014年5月1日小明和爸爸一起去旅游,在火车站看到如表所示的列车时刻表:
2014年5月1日××次列车时刻表
始发点 发车时间 终点站 到站时间
A站 上午8:20 B站 次日12:20
小明的爸爸用手机上网找到了以前同一车次的时刻表如下:
2006年12月15日××次列车时刻表
始发点 发车时间 终点站 到站时间
A站 下午14:30 B站 第三日8:30
比较了两张时刻表后,小明的爸爸提出了如下两个问题,请你帮小明解答:
(1)现在该次列车的运行时间比以前缩短了多少小时?
(2)若该次列车提速后的平均时速为每小时200 km,那么,该次列车原来的平均时速为多少?(结果四舍五入到个位)
【解析】(1)原来该次列车所用时间=2×24+8.5-14.5=42(h).现在该次列车的运行时间=24+12-8=28(h),42-28=14(h),所以缩短了14 h.
(2)28×200÷42≈133(km).
答:(1)现在该次列车的运行时间比以前缩短了14 h.
(2)原来的平均时速约为133 km/h.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
