人教版九年级上册数学22.3 实际问题与二次函数 课件(共19张PPT)
文档属性
| 名称 | 人教版九年级上册数学22.3 实际问题与二次函数 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 19.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-07 13:29:38 | ||
图片预览





文档简介
(共19张PPT)
实际问题与二次函数
——抛物线形拱桥
人教版数学 九年级上册
目前世界上跨度最大的铁路拱桥
——怒江四线特大桥
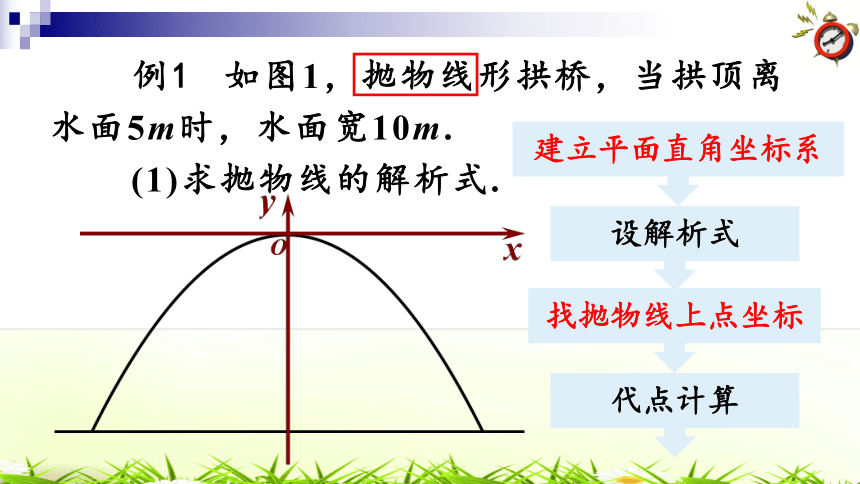
例1 如图1,抛物线形拱桥,当拱顶离水面5m时,水面宽10m.
(1)求抛物线的解析式.
待定系数法
设解析式
代点计算
平面直角坐标系
图1
例1 如图1,抛物线形拱桥,当拱顶离水面5m时,水面宽10m.
(1)求抛物线的解析式.
建立平面直角坐标系
设解析式
找抛物线上点坐标
代点计算
(2)桥下有一条高3m,宽6m的货船.
该船能否从桥下通过?(假设船底与水面齐平)
6
3
任务 2min小组讨论,完成解答.
水涨船高
船过不去了
船
船
(3)如果水面上涨1m,那么高3m,宽6m的货船是否还能从桥下通过? (假设船底与水面齐平)
6
3
1
(4)当水面下降1m时,这条宽6m的船,要想从桥下通过,则船的最大高度为多少米 (假设船底与水面齐平)
6
练习:如图,抛物线形拱桥,当拱顶离水面2m时,一条宽2m,高1.5m的船恰好能通过,此时水面宽多少米? (假设船底与水面齐平)
船过拱桥
数学问题
的解
数学问题
抽象
建系
找抛物线上的点
求解析式
判断宽或高
解释
设解析式
课堂小结
☆课后探究
例1中若建立如图所示的平面直角坐标系,答案是否一样?
1.如图所示,有一座抛物线型拱桥,在正常水位AB时,水面宽20米,水位上升3米,就达到警戒线CD,这时水面宽为10米。
(1)求抛物线型拱桥的解析式.
(2)若洪水到来时,水位以每小时0.2米的速度上升,从警戒线开始,再持续多少小时就能达到拱桥顶?
(3)在正常水位时,有一艘宽8米,高2.5米的小船能否安全通过这座桥?
A
B
C
D
2.查阅资料,了解抛物线形建筑的优点.
3.某公司需要在两山之间的峡谷上修建一做抛物线形拱桥,桥下是一条宽100米的河流,河面距所要架设的拱桥的高度是50米,请你根据题意给出设计图稿.
数学与生活息息相关
希望通过今天的学习
你能用数学的眼光去看世界
实际问题与二次函数
——抛物线形拱桥
人教版数学 九年级上册
目前世界上跨度最大的铁路拱桥
——怒江四线特大桥
例1 如图1,抛物线形拱桥,当拱顶离水面5m时,水面宽10m.
(1)求抛物线的解析式.
待定系数法
设解析式
代点计算
平面直角坐标系
图1
例1 如图1,抛物线形拱桥,当拱顶离水面5m时,水面宽10m.
(1)求抛物线的解析式.
建立平面直角坐标系
设解析式
找抛物线上点坐标
代点计算
(2)桥下有一条高3m,宽6m的货船.
该船能否从桥下通过?(假设船底与水面齐平)
6
3
任务 2min小组讨论,完成解答.
水涨船高
船过不去了
船
船
(3)如果水面上涨1m,那么高3m,宽6m的货船是否还能从桥下通过? (假设船底与水面齐平)
6
3
1
(4)当水面下降1m时,这条宽6m的船,要想从桥下通过,则船的最大高度为多少米 (假设船底与水面齐平)
6
练习:如图,抛物线形拱桥,当拱顶离水面2m时,一条宽2m,高1.5m的船恰好能通过,此时水面宽多少米? (假设船底与水面齐平)
船过拱桥
数学问题
的解
数学问题
抽象
建系
找抛物线上的点
求解析式
判断宽或高
解释
设解析式
课堂小结
☆课后探究
例1中若建立如图所示的平面直角坐标系,答案是否一样?
1.如图所示,有一座抛物线型拱桥,在正常水位AB时,水面宽20米,水位上升3米,就达到警戒线CD,这时水面宽为10米。
(1)求抛物线型拱桥的解析式.
(2)若洪水到来时,水位以每小时0.2米的速度上升,从警戒线开始,再持续多少小时就能达到拱桥顶?
(3)在正常水位时,有一艘宽8米,高2.5米的小船能否安全通过这座桥?
A
B
C
D
2.查阅资料,了解抛物线形建筑的优点.
3.某公司需要在两山之间的峡谷上修建一做抛物线形拱桥,桥下是一条宽100米的河流,河面距所要架设的拱桥的高度是50米,请你根据题意给出设计图稿.
数学与生活息息相关
希望通过今天的学习
你能用数学的眼光去看世界
同课章节目录
