人教版八年级数学学科2024年秋季学期期中学业评估数学试题(含答案)
文档属性
| 名称 | 人教版八年级数学学科2024年秋季学期期中学业评估数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 827.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 08:39:25 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024年秋季学期八年级第一阶段学业评估数学试题
本试卷共6页,24 个小题,满分120分,考试用时120分钟
★祝考试顺利★
注意事项:
1.考生答题全部在答题卷上,答在试题卷上无效。
2.请认真核对监考教师在答题卷上所粘贴条形码的姓名、准考证号码是否与本人相符合,再将自己的姓名、准考证号码用0.5毫米的黑色墨水签字笔填写在答题卷及试题卷上。
3.选择题作答必须用2B铅笔将答题卷上对应的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案,非选择题作答必须用0.5毫米黑色墨水签字笔写在答题卷上指定位置,在其他位置答题一律无效。
4.作图必须用2B铅笔作答,并请加黑加粗,描写清楚。
5.考生不得折叠答题卷,保持答题卷的整洁.考试结束后,请将试题卷和答题卷一并上交。
一、选择题(本大题共有10个小题,每小题3分,共30分.在每小题给出的四个选项中,
只有一项是符合题目要求的,请将正确选择项前的字母代号填涂在答题卷相应位置上)
1.下列长度的三根小木棒,不能摆成三角形的是( )
A.6cm,6cm,13cm B.5cm,7cm,11cm C.9cm,6cm,8cm D.3cm,4cm,5cm
2.下列图形中是轴对称图形的是( )
A. B. C. D.
3.如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )
A.∠B=∠C B.BE=CD C.BD=CE D.∠ADC=∠AEB
4.如图,∠BAC=140°,若DM和EN分别垂直平分AB和AC,则∠DAE等于( )
A.100° B.90° C.80° D.70°
5.如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E,∠A=∠ABE,BD=1,BC=3,则AC的长为( )
A.4 B.4.5 C.5 D.5.5
3题图 4题图 5题图
6.某商店出售下列四种形状的地砖:①正三角形;②正方形;③正五边形;④正六边形.
若只选购其中一种地砖镶嵌地面,可供选择的地砖共有( )
A.4种 B.3种 C.2种 D.1种
7.如图,在△ABC中,AB=AC,∠A=36°,点D,P分别是图中所作直线和射线与AB,CD的交点.根据图中尺规作图的痕迹推断,以下结论错误的是( )
A.∠ABP=∠A B.AD=CD C.∠PBC=∠ACD D.∠BPC=118°
8.如图,将正五边形纸片ABCDE折叠,使点B与点E重合,折痕为AM,展开后,再将纸片折叠,使边AB落在线段AM上,点B的对应点为点B',折痕为AF,则∠AFB'=( )度.
A.45 B.36 C.54 D.48
9.如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为点N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则DE的长是( )
A.6 B.4 C.2 D.5
10.如图,△ABC中,AD⊥BC交BC于D,AE平分∠BAC交BC于E,F为BC的延长线上一点,FG⊥AE交AD的延长线于G,AC的延长线交FG于H,连接BG,下列结论:
①∠DAE=∠F; ②2∠DAE=∠ABD﹣∠ACE; ③S△AEB:S△AEC=AB:AC;
④∠AGH=∠BAE+∠ACB.其中正确的结论有( )个.
A.1 B.2 C.3 D.4
7题图 8题图 9题图 10题图
二、填空题(本大题共有5小题,每小题3分,共15分.不要求写出解答过程,请把答案
直接填写在答题卷相应位置上)
如图,AD是△ABC的高,AE是△ABC的角平分线,若∠B=48°,
∠C=62°,则∠DAE的度数是 .
如图,在△ABC中,DE是AC的垂直平分线.若AE=3,△ABD的
周长为13,则△ABC的周长为 .
11题图
13.如图,已知:点P(2m+1,5m﹣2)在第一象限角平分线OC上,∠BPA=90°,角两边与x轴、y轴分别交于A点、B点,则OA+OB的值为 .
14.如图,将一副三角尺按图中所示位置摆放,点C在FD的延长线上,点C、F分别为直角顶点,且∠A=60°,∠E=45°,若AB∥CF,则∠CBD的度数是 ;
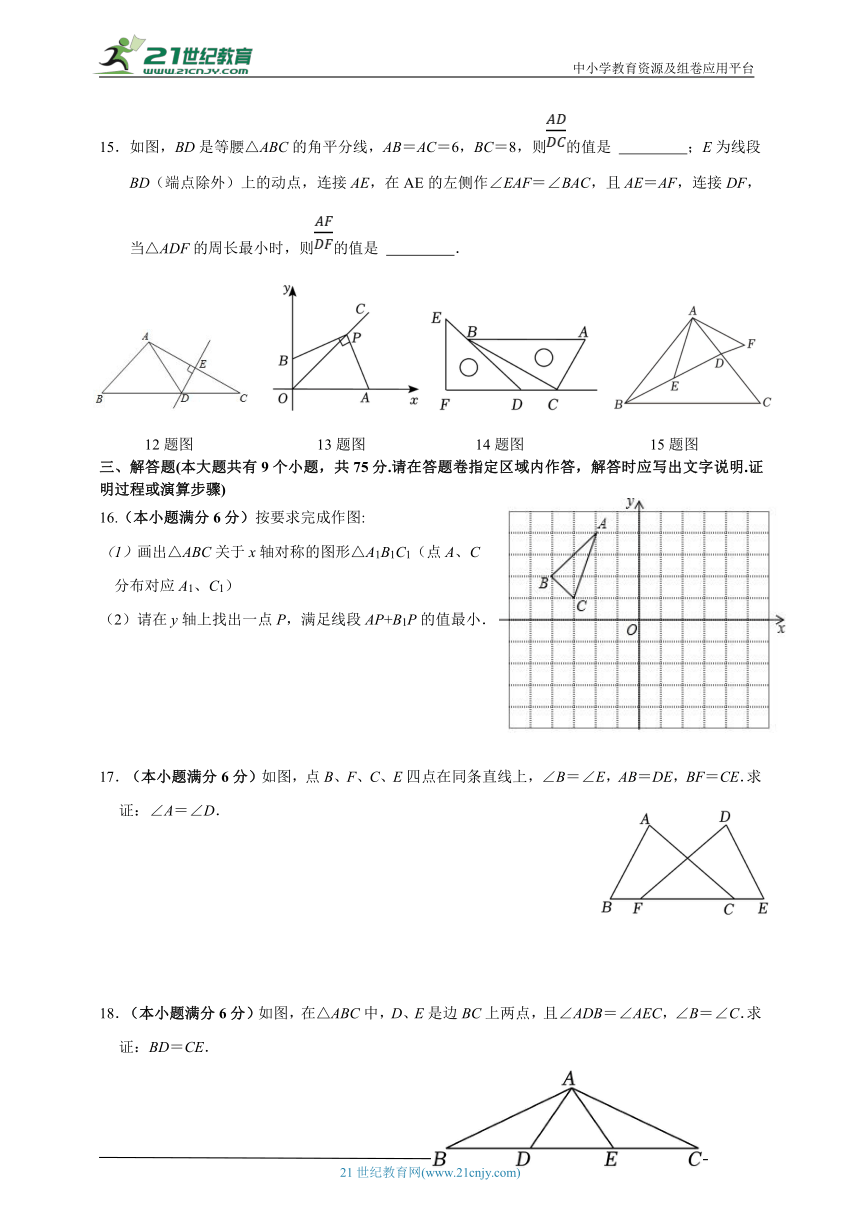
15.如图,BD是等腰△ABC的角平分线,AB=AC=6,BC=8,则的值是 ;E为线段BD(端点除外)上的动点,连接AE,在AE的左侧作∠EAF=∠BAC,且AE=AF,连接DF,当△ADF的周长最小时,则的值是 .
12题图 13题图 14题图 15题图
三、解答题(本大题共有9个小题,共75分.请在答题卷指定区域内作答,解答时应写出文字说明.证明过程或演算步骤)
16.(本小题满分6分)按要求完成作图:
画出△ABC关于x轴对称的图形△A1B1C1(点A、C
分布对应A1、C1)
(2)请在y轴上找出一点P,满足线段AP+B1P的值最小.
17.(本小题满分6分)如图,点B、F、C、E四点在同条直线上,∠B=∠E,AB=DE,BF=CE.求证:∠A=∠D.
18.(本小题满分6分)如图,在△ABC中,D、E是边BC上两点,且∠ADB=∠AEC,∠B=∠C.求证:BD=CE.
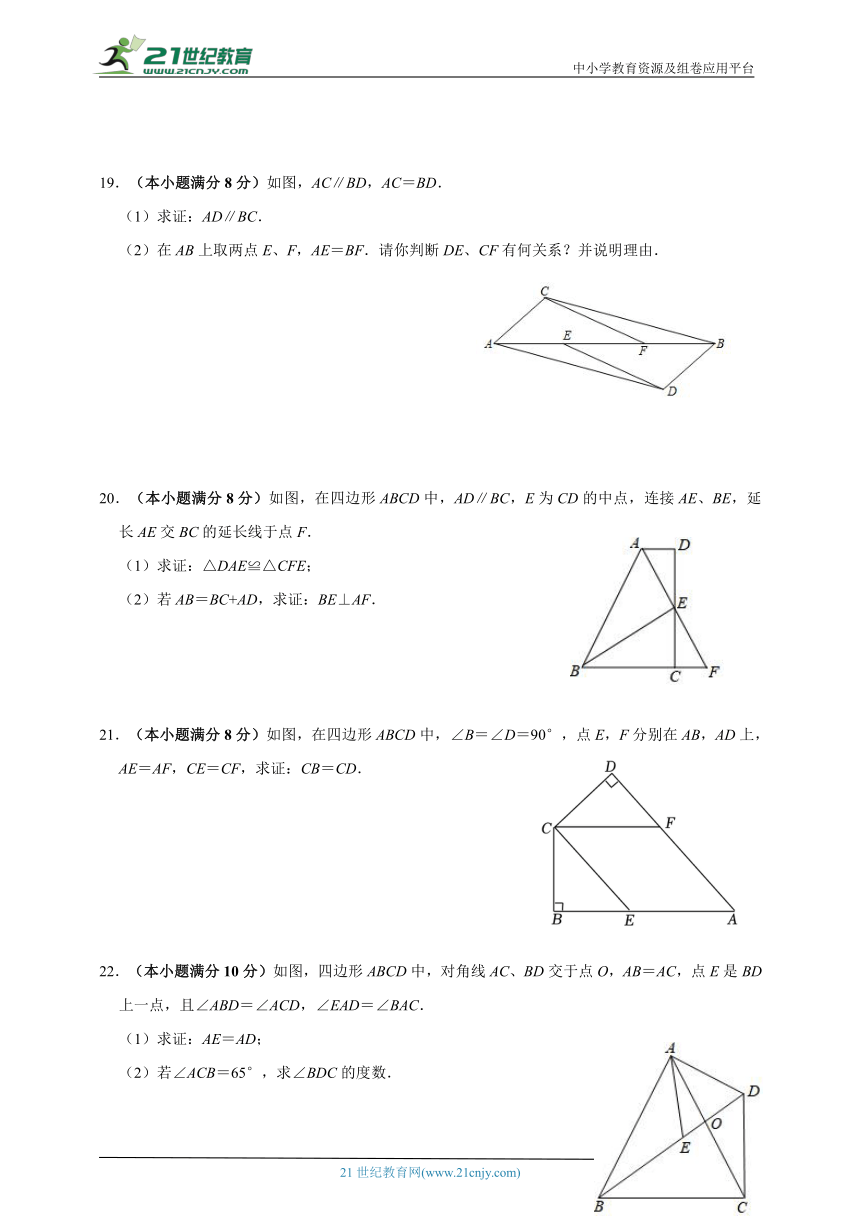
19.(本小题满分8分)如图,AC∥BD,AC=BD.
(1)求证:AD∥BC.
(2)在AB上取两点E、F,AE=BF.请你判断DE、CF有何关系?并说明理由.
20.(本小题满分8分)如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
(1)求证:△DAE≌△CFE;
(2)若AB=BC+AD,求证:BE⊥AF.
21.(本小题满分8分)如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,AE=AF,CE=CF,求证:CB=CD.
22.(本小题满分10分)如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且∠ABD=∠ACD,∠EAD=∠BAC.
(1)求证:AE=AD;
(2)若∠ACB=65°,求∠BDC的度数.
23.(本小题满分11分)如图,△ABC为等边三角形,AE=CD,AD交BE于点P,BQ⊥AD于Q.
(1)求证:AD=BE;
(2)若PQ=6,PE=2,求AD的长;
(3)连接PC,若BP⊥PC,求的值.
24.(本小题满分12分)在平面直角坐标系中,A(a,0),B(0,b)(a,b均为正数).
(1)若|a﹣3|+(b﹣4)2=0,直接写出A、B两点的坐标;
(2)如图1,在(1)的条件下,点C在x轴的负半轴上,AC=BC,点D在BC的延长线上,BA=AD,求CD+CO的值;
(3)如图2,在△BAN和△BOM中,BA=BN,BO=BM,∠ABN=∠OBM,射线MO交线段AN于点P.求证:点P为线段AN的中点.
2024年秋季学期八年级第一阶段学业评估数学试题参考答案
选择题
ADBAC BDADD
填空题
7° 12. 19 13. 6 14. 15° 15. ;
解答题
16.【解答】解:(1)如图所示:
(2)如图所示:点P即为所求.
17.【解答】证明:∵BF=CE,
∴BF+CF=CE+CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠A=∠D.
18.【解答】证明:∵∠B=∠C,
∴AB=AC,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(AAS),
∴BD=CE.
19.【解答】(1)证明:∵AC∥BD,
∴∠CAB=∠DBA,
在△ABC和△BAD中,
,
∴△ABC≌△BAD(SAS),
∴∠ABC=∠BAD,
∴AD∥BC;
(2)解:DE=CF且DE∥CF,理由如下:
由(1)知,△ABC≌△BAD,
∴BC=AD,∠FBC=∠EAD,
在△AED和△BFC中,
,
∴△AED≌△BFC(SAS),
∴DE=CF,∠AED=∠BFC,
∴180°﹣∠AED=180°﹣∠BFC,
即∠DEB=∠AFC,
∴DE∥CF,
∴DE=CF且DE∥CF.
20.【解答】证明:(1)△DAE≌△CFE理由如下:
∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
∵在△ADE与△FCE中,
,
∴△ADE≌△FCE(ASA);
(2)由(1)知△ADE≌△FCE,
∴AE=EF,AD=CF,
∵AB=BC+AD,
∴AB=BC+CF,
即AB=BF,在△ABE与△FBE中,
,
∴△ABE≌△FBE(SSS),
∴∠AEB=∠FEB=90°,
∴BE⊥AE;
21.【解答】证明:如图,连接AC,
在△ACE和△ACF中,
,
∴△ACE≌△ACF(SSS),
∴∠EAC=∠FAC,
∵∠B=∠D=90°,
∴CB=CD.
22.【解答】证明:(1)∵∠BAC=∠EAD
∴∠BAC﹣∠EAC=∠EAD﹣∠EAC
即:∠BAE=∠CAD
在△ABE和△ACD中
,
∴△ABE≌△ACD(ASA),
∴AE=AD;
(2)解:∵∠ACB=65°,AB=AC,
∴∠ABC=∠ACB=65°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣65°﹣65°=50°,
∵∠ABD=∠ACD,∠AOB=∠COD,
∴∠BDC=∠BAC=50°.
23.【解答】(1)证明:∵△ABC为等边三角形,
∴∠BAC=∠C=60°,AB=CA,
在△ABE和△CAD中
,
∴△ABE≌△CAD(SAS),
∴AD=BE;
(2)解:∵△ABE≌△CAD,
∴BE=AD,∠ABE=∠CAD,
∴∠ABE+∠BAP=∠CAD+∠BAP,
∴∠BPQ=∠BAC=60°,
∵BQ⊥AD,
∴∠BQP=90°,
∴∠PBQ=30°,
∴BP=2PQ=12,
∴AD=BE=BP+PE=14;
(3)如图所示:
∵∠ABE=∠CAD,
∴∠ABC﹣∠ABE=∠BAC﹣∠CAD,
∴∠PBC=∠BAQ,
在△ABQ和△CBP中
,
∴△ABQ≌△CBP(AAS),
∴AQ=BP=2PQ,
∴AP=PQ,
∴1.
24.【解答】(1)解:∵|a﹣3|+(b﹣4)2=0,
∴a﹣3=0,b﹣4=0,
∴a=3,b=4,
∴A (3,0 ),B(0,4);
(2)解:在x轴上取点M,使得CM=CD,连接BM,
在△BCM和△ACD中,
,
∴△BCM≌△ACD(SAS),
∴BM=AD=AB,
又∵BO⊥AO,
∴OA=OM,
∴CD+CO=CM+CO=MO=OA=3;
(3)证明:连接MN,过点N作NC∥OA交MP的延长线于点C,
设∠AOC=∠C=α,则∠BOM=90°﹣α,
∵∠ABN=∠OBM,
∴∠ABO=∠NBM,
∵AB=BN,OB=BM,
∴△BMN≌△BOA(SAS),
∴OA=MN,∠BMN=∠BOA=90°,
∵∠BMO=∠BOM=90°﹣α,
∴∠CMN=∠C=α,
∴MN=CN=OA,
∵CN∥OA,
∴∠C=∠AOC,∠OAP=∠CNP,
∴△OAP≌△CNP(ASA),
∴NP=AP.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2024年秋季学期八年级第一阶段学业评估数学试题
本试卷共6页,24 个小题,满分120分,考试用时120分钟
★祝考试顺利★
注意事项:
1.考生答题全部在答题卷上,答在试题卷上无效。
2.请认真核对监考教师在答题卷上所粘贴条形码的姓名、准考证号码是否与本人相符合,再将自己的姓名、准考证号码用0.5毫米的黑色墨水签字笔填写在答题卷及试题卷上。
3.选择题作答必须用2B铅笔将答题卷上对应的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案,非选择题作答必须用0.5毫米黑色墨水签字笔写在答题卷上指定位置,在其他位置答题一律无效。
4.作图必须用2B铅笔作答,并请加黑加粗,描写清楚。
5.考生不得折叠答题卷,保持答题卷的整洁.考试结束后,请将试题卷和答题卷一并上交。
一、选择题(本大题共有10个小题,每小题3分,共30分.在每小题给出的四个选项中,
只有一项是符合题目要求的,请将正确选择项前的字母代号填涂在答题卷相应位置上)
1.下列长度的三根小木棒,不能摆成三角形的是( )
A.6cm,6cm,13cm B.5cm,7cm,11cm C.9cm,6cm,8cm D.3cm,4cm,5cm
2.下列图形中是轴对称图形的是( )
A. B. C. D.
3.如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )
A.∠B=∠C B.BE=CD C.BD=CE D.∠ADC=∠AEB
4.如图,∠BAC=140°,若DM和EN分别垂直平分AB和AC,则∠DAE等于( )
A.100° B.90° C.80° D.70°
5.如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E,∠A=∠ABE,BD=1,BC=3,则AC的长为( )
A.4 B.4.5 C.5 D.5.5
3题图 4题图 5题图
6.某商店出售下列四种形状的地砖:①正三角形;②正方形;③正五边形;④正六边形.
若只选购其中一种地砖镶嵌地面,可供选择的地砖共有( )
A.4种 B.3种 C.2种 D.1种
7.如图,在△ABC中,AB=AC,∠A=36°,点D,P分别是图中所作直线和射线与AB,CD的交点.根据图中尺规作图的痕迹推断,以下结论错误的是( )
A.∠ABP=∠A B.AD=CD C.∠PBC=∠ACD D.∠BPC=118°
8.如图,将正五边形纸片ABCDE折叠,使点B与点E重合,折痕为AM,展开后,再将纸片折叠,使边AB落在线段AM上,点B的对应点为点B',折痕为AF,则∠AFB'=( )度.
A.45 B.36 C.54 D.48
9.如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为点N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则DE的长是( )
A.6 B.4 C.2 D.5
10.如图,△ABC中,AD⊥BC交BC于D,AE平分∠BAC交BC于E,F为BC的延长线上一点,FG⊥AE交AD的延长线于G,AC的延长线交FG于H,连接BG,下列结论:
①∠DAE=∠F; ②2∠DAE=∠ABD﹣∠ACE; ③S△AEB:S△AEC=AB:AC;
④∠AGH=∠BAE+∠ACB.其中正确的结论有( )个.
A.1 B.2 C.3 D.4
7题图 8题图 9题图 10题图
二、填空题(本大题共有5小题,每小题3分,共15分.不要求写出解答过程,请把答案
直接填写在答题卷相应位置上)
如图,AD是△ABC的高,AE是△ABC的角平分线,若∠B=48°,
∠C=62°,则∠DAE的度数是 .
如图,在△ABC中,DE是AC的垂直平分线.若AE=3,△ABD的
周长为13,则△ABC的周长为 .
11题图
13.如图,已知:点P(2m+1,5m﹣2)在第一象限角平分线OC上,∠BPA=90°,角两边与x轴、y轴分别交于A点、B点,则OA+OB的值为 .
14.如图,将一副三角尺按图中所示位置摆放,点C在FD的延长线上,点C、F分别为直角顶点,且∠A=60°,∠E=45°,若AB∥CF,则∠CBD的度数是 ;
15.如图,BD是等腰△ABC的角平分线,AB=AC=6,BC=8,则的值是 ;E为线段BD(端点除外)上的动点,连接AE,在AE的左侧作∠EAF=∠BAC,且AE=AF,连接DF,当△ADF的周长最小时,则的值是 .
12题图 13题图 14题图 15题图
三、解答题(本大题共有9个小题,共75分.请在答题卷指定区域内作答,解答时应写出文字说明.证明过程或演算步骤)
16.(本小题满分6分)按要求完成作图:
画出△ABC关于x轴对称的图形△A1B1C1(点A、C
分布对应A1、C1)
(2)请在y轴上找出一点P,满足线段AP+B1P的值最小.
17.(本小题满分6分)如图,点B、F、C、E四点在同条直线上,∠B=∠E,AB=DE,BF=CE.求证:∠A=∠D.
18.(本小题满分6分)如图,在△ABC中,D、E是边BC上两点,且∠ADB=∠AEC,∠B=∠C.求证:BD=CE.
19.(本小题满分8分)如图,AC∥BD,AC=BD.
(1)求证:AD∥BC.
(2)在AB上取两点E、F,AE=BF.请你判断DE、CF有何关系?并说明理由.
20.(本小题满分8分)如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
(1)求证:△DAE≌△CFE;
(2)若AB=BC+AD,求证:BE⊥AF.
21.(本小题满分8分)如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,AE=AF,CE=CF,求证:CB=CD.
22.(本小题满分10分)如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且∠ABD=∠ACD,∠EAD=∠BAC.
(1)求证:AE=AD;
(2)若∠ACB=65°,求∠BDC的度数.
23.(本小题满分11分)如图,△ABC为等边三角形,AE=CD,AD交BE于点P,BQ⊥AD于Q.
(1)求证:AD=BE;
(2)若PQ=6,PE=2,求AD的长;
(3)连接PC,若BP⊥PC,求的值.
24.(本小题满分12分)在平面直角坐标系中,A(a,0),B(0,b)(a,b均为正数).
(1)若|a﹣3|+(b﹣4)2=0,直接写出A、B两点的坐标;
(2)如图1,在(1)的条件下,点C在x轴的负半轴上,AC=BC,点D在BC的延长线上,BA=AD,求CD+CO的值;
(3)如图2,在△BAN和△BOM中,BA=BN,BO=BM,∠ABN=∠OBM,射线MO交线段AN于点P.求证:点P为线段AN的中点.
2024年秋季学期八年级第一阶段学业评估数学试题参考答案
选择题
ADBAC BDADD
填空题
7° 12. 19 13. 6 14. 15° 15. ;
解答题
16.【解答】解:(1)如图所示:
(2)如图所示:点P即为所求.
17.【解答】证明:∵BF=CE,
∴BF+CF=CE+CF,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠A=∠D.
18.【解答】证明:∵∠B=∠C,
∴AB=AC,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(AAS),
∴BD=CE.
19.【解答】(1)证明:∵AC∥BD,
∴∠CAB=∠DBA,
在△ABC和△BAD中,
,
∴△ABC≌△BAD(SAS),
∴∠ABC=∠BAD,
∴AD∥BC;
(2)解:DE=CF且DE∥CF,理由如下:
由(1)知,△ABC≌△BAD,
∴BC=AD,∠FBC=∠EAD,
在△AED和△BFC中,
,
∴△AED≌△BFC(SAS),
∴DE=CF,∠AED=∠BFC,
∴180°﹣∠AED=180°﹣∠BFC,
即∠DEB=∠AFC,
∴DE∥CF,
∴DE=CF且DE∥CF.
20.【解答】证明:(1)△DAE≌△CFE理由如下:
∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
∵在△ADE与△FCE中,
,
∴△ADE≌△FCE(ASA);
(2)由(1)知△ADE≌△FCE,
∴AE=EF,AD=CF,
∵AB=BC+AD,
∴AB=BC+CF,
即AB=BF,在△ABE与△FBE中,
,
∴△ABE≌△FBE(SSS),
∴∠AEB=∠FEB=90°,
∴BE⊥AE;
21.【解答】证明:如图,连接AC,
在△ACE和△ACF中,
,
∴△ACE≌△ACF(SSS),
∴∠EAC=∠FAC,
∵∠B=∠D=90°,
∴CB=CD.
22.【解答】证明:(1)∵∠BAC=∠EAD
∴∠BAC﹣∠EAC=∠EAD﹣∠EAC
即:∠BAE=∠CAD
在△ABE和△ACD中
,
∴△ABE≌△ACD(ASA),
∴AE=AD;
(2)解:∵∠ACB=65°,AB=AC,
∴∠ABC=∠ACB=65°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣65°﹣65°=50°,
∵∠ABD=∠ACD,∠AOB=∠COD,
∴∠BDC=∠BAC=50°.
23.【解答】(1)证明:∵△ABC为等边三角形,
∴∠BAC=∠C=60°,AB=CA,
在△ABE和△CAD中
,
∴△ABE≌△CAD(SAS),
∴AD=BE;
(2)解:∵△ABE≌△CAD,
∴BE=AD,∠ABE=∠CAD,
∴∠ABE+∠BAP=∠CAD+∠BAP,
∴∠BPQ=∠BAC=60°,
∵BQ⊥AD,
∴∠BQP=90°,
∴∠PBQ=30°,
∴BP=2PQ=12,
∴AD=BE=BP+PE=14;
(3)如图所示:
∵∠ABE=∠CAD,
∴∠ABC﹣∠ABE=∠BAC﹣∠CAD,
∴∠PBC=∠BAQ,
在△ABQ和△CBP中
,
∴△ABQ≌△CBP(AAS),
∴AQ=BP=2PQ,
∴AP=PQ,
∴1.
24.【解答】(1)解:∵|a﹣3|+(b﹣4)2=0,
∴a﹣3=0,b﹣4=0,
∴a=3,b=4,
∴A (3,0 ),B(0,4);
(2)解:在x轴上取点M,使得CM=CD,连接BM,
在△BCM和△ACD中,
,
∴△BCM≌△ACD(SAS),
∴BM=AD=AB,
又∵BO⊥AO,
∴OA=OM,
∴CD+CO=CM+CO=MO=OA=3;
(3)证明:连接MN,过点N作NC∥OA交MP的延长线于点C,
设∠AOC=∠C=α,则∠BOM=90°﹣α,
∵∠ABN=∠OBM,
∴∠ABO=∠NBM,
∵AB=BN,OB=BM,
∴△BMN≌△BOA(SAS),
∴OA=MN,∠BMN=∠BOA=90°,
∵∠BMO=∠BOM=90°﹣α,
∴∠CMN=∠C=α,
∴MN=CN=OA,
∵CN∥OA,
∴∠C=∠AOC,∠OAP=∠CNP,
∴△OAP≌△CNP(ASA),
∴NP=AP.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
