4.6.3余角和补角课时提升作业(含解析)
文档属性
| 名称 | 4.6.3余角和补角课时提升作业(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 68.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-30 13:52:17 | ||
图片预览

文档简介
4.6.3余角和补角课时提升作业(含解析)
一、选择题(每小题4分,共12分)
1.如果∠1和∠2互为余角,∠1与∠3互为补角,∠2与∠3的和等于120°,那么这三个角的度数分别是 ( )
A.75°,15°,105° B.30°,60°,120°
C.50°,40°,130° D.70°,20°,110°
【解析】选A.设∠1=x°,则∠2=(90-x)°,∠3=(180-x)°,
因为∠2与∠3的和等于120°,所以90-x+180-x=120,
解得x=75,所以∠1=75°,∠2=15°,∠3=105°.
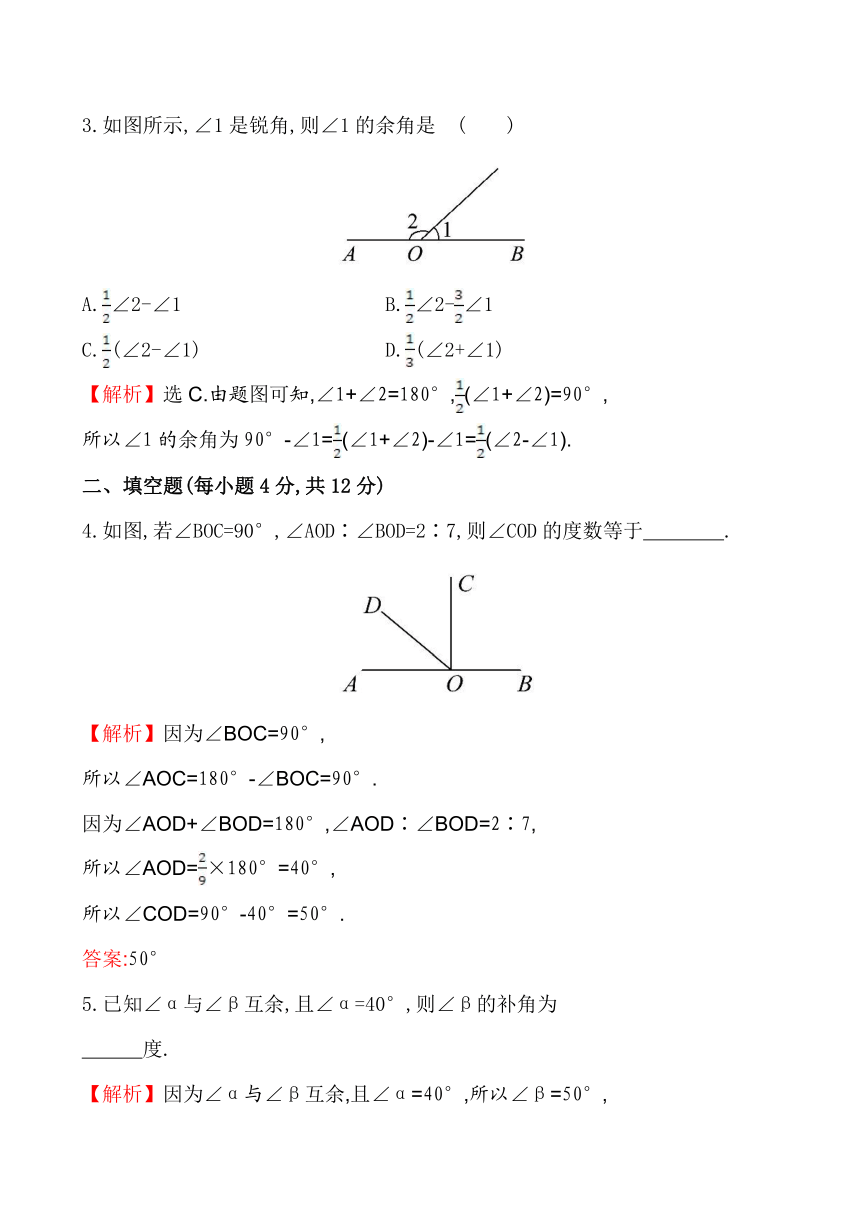
2.已知:如图,四边形ABCD为正方形,E为BC上的点,且AE⊥EF,则∠2与∠3的关系是 ( )
A.互余 B.互补 C.相等 D.不确定
【解析】选C.因为三角形的内角和为180°,
所以∠1+∠3+∠B=180°,
又∠B=90°,
所以∠1+∠3=90°,
又∠1+∠AEF+∠2=180°,∠AEF=90°,
所以∠1+∠2=90°,故∠2=∠3.
3.如图所示,∠1是锐角,则∠1的余角是 ( )
A.∠2-∠1 B.∠2-∠1
C.(∠2-∠1) D.(∠2+∠1)
【解析】选C.由题图可知,∠1+∠2=180°,(∠1+∠2)=90°,
所以∠1的余角为90°-∠1=(∠1+∠2)-∠1=(∠2-∠1).
二、填空题(每小题4分,共12分)
4.如图,若∠BOC=90°,∠AOD∶∠BOD=2∶7,则∠COD的度数等于 .
【解析】因为∠BOC=90°,
所以∠AOC=180°-∠BOC=90°.
因为∠AOD+∠BOD=180°,∠AOD∶∠BOD=2∶7,
所以∠AOD=×180°=40°,
所以∠COD=90°-40°=50°.
答案:50°
5.已知∠α与∠β互余,且∠α=40°,则∠β的补角为
度.
【解析】因为∠α与∠β互余,且∠α=40°,所以∠β=50°,
所以∠β的补角=180°-∠β=130°.
答案:130
【变式训练】若∠α的余角与∠α的补角的和是平角,则∠α= .
【解析】∠α的余角为90°-∠α,∠α的补角为180°-∠α,
所以(90°-∠α)+(180°-∠α)=180°,得∠α=45°.
答案:45°
6.如图,A,O,B三点在一条直线上,已知∠AOD=25°,∠COD=90°,则∠BOC的度数为 .
【解析】∠AOC=∠COD-∠AOD=90°-25°=65°,
∠BOC=∠AOB-∠AOC=180°-65°=115°.
答案:115°
三、解答题(共26分)
7.(8分)一个角的余角比这个角的补角的还小10°,求这个角的余角及这个角的补角.
【解析】设这个角为x°,则这个角的余角为(90-x)°,这个角的补角为
(180-x)°,根据题意,得90-x=(180-x)-10,解得x=60.则90-x=30,180-x=120.
答:这个角的余角是30°,补角是120°.
8.(8分)如图所示,点O在直线AD上,∠EOC=90°,∠DOB=90°.
(1)图中除∠EOC,∠DOB外,还有哪个角是直角
(2)图中哪两个锐角相等 并说明理由.
【解析】(1)因为AD是直线,∠DOB=90°,
所以∠AOB=90°.
(2)∠EOD=∠BOC.
理由:因为∠EOD+∠COD=90°,
∠BOC+∠COD=90°,
所以∠EOD=∠BOC.(同角的余角相等)
【培优训练】
9.(10分)按图所示的方法折纸,然后回答问题:
(1)∠2是多少度的角 为什么
(2)∠1与∠3有何关系
(3)∠1与∠AEC,∠3与∠BEF分别有何关系
【解析】(1)∠2=90°.因为折叠,则∠1与∠3的和与∠2相等,而这三个角加起来,正好是平角∠BEC,所以∠2=×180°=90°.
(2)因为∠1与∠3的和与∠2相等,且三个角加起来恰好是一个平角,所以∠1+∠3=90°,所以∠1与∠3互余.
(3)因为∠1与∠AEC的和为180°,∠3与∠BEF的和为180°,所以∠1与∠AEC互补,∠3与∠BEF互补.
一、选择题(每小题4分,共12分)
1.如果∠1和∠2互为余角,∠1与∠3互为补角,∠2与∠3的和等于120°,那么这三个角的度数分别是 ( )
A.75°,15°,105° B.30°,60°,120°
C.50°,40°,130° D.70°,20°,110°
【解析】选A.设∠1=x°,则∠2=(90-x)°,∠3=(180-x)°,
因为∠2与∠3的和等于120°,所以90-x+180-x=120,
解得x=75,所以∠1=75°,∠2=15°,∠3=105°.
2.已知:如图,四边形ABCD为正方形,E为BC上的点,且AE⊥EF,则∠2与∠3的关系是 ( )
A.互余 B.互补 C.相等 D.不确定
【解析】选C.因为三角形的内角和为180°,
所以∠1+∠3+∠B=180°,
又∠B=90°,
所以∠1+∠3=90°,
又∠1+∠AEF+∠2=180°,∠AEF=90°,
所以∠1+∠2=90°,故∠2=∠3.
3.如图所示,∠1是锐角,则∠1的余角是 ( )
A.∠2-∠1 B.∠2-∠1
C.(∠2-∠1) D.(∠2+∠1)
【解析】选C.由题图可知,∠1+∠2=180°,(∠1+∠2)=90°,
所以∠1的余角为90°-∠1=(∠1+∠2)-∠1=(∠2-∠1).
二、填空题(每小题4分,共12分)
4.如图,若∠BOC=90°,∠AOD∶∠BOD=2∶7,则∠COD的度数等于 .
【解析】因为∠BOC=90°,
所以∠AOC=180°-∠BOC=90°.
因为∠AOD+∠BOD=180°,∠AOD∶∠BOD=2∶7,
所以∠AOD=×180°=40°,
所以∠COD=90°-40°=50°.
答案:50°
5.已知∠α与∠β互余,且∠α=40°,则∠β的补角为
度.
【解析】因为∠α与∠β互余,且∠α=40°,所以∠β=50°,
所以∠β的补角=180°-∠β=130°.
答案:130
【变式训练】若∠α的余角与∠α的补角的和是平角,则∠α= .
【解析】∠α的余角为90°-∠α,∠α的补角为180°-∠α,
所以(90°-∠α)+(180°-∠α)=180°,得∠α=45°.
答案:45°
6.如图,A,O,B三点在一条直线上,已知∠AOD=25°,∠COD=90°,则∠BOC的度数为 .
【解析】∠AOC=∠COD-∠AOD=90°-25°=65°,
∠BOC=∠AOB-∠AOC=180°-65°=115°.
答案:115°
三、解答题(共26分)
7.(8分)一个角的余角比这个角的补角的还小10°,求这个角的余角及这个角的补角.
【解析】设这个角为x°,则这个角的余角为(90-x)°,这个角的补角为
(180-x)°,根据题意,得90-x=(180-x)-10,解得x=60.则90-x=30,180-x=120.
答:这个角的余角是30°,补角是120°.
8.(8分)如图所示,点O在直线AD上,∠EOC=90°,∠DOB=90°.
(1)图中除∠EOC,∠DOB外,还有哪个角是直角
(2)图中哪两个锐角相等 并说明理由.
【解析】(1)因为AD是直线,∠DOB=90°,
所以∠AOB=90°.
(2)∠EOD=∠BOC.
理由:因为∠EOD+∠COD=90°,
∠BOC+∠COD=90°,
所以∠EOD=∠BOC.(同角的余角相等)
【培优训练】
9.(10分)按图所示的方法折纸,然后回答问题:
(1)∠2是多少度的角 为什么
(2)∠1与∠3有何关系
(3)∠1与∠AEC,∠3与∠BEF分别有何关系
【解析】(1)∠2=90°.因为折叠,则∠1与∠3的和与∠2相等,而这三个角加起来,正好是平角∠BEC,所以∠2=×180°=90°.
(2)因为∠1与∠3的和与∠2相等,且三个角加起来恰好是一个平角,所以∠1+∠3=90°,所以∠1与∠3互余.
(3)因为∠1与∠AEC的和为180°,∠3与∠BEF的和为180°,所以∠1与∠AEC互补,∠3与∠BEF互补.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
