5.1.1对顶角课时提升作业(含解析)
文档属性
| 名称 | 5.1.1对顶角课时提升作业(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 89.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-30 13:52:58 | ||
图片预览


文档简介
5.1.1对顶角课时提升作业(含解析)
一、选择题(每小题4分,共12分)
1.下面各图中∠1与∠2是对顶角的是 ( )
【解题指南】解答本题的三个关键:
1.找相交直线.
2.两角有公共点.
3.角的两边互为反向延长线.
【解析】选B.观察四个选项,只有选项B中的∠1与∠2符合对顶角的定义;选项A和选项C中的两个角都不是两条直线相交所形成的角,它们没有公共顶点;选项D中的两个角是两条直线相交所形成的角,它们有公共顶点,但是有一条公共边,属于邻补角.
2.如图,已知∠1+∠3=180°,则图中和∠1互补的角有 ( )
A.1个 B.2个 C.3个 D.4个
【解析】选D.根据相加等于180°的两角称为互为补角,即两角互补.可知∠1的补角有它的两个邻补角∠5和∠7;另外∠1+∠3=180°,根据对顶角相等可知,
∠3=∠4,所以∠1+∠4=180°,即∠3和∠4也都是∠1的补角,所以和∠1互补的角有4个.
3.如图所示,直线AB与CD相交于O点,∠1=∠2.若∠AOE=140°,则∠AOC的度数为 ( )
A.40° B.60° C.80° D.100°
【解析】选C.因为∠AOE+∠2=180°,∠AOE=140°,所以∠2=180°-∠AOE=
180°-140°=40°.因为∠1=∠2,所以∠BOD=2∠2=80°.又因为∠AOC与∠BOD是对顶角,所以∠AOC=∠BOD=80°.
二、填空题(每小题4分,共12分)
4.如图,直线a,b相交于点O,若∠1=40°,则∠2= .
【解析】由图可知:∠1+∠2=180°,
因为∠1=40°,所以∠2=180°-40°=140°.
答案:140°
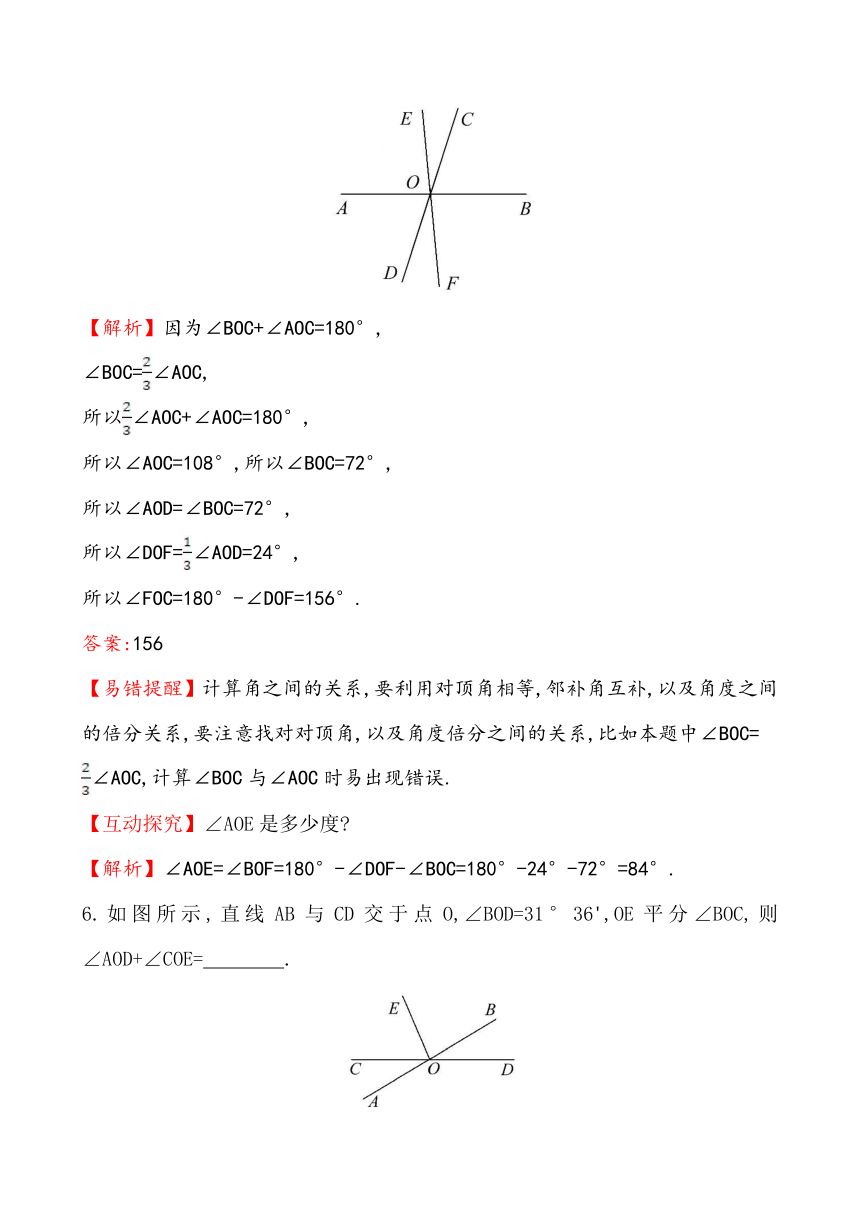
5.如图,直线AB,CD,EF相交于同一点O,且∠BOC=∠AOC,∠DOF=∠AOD,那么∠FOC= 度.
【解析】因为∠BOC+∠AOC=180°,
∠BOC=∠AOC,
所以∠AOC+∠AOC=180°,
所以∠AOC=108°,所以∠BOC=72°,
所以∠AOD=∠BOC=72°,
所以∠DOF=∠AOD=24°,
所以∠FOC=180°-∠DOF=156°.
答案:156
【易错提醒】计算角之间的关系,要利用对顶角相等,邻补角互补,以及角度之间的倍分关系,要注意找对对顶角,以及角度倍分之间的关系,比如本题中∠BOC=
∠AOC,计算∠BOC与∠AOC时易出现错误.
【互动探究】∠AOE是多少度
【解析】∠AOE=∠BOF=180°-∠DOF-∠BOC=180°-24°-72°=84°.
6.如图所示,直线AB与CD交于点O,∠BOD=31°36',OE平分∠BOC,则∠AOD+∠COE= .
【解析】因为∠BOD=31°36',∠BOC+∠BOD=180°,
所以∠AOD=∠BOC=148°24',
又因为OE是角平分线,所以∠COE=74°12',
所以∠AOD+∠COE=148°24'+74°12'=222°36'.
答案:222°36'
三、解答题(共26分)
7.(8分)如图,直线AB,CD相交于点O,OE平分∠AOC,∠COF=35°,∠BOD=60°,求∠EOF的度数.
【解析】因为∠BOD=60°,
所以∠AOC=60°(对顶角相等),
因为OE平分∠AOC,
所以∠AOE=∠EOC=∠AOC=30°,
所以∠EOF=∠EOC+∠COF=65°.
8.(8分)如图,直线AB,CD相交于点O,OE平分∠AOC,∠BOC-∠BOD=20°,求∠BOE的度数.
【解析】因为∠BOC-∠BOD=20°且∠BOC+∠BOD=180°,
所以∠BOC=100°,∠BOD=80°,所以∠AOC=80°,
因为OE平分∠AOC,
所以∠EOC=∠AOC=40°,
所以∠BOE=∠BOC+∠EOC=140°.
【培优训练】
9.(10分)观察下列图形,寻找对顶角(不含平角):
(1)两条直线相交(如图(1)),图中共有 对对顶角.
(2)三条直线相交于一点(如图(2)),图中共有 对对顶角.
(3)四条直线相交于一点(如图(3)),图中共有 对对顶角.
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可构成 对对顶角.
(5)若有2 014条直线相交于一点,则可构成 对对顶角.
【解题指南】解答本题的三点注意:
1.本题为规律探索题,注意每对数之间的关系.
2.由特殊到一般的数学方法.
3.两条直线相交于一点形成两对对顶角,三条直线相交于一点可以看成三种两条直线相交于一点的情况,四条直线相交于一点可看成是六种两条直线相交于一点的情况,依次类推.n条直线相交于一点可看成是种两条直线相交于一点的情况.
【解析】图(1)中有两条直线,共有2对对顶角,而2=2×1;图(2)中有三条直线,共有6对对顶角,而6=3×2;图(3)中有四条直线,共有12对对顶角,而12=4×3;……当有n条直线相交于一点时,共有n(n-1)对对顶角;若有2 014条直线相交于一点,则可构成2 014×2 013=4 054 182对对顶角.
答案:(1)2 (2)6 (3)12 (4)n(n-1)
(5)4 054 182
一、选择题(每小题4分,共12分)
1.下面各图中∠1与∠2是对顶角的是 ( )
【解题指南】解答本题的三个关键:
1.找相交直线.
2.两角有公共点.
3.角的两边互为反向延长线.
【解析】选B.观察四个选项,只有选项B中的∠1与∠2符合对顶角的定义;选项A和选项C中的两个角都不是两条直线相交所形成的角,它们没有公共顶点;选项D中的两个角是两条直线相交所形成的角,它们有公共顶点,但是有一条公共边,属于邻补角.
2.如图,已知∠1+∠3=180°,则图中和∠1互补的角有 ( )
A.1个 B.2个 C.3个 D.4个
【解析】选D.根据相加等于180°的两角称为互为补角,即两角互补.可知∠1的补角有它的两个邻补角∠5和∠7;另外∠1+∠3=180°,根据对顶角相等可知,
∠3=∠4,所以∠1+∠4=180°,即∠3和∠4也都是∠1的补角,所以和∠1互补的角有4个.
3.如图所示,直线AB与CD相交于O点,∠1=∠2.若∠AOE=140°,则∠AOC的度数为 ( )
A.40° B.60° C.80° D.100°
【解析】选C.因为∠AOE+∠2=180°,∠AOE=140°,所以∠2=180°-∠AOE=
180°-140°=40°.因为∠1=∠2,所以∠BOD=2∠2=80°.又因为∠AOC与∠BOD是对顶角,所以∠AOC=∠BOD=80°.
二、填空题(每小题4分,共12分)
4.如图,直线a,b相交于点O,若∠1=40°,则∠2= .
【解析】由图可知:∠1+∠2=180°,
因为∠1=40°,所以∠2=180°-40°=140°.
答案:140°
5.如图,直线AB,CD,EF相交于同一点O,且∠BOC=∠AOC,∠DOF=∠AOD,那么∠FOC= 度.
【解析】因为∠BOC+∠AOC=180°,
∠BOC=∠AOC,
所以∠AOC+∠AOC=180°,
所以∠AOC=108°,所以∠BOC=72°,
所以∠AOD=∠BOC=72°,
所以∠DOF=∠AOD=24°,
所以∠FOC=180°-∠DOF=156°.
答案:156
【易错提醒】计算角之间的关系,要利用对顶角相等,邻补角互补,以及角度之间的倍分关系,要注意找对对顶角,以及角度倍分之间的关系,比如本题中∠BOC=
∠AOC,计算∠BOC与∠AOC时易出现错误.
【互动探究】∠AOE是多少度
【解析】∠AOE=∠BOF=180°-∠DOF-∠BOC=180°-24°-72°=84°.
6.如图所示,直线AB与CD交于点O,∠BOD=31°36',OE平分∠BOC,则∠AOD+∠COE= .
【解析】因为∠BOD=31°36',∠BOC+∠BOD=180°,
所以∠AOD=∠BOC=148°24',
又因为OE是角平分线,所以∠COE=74°12',
所以∠AOD+∠COE=148°24'+74°12'=222°36'.
答案:222°36'
三、解答题(共26分)
7.(8分)如图,直线AB,CD相交于点O,OE平分∠AOC,∠COF=35°,∠BOD=60°,求∠EOF的度数.
【解析】因为∠BOD=60°,
所以∠AOC=60°(对顶角相等),
因为OE平分∠AOC,
所以∠AOE=∠EOC=∠AOC=30°,
所以∠EOF=∠EOC+∠COF=65°.
8.(8分)如图,直线AB,CD相交于点O,OE平分∠AOC,∠BOC-∠BOD=20°,求∠BOE的度数.
【解析】因为∠BOC-∠BOD=20°且∠BOC+∠BOD=180°,
所以∠BOC=100°,∠BOD=80°,所以∠AOC=80°,
因为OE平分∠AOC,
所以∠EOC=∠AOC=40°,
所以∠BOE=∠BOC+∠EOC=140°.
【培优训练】
9.(10分)观察下列图形,寻找对顶角(不含平角):
(1)两条直线相交(如图(1)),图中共有 对对顶角.
(2)三条直线相交于一点(如图(2)),图中共有 对对顶角.
(3)四条直线相交于一点(如图(3)),图中共有 对对顶角.
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可构成 对对顶角.
(5)若有2 014条直线相交于一点,则可构成 对对顶角.
【解题指南】解答本题的三点注意:
1.本题为规律探索题,注意每对数之间的关系.
2.由特殊到一般的数学方法.
3.两条直线相交于一点形成两对对顶角,三条直线相交于一点可以看成三种两条直线相交于一点的情况,四条直线相交于一点可看成是六种两条直线相交于一点的情况,依次类推.n条直线相交于一点可看成是种两条直线相交于一点的情况.
【解析】图(1)中有两条直线,共有2对对顶角,而2=2×1;图(2)中有三条直线,共有6对对顶角,而6=3×2;图(3)中有四条直线,共有12对对顶角,而12=4×3;……当有n条直线相交于一点时,共有n(n-1)对对顶角;若有2 014条直线相交于一点,则可构成2 014×2 013=4 054 182对对顶角.
答案:(1)2 (2)6 (3)12 (4)n(n-1)
(5)4 054 182
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
