5.1.3同位角、内错角、同旁内角课时提升作业(含解析)
文档属性
| 名称 | 5.1.3同位角、内错角、同旁内角课时提升作业(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 129.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-30 13:59:51 | ||
图片预览


文档简介
5.1.3同位角、内错角、同旁内角课时提升作业(含解析)
一、选择题(每小题4分,共12分)
1.如图,与∠1是同位角的是 ( )
A.∠2 B.∠3 C.∠4 D.∠5
【解析】选C.因为∠1与∠2是同旁内角,
所以选项A不符合题意;
因为∠1与∠3是内错角,
所以选项B不符合题意;
因为∠1与∠4是同位角,
所以选项C符合题意;
因为∠1与∠5无特殊位置关系,也不是同位角,
所以选项D不符合题意.
2.如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是
( )
A.同位角 B.内错角
C.对顶角 D.同旁内角
【解析】选B.角在被截线的内部,又在截线的两侧,符合内错角的定义.
【变式训练】如图,若直线MN与△ABC的边AB,AC分别交于点E,F,则图中的内错角有 ( )
A.2对 B.4对 C.6对 D.8对
【解析】选C.根据内错角定义,先找出两直线被第三条直线所截:MN,BC被AB所截得的∠MEB与∠ABC;被AC所截得的∠NFC与∠C;AC,MN被AB所截得的∠A与∠AEM;MN,AB被AC所截得∠A与∠AFN;AB,AC被MN所截得∠AEF与∠CFE,∠AFE与∠BEF.因此图中的内错角有6对.
3.如图所示,下列说法,正确的有 ( )
①∠1与∠2是同旁内角;
②∠1与∠ACE是内错角;
③∠B与∠4是同位角;
④∠1与∠3是内错角.
A.①③④ B.③④
C.①②④ D.①②③④
【解析】选D.①∠1与∠2是同旁内角,说法正确;
②∠1与∠ACE是内错角,说法正确;
③∠B与∠4是同位角,说法正确;
④∠1与∠3是内错角,说法正确.
【知识归纳】同位角、内错角、同旁内角的特征
(1)共同点:具有同位角、内错角、同旁内角的关系的一对角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截直线.
(2)不同点:同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形.
二、填空题(每小题4分,共12分)
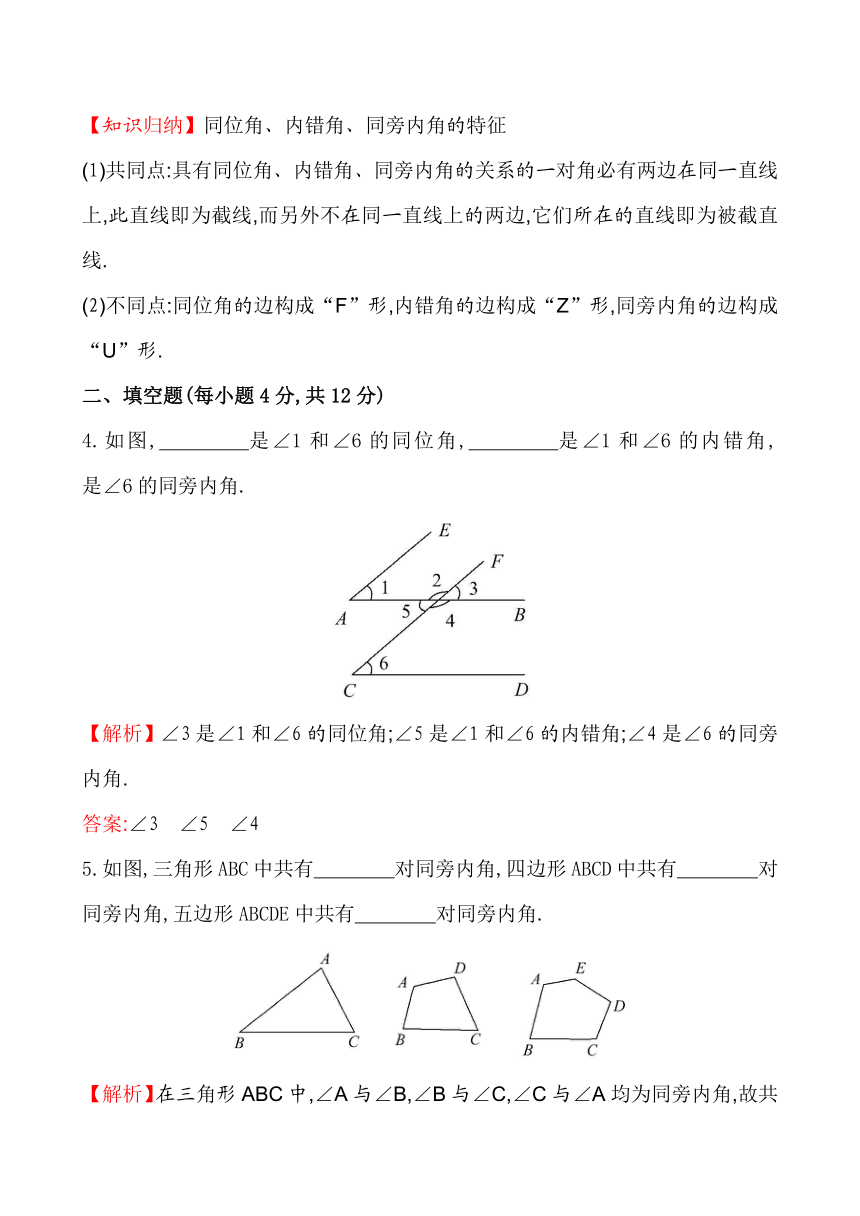
4.如图, 是∠1和∠6的同位角, 是∠1和∠6的内错角, 是∠6的同旁内角.
【解析】∠3是∠1和∠6的同位角;∠5是∠1和∠6的内错角;∠4是∠6的同旁内角.
答案:∠3 ∠5 ∠4
5.如图,三角形ABC中共有 对同旁内角,四边形ABCD中共有 对同旁内角,五边形ABCDE中共有 对同旁内角.
【解析】在三角形ABC中,∠A与∠B,∠B与∠C,∠C与∠A均为同旁内角,故共有3对.同理四边形ABCD,五边形ABCDE中共有4对和5对同旁内角.
答案:3 4 5
6.图中标有角号的角共有 对同位角, 对内错角, 对同旁内角.
【解题指南】
【解析】由图知,共有2对同位角:分别是∠7和∠1,∠5和∠6;4对内错角:分别是∠1和∠4,∠2和∠5,∠6和∠1,∠5和∠7;
4对同旁内角:分别是∠1和∠5,∠3和∠4,∠3和∠2,∠4和∠2.
答案:2 4 4
三、解答题(共26分)
7.(8分)如图所示,直线a,b被直线c所截,∠1=40°,∠2=105°,求∠1的同位角、∠4的内错角、∠3的同旁内角的度数.
【解题指南】本题涉及的两个关键:
1.找出相应的角:根据三类角的特征,准确地找出同位角、内错角、同旁内角.
2.计算:利用对顶角相等,邻补角互补进行角度计算.
【解析】∠1的同位角为∠4,而∠4+∠2=180°,因此∠4=180°-∠2=180°-
105°=75°;∠4的内错角与∠1的对顶角是同一个角,根据对顶角相等,∠4的内错角等于∠1=40°;∠3的同旁内角为∠4,因此∠3的同旁内角是75°.
8.(8分)如图,直线a,b被直线c所截,已知∠1=∠5,那么∠3与∠7的关系如何?请说明理由.
【解析】∠3=∠7.
因为∠1=∠3,∠5=∠7(对顶角相等),
又因为∠1=∠5(已知),
所以∠3=∠7(等量代换).
【互动探究】这8个角之间有怎样的关系?为什么?
【解析】由上题知,∠1=∠3=∠5=∠7,因为∠1+∠2=180°,∠3+∠4=180°,∠5+∠6=180°,∠7+∠8=180°,所以∠2=∠4=∠6=∠8,故两个角要么相等,要么互补.
【知识归纳】“三线八角”中角的关系
1.一般图形中,各对同位角、内错角、同旁内角只有位置关系,不存在数量关系.
2.在三线八角没有公共顶点的同位角、内错角、同旁内角中,当有一对角相等或互补时,其他各对角也相等或互补.
【培优训练】
9.(10分)如图,在平面中画一条直线,使得与∠A成同旁内角的角有3个,你能画出一条直线,使得与∠A成同旁内角的角最多吗?最多有几个?
【解析】如图(1),与∠A成同旁内角的角都有3个.
如图(2),与∠A成同旁内角的角最多,最多有4个.
一、选择题(每小题4分,共12分)
1.如图,与∠1是同位角的是 ( )
A.∠2 B.∠3 C.∠4 D.∠5
【解析】选C.因为∠1与∠2是同旁内角,
所以选项A不符合题意;
因为∠1与∠3是内错角,
所以选项B不符合题意;
因为∠1与∠4是同位角,
所以选项C符合题意;
因为∠1与∠5无特殊位置关系,也不是同位角,
所以选项D不符合题意.
2.如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是
( )
A.同位角 B.内错角
C.对顶角 D.同旁内角
【解析】选B.角在被截线的内部,又在截线的两侧,符合内错角的定义.
【变式训练】如图,若直线MN与△ABC的边AB,AC分别交于点E,F,则图中的内错角有 ( )
A.2对 B.4对 C.6对 D.8对
【解析】选C.根据内错角定义,先找出两直线被第三条直线所截:MN,BC被AB所截得的∠MEB与∠ABC;被AC所截得的∠NFC与∠C;AC,MN被AB所截得的∠A与∠AEM;MN,AB被AC所截得∠A与∠AFN;AB,AC被MN所截得∠AEF与∠CFE,∠AFE与∠BEF.因此图中的内错角有6对.
3.如图所示,下列说法,正确的有 ( )
①∠1与∠2是同旁内角;
②∠1与∠ACE是内错角;
③∠B与∠4是同位角;
④∠1与∠3是内错角.
A.①③④ B.③④
C.①②④ D.①②③④
【解析】选D.①∠1与∠2是同旁内角,说法正确;
②∠1与∠ACE是内错角,说法正确;
③∠B与∠4是同位角,说法正确;
④∠1与∠3是内错角,说法正确.
【知识归纳】同位角、内错角、同旁内角的特征
(1)共同点:具有同位角、内错角、同旁内角的关系的一对角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截直线.
(2)不同点:同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形.
二、填空题(每小题4分,共12分)
4.如图, 是∠1和∠6的同位角, 是∠1和∠6的内错角, 是∠6的同旁内角.
【解析】∠3是∠1和∠6的同位角;∠5是∠1和∠6的内错角;∠4是∠6的同旁内角.
答案:∠3 ∠5 ∠4
5.如图,三角形ABC中共有 对同旁内角,四边形ABCD中共有 对同旁内角,五边形ABCDE中共有 对同旁内角.
【解析】在三角形ABC中,∠A与∠B,∠B与∠C,∠C与∠A均为同旁内角,故共有3对.同理四边形ABCD,五边形ABCDE中共有4对和5对同旁内角.
答案:3 4 5
6.图中标有角号的角共有 对同位角, 对内错角, 对同旁内角.
【解题指南】
【解析】由图知,共有2对同位角:分别是∠7和∠1,∠5和∠6;4对内错角:分别是∠1和∠4,∠2和∠5,∠6和∠1,∠5和∠7;
4对同旁内角:分别是∠1和∠5,∠3和∠4,∠3和∠2,∠4和∠2.
答案:2 4 4
三、解答题(共26分)
7.(8分)如图所示,直线a,b被直线c所截,∠1=40°,∠2=105°,求∠1的同位角、∠4的内错角、∠3的同旁内角的度数.
【解题指南】本题涉及的两个关键:
1.找出相应的角:根据三类角的特征,准确地找出同位角、内错角、同旁内角.
2.计算:利用对顶角相等,邻补角互补进行角度计算.
【解析】∠1的同位角为∠4,而∠4+∠2=180°,因此∠4=180°-∠2=180°-
105°=75°;∠4的内错角与∠1的对顶角是同一个角,根据对顶角相等,∠4的内错角等于∠1=40°;∠3的同旁内角为∠4,因此∠3的同旁内角是75°.
8.(8分)如图,直线a,b被直线c所截,已知∠1=∠5,那么∠3与∠7的关系如何?请说明理由.
【解析】∠3=∠7.
因为∠1=∠3,∠5=∠7(对顶角相等),
又因为∠1=∠5(已知),
所以∠3=∠7(等量代换).
【互动探究】这8个角之间有怎样的关系?为什么?
【解析】由上题知,∠1=∠3=∠5=∠7,因为∠1+∠2=180°,∠3+∠4=180°,∠5+∠6=180°,∠7+∠8=180°,所以∠2=∠4=∠6=∠8,故两个角要么相等,要么互补.
【知识归纳】“三线八角”中角的关系
1.一般图形中,各对同位角、内错角、同旁内角只有位置关系,不存在数量关系.
2.在三线八角没有公共顶点的同位角、内错角、同旁内角中,当有一对角相等或互补时,其他各对角也相等或互补.
【培优训练】
9.(10分)如图,在平面中画一条直线,使得与∠A成同旁内角的角有3个,你能画出一条直线,使得与∠A成同旁内角的角最多吗?最多有几个?
【解析】如图(1),与∠A成同旁内角的角都有3个.
如图(2),与∠A成同旁内角的角最多,最多有4个.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
