6.1 圆周运动 学案(含解析)--高中物理人教版(2019)必修 第二册
文档属性
| 名称 | 6.1 圆周运动 学案(含解析)--高中物理人教版(2019)必修 第二册 |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-12-07 10:02:53 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
高中物理必修二素养提升学案
第六章 圆周运动
6.1 圆周运动
【课标解读】
1.认识圆周运动、匀速圆周运动的特点。了解转速和周期的意义。
2.理解线速度的物理意义,知道匀速圆周运动中线速度的方向。
3.理解角速度的物理意义,掌握线速度和角速度的关系。
【学科素养】
一.知识与技能
1.理解匀速圆周运动的特点,能举例说明生活中的圆周运动;
2.理解线速度、角速度和周期的物理意义,正确表述其定义式和关系式;
3.能够运用相关公式分析解决三种传动装置问题。
二.过程与方法
1.通过对生活中发生的圆周运动的观察,提高学生对事物变化的分析和概括能力;
2.经历圆周运动探究的过程,体验科学探究的思维方法,培养学生对新知识的探索的能力。
3.情感态度与价值观
1.在解决匀速圆周运动快慢问题时,体会一种运动可以从多个不同的方面分析研究,理解事物的多面性,学会事物之间普遍联系的思维。
2.通过学生间对于生活中的圆周运动现象的讨论与思考,培养学生独立思考的能力,同时加强团结互助能力。
3.培养学生应用所学公式去分析解决生活中的三种传动装置问题,逐步培养对于科学研究的兴趣和对生活的关注。
【思维脉络】
【课前预习】
知识点 1 线速度
1.圆周运动:运动轨迹为__圆周__或一段__圆弧__的机械运动。
2.线速度
(1)定义:物体运动的__弧长Δs__与时间Δt之比。
(2)定义式:v=____。
(3)方向:物体做圆周运动时该点的__切线__方向。
(4)物理意义:表示物体在该点运动的__快慢__。
3.匀速圆周运动:线速度__大小__处处相等的圆周运动。因线速度的方向在时刻变化,故匀速圆周运动是一种__变速__运动。
知识点 2 角速度
1.物理意义:描述做圆周运动的物体绕圆心__转动__的快慢。
2.定义:半径转过的__角度Δθ__与所用时间Δt之比。
3.定义式:ω=。
4.单位:在国际单位制中,角速度的单位是__弧度每秒__,符号:__rad/s__。
5.匀速圆周运动角速度特点:角速度__不变__。
知识点 3 周期
1.周期
(1)定义:做匀速圆周运动的物体,运动__一周__所用的时间。
(2)符号:用T表示。
(3)单位:国际单位制中,周期的单位是__秒__,符号:__s__。
2.转速
(1)物理意义:描述物体做圆周运动的__快慢__。
(2)定义:物体转动的__圈数__与所用时间之比。
(3)符号:用n表示。
(4)单位:转每秒(r/s),或转每分(r/min)。
知识点 4 线速度与角速度的关系
(1)关系推导:由v=,ω=,Δθ=,可得:v=__ωr__。
(2)在圆周运动中,线速度的大小等于角速度的大小与半径的__乘积__。
【思考辨析】
1、判断下列说法是否正确。
(1)做匀速圆周运动的物体,相同时间内位移相同。(×)
(2)做匀速圆周运动的物体,其线速度大小不变。(√)
(3)匀速圆周运动是一种匀速运动。(×)
(4)做匀速圆周运动的物体,其所受合力一定不为零。(√)
(5)做匀速圆周运动的物体,其角速度不变。(√)
(6)做匀速圆周运动的物体,周期越大,角速度越小。(√)
2. 以下物体的运动为匀变速曲线运动的是( C )
A.水平面内的匀速圆周运动
B.竖直面内的匀速圆周运动
C.平抛物体的运动
D.如图所示的圆锥摆运动
解析:匀变速曲线运动是加速度恒定的曲线运动。水平面内的匀速圆周运动,竖直面内的匀速圆周运动和如图所示的圆锥摆运动的加速度方向在变,即加速度不恒定;平抛物体的运动加速度为重力加速度g恒定,即为匀变速曲线运动,A、B、D错误,C正确。
3. 拍苍蝇与物理有关。市场上出售的蝇拍(如图所示)把长约30 cm,拍头长12 cm、宽10 cm,这种拍的使用效果往往不好,拍未到,蝇已飞。有人将拍把增长到60 cm,结果是打一个准一个,你能解释其原因吗?
答案:苍蝇的反应很灵敏,只有拍头的速度足够大时才能击中,而人转动手腕的角速度是有限的。由v=ωr知,当增大转动半径(即拍把长)时,如由30 cm增大到60 cm,则拍头速度增大为原来的2倍,此时,苍蝇就难以逃生了。
【互动探究】
探究一? 描述圆周运动的物理量及其关系
【情境导入】
月球绕地球运动,地球绕太阳运动,这两个运动都可看成是圆周运动,怎样比较这两个圆周运动的快慢?请看下面地球和月球的“对话”。
地球说:你怎么走得这么慢?我绕太阳运动1 s要走29.79 km,你绕我运动1 s才走1.02 km。
月球说:不能这样说吧!你一年才绕太阳转一圈,我27.3天就能绕你转一圈,到底谁转得慢?请问:地球说得对,还是月球说得对?
提示:地球和月球说的均是片面的,它们选择描述圆周运动快慢的标准不同。严格来说地球绕太阳运动的线速度比月球绕地球运动的线速度大,而月球绕地球转动的角速度比地球绕太阳转动的角度速度大。
【要点提炼】
1.匀速圆周运动的特点
(1)“变”与“不变”
描述匀速圆周运动的四个物理量中,角速度、周期和转速恒定不变,线速度是变化的。
(2)性质
匀速圆周运动中的“匀速”不同于匀速直线运动中的“匀速”,这里的“匀速”是“匀速率”的意思,匀速圆周运动是变速运动。
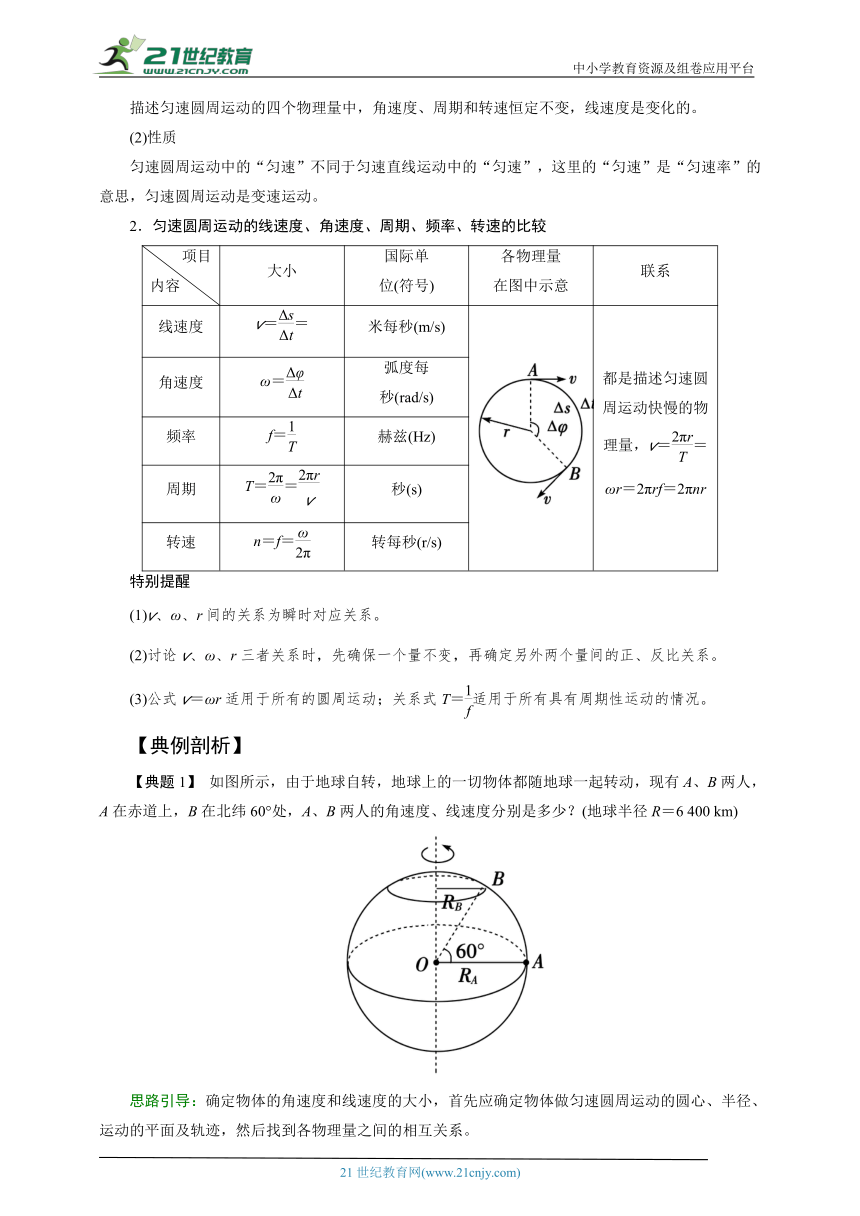
2.匀速圆周运动的线速度、角速度、周期、频率、转速的比较
项目内容 大小 国际单位(符号) 各物理量在图中示意 联系
线速度 v== 米每秒(m/s) 都是描述匀速圆周运动快慢的物理量,v==ωr=2πrf=2πnr
角速度 ω= 弧度每秒(rad/s)
频率 f= 赫兹(Hz)
周期 T== 秒(s)
转速 n=f= 转每秒(r/s)
特别提醒
(1)v、ω、r间的关系为瞬时对应关系。
(2)讨论v、ω、r三者关系时,先确保一个量不变,再确定另外两个量间的正、反比关系。
(3)公式v=ωr适用于所有的圆周运动;关系式T=适用于所有具有周期性运动的情况。
【典例剖析】
【典题1】 如图所示,由于地球自转,地球上的一切物体都随地球一起转动,现有A、B两人,A在赤道上,B在北纬60°处,A、B两人的角速度、线速度分别是多少?(地球半径R=6 400 km)
思路引导:确定物体的角速度和线速度的大小,首先应确定物体做匀速圆周运动的圆心、半径、运动的平面及轨迹,然后找到各物理量之间的相互关系。
解析:A、B两人随地球自转,做圆周运动的周期相同,均等于地球自转的周期,但两人做圆周运动的圆周、圆心的位置及轨道半径不同。
A、B两人的角速度相等,均等于地球的自转角速度。
ωA=ωB== rad/s=7.3×10-5 rad/s
由v=rω得
vA=RAωA=RωA=6.4×106×7.3×10-5m/s=467.2 m/s
vB= RBωB=Rcos 60°ωB=6.4×106×cos 60°×7.3×10-5m/s=233.6 m/s。
答案:ωA=ωB=7.3×10-5rad/s vA=467.2 m/s vB=233.6 m/s
【对点训练】
1.(2021·北京师范大学珠海分校高一月考)观察钟表指针转动情况,回答下列问题
(1)某教室用钟秒针针尖到转轴距离20 cm,求秒针针尖转动的角速度和线速度;
(2)若分针与时针由转轴到针尖的长度之比为2︰1,求分针与时针的角速度之比;
(3)求分针针尖与时针针尖线速度之比。
答案:(1)rad/s, m/s (2)12︰1 (3)24︰1
解析:(1)秒针转动周期为T=60 s,秒针针尖转动的角速度为ω==rad/s,
线速度为v=rω= m/s。
(2)分针转动周期为T1=1 h,时针转动周期为T2=12 h,由ω=可得,角速度与周期成反比,故分针与时针的角速度之比12︰1。
(3)由v=rω可得,分针、时针的线速度之比为=·=×=24。
探究二? 常见的三种传动装置及其特点
【情境导入】
如图为一辆自行车传动装置的结构图,观察自行车是怎样用链条传动来驱动后轮前进的,请思考:
(1)同一齿轮上到转轴距离不同的各点的线速度、角速度是否相同?
(2)两个齿轮相比较,其边缘的线速度大小是否相等?角速度是否相同,转速是否相同?
提示:(1)线速度不同,角速度相同。
(2)线速度大小相等,角速度不同,转速不同。
【要点提炼】
三种传动装置及其特点
同轴传动 皮带传动 齿轮传动
装置 A、B两点在同轴的一个圆盘上 两个轮子用皮带连接,A、B两点分别是两个轮子边缘的点 两个齿轮轮齿啮合,A、B两点s分别是两个齿轮边缘上的点
特点 角速度、周期相同 线速度大小相同 线速度大小相同
转动方向 相同 相同 相反
规律 线速度与半径成正比:= 角速度与半径成反比:=。周期与半径成正比:= 角速度与半径成反比:=。周期与半径成正比:=
特别提醒
在处理传动装置中各物理量间的关系时,关键是确定其相同的量(线速度或角速度),再由描述圆周运动的各物理量间的关系,确定其他各量间的关系。
【典例剖析】
【典题2】 (多选)(2021·四川南充市阆中市川绵外国语学校高一月考)如图所示皮带传送装置,皮带轮O和O′上的三点A、B和C,OA=O′C=r,O′B=2r。则皮带轮转动时A、B、C三点的情况是( AC )
A.vA=vB vB=2vC B.ωA=ωB vB=2vC
C.ωA=2ωB vA=2vC D.ωA=2ωB vA=vC
思路引导:在分析传动装置中各物理量间的关系时,要牢记下面的两个关系:(1)靠皮带、齿轮或摩擦传动的轮子,在不打滑的情况下,轮子边缘上各点的线速度大小相等,角速度则与半径成反比;(2)同一轮子或同轴传动的轮子上各点运动的角速度ω、转速n和周期T均相等,线速度则与半径成正比。
解析:由图可知B点和C点属于同轴传动,所以ωB=ωC,又rB=2rC,根据v=ωr,可知vB=2vC,A、B两点属于皮带传动,所以vA=vB,所以vA=2vC,又rB=2 rA,根据v=ωr,可知ωA=2ωB。故选AC。
【对点训练】
2.(多选)如图所示为一种齿轮传动装置,忽略齿轮啮合部分的厚度,甲、乙两个轮子的半径之比为1︰3,则在传动的过程中( AD )
A.甲、乙两轮的角速度之比为3︰1
B.甲、乙两轮的周期之比为3︰1
C.甲、乙两轮边缘处的线速度之比为3︰1
D.甲、乙两轮边缘上的点相等时间内转过的弧长之比为1︰1
解析:这种齿轮传动,与不打滑的皮带传动规律相同,即两轮边缘的线速度大小相等,故C错误;根据线速度的定义v=可知,弧长Δs=vΔt,故D正确;根据v=ωr可知ω=,又甲、乙两个轮子的半径之比r1︰r2=1︰3,故甲、乙两轮的角速度之比ω1︰ω2=r2︰r1=3︰1,故A正确;周期T=,所以甲、乙两轮的周期之比T1︰T2=ω2︰ω1=1︰3,故B错误。
【易错辨析】
易错点:忽视匀速圆周运动的周期性而致错
【典例】 如图所示,用薄纸做成的圆筒,直径为D,水平放置,绕圆筒轴线OO′以角速度ω0逆时针匀速转动。一玩具手枪发出的子弹,沿水平方向匀速飞来(不计子弹重力影响),沿圆筒的直径方向击穿圆筒后飞出(设薄纸对子弹的运动速度无影响且认为纸筒没有发生形变),结果在圆筒上只留下子弹的一个洞痕,求子弹的速度。
易错分析:认为圆筒只转过π弧度,根据t=,v=得子弹速度v=,这是忽视匀速圆周运动的周期性导致的错误。
正确解答:由于子弹在圆筒上只留下了一个洞痕,考虑匀速圆周运动的周期性,故有π+2nπ=ω0t(n=0,1,2,3,…)
解得t=(n=0,1,2,3,…)
所以v==(n=0,1,2,3,…)。
答案:(n=0,1,2,3,…)
名师点评:子弹穿过圆筒,只留下一个洞痕,圆筒转过的圈数必然为的奇数倍,明确这一点是列出“通式”的关键。本题的解题思路是分别研究两个运动对象,寻找相关量,不要让两个物体的运动互相干扰,导致出现解题失误。
素养警示
解答有关圆周运动的问题时,常出现的错误是没有考虑到圆周运动的周期性而漏解。因此,在解答此类问题时,要特别注意可能会出现的符合题意的多种情况。
【课堂达标检测】
1.(2021·四川南充市阆中市川绵外国语学校高一月考)关于圆周运动,下列说法中正确的是( C )
A.圆周运动可能是匀速运动
B.圆周运动可能是匀变速曲线运动
C.圆周运动一定是非匀变速运动
D.圆周运动加速度可能不变
解析:圆周运动是曲线运动,因此合外力不等于零。圆周运动的加速度方向是在变化的,所以圆周运动一定是非匀变速运动。故选C。
2.(2021·天津市第八中学高一月考)一户外健身器材如图所示,当器材上轮子转动时,轮子上A、B两点的( C )
A.转速nB>nA B.周期TB>TA
C.线速度vB>vA D.角速度ωB>ωA
解析:由于同轴转动,轮上各个点的角速度相同(圆心除外),所以A、B两点的角速度相同,转速相同,周期相同,ABD错误;由v=ωr,线速度vB>vA,C正确。
3.(2021·浙江高一月考)走时准确的时钟,时针和分针的角速度之比( A )
A.1︰12 B.12︰1
C.1︰60 D.60︰1
解析:时针转一圈需要12个小时,分针转一圈需要1小时,故其角速度之比为ω时:ω分=︰=1︰12,故选A。
4.(多选)(2021·江苏扬州市扬州中学高一月考)如图所示为某一皮带传动装置,主动轮的半径为r1,从动轮的半径为r2,已知主动轮做顺时针转动,转速为n,转动过程中皮带不打滑。下列说法正确的是( BC )
A.从动轮做顺时针转动
B.从动轮做逆时针转动
C.从动轮的转速为n
D.从动轮的转速为n
解析:主动轮做顺时针转动,由皮带缠绕的方式知从动轮做逆时针转动,B正确,A错误;两轮边缘的线速度大小相等,由v=rω,ω=2πn可知,2πn·r1=2πn′·r2,解得从动轮的转速n′=n,C正确,D错误。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
高中物理必修二素养提升学案
第六章 圆周运动
6.1 圆周运动
【课标解读】
1.认识圆周运动、匀速圆周运动的特点。了解转速和周期的意义。
2.理解线速度的物理意义,知道匀速圆周运动中线速度的方向。
3.理解角速度的物理意义,掌握线速度和角速度的关系。
【学科素养】
一.知识与技能
1.理解匀速圆周运动的特点,能举例说明生活中的圆周运动;
2.理解线速度、角速度和周期的物理意义,正确表述其定义式和关系式;
3.能够运用相关公式分析解决三种传动装置问题。
二.过程与方法
1.通过对生活中发生的圆周运动的观察,提高学生对事物变化的分析和概括能力;
2.经历圆周运动探究的过程,体验科学探究的思维方法,培养学生对新知识的探索的能力。
3.情感态度与价值观
1.在解决匀速圆周运动快慢问题时,体会一种运动可以从多个不同的方面分析研究,理解事物的多面性,学会事物之间普遍联系的思维。
2.通过学生间对于生活中的圆周运动现象的讨论与思考,培养学生独立思考的能力,同时加强团结互助能力。
3.培养学生应用所学公式去分析解决生活中的三种传动装置问题,逐步培养对于科学研究的兴趣和对生活的关注。
【思维脉络】
【课前预习】
知识点 1 线速度
1.圆周运动:运动轨迹为__圆周__或一段__圆弧__的机械运动。
2.线速度
(1)定义:物体运动的__弧长Δs__与时间Δt之比。
(2)定义式:v=____。
(3)方向:物体做圆周运动时该点的__切线__方向。
(4)物理意义:表示物体在该点运动的__快慢__。
3.匀速圆周运动:线速度__大小__处处相等的圆周运动。因线速度的方向在时刻变化,故匀速圆周运动是一种__变速__运动。
知识点 2 角速度
1.物理意义:描述做圆周运动的物体绕圆心__转动__的快慢。
2.定义:半径转过的__角度Δθ__与所用时间Δt之比。
3.定义式:ω=。
4.单位:在国际单位制中,角速度的单位是__弧度每秒__,符号:__rad/s__。
5.匀速圆周运动角速度特点:角速度__不变__。
知识点 3 周期
1.周期
(1)定义:做匀速圆周运动的物体,运动__一周__所用的时间。
(2)符号:用T表示。
(3)单位:国际单位制中,周期的单位是__秒__,符号:__s__。
2.转速
(1)物理意义:描述物体做圆周运动的__快慢__。
(2)定义:物体转动的__圈数__与所用时间之比。
(3)符号:用n表示。
(4)单位:转每秒(r/s),或转每分(r/min)。
知识点 4 线速度与角速度的关系
(1)关系推导:由v=,ω=,Δθ=,可得:v=__ωr__。
(2)在圆周运动中,线速度的大小等于角速度的大小与半径的__乘积__。
【思考辨析】
1、判断下列说法是否正确。
(1)做匀速圆周运动的物体,相同时间内位移相同。(×)
(2)做匀速圆周运动的物体,其线速度大小不变。(√)
(3)匀速圆周运动是一种匀速运动。(×)
(4)做匀速圆周运动的物体,其所受合力一定不为零。(√)
(5)做匀速圆周运动的物体,其角速度不变。(√)
(6)做匀速圆周运动的物体,周期越大,角速度越小。(√)
2. 以下物体的运动为匀变速曲线运动的是( C )
A.水平面内的匀速圆周运动
B.竖直面内的匀速圆周运动
C.平抛物体的运动
D.如图所示的圆锥摆运动
解析:匀变速曲线运动是加速度恒定的曲线运动。水平面内的匀速圆周运动,竖直面内的匀速圆周运动和如图所示的圆锥摆运动的加速度方向在变,即加速度不恒定;平抛物体的运动加速度为重力加速度g恒定,即为匀变速曲线运动,A、B、D错误,C正确。
3. 拍苍蝇与物理有关。市场上出售的蝇拍(如图所示)把长约30 cm,拍头长12 cm、宽10 cm,这种拍的使用效果往往不好,拍未到,蝇已飞。有人将拍把增长到60 cm,结果是打一个准一个,你能解释其原因吗?
答案:苍蝇的反应很灵敏,只有拍头的速度足够大时才能击中,而人转动手腕的角速度是有限的。由v=ωr知,当增大转动半径(即拍把长)时,如由30 cm增大到60 cm,则拍头速度增大为原来的2倍,此时,苍蝇就难以逃生了。
【互动探究】
探究一? 描述圆周运动的物理量及其关系
【情境导入】
月球绕地球运动,地球绕太阳运动,这两个运动都可看成是圆周运动,怎样比较这两个圆周运动的快慢?请看下面地球和月球的“对话”。
地球说:你怎么走得这么慢?我绕太阳运动1 s要走29.79 km,你绕我运动1 s才走1.02 km。
月球说:不能这样说吧!你一年才绕太阳转一圈,我27.3天就能绕你转一圈,到底谁转得慢?请问:地球说得对,还是月球说得对?
提示:地球和月球说的均是片面的,它们选择描述圆周运动快慢的标准不同。严格来说地球绕太阳运动的线速度比月球绕地球运动的线速度大,而月球绕地球转动的角速度比地球绕太阳转动的角度速度大。
【要点提炼】
1.匀速圆周运动的特点
(1)“变”与“不变”
描述匀速圆周运动的四个物理量中,角速度、周期和转速恒定不变,线速度是变化的。
(2)性质
匀速圆周运动中的“匀速”不同于匀速直线运动中的“匀速”,这里的“匀速”是“匀速率”的意思,匀速圆周运动是变速运动。
2.匀速圆周运动的线速度、角速度、周期、频率、转速的比较
项目内容 大小 国际单位(符号) 各物理量在图中示意 联系
线速度 v== 米每秒(m/s) 都是描述匀速圆周运动快慢的物理量,v==ωr=2πrf=2πnr
角速度 ω= 弧度每秒(rad/s)
频率 f= 赫兹(Hz)
周期 T== 秒(s)
转速 n=f= 转每秒(r/s)
特别提醒
(1)v、ω、r间的关系为瞬时对应关系。
(2)讨论v、ω、r三者关系时,先确保一个量不变,再确定另外两个量间的正、反比关系。
(3)公式v=ωr适用于所有的圆周运动;关系式T=适用于所有具有周期性运动的情况。
【典例剖析】
【典题1】 如图所示,由于地球自转,地球上的一切物体都随地球一起转动,现有A、B两人,A在赤道上,B在北纬60°处,A、B两人的角速度、线速度分别是多少?(地球半径R=6 400 km)
思路引导:确定物体的角速度和线速度的大小,首先应确定物体做匀速圆周运动的圆心、半径、运动的平面及轨迹,然后找到各物理量之间的相互关系。
解析:A、B两人随地球自转,做圆周运动的周期相同,均等于地球自转的周期,但两人做圆周运动的圆周、圆心的位置及轨道半径不同。
A、B两人的角速度相等,均等于地球的自转角速度。
ωA=ωB== rad/s=7.3×10-5 rad/s
由v=rω得
vA=RAωA=RωA=6.4×106×7.3×10-5m/s=467.2 m/s
vB= RBωB=Rcos 60°ωB=6.4×106×cos 60°×7.3×10-5m/s=233.6 m/s。
答案:ωA=ωB=7.3×10-5rad/s vA=467.2 m/s vB=233.6 m/s
【对点训练】
1.(2021·北京师范大学珠海分校高一月考)观察钟表指针转动情况,回答下列问题
(1)某教室用钟秒针针尖到转轴距离20 cm,求秒针针尖转动的角速度和线速度;
(2)若分针与时针由转轴到针尖的长度之比为2︰1,求分针与时针的角速度之比;
(3)求分针针尖与时针针尖线速度之比。
答案:(1)rad/s, m/s (2)12︰1 (3)24︰1
解析:(1)秒针转动周期为T=60 s,秒针针尖转动的角速度为ω==rad/s,
线速度为v=rω= m/s。
(2)分针转动周期为T1=1 h,时针转动周期为T2=12 h,由ω=可得,角速度与周期成反比,故分针与时针的角速度之比12︰1。
(3)由v=rω可得,分针、时针的线速度之比为=·=×=24。
探究二? 常见的三种传动装置及其特点
【情境导入】
如图为一辆自行车传动装置的结构图,观察自行车是怎样用链条传动来驱动后轮前进的,请思考:
(1)同一齿轮上到转轴距离不同的各点的线速度、角速度是否相同?
(2)两个齿轮相比较,其边缘的线速度大小是否相等?角速度是否相同,转速是否相同?
提示:(1)线速度不同,角速度相同。
(2)线速度大小相等,角速度不同,转速不同。
【要点提炼】
三种传动装置及其特点
同轴传动 皮带传动 齿轮传动
装置 A、B两点在同轴的一个圆盘上 两个轮子用皮带连接,A、B两点分别是两个轮子边缘的点 两个齿轮轮齿啮合,A、B两点s分别是两个齿轮边缘上的点
特点 角速度、周期相同 线速度大小相同 线速度大小相同
转动方向 相同 相同 相反
规律 线速度与半径成正比:= 角速度与半径成反比:=。周期与半径成正比:= 角速度与半径成反比:=。周期与半径成正比:=
特别提醒
在处理传动装置中各物理量间的关系时,关键是确定其相同的量(线速度或角速度),再由描述圆周运动的各物理量间的关系,确定其他各量间的关系。
【典例剖析】
【典题2】 (多选)(2021·四川南充市阆中市川绵外国语学校高一月考)如图所示皮带传送装置,皮带轮O和O′上的三点A、B和C,OA=O′C=r,O′B=2r。则皮带轮转动时A、B、C三点的情况是( AC )
A.vA=vB vB=2vC B.ωA=ωB vB=2vC
C.ωA=2ωB vA=2vC D.ωA=2ωB vA=vC
思路引导:在分析传动装置中各物理量间的关系时,要牢记下面的两个关系:(1)靠皮带、齿轮或摩擦传动的轮子,在不打滑的情况下,轮子边缘上各点的线速度大小相等,角速度则与半径成反比;(2)同一轮子或同轴传动的轮子上各点运动的角速度ω、转速n和周期T均相等,线速度则与半径成正比。
解析:由图可知B点和C点属于同轴传动,所以ωB=ωC,又rB=2rC,根据v=ωr,可知vB=2vC,A、B两点属于皮带传动,所以vA=vB,所以vA=2vC,又rB=2 rA,根据v=ωr,可知ωA=2ωB。故选AC。
【对点训练】
2.(多选)如图所示为一种齿轮传动装置,忽略齿轮啮合部分的厚度,甲、乙两个轮子的半径之比为1︰3,则在传动的过程中( AD )
A.甲、乙两轮的角速度之比为3︰1
B.甲、乙两轮的周期之比为3︰1
C.甲、乙两轮边缘处的线速度之比为3︰1
D.甲、乙两轮边缘上的点相等时间内转过的弧长之比为1︰1
解析:这种齿轮传动,与不打滑的皮带传动规律相同,即两轮边缘的线速度大小相等,故C错误;根据线速度的定义v=可知,弧长Δs=vΔt,故D正确;根据v=ωr可知ω=,又甲、乙两个轮子的半径之比r1︰r2=1︰3,故甲、乙两轮的角速度之比ω1︰ω2=r2︰r1=3︰1,故A正确;周期T=,所以甲、乙两轮的周期之比T1︰T2=ω2︰ω1=1︰3,故B错误。
【易错辨析】
易错点:忽视匀速圆周运动的周期性而致错
【典例】 如图所示,用薄纸做成的圆筒,直径为D,水平放置,绕圆筒轴线OO′以角速度ω0逆时针匀速转动。一玩具手枪发出的子弹,沿水平方向匀速飞来(不计子弹重力影响),沿圆筒的直径方向击穿圆筒后飞出(设薄纸对子弹的运动速度无影响且认为纸筒没有发生形变),结果在圆筒上只留下子弹的一个洞痕,求子弹的速度。
易错分析:认为圆筒只转过π弧度,根据t=,v=得子弹速度v=,这是忽视匀速圆周运动的周期性导致的错误。
正确解答:由于子弹在圆筒上只留下了一个洞痕,考虑匀速圆周运动的周期性,故有π+2nπ=ω0t(n=0,1,2,3,…)
解得t=(n=0,1,2,3,…)
所以v==(n=0,1,2,3,…)。
答案:(n=0,1,2,3,…)
名师点评:子弹穿过圆筒,只留下一个洞痕,圆筒转过的圈数必然为的奇数倍,明确这一点是列出“通式”的关键。本题的解题思路是分别研究两个运动对象,寻找相关量,不要让两个物体的运动互相干扰,导致出现解题失误。
素养警示
解答有关圆周运动的问题时,常出现的错误是没有考虑到圆周运动的周期性而漏解。因此,在解答此类问题时,要特别注意可能会出现的符合题意的多种情况。
【课堂达标检测】
1.(2021·四川南充市阆中市川绵外国语学校高一月考)关于圆周运动,下列说法中正确的是( C )
A.圆周运动可能是匀速运动
B.圆周运动可能是匀变速曲线运动
C.圆周运动一定是非匀变速运动
D.圆周运动加速度可能不变
解析:圆周运动是曲线运动,因此合外力不等于零。圆周运动的加速度方向是在变化的,所以圆周运动一定是非匀变速运动。故选C。
2.(2021·天津市第八中学高一月考)一户外健身器材如图所示,当器材上轮子转动时,轮子上A、B两点的( C )
A.转速nB>nA B.周期TB>TA
C.线速度vB>vA D.角速度ωB>ωA
解析:由于同轴转动,轮上各个点的角速度相同(圆心除外),所以A、B两点的角速度相同,转速相同,周期相同,ABD错误;由v=ωr,线速度vB>vA,C正确。
3.(2021·浙江高一月考)走时准确的时钟,时针和分针的角速度之比( A )
A.1︰12 B.12︰1
C.1︰60 D.60︰1
解析:时针转一圈需要12个小时,分针转一圈需要1小时,故其角速度之比为ω时:ω分=︰=1︰12,故选A。
4.(多选)(2021·江苏扬州市扬州中学高一月考)如图所示为某一皮带传动装置,主动轮的半径为r1,从动轮的半径为r2,已知主动轮做顺时针转动,转速为n,转动过程中皮带不打滑。下列说法正确的是( BC )
A.从动轮做顺时针转动
B.从动轮做逆时针转动
C.从动轮的转速为n
D.从动轮的转速为n
解析:主动轮做顺时针转动,由皮带缠绕的方式知从动轮做逆时针转动,B正确,A错误;两轮边缘的线速度大小相等,由v=rω,ω=2πn可知,2πn·r1=2πn′·r2,解得从动轮的转速n′=n,C正确,D错误。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
