18.2.2菱形的性质 课件(共20张PPT)人教版数学八年级下册
文档属性
| 名称 | 18.2.2菱形的性质 课件(共20张PPT)人教版数学八年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
18.2.2 菱 形
第1课时 菱形的性质
第十八章 平行四边形
学习目标
1.了解菱形的概念及其与平行四边形的关系.
2.探索并证明菱形的性质定理.(重点)
3.应用菱形的性质定理解决计算或证明问题.(难点)
下面的图形中有你熟悉的吗?
导入新知
平行
四边形
矩形
前面我们学行四边形和矩形,知道了矩形是由平行四边形角的变化得到,如果平行四边形有一个角是直角时,就成为了矩形.
有一个角是直角
探究新知
知识点 1
菱形的定义
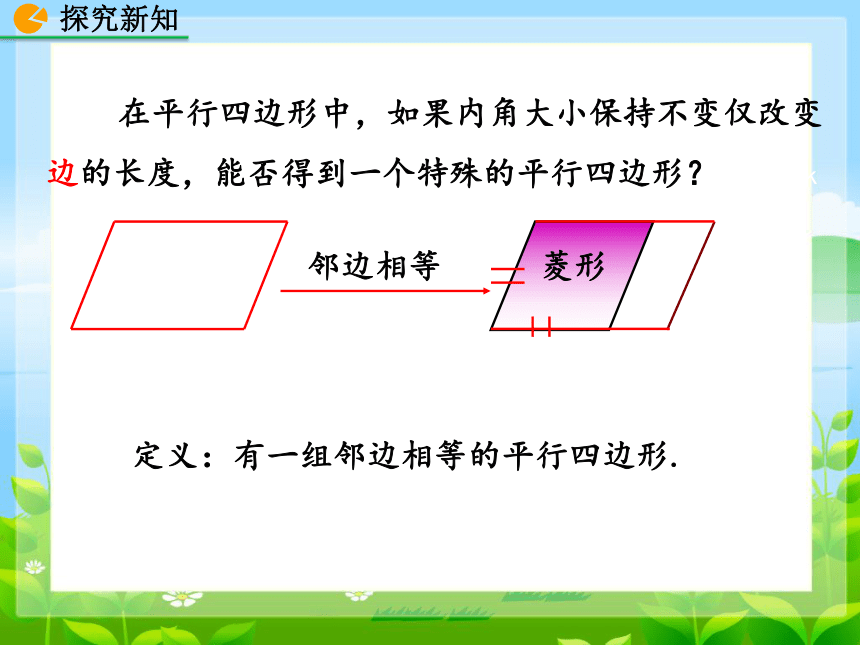
在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?``x``xk
探究新知
菱形
邻边相等
定义:有一组邻边相等的平行四边形.
有一组 的
邻边相等
平行四边形叫做
A
D
C
B
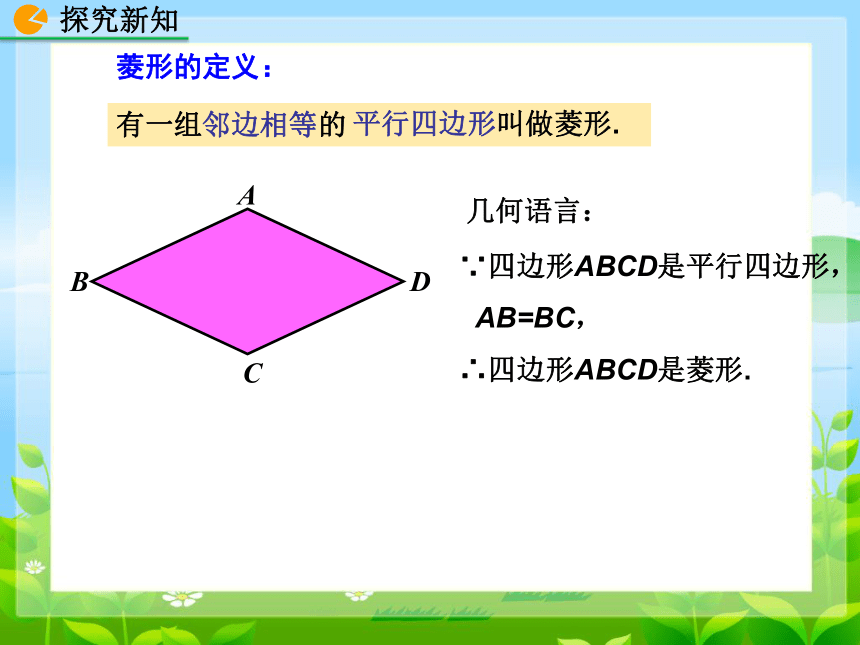
∵四边形ABCD是平行四边形,
AB=BC,
∴四边形ABCD是菱形.
菱形.
探究新知
菱形的定义:
几何语言:
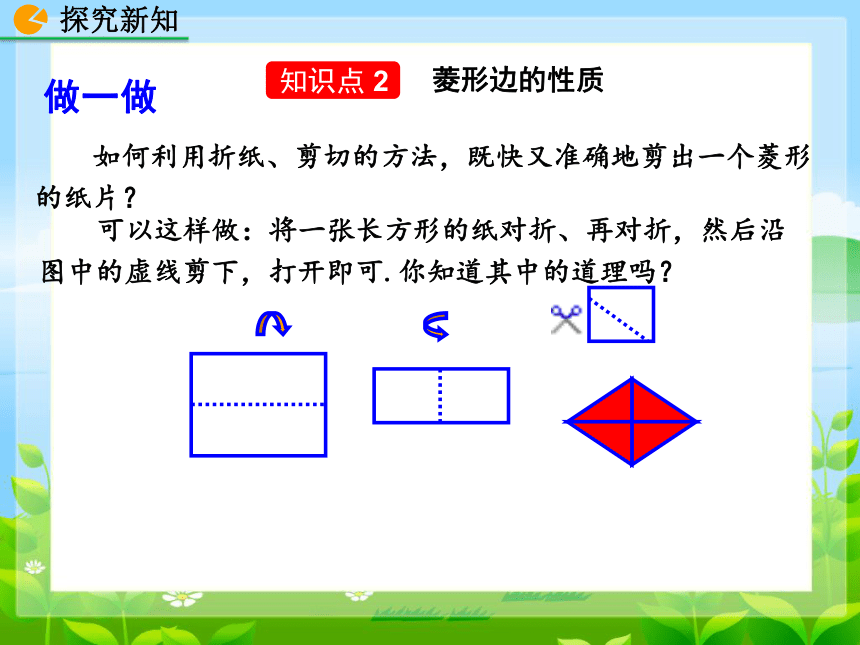
可以这样做:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
做一做
探究新知
知识点 2
菱形边的性质
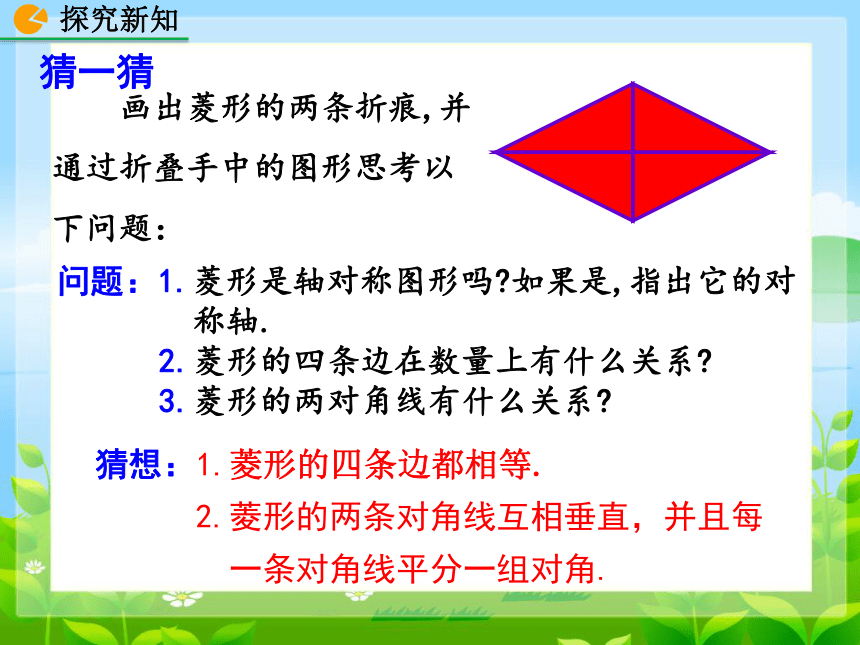
画出菱形的两条折痕,并通过折叠手中的图形思考以下问题:
探究新知
问题:1.菱形是轴对称图形吗 如果是,指出它的对
称轴.
2.菱形的四条边在数量上有什么关系
3.菱形的两对角线有什么关系
猜想:1.菱形的四条边都相等.
2.菱形的两条对角线互相垂直,并且每
一条对角线平分一组对角.
猜一猜
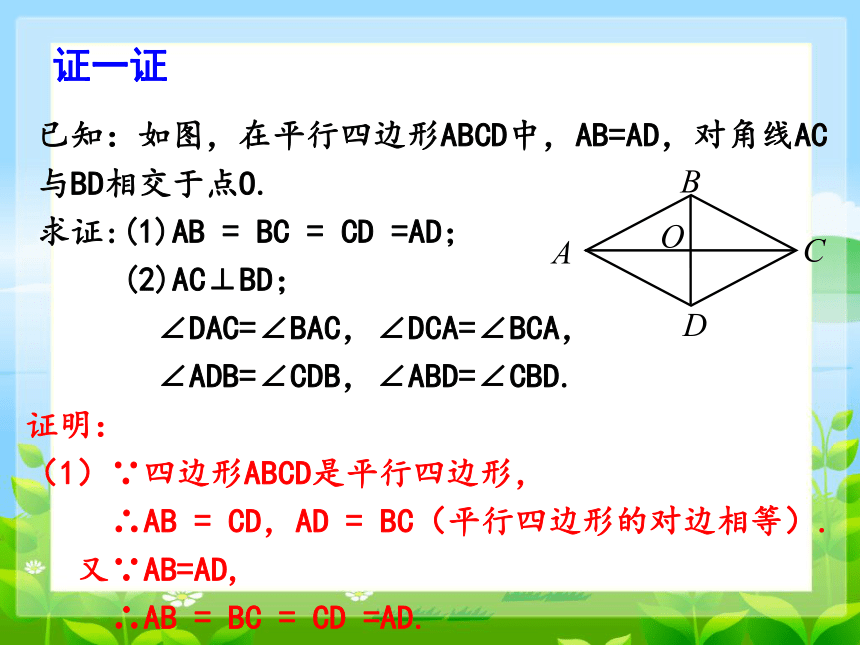
已知:如图,在平行四边形ABCD中,AB=AD,对角线AC与BD相交于点O.
求证:(1)AB = BC = CD =AD;
(2)AC⊥BD;
∠DAC=∠BAC,∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.
证明:
(1)∵四边形ABCD是平行四边形,
∴AB = CD,AD = BC(平行四边形的对边相等).
又∵AB=AD,
∴AB = BC = CD =AD.
A
B
C
O
D
证一证
(2)∵AB = AD,
∴△ABD是等腰三角形.
又∵四边形ABCD是平行四边形,
∴OB = OD (平行四边形的对角线互相平分).
在等腰三角形ABD中,
∵OB = OD,
∴AO⊥BD,AO平分∠BAD,
即AC⊥BD,∠DAC=∠BAC.
同理可证∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.
A
B
C
O
D
探究新知
菱形的性质:
1.菱形的四条边都相等.
2.菱形的两条对角线互相垂直,并且每一条对
角线平分一组对角.
符号语言:
∵四边形ABCD是菱形,
∴AB=BC=CD=AD;
A
B
C
O
D
AC平分∠BAD和∠BCD ;
BD平分∠ABC和∠ADC.
AC⊥BD ;
猜想证明 形成性质
我们得到了菱形的性质.如果把矩形和菱形的性质进行比较,发现它们很相似.你能写出矩形、菱形的定义及它们的特殊性质并进行比较吗?
矩形和菱形特殊性质比较
平行四边形
矩形
菱形
一个角是直角
一组邻角相等
一组邻边相等
四个角是直
角(相等)
对角线
相等
四条边
相等
对角线互
相垂直
轴对称性
对边相等
四个角都是直角
对角线互相平分且相等
四边相等
对角相等
两条对角线互相垂直平分,并且每一条对角线平分一组对角
平行四边形的性质
矩形的性质
菱形的性质
对边相等
对角相等
对角线互相平分
比一比,猜一猜,填写下表:
探究新知
菱形是特殊的平行四边形,
那么能否利用平行四边形面积公式计算菱形的面积呢
菱形
A
B
C
D
O
E
【思考】计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积吗
探究新知
知识点 3
菱形的面积
S菱形=BC× AE.
如图,四边形ABCD是菱形,对角线AC,BD交于点O,试用对角线表示出菱形ABCD的面积.
A
B
C
D
O
解:∵四边形ABCD是菱形,
∴AC⊥BD.
∴S菱形ABCD = S△ABC + S△ADC
= AC·BO+ AC·DO
= AC(BO+DO)
= AC·BD.
菱形的面积 = 底×高 = 对角线乘积的一半
探究新知
例 如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(结果分别精确到0.01m和0.1m2).
A
B
C
D
O
解:∵花坛ABCD是菱形,
应用新知
例 1
利用菱形的面积公式解答问题
在Rt△OAB中,
∴ .
∴ .
1.已知菱形的周长是36cm,那么它的边长是______.
巩固练习
9cm
2.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC , BD的长.
O
C
B
D
A
5
4
3
3.菱形ABCD的两条对角线BD,AC长分别是6cm和8cm,求菱形周长和面积.
菱形的性质及有关计算
菱形的性质
有关计算
边
1.周长=边长的四倍;
2.面积=底×高=两条对角线乘积的一半
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
课堂小结
1.如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
A.2.4cm B.4.8cm C.5cm D.9.6cm
B
课堂检测
基础巩固题
2.如图,在菱形ABCD中,已知∠A=60°,AB=5,则△ABD的周长是 ( )
A.10 B.12 C.15 D.20
A
B
C
D
3.如图,菱形ABCD的周长为48cm,对角线AC , BD相交于O点,E是AD的中点,连接OE,则线段OE的长为_______.
O
A
B
C
D
E
4.如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是8cm.求:(1)两条对角线的长度;(2)菱形的面积.
O
A
B
C
D
18.2.2 菱 形
第1课时 菱形的性质
第十八章 平行四边形
学习目标
1.了解菱形的概念及其与平行四边形的关系.
2.探索并证明菱形的性质定理.(重点)
3.应用菱形的性质定理解决计算或证明问题.(难点)
下面的图形中有你熟悉的吗?
导入新知
平行
四边形
矩形
前面我们学行四边形和矩形,知道了矩形是由平行四边形角的变化得到,如果平行四边形有一个角是直角时,就成为了矩形.
有一个角是直角
探究新知
知识点 1
菱形的定义
在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?``x``xk
探究新知
菱形
邻边相等
定义:有一组邻边相等的平行四边形.
有一组 的
邻边相等
平行四边形叫做
A
D
C
B
∵四边形ABCD是平行四边形,
AB=BC,
∴四边形ABCD是菱形.
菱形.
探究新知
菱形的定义:
几何语言:
可以这样做:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
做一做
探究新知
知识点 2
菱形边的性质
画出菱形的两条折痕,并通过折叠手中的图形思考以下问题:
探究新知
问题:1.菱形是轴对称图形吗 如果是,指出它的对
称轴.
2.菱形的四条边在数量上有什么关系
3.菱形的两对角线有什么关系
猜想:1.菱形的四条边都相等.
2.菱形的两条对角线互相垂直,并且每
一条对角线平分一组对角.
猜一猜
已知:如图,在平行四边形ABCD中,AB=AD,对角线AC与BD相交于点O.
求证:(1)AB = BC = CD =AD;
(2)AC⊥BD;
∠DAC=∠BAC,∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.
证明:
(1)∵四边形ABCD是平行四边形,
∴AB = CD,AD = BC(平行四边形的对边相等).
又∵AB=AD,
∴AB = BC = CD =AD.
A
B
C
O
D
证一证
(2)∵AB = AD,
∴△ABD是等腰三角形.
又∵四边形ABCD是平行四边形,
∴OB = OD (平行四边形的对角线互相平分).
在等腰三角形ABD中,
∵OB = OD,
∴AO⊥BD,AO平分∠BAD,
即AC⊥BD,∠DAC=∠BAC.
同理可证∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.
A
B
C
O
D
探究新知
菱形的性质:
1.菱形的四条边都相等.
2.菱形的两条对角线互相垂直,并且每一条对
角线平分一组对角.
符号语言:
∵四边形ABCD是菱形,
∴AB=BC=CD=AD;
A
B
C
O
D
AC平分∠BAD和∠BCD ;
BD平分∠ABC和∠ADC.
AC⊥BD ;
猜想证明 形成性质
我们得到了菱形的性质.如果把矩形和菱形的性质进行比较,发现它们很相似.你能写出矩形、菱形的定义及它们的特殊性质并进行比较吗?
矩形和菱形特殊性质比较
平行四边形
矩形
菱形
一个角是直角
一组邻角相等
一组邻边相等
四个角是直
角(相等)
对角线
相等
四条边
相等
对角线互
相垂直
轴对称性
对边相等
四个角都是直角
对角线互相平分且相等
四边相等
对角相等
两条对角线互相垂直平分,并且每一条对角线平分一组对角
平行四边形的性质
矩形的性质
菱形的性质
对边相等
对角相等
对角线互相平分
比一比,猜一猜,填写下表:
探究新知
菱形是特殊的平行四边形,
那么能否利用平行四边形面积公式计算菱形的面积呢
菱形
A
B
C
D
O
E
【思考】计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积吗
探究新知
知识点 3
菱形的面积
S菱形=BC× AE.
如图,四边形ABCD是菱形,对角线AC,BD交于点O,试用对角线表示出菱形ABCD的面积.
A
B
C
D
O
解:∵四边形ABCD是菱形,
∴AC⊥BD.
∴S菱形ABCD = S△ABC + S△ADC
= AC·BO+ AC·DO
= AC(BO+DO)
= AC·BD.
菱形的面积 = 底×高 = 对角线乘积的一半
探究新知
例 如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(结果分别精确到0.01m和0.1m2).
A
B
C
D
O
解:∵花坛ABCD是菱形,
应用新知
例 1
利用菱形的面积公式解答问题
在Rt△OAB中,
∴ .
∴ .
1.已知菱形的周长是36cm,那么它的边长是______.
巩固练习
9cm
2.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC , BD的长.
O
C
B
D
A
5
4
3
3.菱形ABCD的两条对角线BD,AC长分别是6cm和8cm,求菱形周长和面积.
菱形的性质及有关计算
菱形的性质
有关计算
边
1.周长=边长的四倍;
2.面积=底×高=两条对角线乘积的一半
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
课堂小结
1.如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
A.2.4cm B.4.8cm C.5cm D.9.6cm
B
课堂检测
基础巩固题
2.如图,在菱形ABCD中,已知∠A=60°,AB=5,则△ABD的周长是 ( )
A.10 B.12 C.15 D.20
A
B
C
D
3.如图,菱形ABCD的周长为48cm,对角线AC , BD相交于O点,E是AD的中点,连接OE,则线段OE的长为_______.
O
A
B
C
D
E
4.如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是8cm.求:(1)两条对角线的长度;(2)菱形的面积.
O
A
B
C
D
