人教版七年级下册数学课时训练(含解析)第五章第三节平行线的性质——第一课时平行线的性质
文档属性
| 名称 | 人教版七年级下册数学课时训练(含解析)第五章第三节平行线的性质——第一课时平行线的性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 200.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-31 08:27:13 | ||
图片预览

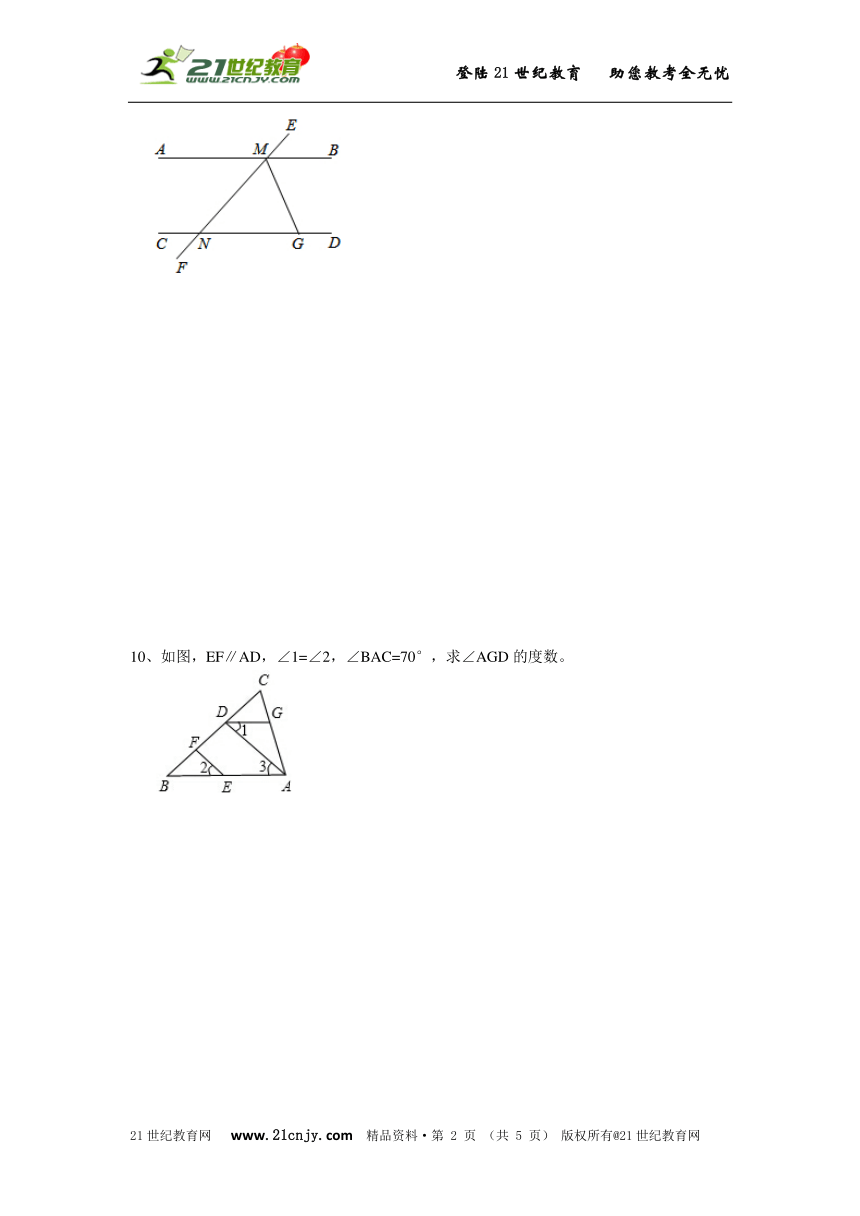
文档简介
平行线的性质第一课时——平行线的性质
一、选择题。
1、如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
A.132° B.134° C.136° D.138°
第1题图 第2题图 第3题图 第4题图
2、如图,直线a∥b,直角三角形ABC的顶点B在直线a上,点C=90°,∠β=55°,则
∠α的度数为( )
A.15° B.25° C.35° D.55°
3、如图,在五边形ABCDE中,∠CDE=80°,为了保证AE∥BC,则∠BCD+∠AED应等于( )21世纪教育网版权所有
A.100° B.260° C.280° D.275°
4、如图,能使AB∥CD的条件是( )
A.∠B=∠D B. ∠D+∠B=90° C. ∠B+∠D+∠E=180° D. ∠B+∠D=∠E
二、填空题。
5、如图,AB∥CD,AD=CD,∠1=70°,则∠2的度数是___________。
6、如图,直线m∥n,△ABC为等腰三角形,∠BAC=90°,则∠1=_______度。
第5题图 第6题图 第7题图 第8题图
7、如图,直线a∥b,三角板的直角顶点A落在直线a上,两条直线分别交直线b于B、C两点。若∠1=42°,则∠2的度数是_________。21教育网
8、如图,∥,∠α=∠β,∠1=40°,则∠2=______°
三、解答题。
9、如图,AB∥CD,EF分别交AB、CD于M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠MGC的度数。21cnjy.com
10、如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数。
参考答案及解析
1、答案:B。
解析:【解答】
如图:
过点E作EF∥AB。
∵AB∥CD,∴AB∥CD∥AB
∴∠C=∠FEC,∠BAE=∠FEA
∵∠C=44°,∠AEC为直角
∴∠FEC=44°,∠BAE=∠FEA=90°-44°=46°
∴∠1=180°-∠BAE=180°-46°=134°
故选B。
3、答案:C
解析:【解答】
过点D作DF∥AE,如图:
∵DF∥AE,∴∠AED+∠EDF=180°
为了使AE∥BC,只需要DF∥BC即可。
∴只要∠FDC+∠BCD=180°,则DF∥BC
∴(∠AED+∠EDF)+(∠FDC+∠BCD)=360°
又∠CDE=80°,∠CDE=∠EDF+∠FDC
∴∠AED+∠BCD=360°-80°=280°
故选C。
5、答案:40°
解析:【解答】∵AB∥CD,∠1=70°,
∴∠ACD=∠1=70°
∵AD=CD
∴∠CAD=∠ACD=70°
∴∠2=180°-∠ACD-∠CAD=180°-70°-70°=40°
故答案为40°。
【分析】本题考查了平行线的性质,三角形内角和。
6、答案:45
解析:【解答】∵△ABC是等腰三角形,∠BAC=90°
∴∠ABC=∠ACB=45°
∵m∥n
∴∠1=∠ABC=45°
故答案为45。
【分析】本题考查了等腰三角形的性质、三角形内角和、平行线的性质的应用。
7、答案:48°
解析:【解答】
∵∠BAC=90°,∠1=42°
∴∠3=90°-∠1=90°-42°=48°
∵直线a∥b,
∴∠2=∠3=48°
故答案是48°。
【分析】本题考查平行线的性质、互余的角。
8、答案:140°
解析:【解答】如图
∵∥,∴∠3=∠1=40°
∵∠α=∠β,∴AB∥CD ∴∠2+∠3=180°
解:∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等)
∵∠1=∠2(已知)
∴∠1=∠3(等量代换)
∴DG∥AB(内错角相等,两直线平行)
∴∠AGD+∠BAC=180°(两直线平行,同旁内角互补)
∵∠BAC=70°
∴∠AGD=180°-∠BAC=180°-70°=110°。
【分析】本题考查了平行线的性质与判定。
一、选择题。
1、如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
A.132° B.134° C.136° D.138°
第1题图 第2题图 第3题图 第4题图
2、如图,直线a∥b,直角三角形ABC的顶点B在直线a上,点C=90°,∠β=55°,则
∠α的度数为( )
A.15° B.25° C.35° D.55°
3、如图,在五边形ABCDE中,∠CDE=80°,为了保证AE∥BC,则∠BCD+∠AED应等于( )21世纪教育网版权所有
A.100° B.260° C.280° D.275°
4、如图,能使AB∥CD的条件是( )
A.∠B=∠D B. ∠D+∠B=90° C. ∠B+∠D+∠E=180° D. ∠B+∠D=∠E
二、填空题。
5、如图,AB∥CD,AD=CD,∠1=70°,则∠2的度数是___________。
6、如图,直线m∥n,△ABC为等腰三角形,∠BAC=90°,则∠1=_______度。
第5题图 第6题图 第7题图 第8题图
7、如图,直线a∥b,三角板的直角顶点A落在直线a上,两条直线分别交直线b于B、C两点。若∠1=42°,则∠2的度数是_________。21教育网
8、如图,∥,∠α=∠β,∠1=40°,则∠2=______°
三、解答题。
9、如图,AB∥CD,EF分别交AB、CD于M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠MGC的度数。21cnjy.com
10、如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数。
参考答案及解析
1、答案:B。
解析:【解答】
如图:
过点E作EF∥AB。
∵AB∥CD,∴AB∥CD∥AB
∴∠C=∠FEC,∠BAE=∠FEA
∵∠C=44°,∠AEC为直角
∴∠FEC=44°,∠BAE=∠FEA=90°-44°=46°
∴∠1=180°-∠BAE=180°-46°=134°
故选B。
3、答案:C
解析:【解答】
过点D作DF∥AE,如图:
∵DF∥AE,∴∠AED+∠EDF=180°
为了使AE∥BC,只需要DF∥BC即可。
∴只要∠FDC+∠BCD=180°,则DF∥BC
∴(∠AED+∠EDF)+(∠FDC+∠BCD)=360°
又∠CDE=80°,∠CDE=∠EDF+∠FDC
∴∠AED+∠BCD=360°-80°=280°
故选C。
5、答案:40°
解析:【解答】∵AB∥CD,∠1=70°,
∴∠ACD=∠1=70°
∵AD=CD
∴∠CAD=∠ACD=70°
∴∠2=180°-∠ACD-∠CAD=180°-70°-70°=40°
故答案为40°。
【分析】本题考查了平行线的性质,三角形内角和。
6、答案:45
解析:【解答】∵△ABC是等腰三角形,∠BAC=90°
∴∠ABC=∠ACB=45°
∵m∥n
∴∠1=∠ABC=45°
故答案为45。
【分析】本题考查了等腰三角形的性质、三角形内角和、平行线的性质的应用。
7、答案:48°
解析:【解答】
∵∠BAC=90°,∠1=42°
∴∠3=90°-∠1=90°-42°=48°
∵直线a∥b,
∴∠2=∠3=48°
故答案是48°。
【分析】本题考查平行线的性质、互余的角。
8、答案:140°
解析:【解答】如图
∵∥,∴∠3=∠1=40°
∵∠α=∠β,∴AB∥CD ∴∠2+∠3=180°
解:∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等)
∵∠1=∠2(已知)
∴∠1=∠3(等量代换)
∴DG∥AB(内错角相等,两直线平行)
∴∠AGD+∠BAC=180°(两直线平行,同旁内角互补)
∵∠BAC=70°
∴∠AGD=180°-∠BAC=180°-70°=110°。
【分析】本题考查了平行线的性质与判定。
