2024-2025年人教版九年级上册数学期末专题提升训练05:一元二次方程的应用(与图形相关的问题)(含解析)
文档属性
| 名称 | 2024-2025年人教版九年级上册数学期末专题提升训练05:一元二次方程的应用(与图形相关的问题)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-07 14:51:34 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
专题 05:一元二次方程的应用(与图形相关的问题)--2024-2025年人教版九年级上册数学期末专题提升训练
1.如图,老李想用长为的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈,并在边上留一个宽的门(建在处,另用其他材料).设的长是.
AI
(1)填空:______;
(2)若羊圈的面积是,求的值.
2.某社区为了解决停车难的问题,利用一块矩形空地建了一个小型停车场,其布局如图所示.已知,,阴影部分设计为停车位,其余部分均为宽度为米的道路.已知停车位的面积(即阴影面积)为.
(1)求道路的宽是多少米?
(2)该停车场共有车位70个,据调查分析,当每个车位的月租金为300元时,可全部租出;若每个车位的月租金每上涨5元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为21120元,同时尽可能让利于居民?
3.月日中华人民共和国国家勋章和国家荣誉称号颁授仪式在人民大会堂隆重举行,我国小麦远缘杂交育种奠基人和农业发展战略专家李振声,在祖国西北耕耘载,培育推广抗病、高产的远缘杂交小麦,被授予“共和国勋章”.某校八年级学生利用课余时间进行劳动实践,准备种植远缘杂交小麦,试验田一边靠学校的墙(墙的最大可用长度为),其他边用长为的篱笆(篱笆正好全部用完,且不考虑接头的部分)围成中间隔有一道篱笆的长方形,在试验田的前端设计了两个宽的小门,供同学们进出.设试验田的一边的长为.
(1)求当为何值时,围成的试验田面积为;
(2)能围成面积为的试验田吗?请通过计算说明理由.
4.素材1:图是拟建中的一个温室平面设计图纸,图纸上1个单位长度代表实际距离1米,温室是一个矩形,其周长为120,准备在它的四周铺设道路,左右两条纵向道路的宽度都为1,上边横向道路的宽度为1,下边横向道路的宽度为3,中间部分(阴影部分)种植草莓,种植面积为720.
素材2:道路的路面造价是70元平方米;经市场调查,草莓培育一年可产果,已知每平方米的草莓销售平均利润为100元;其余费用为3万元.
任务1:(1)实际中温室的长不能大于35米,通过计算说明拟建的温室是否达标;
任务2:(2)求经过1年后,温室年净利润为多少?(净利润=草莓销售的总利润-路面造价费用-其余费用)
5.某扶贫单位为了提高贫困户的经济收入,购买了的铁栅栏,准备用这些铁栅栏为贫困户靠墙(墙长)围建一个中间带有铁栅栏的矩形养鸡场(如图所示).
(1)若要建的矩形养鸡场面积为,求鸡场的长和宽;
(2)该扶贫单位想要建一个的矩形养鸡场,这一想法能实现吗?请说明理由.
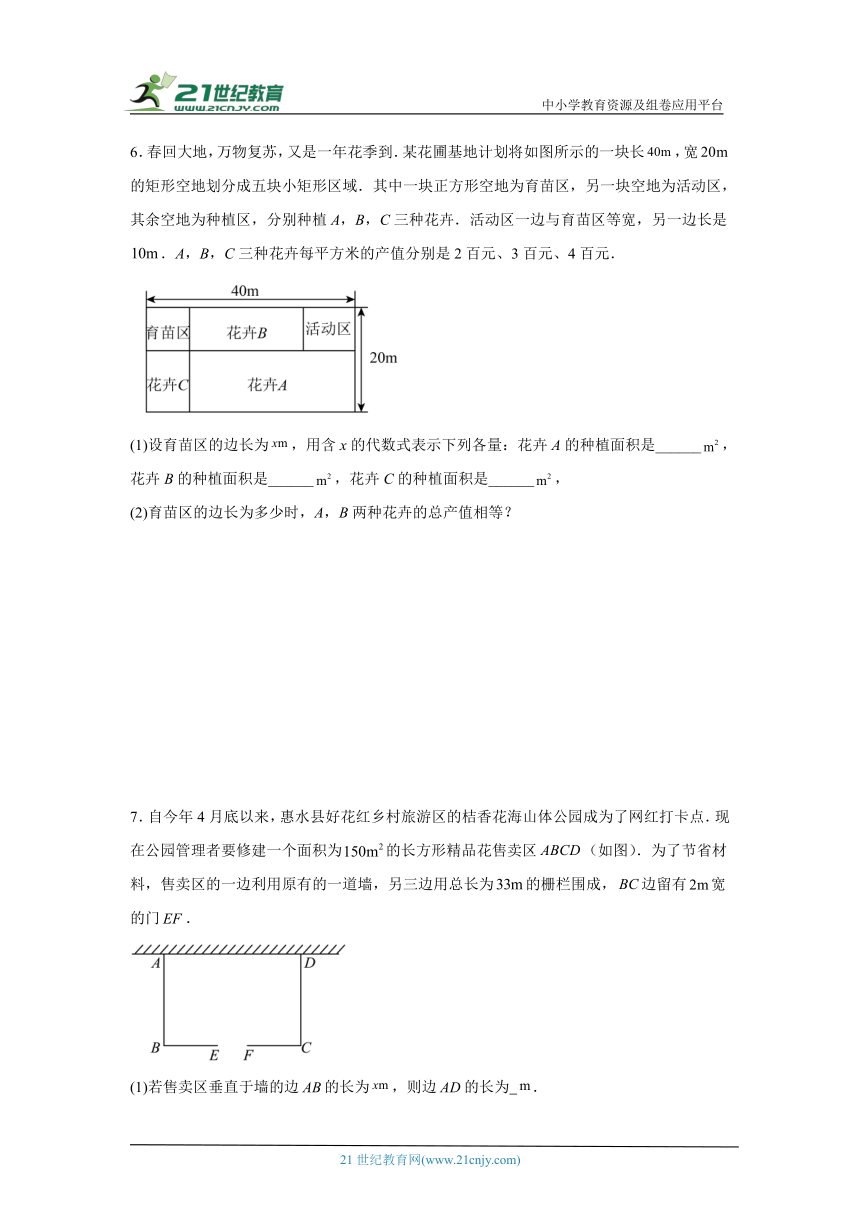
6.春回大地,万物复苏,又是一年花季到.某花圃基地计划将如图所示的一块长,宽的矩形空地划分成五块小矩形区域.其中一块正方形空地为育苗区,另一块空地为活动区,其余空地为种植区,分别种植A,B,C三种花卉.活动区一边与育苗区等宽,另一边长是.A,B,C三种花卉每平方米的产值分别是2百元、3百元、4百元.
(1)设育苗区的边长为,用含x的代数式表示下列各量:花卉A的种植面积是______,花卉B的种植面积是______,花卉C的种植面积是______,
(2)育苗区的边长为多少时,A,B两种花卉的总产值相等?
7.自今年4月底以来,惠水县好花红乡村旅游区的桔香花海山体公园成为了网红打卡点.现在公园管理者要修建一个面积为的长方形精品花售卖区(如图).为了节省材料,售卖区的一边利用原有的一道墙,另三边用总长为的栅栏围成,边留有宽的门.
(1)若售卖区垂直于墙的边的长为,则边的长为 .
(2)若墙足够长,则售卖区的长和宽各为多少米?
(3)当围成的售卖区只有一种围法时,求墙长a的取值范围.
8.如图,有一块长为,宽为的矩形耕地,为方便灌溉,现需在耕地上挖两条宽度相等的水渠,水渠把耕地分成面积均为的个矩形小块,求水渠的宽度.
9.同学们开展的综合实践活动中取得了系列丰硕的成果,需要推广宣传.原计划使用一块正方形场地布展,后经过研究,发现长与宽之比为的长方形场地展览效果更好,因此需要把长增加6米,宽增加2米(如图1).
(1)直接写出长方形区域的宽是_______m,长是_______m.
(2)现计划将长方形区域按图2的方式进行划分,展示四各小组的项目成果,在各展区之间留宽度相等的过道.如果各展区的总面积为,求过道的宽度.
10.某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙的长度不限),另外三边用木栏围成,木栏长.
(1)怎样围成一个面积为的矩形场地?
(2)能围成面积能为的矩形场地吗?若不能,说明理由?
11.宫格画(图1)因其独特的艺术性近年来受到年轻人的追捧.如图2,小欣利用宽度相等的纸卡(灰色阴影部分)制作了一个长为,宽为的宫格画画框,空白处的宽度相同,设纸卡的宽为.
(1)图2中空白处的宽度_________.(用含x的式子表示)
(2)若图2中空白处的面积为,求x的值.
12.某公司展销如图所示的长方形工艺品,该工艺品长,宽,中间镶有宽度相同的三条彩色图案.
(1)若除去彩色图案后剩余的面积为,设彩色图案的宽度为,则可列方程为______;(要求用原数列方程,不要求化简)
(2)已知该工艺品的成本是元/件,物价局规定销售单价在元至元的范围内,如果以单价元/件销售,那么每天可售出件,另外每天除工艺品的成本外所需支付的各种费用是元,根据销售经验,如果将销售单价每上涨元,每天就少售出件.请问该公司每天把销售单价定为多少元时所获利润为元?
13.综合与实践
如图1,有一张长,宽的长方形硬纸片,截去四个大小相同小正方形之后,折成如图2所示的长方体形的无盖纸盒,设截取的小正方形边长为.
(1)用含有x的代数式分别表示无盖纸盒底面的长(________),宽(________);
(2)若纸盒的底面积为,求小正方形边长为x的值;
(3)求出(2)中长方体纸盒的容积.
14.如图,有长为的篱笆,一面利用墙(墙长为),围成如图所示的矩形花圃.
(1)如果要围成面积为的花圃,那么的长为多少米?
(2)能否围成面积为的花圃?若能,求出的长;若不能,请说明理由.
15.如图,某儿童乐园的场地是长宽分别为,的矩形.儿童乐园进行改造升级,场地也进行扩充,将场地的长、宽增加相同的长度后,新场地仍是一个矩形.
(1)若扩充后的矩形场地面积为,求新的矩形场地的长与宽;
(2)儿童乐园改造升级后,经过调查发现,票价30元/人时游客数为每天500人,票价每提高1元,则游客减少10人,要使得儿童乐园日营业额达到1.6万元,票价应定为多少元?
16.如图,某农场有两堵互相垂直的墙,长度分别为27米和15米,该农场打算借这两堵墙建一个长方形饲养场,其中和两边借助墙体且不超出墙体,其余部分用总长45米的木栏围成,中间预留1米宽的通道,在和边上各留1米宽的门、设长x米,
(1)求的长度(用含x的代数式表示).
(2)若饲养场的面积为180平方米,求x的值.
17.如图,现准备用32米长的木板建有关面积为130平方米的长方形仓库,仓库的一边靠墙,并在与墙垂直的一边开一道1米宽的小门.
(1)如果墙长15米,求仓库的长和宽;
(2)如果墙长a米,在离开墙9米开外仓库一侧修条小路,那么墙长至少要多少米?
18.学校计划利用一片空地建一个长方形自行车车棚,其中一面靠墙,墙的长度为8米.在与墙平行的一面开一个2米宽的门,已知现有的木板材料可修建的总长为26米,且全部用于除墙外其余三面外墙的修建.
(1)长方形车棚与墙垂直的一面至少为__________米;
(2)如图,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路(如图中阴影),若车棚与墙垂直的一面长按(1)中的最小长度,则停放电动车的区域面积能否达到54平方米,若能,此时小路的宽度是多少米?若不能,请说明理由.
19.如图,用一条长的绳子围成矩形,设边的长为.
(1)边的长为______,矩形的面积为______(均用含的代数式表示);
(2)矩形的面积是否可以是?请给出你的结论,并用所学的方程或者函数知识说明理由.
20.山西槐米茶,口感清香,冲泡汤色亮黄,味道醇厚,具有清血凉血,抗菌消炎等功效.
(1)如图1,太原市某茶庄种植槐米茶,由于规模不断扩大,现计划开阔一块面积为600平方米的长方形采茶基地,已知该采茶基地的长比宽多10米.
①分别求该采茶基地的长和宽;
②若要在采茶基地的四周围上篱笆,问需要多长的篱笆?
(2)如图2,该茶庄开设了一片观光园区,园区内原有一块长方形空地,该空地与(1)中的采茶基地大小、形状相同,后计划在此区域栽种鲜花(阴影部分)并铺设如图所示的宽度相同的小路(空白部分)供游客观光,若鲜花的种植面积为486平方米,求小路的宽度.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1);
(2)或.
【分析】本题考查了一元二次方程的应用及列代数式,解题的关键是要理解题意,能正确列出方程.
(1)根据栅栏总长列式即可;
(2)利用矩形面积公式即可求解.
【详解】(1)解:设的长是,则
,
故答案为:;
(2)解:根据题意:,
整理得:,
解得:,,
∴的值为或.
2.(1)道路的宽是4米
(2)每个车位的月租金上涨20元时,停车场的月租金收入为21120元
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)道路的宽为米,根据铺花砖的面积(即阴影面积)为,结合其布局图,列出一元二次方程,解方程取符合题意的值即可;
(2)设每个车位的月租金上涨元时,停车场的月租金收入为21120元,根据“该停车场共有车位70个,据调查分析,当每个车位的月租金为300元时,可全部租出;若每个车位的月租金每上涨5元,就会少租出1个车位”,列出一元二次方程,解方程取尽可能让利于居民的值即可.
【详解】(1)解:道路的宽为米,
由题意得:,
整理得:,
解得:(不合题意,舍去),,
答:道路的宽是4米;
(2)解:设每个车位的月租金上涨元时,停车场的月租金收入为21120元,
由题意得:,
整理得:,
解得:,
∵尽可能让利于居民,
,
答:每个车位的月租金上涨20元时,停车场的月租金收入为21120元.
3.(1)当为时,围成的试验田面积为
(2)不能围成面积为的试验田,理由见解析
【分析】本题考查了一元二次方程的应用,解题的关键是理解题意,正确找出等量关系.
(1)设试验田的一边的长为,则,根据长方形的面积列方程即可求解;
(2)根据题意列出方程,再利用一元二次方程根的判别式即可判断.
【详解】(1)解:设试验田的一边的长为,则,
根据题意可得:,
解得:或,
当时,,不合题意,舍去,
当为时,围成的试验田面积为;
(2)不能围成面积为的试验田,理由如下:
根据题意可得:,
整理得:,
,
该方程无实数根,
即不能围成面积为的试验田.
4.任务:(1)温室达标,详见解析;
任务:(2)元
【分析】本题考查了一元二次方程的应用,根据题意正确列出一元二次方程是解题的关键.
(1)设,则,,,由题意得,,解方程即可得到答案;
(2)根据题意正确列算式,求解即可.
【详解】解:任务:(1)设,
则,,,
根据题意得,,即,
解得,
∵,
∴,
∴,
∵,
∴温室达标;
任务:(2)由(1)知,,
∴温室的面积为,
∴道路面积为,
∴道路总造价为,
∴草莓的总利润为,
∴净利润为
答:温室年净利润为元 .
5.(1)长和宽分别为与
(2)不能,理由见解析
【分析】本题考查一元二次方程的实际应用,能根据几何图形正确列出方程是解题的关键.
(1)设,则,根据面积列出方程,求解验根即可;
(2)设,则,根据面积列出方程,利用根的判别式判断方程是否有解,并是否符合题意,即可解决.
【详解】(1)解:设,
∵铁栅栏总长为,
∴,
由题意得:,
整理得:,
解得:,,
当时,,不符合题意;
当时,,符合题意;
答:鸡场的长和宽分别为与;
(2)解:设,则,
由题意得:,
整理得:,
∵,
∴方程无解,
故这一想法不能实现.
6.(1);;
(2)
【分析】本题考查的是列代数式,整式乘法的应用,一元二次方程的应用,根据题意正确列出代数式是解题的关键.
(1)根据题意可知:花卉A的种植面积是:;花卉B的种植面积是:;花卉C的种植面积是:;
(2)先计算出A,B两种种花卉的总产值分别是百元、百元,根据A,B两种花卉的总产值相等,可得,求解即可.
【详解】(1)解:根据题意可知:
花卉A的种植面积是:;
花卉B的种植面积是;
花卉C的种植面积是:;
故答案为:;;.
(2)解:两种花卉每平方米的产值分别是2百元、3百元,
,B两种花卉的总产值分别百元、百元,
,B两种花卉的总产值相等,
,
解得:(舍去)或,
∴育苗区的边长为时,A,B两种花卉的总产值相等.
7.(1)
(2)售卖区的长为,宽为或长为,宽为.
(3).
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)设垂直于墙的边长为,可得平行于墙的边长为,整理即可;
(2)根据矩形的面积公式结合养鸡场的面积为,列出一元二次方程,解之即可得出结论;
(3)根据(1)的结论可分、及三种情况,找出题目解的个数,即可得出结论.
【详解】(1)解:∵售卖区垂直于墙的边的长为,
∴边的长为.
(2)解:依题意,得,
整理,得,
解得,.
当时,;当时,.
答:售卖区的长为,宽为或长为,宽为.
(3)解:结合(2)可得:当时,不能围成售卖区,题目无解;
当时,围成的售卖区只有一种围法,题目只有一个解;
当时,围成的售卖区有两种围法,题目有两个解.
综上所述,当时,围成的售卖区只有一种围法,
即的取值范围是.
8.水渠的宽度为
【分析】本题考查一元二次方程的应用,根据耕地总面积列出方程求解即可.正确找到等量关系列出方程是解题关键.
【详解】解:设水渠的宽度为,
依题意,得:,
解得:(,不符合题意,舍去),,
答:水渠的宽度为.
9.(1)8,
(2)过道的宽度为 2 米
【分析】本题考查了一元二次方程的应用,一元一次方程的应用.熟练掌握一元二次方程的应用,一元一次方程的应用是解题的关键.
(1)设正方形的边长为米,则,依题意得,,计算求解,然后作答即可;
(2)设过道的宽度为米,依题意得,,计算求出满足要求的解即可.
【详解】(1)解:设正方形的边长为米,则,
∵长与宽之比为,
∴,
解得,,
∴,,
故答案为:8,.
(2)解:设过道的宽度为米,
依题意得,,
解得,或(舍去),
∴过道的宽度为2米.
10.(1)垂直于墙的一边为,则平行于墙的一边为时,养鸡场的面积为
(2)不能,见解析
【分析】此题主要考查了一元二次方程的应用;
(1)首先设垂直于墙的一边为,则平行于墙的一边为,然后根据矩形的面积长宽,用未知数表示出鸡场的面积,根据面积为,可得方程,解方程即可;
(2)要求鸡场的面积能否达到,只需让鸡场的面积先等于,然后看得出的一元二次方程有没有解,如果有就证明可以达到,如果方程无实数根,说明不能达到.
【详解】(1)解:设垂直于墙的一边为,则平行于墙的一边为,
根据题意得:,
解得,
答:垂直于墙的一边为,则平行于墙的一边为时,养鸡场的面积为;
(2)解:不能,理由如下:
根据题意得:,
整理得,,
,
∴方程无实数根,
∴不能使鸡场的面积能达到.
11.(1)
(2)2
【分析】本题考查了一元二次方程的应用,解题的关键是∶
(1)利用画框的长减去三个纸卡的宽,再除以2求解即可;
(2)根据空白处的面积为列方程求解即可.
【详解】(1)解:根据题意得,
故答案为:;
(2)解:根据题意,得,
解得,,
即当时,空白处的面积为.
12.(1)
(2)销售单价定为50元时所获利润为9000元
【分析】本题主要考查一元二次方程的实际应用,关键是根据题意得到一元二次方程,然后进行求解即可.
(1)由彩色图案的宽度为,则除去彩色图案的剩余部分可合成长为,宽为的长方形,根据长方形的面积公式得;
(2)设每件工艺品的售价为元,则每件的销售利润为元,每天可售出件.根据单利润乘以数量等于列一元二次方程求解即可.
【详解】(1)解:由题意得,
故答案为:;
(2)解:设每件工艺品的售价为元,则每件的销售利润为元,每天可售出件.
根据题意,得,
整理,得,解得(不符合题意,舍去),
当该公司每天把销售单价定为元时所获利润为元.
13.(1),
(2)5
(3)
【分析】本题主要考查了一元二次方程的应用,长方体的平面展开图等知识点,
(1)根据长两个小正方形的长,宽两个小正方形的宽即可得到答案;
(2)根据面积=长×宽,列出关于x的一元二次方程,解之即可;
(3)利用长方体的体积公式计算即可;
根据题意找出等量关系,列出方程是解决此题的关键.
【详解】(1)根据题意得:长:,宽:;
故答案为:,;
(2)根据题意得:
整理得:
解得:(舍去),,
∴小正方形边长为x的值为5;
(3)∵,
∴,,
∴根据题意得:(2)中长方体纸盒的容积为:.
14.(1)长为;
(2)不能,理由见解析.
【分析】()设,则,列出方程即可求解;
()设,则,列出方程然后判断有无实数根即可求解;
此题考查了一元二次方程的应用,正确理解题意、准确列出一元二次方程是解题的关键.
【详解】(1)解:设,则,
则 ,
整理得,
解得,
由题意得:,解得,
∴不合题意,舍去,
答:长为;
(2)解:设,则,
则 ,
整理得,
,
∴方程无实数根,
∴不能围成面积为平方米的矩形.
15.(1)新的矩形场地的长为,宽为;
(2)票价应定为40元/人
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)设场地的长、宽增加,则新的矩形场地的长为,宽为,根据扩充后的矩形场地面积为,可列出关于的一元二次方程,解之可得出的值,再将其符合题意的值代入及中,即可求出结论;
(2)设票价应定为元人,则游客数为每天人,利用儿童乐园日营业额票价日游客数,可列出关于的一元二次方程,解之即可得出结论.
【详解】(1)解:设场地的长、宽增加,则新的矩形场地的长为,宽为,
根据题意得:,
整理得:,
解得:,(不符合题意,舍去),
,
.
答:新的矩形场地的长为,宽为;
(2)解:设票价应定为元人,则游客数为每天人,
根据题意得:,
整理得:,
解得:.
答:票价应定为40元人.
16.(1)米
(2).
【分析】本题主要考查一元二次方程的应用、一元二次方程的求解及一元一次不等组的求解;根据实际情境确定变量的取值范围,对方程解作合理取舍是解题的关键.
(1)由得,再由即可得出答案;
(2)根据矩形的面积等于长宽建立方程,求解并检验即可.
【详解】(1)解:如图,
∴
∴米;
(2)解:由题意知,
解得,,
又∵,且
∴,
∴.
17.(1)长为13米,则宽为10米
(2)20米
【分析】此题主要考查了一元二次方程的应用,关键是弄懂题意,找出题目中的等量关系,要注意判断所求的解是否符合题意,舍去不合题意的解.
(1)设长方形的长为,则宽为米,而仓库的面积为,由此即可列出方程,解方程就可以解决问题;
(2)根据长方形的长宽列出不等式,并解答.
【详解】(1)设长方形的长为,则宽为米,
由题意,得
解得或
当时,显然,不符合题意,舍去
所以.
答:长方形的长为13米,则宽为10米;
(2)解:∵宽为10米米,
此时不符合题意.
当长为20米时,宽为6.5米米,
米,
∴墙长至少要20米.
18.(1)10;
(2)能,1米.
【分析】本题考查了一元一次不等式的应用,一元二次方程的应用,找出不等关系式和等量关系式是解题的关键.
(1)设与墙垂直的一面为米,另一面则为米,然后利用这堵墙的长度为不超过米,列出不等式求解即可;
(2)设小路的宽为a米,两边的长分别为米,米,列出方程求解即可求解.
【详解】(1)解:设与墙垂直的一面为米,另一面则为米,
根据题意得:.
解得:,
答:长方形车棚与墙垂直的一面至少米;
(2)解:设小路的宽为a米,
根据题意得,.
整理得;,
解得:(舍去),.
答:小路的宽为1米.
19.(1);
(2)不可以,理由见解析
【分析】此题主要考查了一元二次方程的应用,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
(1)根据矩形的周长公式求得边的长度;然后由矩形的面积公式求得矩形的面积;
(2)根据矩形的面积公式得到关于的方程,通过解方程求得答案.
【详解】(1)解:∵用一条长的绳子围成矩形,设边的长为
∴,,,
∴,
∴边的长为:,
矩形的面积为:;
故答案为:;;
(2)解:不可以,理由如下:
若矩形的面积是,则,
即,
,
这个方程无解,
矩形的面积不可以是.
20.(1)①该采茶基地的宽为20米,长为30米;②该采茶基地需要100米长的篱笆
(2)小路的宽度为1米
【分析】本题考查了一元二次方程的应用,正确理解题意是解题的关键.
(1)①设采茶基地的宽为米,则长为米,根据面积为600平方米列方程,解方程即得答案;②根据长方形的周长,即得答案;
(2)设小路的宽度为米,根据鲜花的种植面积为486平方米列出方程,解方程即得答案.
【详解】(1)解:①设采茶基地的宽为米,则长为米,
根据题意得,
整理得,
解得,(不合题意,舍去),
,
答:该采茶基地的宽为20米,长为30米.
②根据题意得米,
答:该采茶基地需要100米长的篱笆.
(2)解:设小路的宽度为米,
则,
整理得,
解得,(不合题意,舍去),
答:小路的宽度为1米.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
专题 05:一元二次方程的应用(与图形相关的问题)--2024-2025年人教版九年级上册数学期末专题提升训练
1.如图,老李想用长为的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈,并在边上留一个宽的门(建在处,另用其他材料).设的长是.
AI
(1)填空:______;
(2)若羊圈的面积是,求的值.
2.某社区为了解决停车难的问题,利用一块矩形空地建了一个小型停车场,其布局如图所示.已知,,阴影部分设计为停车位,其余部分均为宽度为米的道路.已知停车位的面积(即阴影面积)为.
(1)求道路的宽是多少米?
(2)该停车场共有车位70个,据调查分析,当每个车位的月租金为300元时,可全部租出;若每个车位的月租金每上涨5元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为21120元,同时尽可能让利于居民?
3.月日中华人民共和国国家勋章和国家荣誉称号颁授仪式在人民大会堂隆重举行,我国小麦远缘杂交育种奠基人和农业发展战略专家李振声,在祖国西北耕耘载,培育推广抗病、高产的远缘杂交小麦,被授予“共和国勋章”.某校八年级学生利用课余时间进行劳动实践,准备种植远缘杂交小麦,试验田一边靠学校的墙(墙的最大可用长度为),其他边用长为的篱笆(篱笆正好全部用完,且不考虑接头的部分)围成中间隔有一道篱笆的长方形,在试验田的前端设计了两个宽的小门,供同学们进出.设试验田的一边的长为.
(1)求当为何值时,围成的试验田面积为;
(2)能围成面积为的试验田吗?请通过计算说明理由.
4.素材1:图是拟建中的一个温室平面设计图纸,图纸上1个单位长度代表实际距离1米,温室是一个矩形,其周长为120,准备在它的四周铺设道路,左右两条纵向道路的宽度都为1,上边横向道路的宽度为1,下边横向道路的宽度为3,中间部分(阴影部分)种植草莓,种植面积为720.
素材2:道路的路面造价是70元平方米;经市场调查,草莓培育一年可产果,已知每平方米的草莓销售平均利润为100元;其余费用为3万元.
任务1:(1)实际中温室的长不能大于35米,通过计算说明拟建的温室是否达标;
任务2:(2)求经过1年后,温室年净利润为多少?(净利润=草莓销售的总利润-路面造价费用-其余费用)
5.某扶贫单位为了提高贫困户的经济收入,购买了的铁栅栏,准备用这些铁栅栏为贫困户靠墙(墙长)围建一个中间带有铁栅栏的矩形养鸡场(如图所示).
(1)若要建的矩形养鸡场面积为,求鸡场的长和宽;
(2)该扶贫单位想要建一个的矩形养鸡场,这一想法能实现吗?请说明理由.
6.春回大地,万物复苏,又是一年花季到.某花圃基地计划将如图所示的一块长,宽的矩形空地划分成五块小矩形区域.其中一块正方形空地为育苗区,另一块空地为活动区,其余空地为种植区,分别种植A,B,C三种花卉.活动区一边与育苗区等宽,另一边长是.A,B,C三种花卉每平方米的产值分别是2百元、3百元、4百元.
(1)设育苗区的边长为,用含x的代数式表示下列各量:花卉A的种植面积是______,花卉B的种植面积是______,花卉C的种植面积是______,
(2)育苗区的边长为多少时,A,B两种花卉的总产值相等?
7.自今年4月底以来,惠水县好花红乡村旅游区的桔香花海山体公园成为了网红打卡点.现在公园管理者要修建一个面积为的长方形精品花售卖区(如图).为了节省材料,售卖区的一边利用原有的一道墙,另三边用总长为的栅栏围成,边留有宽的门.
(1)若售卖区垂直于墙的边的长为,则边的长为 .
(2)若墙足够长,则售卖区的长和宽各为多少米?
(3)当围成的售卖区只有一种围法时,求墙长a的取值范围.
8.如图,有一块长为,宽为的矩形耕地,为方便灌溉,现需在耕地上挖两条宽度相等的水渠,水渠把耕地分成面积均为的个矩形小块,求水渠的宽度.
9.同学们开展的综合实践活动中取得了系列丰硕的成果,需要推广宣传.原计划使用一块正方形场地布展,后经过研究,发现长与宽之比为的长方形场地展览效果更好,因此需要把长增加6米,宽增加2米(如图1).
(1)直接写出长方形区域的宽是_______m,长是_______m.
(2)现计划将长方形区域按图2的方式进行划分,展示四各小组的项目成果,在各展区之间留宽度相等的过道.如果各展区的总面积为,求过道的宽度.
10.某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙的长度不限),另外三边用木栏围成,木栏长.
(1)怎样围成一个面积为的矩形场地?
(2)能围成面积能为的矩形场地吗?若不能,说明理由?
11.宫格画(图1)因其独特的艺术性近年来受到年轻人的追捧.如图2,小欣利用宽度相等的纸卡(灰色阴影部分)制作了一个长为,宽为的宫格画画框,空白处的宽度相同,设纸卡的宽为.
(1)图2中空白处的宽度_________.(用含x的式子表示)
(2)若图2中空白处的面积为,求x的值.
12.某公司展销如图所示的长方形工艺品,该工艺品长,宽,中间镶有宽度相同的三条彩色图案.
(1)若除去彩色图案后剩余的面积为,设彩色图案的宽度为,则可列方程为______;(要求用原数列方程,不要求化简)
(2)已知该工艺品的成本是元/件,物价局规定销售单价在元至元的范围内,如果以单价元/件销售,那么每天可售出件,另外每天除工艺品的成本外所需支付的各种费用是元,根据销售经验,如果将销售单价每上涨元,每天就少售出件.请问该公司每天把销售单价定为多少元时所获利润为元?
13.综合与实践
如图1,有一张长,宽的长方形硬纸片,截去四个大小相同小正方形之后,折成如图2所示的长方体形的无盖纸盒,设截取的小正方形边长为.
(1)用含有x的代数式分别表示无盖纸盒底面的长(________),宽(________);
(2)若纸盒的底面积为,求小正方形边长为x的值;
(3)求出(2)中长方体纸盒的容积.
14.如图,有长为的篱笆,一面利用墙(墙长为),围成如图所示的矩形花圃.
(1)如果要围成面积为的花圃,那么的长为多少米?
(2)能否围成面积为的花圃?若能,求出的长;若不能,请说明理由.
15.如图,某儿童乐园的场地是长宽分别为,的矩形.儿童乐园进行改造升级,场地也进行扩充,将场地的长、宽增加相同的长度后,新场地仍是一个矩形.
(1)若扩充后的矩形场地面积为,求新的矩形场地的长与宽;
(2)儿童乐园改造升级后,经过调查发现,票价30元/人时游客数为每天500人,票价每提高1元,则游客减少10人,要使得儿童乐园日营业额达到1.6万元,票价应定为多少元?
16.如图,某农场有两堵互相垂直的墙,长度分别为27米和15米,该农场打算借这两堵墙建一个长方形饲养场,其中和两边借助墙体且不超出墙体,其余部分用总长45米的木栏围成,中间预留1米宽的通道,在和边上各留1米宽的门、设长x米,
(1)求的长度(用含x的代数式表示).
(2)若饲养场的面积为180平方米,求x的值.
17.如图,现准备用32米长的木板建有关面积为130平方米的长方形仓库,仓库的一边靠墙,并在与墙垂直的一边开一道1米宽的小门.
(1)如果墙长15米,求仓库的长和宽;
(2)如果墙长a米,在离开墙9米开外仓库一侧修条小路,那么墙长至少要多少米?
18.学校计划利用一片空地建一个长方形自行车车棚,其中一面靠墙,墙的长度为8米.在与墙平行的一面开一个2米宽的门,已知现有的木板材料可修建的总长为26米,且全部用于除墙外其余三面外墙的修建.
(1)长方形车棚与墙垂直的一面至少为__________米;
(2)如图,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路(如图中阴影),若车棚与墙垂直的一面长按(1)中的最小长度,则停放电动车的区域面积能否达到54平方米,若能,此时小路的宽度是多少米?若不能,请说明理由.
19.如图,用一条长的绳子围成矩形,设边的长为.
(1)边的长为______,矩形的面积为______(均用含的代数式表示);
(2)矩形的面积是否可以是?请给出你的结论,并用所学的方程或者函数知识说明理由.
20.山西槐米茶,口感清香,冲泡汤色亮黄,味道醇厚,具有清血凉血,抗菌消炎等功效.
(1)如图1,太原市某茶庄种植槐米茶,由于规模不断扩大,现计划开阔一块面积为600平方米的长方形采茶基地,已知该采茶基地的长比宽多10米.
①分别求该采茶基地的长和宽;
②若要在采茶基地的四周围上篱笆,问需要多长的篱笆?
(2)如图2,该茶庄开设了一片观光园区,园区内原有一块长方形空地,该空地与(1)中的采茶基地大小、形状相同,后计划在此区域栽种鲜花(阴影部分)并铺设如图所示的宽度相同的小路(空白部分)供游客观光,若鲜花的种植面积为486平方米,求小路的宽度.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1);
(2)或.
【分析】本题考查了一元二次方程的应用及列代数式,解题的关键是要理解题意,能正确列出方程.
(1)根据栅栏总长列式即可;
(2)利用矩形面积公式即可求解.
【详解】(1)解:设的长是,则
,
故答案为:;
(2)解:根据题意:,
整理得:,
解得:,,
∴的值为或.
2.(1)道路的宽是4米
(2)每个车位的月租金上涨20元时,停车场的月租金收入为21120元
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)道路的宽为米,根据铺花砖的面积(即阴影面积)为,结合其布局图,列出一元二次方程,解方程取符合题意的值即可;
(2)设每个车位的月租金上涨元时,停车场的月租金收入为21120元,根据“该停车场共有车位70个,据调查分析,当每个车位的月租金为300元时,可全部租出;若每个车位的月租金每上涨5元,就会少租出1个车位”,列出一元二次方程,解方程取尽可能让利于居民的值即可.
【详解】(1)解:道路的宽为米,
由题意得:,
整理得:,
解得:(不合题意,舍去),,
答:道路的宽是4米;
(2)解:设每个车位的月租金上涨元时,停车场的月租金收入为21120元,
由题意得:,
整理得:,
解得:,
∵尽可能让利于居民,
,
答:每个车位的月租金上涨20元时,停车场的月租金收入为21120元.
3.(1)当为时,围成的试验田面积为
(2)不能围成面积为的试验田,理由见解析
【分析】本题考查了一元二次方程的应用,解题的关键是理解题意,正确找出等量关系.
(1)设试验田的一边的长为,则,根据长方形的面积列方程即可求解;
(2)根据题意列出方程,再利用一元二次方程根的判别式即可判断.
【详解】(1)解:设试验田的一边的长为,则,
根据题意可得:,
解得:或,
当时,,不合题意,舍去,
当为时,围成的试验田面积为;
(2)不能围成面积为的试验田,理由如下:
根据题意可得:,
整理得:,
,
该方程无实数根,
即不能围成面积为的试验田.
4.任务:(1)温室达标,详见解析;
任务:(2)元
【分析】本题考查了一元二次方程的应用,根据题意正确列出一元二次方程是解题的关键.
(1)设,则,,,由题意得,,解方程即可得到答案;
(2)根据题意正确列算式,求解即可.
【详解】解:任务:(1)设,
则,,,
根据题意得,,即,
解得,
∵,
∴,
∴,
∵,
∴温室达标;
任务:(2)由(1)知,,
∴温室的面积为,
∴道路面积为,
∴道路总造价为,
∴草莓的总利润为,
∴净利润为
答:温室年净利润为元 .
5.(1)长和宽分别为与
(2)不能,理由见解析
【分析】本题考查一元二次方程的实际应用,能根据几何图形正确列出方程是解题的关键.
(1)设,则,根据面积列出方程,求解验根即可;
(2)设,则,根据面积列出方程,利用根的判别式判断方程是否有解,并是否符合题意,即可解决.
【详解】(1)解:设,
∵铁栅栏总长为,
∴,
由题意得:,
整理得:,
解得:,,
当时,,不符合题意;
当时,,符合题意;
答:鸡场的长和宽分别为与;
(2)解:设,则,
由题意得:,
整理得:,
∵,
∴方程无解,
故这一想法不能实现.
6.(1);;
(2)
【分析】本题考查的是列代数式,整式乘法的应用,一元二次方程的应用,根据题意正确列出代数式是解题的关键.
(1)根据题意可知:花卉A的种植面积是:;花卉B的种植面积是:;花卉C的种植面积是:;
(2)先计算出A,B两种种花卉的总产值分别是百元、百元,根据A,B两种花卉的总产值相等,可得,求解即可.
【详解】(1)解:根据题意可知:
花卉A的种植面积是:;
花卉B的种植面积是;
花卉C的种植面积是:;
故答案为:;;.
(2)解:两种花卉每平方米的产值分别是2百元、3百元,
,B两种花卉的总产值分别百元、百元,
,B两种花卉的总产值相等,
,
解得:(舍去)或,
∴育苗区的边长为时,A,B两种花卉的总产值相等.
7.(1)
(2)售卖区的长为,宽为或长为,宽为.
(3).
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)设垂直于墙的边长为,可得平行于墙的边长为,整理即可;
(2)根据矩形的面积公式结合养鸡场的面积为,列出一元二次方程,解之即可得出结论;
(3)根据(1)的结论可分、及三种情况,找出题目解的个数,即可得出结论.
【详解】(1)解:∵售卖区垂直于墙的边的长为,
∴边的长为.
(2)解:依题意,得,
整理,得,
解得,.
当时,;当时,.
答:售卖区的长为,宽为或长为,宽为.
(3)解:结合(2)可得:当时,不能围成售卖区,题目无解;
当时,围成的售卖区只有一种围法,题目只有一个解;
当时,围成的售卖区有两种围法,题目有两个解.
综上所述,当时,围成的售卖区只有一种围法,
即的取值范围是.
8.水渠的宽度为
【分析】本题考查一元二次方程的应用,根据耕地总面积列出方程求解即可.正确找到等量关系列出方程是解题关键.
【详解】解:设水渠的宽度为,
依题意,得:,
解得:(,不符合题意,舍去),,
答:水渠的宽度为.
9.(1)8,
(2)过道的宽度为 2 米
【分析】本题考查了一元二次方程的应用,一元一次方程的应用.熟练掌握一元二次方程的应用,一元一次方程的应用是解题的关键.
(1)设正方形的边长为米,则,依题意得,,计算求解,然后作答即可;
(2)设过道的宽度为米,依题意得,,计算求出满足要求的解即可.
【详解】(1)解:设正方形的边长为米,则,
∵长与宽之比为,
∴,
解得,,
∴,,
故答案为:8,.
(2)解:设过道的宽度为米,
依题意得,,
解得,或(舍去),
∴过道的宽度为2米.
10.(1)垂直于墙的一边为,则平行于墙的一边为时,养鸡场的面积为
(2)不能,见解析
【分析】此题主要考查了一元二次方程的应用;
(1)首先设垂直于墙的一边为,则平行于墙的一边为,然后根据矩形的面积长宽,用未知数表示出鸡场的面积,根据面积为,可得方程,解方程即可;
(2)要求鸡场的面积能否达到,只需让鸡场的面积先等于,然后看得出的一元二次方程有没有解,如果有就证明可以达到,如果方程无实数根,说明不能达到.
【详解】(1)解:设垂直于墙的一边为,则平行于墙的一边为,
根据题意得:,
解得,
答:垂直于墙的一边为,则平行于墙的一边为时,养鸡场的面积为;
(2)解:不能,理由如下:
根据题意得:,
整理得,,
,
∴方程无实数根,
∴不能使鸡场的面积能达到.
11.(1)
(2)2
【分析】本题考查了一元二次方程的应用,解题的关键是∶
(1)利用画框的长减去三个纸卡的宽,再除以2求解即可;
(2)根据空白处的面积为列方程求解即可.
【详解】(1)解:根据题意得,
故答案为:;
(2)解:根据题意,得,
解得,,
即当时,空白处的面积为.
12.(1)
(2)销售单价定为50元时所获利润为9000元
【分析】本题主要考查一元二次方程的实际应用,关键是根据题意得到一元二次方程,然后进行求解即可.
(1)由彩色图案的宽度为,则除去彩色图案的剩余部分可合成长为,宽为的长方形,根据长方形的面积公式得;
(2)设每件工艺品的售价为元,则每件的销售利润为元,每天可售出件.根据单利润乘以数量等于列一元二次方程求解即可.
【详解】(1)解:由题意得,
故答案为:;
(2)解:设每件工艺品的售价为元,则每件的销售利润为元,每天可售出件.
根据题意,得,
整理,得,解得(不符合题意,舍去),
当该公司每天把销售单价定为元时所获利润为元.
13.(1),
(2)5
(3)
【分析】本题主要考查了一元二次方程的应用,长方体的平面展开图等知识点,
(1)根据长两个小正方形的长,宽两个小正方形的宽即可得到答案;
(2)根据面积=长×宽,列出关于x的一元二次方程,解之即可;
(3)利用长方体的体积公式计算即可;
根据题意找出等量关系,列出方程是解决此题的关键.
【详解】(1)根据题意得:长:,宽:;
故答案为:,;
(2)根据题意得:
整理得:
解得:(舍去),,
∴小正方形边长为x的值为5;
(3)∵,
∴,,
∴根据题意得:(2)中长方体纸盒的容积为:.
14.(1)长为;
(2)不能,理由见解析.
【分析】()设,则,列出方程即可求解;
()设,则,列出方程然后判断有无实数根即可求解;
此题考查了一元二次方程的应用,正确理解题意、准确列出一元二次方程是解题的关键.
【详解】(1)解:设,则,
则 ,
整理得,
解得,
由题意得:,解得,
∴不合题意,舍去,
答:长为;
(2)解:设,则,
则 ,
整理得,
,
∴方程无实数根,
∴不能围成面积为平方米的矩形.
15.(1)新的矩形场地的长为,宽为;
(2)票价应定为40元/人
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)设场地的长、宽增加,则新的矩形场地的长为,宽为,根据扩充后的矩形场地面积为,可列出关于的一元二次方程,解之可得出的值,再将其符合题意的值代入及中,即可求出结论;
(2)设票价应定为元人,则游客数为每天人,利用儿童乐园日营业额票价日游客数,可列出关于的一元二次方程,解之即可得出结论.
【详解】(1)解:设场地的长、宽增加,则新的矩形场地的长为,宽为,
根据题意得:,
整理得:,
解得:,(不符合题意,舍去),
,
.
答:新的矩形场地的长为,宽为;
(2)解:设票价应定为元人,则游客数为每天人,
根据题意得:,
整理得:,
解得:.
答:票价应定为40元人.
16.(1)米
(2).
【分析】本题主要考查一元二次方程的应用、一元二次方程的求解及一元一次不等组的求解;根据实际情境确定变量的取值范围,对方程解作合理取舍是解题的关键.
(1)由得,再由即可得出答案;
(2)根据矩形的面积等于长宽建立方程,求解并检验即可.
【详解】(1)解:如图,
∴
∴米;
(2)解:由题意知,
解得,,
又∵,且
∴,
∴.
17.(1)长为13米,则宽为10米
(2)20米
【分析】此题主要考查了一元二次方程的应用,关键是弄懂题意,找出题目中的等量关系,要注意判断所求的解是否符合题意,舍去不合题意的解.
(1)设长方形的长为,则宽为米,而仓库的面积为,由此即可列出方程,解方程就可以解决问题;
(2)根据长方形的长宽列出不等式,并解答.
【详解】(1)设长方形的长为,则宽为米,
由题意,得
解得或
当时,显然,不符合题意,舍去
所以.
答:长方形的长为13米,则宽为10米;
(2)解:∵宽为10米米,
此时不符合题意.
当长为20米时,宽为6.5米米,
米,
∴墙长至少要20米.
18.(1)10;
(2)能,1米.
【分析】本题考查了一元一次不等式的应用,一元二次方程的应用,找出不等关系式和等量关系式是解题的关键.
(1)设与墙垂直的一面为米,另一面则为米,然后利用这堵墙的长度为不超过米,列出不等式求解即可;
(2)设小路的宽为a米,两边的长分别为米,米,列出方程求解即可求解.
【详解】(1)解:设与墙垂直的一面为米,另一面则为米,
根据题意得:.
解得:,
答:长方形车棚与墙垂直的一面至少米;
(2)解:设小路的宽为a米,
根据题意得,.
整理得;,
解得:(舍去),.
答:小路的宽为1米.
19.(1);
(2)不可以,理由见解析
【分析】此题主要考查了一元二次方程的应用,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
(1)根据矩形的周长公式求得边的长度;然后由矩形的面积公式求得矩形的面积;
(2)根据矩形的面积公式得到关于的方程,通过解方程求得答案.
【详解】(1)解:∵用一条长的绳子围成矩形,设边的长为
∴,,,
∴,
∴边的长为:,
矩形的面积为:;
故答案为:;;
(2)解:不可以,理由如下:
若矩形的面积是,则,
即,
,
这个方程无解,
矩形的面积不可以是.
20.(1)①该采茶基地的宽为20米,长为30米;②该采茶基地需要100米长的篱笆
(2)小路的宽度为1米
【分析】本题考查了一元二次方程的应用,正确理解题意是解题的关键.
(1)①设采茶基地的宽为米,则长为米,根据面积为600平方米列方程,解方程即得答案;②根据长方形的周长,即得答案;
(2)设小路的宽度为米,根据鲜花的种植面积为486平方米列出方程,解方程即得答案.
【详解】(1)解:①设采茶基地的宽为米,则长为米,
根据题意得,
整理得,
解得,(不合题意,舍去),
,
答:该采茶基地的宽为20米,长为30米.
②根据题意得米,
答:该采茶基地需要100米长的篱笆.
(2)解:设小路的宽度为米,
则,
整理得,
解得,(不合题意,舍去),
答:小路的宽度为1米.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
