2024-2025年人教版九年级上册数学期末专题提升训练08:一元二次方程的应用(动态几何问题)(含解析)
文档属性
| 名称 | 2024-2025年人教版九年级上册数学期末专题提升训练08:一元二次方程的应用(动态几何问题)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-07 14:54:37 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
专题 08:一元二次方程的应用(动态几何问题)--2024-2025年人教版九年级上册数学期末专题提升训练
一、单选题
1.如图,在矩形中,,,动点,同时出发,点从点出发以的速度向点移动,一直到达点为止,点从点出发以的速度向点移动,则当点和点的距离是时,,两点出发了( )
A. B.s或 C.s或 D.s
2.如图,中,,,,点P从点B出发向终点C以每秒1个单位长度的速度移动,点Q从点C出发向终点A以每秒2个单位长度的速度移动,P,Q两点同时出发,其中一点先到达终点时P,Q两点同时停止移动.则当的面积等于8时,经过了( )
A.1秒 B.6秒 C.8秒 D.1秒或8秒
3.如图所示,在中,,,,点P以的速度从点A开始沿边向点B移动,点Q以的速度从点B开始沿边向点C移动,且点P,Q分别从点A,B同时出发.若有一点到达目的地,则另一点同时停止运动.要使P,Q两点之间的距离等于,则需要经过( )
A. B. C. D.或
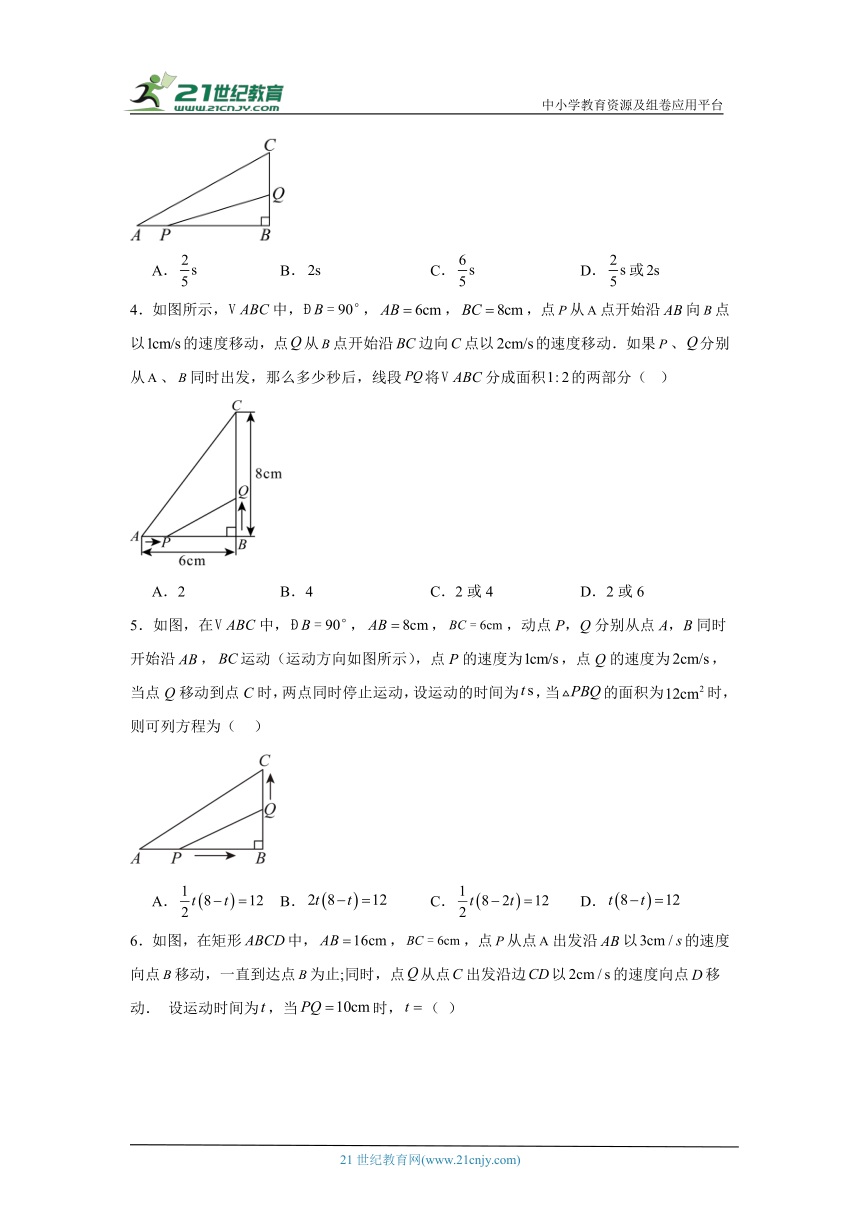
4.如图所示,中,,,,点从点开始沿向点以的速度移动,点从点开始沿边向点以的速度移动.如果、分别从、同时出发,那么多少秒后,线段将分成面积的两部分( )
A.2 B.4 C.2或4 D.2或6
5.如图,在中,,,,动点P,Q分别从点A,B同时开始沿,运动(运动方向如图所示),点P的速度为,点Q的速度为,当点Q移动到点C时,两点同时停止运动,设运动的时间为,当的面积为时,则可列方程为( )
A. B. C. D.
6.如图,在矩形中,,,点从点出发沿以的速度向点移动,一直到达点为止;同时,点从点出发沿边以的速度向点移动. 设运动时间为,当时,( )
A. B.或4 C.或 D.
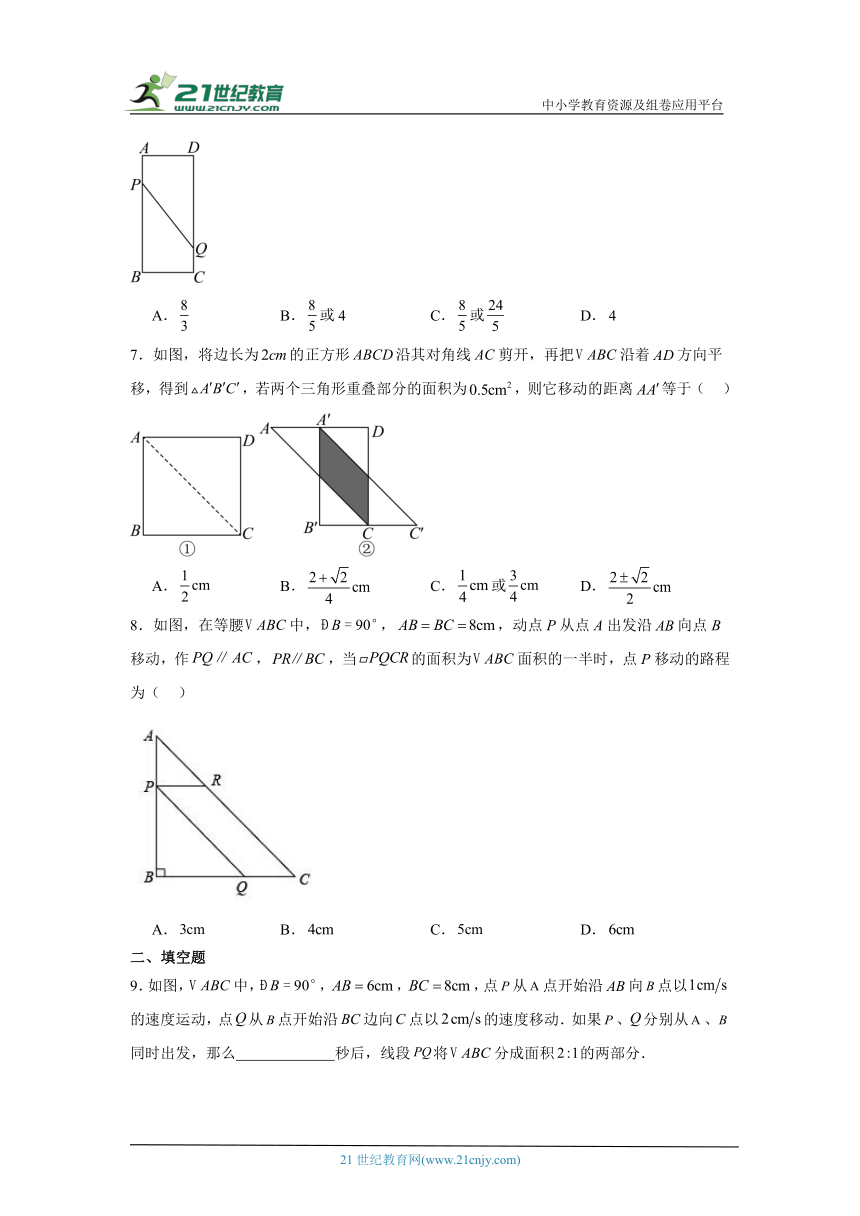
7.如图,将边长为的正方形沿其对角线剪开,再把沿着方向平移,得到,若两个三角形重叠部分的面积为,则它移动的距离等于( )
A. B. C.或 D.
8.如图,在等腰中,,,动点P从点A出发沿向点B移动,作,,当的面积为面积的一半时,点P移动的路程为( )
A. B. C. D.
二、填空题
9.如图,中,,,,点从点开始沿向点以的速度运动,点从点开始沿边向点以的速度移动.如果、分别从、同时出发,那么 秒后,线段将分成面积的两部分.
10.如图,在中,,,,点D从点C开始沿边运动,速度为,与此同时,点E从点B开始沿边运动,速度为,当点E到达点C时,点D同时停止运动,连接,设运动时间为,的面积为S.当时, s.
11.如图,在中,,,,是中点,动点从点出发沿边向点以的速度移动,同时动点从点出发沿边向点以的速度移动,当运动到点时两点同时停止运动,连接、,为 时的面积为.
12.如图,在中,,动点P从点C出发,沿方向运动,动点Q从点B出发,沿方向运动,如果点P,Q的运动速度均为.那么运动 秒时,它们相距?
13.如图,在边长为正方形中,点P从点A开始沿边向点B以的速度移动,点Q从点B开始沿和边向D点以的速度移动,如果点P、Q分别从A、B同时出发,其中一点到终点,另一点也随之停止.过了 秒钟后,的面积等于.
14.如图,菱形中,,交于,,,动点从出发沿方向以每秒匀速直线运动到,动点从出发沿方向以每秒匀速直线运动到,若,同时出发,问出发后 s时,的面积为菱形面积的?
15.如图,在中,,,点从点出发,沿射线方向以的速度移动,点从点出发,沿射线方向以的速度移动,如果、两点同时出发,问:经过 秒后的面积等于.
16.如图,在四边形中,,,,,.动点P从点D出发,沿射线的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t秒,当 时,以B,P,Q三点为顶点的三角形是等腰三角形.
三、解答题
17.如图,在中,,,,点从点开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动.若,两点同时出发,当点运动到点时,,两点同时停止运动.求:
(1)经过几秒后,的长度等于?
(2)请直接写出的面积能否等于?
18.在长方形中,,,点从点开始沿边向终点以的速度移动,与此同时,点从点开始沿向终点以的速度移动,如果,分别从,同时出发,当点运动到点时,两点停止运动.设运动时间为.
(1)填空:________,_______(用含的代数式表示);
(2)当为何值时,的长为?
(3)是否存在的值,使得五边形的面积等于?若存在,请求出此时的值,若不存在,请说明理由.
19.在矩形中,,,点从出发,沿以的速度向点B匀速移动,同时点从点出发,沿以的速度向点匀速移动.设运动的时间为.
(1)______,______;
(2)为何值时,的面积等于?
20.如图,菱形中, 交于点 O, ,动点 M 从 A 点出发沿方向以匀速直线运动到 C 点,动点 N 从 B 点出发沿方向以匀速直线运动到 D 点.若 M,N 同时出发,设运动时间为 t 秒:
(1)当时, , .(用 t 表示)
(2)当秒时, 的面积为多少?
(3)点 M 到达点 C 后立即原路返回,速度保持不变,直到点 N 到达 D 后同时停止运动,那么在整个移 动过程中,是否存在某一时刻,使得的面积为?若存在,求出运动时间;若不存在,请说 明理由.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
题号 1 2 3 4 5 6 7 8
答案 B A A C D C D B
1.B
【分析】本题考查了一元二次方程的应用,勾股定理,矩形的性质,利用勾股定理,找出等量关系是解题的关键.过点作于点,则四边形是矩形,当运动时间为秒时,,,则,根据题意得:,即,即可求解.
【详解】解:如图,过点作于点,则四边形是矩形,
(秒),
当运动时间为秒时,,,
,
根据题意得:,
即,
整理得:,
解得:,,
当点和点的距离是时,、两点出发了秒或秒.
故选:B.
2.A
【分析】本题考查了一元二次方程的应用,理解题意,找准等量关系,正确列出一元二次方程是解此题的关键.
设经过了秒,的面积等于8,用含的代数式表示和,根据三角形的面积公式建立方程,求解即可.
【详解】解:设经过了秒,的面积等于8,则
,
解得:,,
∵点Q从点C到点A需要的时间是:(秒),
∴,不合题意,应舍去,
因此,则当的面积等于8时,经过了1秒.
故答案为:A.
3.A
【分析】本题主要考查勾股定理以及一元二次方程的应用.根据勾股定理列出方程是解题的关键.
设经过,P、Q之间的距离等于,先用含x的代数式分别表示和的长度,进一步利用勾股定理建立方程求得答案即可.
【详解】设后P、Q之间的距离等于,
∵,
∴,
∵,
∴,
解得,(不合题意,舍去),
∴,
需要经过.
故选:A.
4.C
【分析】本题考查了一元二次方程的应用,理解题意,找出等量关系正确列方程是解题关键.
设运动时间为,根据题意可得,,再根据三角形面积公式分两种情况求解即可.
【详解】解:设运动时间为,则,
,
,
∵线段将分成面积的两部分,
或,
或,
整理得:或(无实数解).
解得:,
即线段将分成面积的两部分,运动时间为2或4秒.
故选:C.
5.D
【分析】本题考查一元二次方程在几何图形中的应用,当运动时,,,根据“的面积为”即可列出方程.
【详解】当运动时,,,,
∵,
∴,
即.
故选:D
6.C
【点评】此题考查了一元二次方程的运用.利用作垂线,构造直角三角形,运用勾股定理列方程是解题关键.
作,垂足为H,设运动时间为t秒,用t表示线段长,用勾股定理列方程求解.
【详解】解:设P,Q两点从出发经过t秒时,点P,Q间的距离是,
作,垂足为H,
则,,.
,
可得:,
解得,.
答:P,Q两点从出发经过或秒时,点P,Q间的距离是.
故答案为:C.
7.D
【分析】根据平移的性质,结合阴影部分是平行四边形,与都是等腰直角三角形,则若设,则阴影部分的底长为x,高,根据平行四边形的面积公式即可列出方程求解.
【详解】解:设交于H,交于点G,
由平移的性质知,,
∴四边形是平行四边形,
∵由正方形的性质可得:,,
∴是等腰直角三角形,
同理,也是等腰直角三角形,
设,则阴影部分的底长为x,高,
∴,
∴.
即.
故选:D.
【点睛】此题考查解一元二次方程、平行四边形的判定及性质,平移的性质,等腰直角三角形的判定,根据平移的性质得到四边形是平行四边形是解题的关键.
8.B
【分析】设AP=xcm,则PB=(8 x)cm,求出∠A=45°,∠APR=90°,得到PR=PA=xcm,然后根据 PQCR的面积为△ABC面积的一半列方程求解即可.
【详解】解:设AP=xcm,则PB=(8 x)cm,
∵∠B=90°,AB=BC=8cm,
∴∠A=45°,
∵PRBC,
∴∠APR=90°,
∴PR=PA=xcm,
∵ PQCR的面积为△ABC面积的一半,
∴,
解得:,
∴点P移动的路程为4cm.
故选:B.
【点睛】本题主要考查了平行四边形的性质,一元二次方程的应用,根据几何图形的性质得出方程是解题的关键.
9.2或4/4或2
【分析】本题考查了一元二次方程的应用,理解题意,找出等量关系正确列方程是解题关键.设运动时间为,根据题意可得,,再根据三角形面积公式分两种情况求解即可.
【详解】解:设运动时间为,则,,
∵,,
∴cm,
∵线段将分成面积的两部分,
∴或,
∴,或,
整理得:或(无实数解),
解得,,
即线段将分成面积的两部分,运动时间为2或4秒.
故答案为:2或4.
10.3
【分析】本题主要考查动点问题,涉及解一元二次方程,根据题意得,,,,并求得t的取值范围为,利用面积公式可列出,求解即可.
【详解】解:∵点D从点C开始沿边运动,速度为,
∴,,
∵,点E从点B开始沿边运动,速度为,
∴,,
根据题意知t的最大值为,即,
∵,,
∴,
则,
解得: ,(舍去),
∴当时,.
故答案为:3.
11.或
【分析】本题考查了一元二次方程的应用,三角形面积,三角形中位线定理,过点作于,利用三角形中位线定理求得的长度;然后根据题意得,然后列出方程,求出方程的解即可,掌握知识点的应用是解题的关键.
【详解】根据题意得:,,
∴,,
过点作于,
∵,即,
∴,
又∵是的中点,
∴,是的中位线,
∴,
∵,
∴,
整理,得,
解得:,,即当或时,的面积是,
故答案为:或.
12.9或12
【分析】本题考查了一元二次方程的应用以及勾股定理,设运动t秒时,P,Q两点相距15厘米,利用勾股定理结合,可得出关于t的一元二次方程,解之即可得出结论
【详解】解:设运动t秒时,P,Q两点相距15厘米,
依题意,得:,
解得:,
∴运动9秒或12秒时,P,Q两点相距15厘米;
故答案为:9或12.
13.2或
【分析】本题主要考查一元二次方程的应用的知识点,解答本题的关键是Q点的运动位置,此题很容易漏掉一种情况,此题难度一般.设经过x秒,的面积等于,分类讨论当秒时,Q点在上运动,P在上运动,求出面积的表达式,求出一个值,当秒时,Q点在上运动,P在上运动,根据条件列出一个一元一次方程,求出一个值.
【详解】解:设经过x秒,的面积等于,
当秒时,Q点在上运动,P在上运动,
,,
∴,
解得或4,
又知,
故符合题意,
当秒时,Q点在上运动,P在上运动,
,
解得.
故答案为:2或.
14.1或4
【分析】本题考查了菱形的性质,一元二次方程的应用及分类讨论的数学思想,解题的关键是根据出发后时间的多少确定列方程的方法.
根据点、运动过程中与点的位置关系,分当时,点在线段上,点在线段上、当时,点在线段上,点在线段上和当时,点在线段上,点在线段上三种情况分别讨论.
【详解】解:设出发后秒时,.
四边形是菱形,,,
,,,,
,
当时,点在线段上,点在线段上.
此时,,
则;
解得,(舍去)
当时,点在线段上,点在线段上,
此时,
则;化简为,
此时方程,原方程无实数解;
当时,点在线段上,点在线段上,
此时,,
则;
解得(舍去),
综上所述,出发后或时,.
故答案为:1或4.
15.或或
【分析】过点作于点,则,当运动时间为秒时,,,,,根据的面积等于,即可得出关于t的一元二次方程,解之取其符合题意的值即可得出结论.
【详解】解:过点作于点,则,如图所示.
当运动时间为秒时, ,,, ,
依题意得:.
当时,,
解得:,;
当时,,
解得:不符合题意,舍去,.
经过或或秒后,的面积等于.
故答案为:或或.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
16.或
【分析】本题考查矩形的判定和性质,等腰三角形的判定和性质,勾股定理,解一元二次方程等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.本题应分三种情况进行讨论,①若,在中,由,,将各数据代入,可将时间求出;
②若,在中,由,,将数据代入,可将时间求出;
③若,则,可将时间求出.
【详解】解:过点作于,则四边形为矩形.
由图可知,,,若以、、为顶点的三角形是等腰三角形,可以分三种情况:
①若,在中,,由得,解得;
②若,在中,,由得,即,
此时,,
所以此方程无解,.
③若,则,,
综上所述,当或时,以,,三点为顶点的三角形是等腰三角形.
故答案为:或.
17.(1)3秒
(2)不能
【分析】此题主要考查了一元一次方程,一元二次方程的应用以及勾股定理的应用,三角形的面积,找到关键描述语得出等量关系是解决问题的关键.
(1)设出发t秒时,则,,根据的长度等于,在中,由勾股定理可得答案;
(2)令,根据三角形的面积公式列出方程,再根据得出方程没有实数根,从而得出的面积不能等于.
【详解】(1)解:设出发t秒时,则,,,
根据题意得,,
∴,
解得:(不符合题意,舍去),.
故3秒后,的长度为.
(2)解:不能,
假设经过t秒后,的面积等于,
即,
∴,
整理得:,
由于,
则方程没有实数根,
∴的面积不能等于.
18.(1),
(2)当的值为或时,的长为;
(3)当时,使得五边形的面积等于.
【分析】本题考查了一元二次方程的应用,以及勾股定理的应用,利用含t的代数式表示各自线段的关系,根据题干数量关系即可确立等量关系式是解题的关键.
(1)根据点从点开始沿边向终点以的速度移动,可以求得;
(2)用含的代数式分别表示和的值,运用勾股定理列式,据此求出值;
(3)根据题干信息使得五边形的面积等于的值存在,利用长方形的面积减去的面积即可,则的面积为,由此求得值.
【详解】(1)解:点从点开始沿边向终点以的速度移动,,故为,
点从点开始沿向终点以的速度移动,故,
故答案为:,;
(2)解:由题意得:,
解得:,;
当的值为或时,的长度等于;
(3)解:存在,能够使得五边形的面积等于.理由如下:
长方形的面积是:,
使得五边形的面积等于,则的面积为,
,
解得:(不合题意舍去),.
即当时,使得五边形的面积等于.
19.(1),;
(2)为或时,的面积等于.
【分析】()根据题意列出代数式即可;
()根据,然后解一元二次方程即可求解;
本题考查了一元二次方程的应用,列代数式,读懂题意,列出一元二次方程是解题的关键.
【详解】(1)解:依题意可知:,,
∴,,
故答案为:,;
(2)解:由()得:,,,,
∵的面积等于,
∴,
∴,
∴,
整理得:,
解得:,,
答:为或时,的面积等于.
20.(1)
(2)8
(3)或或
【分析】本题主要考查了菱形的性质,动点问题,一元二次方程的应用,
对于(1),先根据菱形的性质求出,可确定时,两个点的位置,即可得出答案;
对于(2),先分别求出,再根据面积公式求出答案;
对于(3),分,,,四种情况,分别表示,再根据面积等于列出方程,求出解即可.
【详解】(1)∵四边形时菱形,
∴.
根据题意可知,
当时,
点M在上,点N在上,
∴,.
故答案为:,;
(2)当时,,
∴,
∴;
(3)存在,理由如下:
当时,
根据题意得,
∴,
∴,
解得或(舍);
当时,
根据题意得,
∴,
∴,
无解;
当时,
根据题意得,
∴,
∴,
解得或(舍);
当时,
根据题意得,
∴,
∴,
解得或(舍).
所以或或.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
专题 08:一元二次方程的应用(动态几何问题)--2024-2025年人教版九年级上册数学期末专题提升训练
一、单选题
1.如图,在矩形中,,,动点,同时出发,点从点出发以的速度向点移动,一直到达点为止,点从点出发以的速度向点移动,则当点和点的距离是时,,两点出发了( )
A. B.s或 C.s或 D.s
2.如图,中,,,,点P从点B出发向终点C以每秒1个单位长度的速度移动,点Q从点C出发向终点A以每秒2个单位长度的速度移动,P,Q两点同时出发,其中一点先到达终点时P,Q两点同时停止移动.则当的面积等于8时,经过了( )
A.1秒 B.6秒 C.8秒 D.1秒或8秒
3.如图所示,在中,,,,点P以的速度从点A开始沿边向点B移动,点Q以的速度从点B开始沿边向点C移动,且点P,Q分别从点A,B同时出发.若有一点到达目的地,则另一点同时停止运动.要使P,Q两点之间的距离等于,则需要经过( )
A. B. C. D.或
4.如图所示,中,,,,点从点开始沿向点以的速度移动,点从点开始沿边向点以的速度移动.如果、分别从、同时出发,那么多少秒后,线段将分成面积的两部分( )
A.2 B.4 C.2或4 D.2或6
5.如图,在中,,,,动点P,Q分别从点A,B同时开始沿,运动(运动方向如图所示),点P的速度为,点Q的速度为,当点Q移动到点C时,两点同时停止运动,设运动的时间为,当的面积为时,则可列方程为( )
A. B. C. D.
6.如图,在矩形中,,,点从点出发沿以的速度向点移动,一直到达点为止;同时,点从点出发沿边以的速度向点移动. 设运动时间为,当时,( )
A. B.或4 C.或 D.
7.如图,将边长为的正方形沿其对角线剪开,再把沿着方向平移,得到,若两个三角形重叠部分的面积为,则它移动的距离等于( )
A. B. C.或 D.
8.如图,在等腰中,,,动点P从点A出发沿向点B移动,作,,当的面积为面积的一半时,点P移动的路程为( )
A. B. C. D.
二、填空题
9.如图,中,,,,点从点开始沿向点以的速度运动,点从点开始沿边向点以的速度移动.如果、分别从、同时出发,那么 秒后,线段将分成面积的两部分.
10.如图,在中,,,,点D从点C开始沿边运动,速度为,与此同时,点E从点B开始沿边运动,速度为,当点E到达点C时,点D同时停止运动,连接,设运动时间为,的面积为S.当时, s.
11.如图,在中,,,,是中点,动点从点出发沿边向点以的速度移动,同时动点从点出发沿边向点以的速度移动,当运动到点时两点同时停止运动,连接、,为 时的面积为.
12.如图,在中,,动点P从点C出发,沿方向运动,动点Q从点B出发,沿方向运动,如果点P,Q的运动速度均为.那么运动 秒时,它们相距?
13.如图,在边长为正方形中,点P从点A开始沿边向点B以的速度移动,点Q从点B开始沿和边向D点以的速度移动,如果点P、Q分别从A、B同时出发,其中一点到终点,另一点也随之停止.过了 秒钟后,的面积等于.
14.如图,菱形中,,交于,,,动点从出发沿方向以每秒匀速直线运动到,动点从出发沿方向以每秒匀速直线运动到,若,同时出发,问出发后 s时,的面积为菱形面积的?
15.如图,在中,,,点从点出发,沿射线方向以的速度移动,点从点出发,沿射线方向以的速度移动,如果、两点同时出发,问:经过 秒后的面积等于.
16.如图,在四边形中,,,,,.动点P从点D出发,沿射线的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t秒,当 时,以B,P,Q三点为顶点的三角形是等腰三角形.
三、解答题
17.如图,在中,,,,点从点开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动.若,两点同时出发,当点运动到点时,,两点同时停止运动.求:
(1)经过几秒后,的长度等于?
(2)请直接写出的面积能否等于?
18.在长方形中,,,点从点开始沿边向终点以的速度移动,与此同时,点从点开始沿向终点以的速度移动,如果,分别从,同时出发,当点运动到点时,两点停止运动.设运动时间为.
(1)填空:________,_______(用含的代数式表示);
(2)当为何值时,的长为?
(3)是否存在的值,使得五边形的面积等于?若存在,请求出此时的值,若不存在,请说明理由.
19.在矩形中,,,点从出发,沿以的速度向点B匀速移动,同时点从点出发,沿以的速度向点匀速移动.设运动的时间为.
(1)______,______;
(2)为何值时,的面积等于?
20.如图,菱形中, 交于点 O, ,动点 M 从 A 点出发沿方向以匀速直线运动到 C 点,动点 N 从 B 点出发沿方向以匀速直线运动到 D 点.若 M,N 同时出发,设运动时间为 t 秒:
(1)当时, , .(用 t 表示)
(2)当秒时, 的面积为多少?
(3)点 M 到达点 C 后立即原路返回,速度保持不变,直到点 N 到达 D 后同时停止运动,那么在整个移 动过程中,是否存在某一时刻,使得的面积为?若存在,求出运动时间;若不存在,请说 明理由.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
题号 1 2 3 4 5 6 7 8
答案 B A A C D C D B
1.B
【分析】本题考查了一元二次方程的应用,勾股定理,矩形的性质,利用勾股定理,找出等量关系是解题的关键.过点作于点,则四边形是矩形,当运动时间为秒时,,,则,根据题意得:,即,即可求解.
【详解】解:如图,过点作于点,则四边形是矩形,
(秒),
当运动时间为秒时,,,
,
根据题意得:,
即,
整理得:,
解得:,,
当点和点的距离是时,、两点出发了秒或秒.
故选:B.
2.A
【分析】本题考查了一元二次方程的应用,理解题意,找准等量关系,正确列出一元二次方程是解此题的关键.
设经过了秒,的面积等于8,用含的代数式表示和,根据三角形的面积公式建立方程,求解即可.
【详解】解:设经过了秒,的面积等于8,则
,
解得:,,
∵点Q从点C到点A需要的时间是:(秒),
∴,不合题意,应舍去,
因此,则当的面积等于8时,经过了1秒.
故答案为:A.
3.A
【分析】本题主要考查勾股定理以及一元二次方程的应用.根据勾股定理列出方程是解题的关键.
设经过,P、Q之间的距离等于,先用含x的代数式分别表示和的长度,进一步利用勾股定理建立方程求得答案即可.
【详解】设后P、Q之间的距离等于,
∵,
∴,
∵,
∴,
解得,(不合题意,舍去),
∴,
需要经过.
故选:A.
4.C
【分析】本题考查了一元二次方程的应用,理解题意,找出等量关系正确列方程是解题关键.
设运动时间为,根据题意可得,,再根据三角形面积公式分两种情况求解即可.
【详解】解:设运动时间为,则,
,
,
∵线段将分成面积的两部分,
或,
或,
整理得:或(无实数解).
解得:,
即线段将分成面积的两部分,运动时间为2或4秒.
故选:C.
5.D
【分析】本题考查一元二次方程在几何图形中的应用,当运动时,,,根据“的面积为”即可列出方程.
【详解】当运动时,,,,
∵,
∴,
即.
故选:D
6.C
【点评】此题考查了一元二次方程的运用.利用作垂线,构造直角三角形,运用勾股定理列方程是解题关键.
作,垂足为H,设运动时间为t秒,用t表示线段长,用勾股定理列方程求解.
【详解】解:设P,Q两点从出发经过t秒时,点P,Q间的距离是,
作,垂足为H,
则,,.
,
可得:,
解得,.
答:P,Q两点从出发经过或秒时,点P,Q间的距离是.
故答案为:C.
7.D
【分析】根据平移的性质,结合阴影部分是平行四边形,与都是等腰直角三角形,则若设,则阴影部分的底长为x,高,根据平行四边形的面积公式即可列出方程求解.
【详解】解:设交于H,交于点G,
由平移的性质知,,
∴四边形是平行四边形,
∵由正方形的性质可得:,,
∴是等腰直角三角形,
同理,也是等腰直角三角形,
设,则阴影部分的底长为x,高,
∴,
∴.
即.
故选:D.
【点睛】此题考查解一元二次方程、平行四边形的判定及性质,平移的性质,等腰直角三角形的判定,根据平移的性质得到四边形是平行四边形是解题的关键.
8.B
【分析】设AP=xcm,则PB=(8 x)cm,求出∠A=45°,∠APR=90°,得到PR=PA=xcm,然后根据 PQCR的面积为△ABC面积的一半列方程求解即可.
【详解】解:设AP=xcm,则PB=(8 x)cm,
∵∠B=90°,AB=BC=8cm,
∴∠A=45°,
∵PRBC,
∴∠APR=90°,
∴PR=PA=xcm,
∵ PQCR的面积为△ABC面积的一半,
∴,
解得:,
∴点P移动的路程为4cm.
故选:B.
【点睛】本题主要考查了平行四边形的性质,一元二次方程的应用,根据几何图形的性质得出方程是解题的关键.
9.2或4/4或2
【分析】本题考查了一元二次方程的应用,理解题意,找出等量关系正确列方程是解题关键.设运动时间为,根据题意可得,,再根据三角形面积公式分两种情况求解即可.
【详解】解:设运动时间为,则,,
∵,,
∴cm,
∵线段将分成面积的两部分,
∴或,
∴,或,
整理得:或(无实数解),
解得,,
即线段将分成面积的两部分,运动时间为2或4秒.
故答案为:2或4.
10.3
【分析】本题主要考查动点问题,涉及解一元二次方程,根据题意得,,,,并求得t的取值范围为,利用面积公式可列出,求解即可.
【详解】解:∵点D从点C开始沿边运动,速度为,
∴,,
∵,点E从点B开始沿边运动,速度为,
∴,,
根据题意知t的最大值为,即,
∵,,
∴,
则,
解得: ,(舍去),
∴当时,.
故答案为:3.
11.或
【分析】本题考查了一元二次方程的应用,三角形面积,三角形中位线定理,过点作于,利用三角形中位线定理求得的长度;然后根据题意得,然后列出方程,求出方程的解即可,掌握知识点的应用是解题的关键.
【详解】根据题意得:,,
∴,,
过点作于,
∵,即,
∴,
又∵是的中点,
∴,是的中位线,
∴,
∵,
∴,
整理,得,
解得:,,即当或时,的面积是,
故答案为:或.
12.9或12
【分析】本题考查了一元二次方程的应用以及勾股定理,设运动t秒时,P,Q两点相距15厘米,利用勾股定理结合,可得出关于t的一元二次方程,解之即可得出结论
【详解】解:设运动t秒时,P,Q两点相距15厘米,
依题意,得:,
解得:,
∴运动9秒或12秒时,P,Q两点相距15厘米;
故答案为:9或12.
13.2或
【分析】本题主要考查一元二次方程的应用的知识点,解答本题的关键是Q点的运动位置,此题很容易漏掉一种情况,此题难度一般.设经过x秒,的面积等于,分类讨论当秒时,Q点在上运动,P在上运动,求出面积的表达式,求出一个值,当秒时,Q点在上运动,P在上运动,根据条件列出一个一元一次方程,求出一个值.
【详解】解:设经过x秒,的面积等于,
当秒时,Q点在上运动,P在上运动,
,,
∴,
解得或4,
又知,
故符合题意,
当秒时,Q点在上运动,P在上运动,
,
解得.
故答案为:2或.
14.1或4
【分析】本题考查了菱形的性质,一元二次方程的应用及分类讨论的数学思想,解题的关键是根据出发后时间的多少确定列方程的方法.
根据点、运动过程中与点的位置关系,分当时,点在线段上,点在线段上、当时,点在线段上,点在线段上和当时,点在线段上,点在线段上三种情况分别讨论.
【详解】解:设出发后秒时,.
四边形是菱形,,,
,,,,
,
当时,点在线段上,点在线段上.
此时,,
则;
解得,(舍去)
当时,点在线段上,点在线段上,
此时,
则;化简为,
此时方程,原方程无实数解;
当时,点在线段上,点在线段上,
此时,,
则;
解得(舍去),
综上所述,出发后或时,.
故答案为:1或4.
15.或或
【分析】过点作于点,则,当运动时间为秒时,,,,,根据的面积等于,即可得出关于t的一元二次方程,解之取其符合题意的值即可得出结论.
【详解】解:过点作于点,则,如图所示.
当运动时间为秒时, ,,, ,
依题意得:.
当时,,
解得:,;
当时,,
解得:不符合题意,舍去,.
经过或或秒后,的面积等于.
故答案为:或或.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
16.或
【分析】本题考查矩形的判定和性质,等腰三角形的判定和性质,勾股定理,解一元二次方程等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.本题应分三种情况进行讨论,①若,在中,由,,将各数据代入,可将时间求出;
②若,在中,由,,将数据代入,可将时间求出;
③若,则,可将时间求出.
【详解】解:过点作于,则四边形为矩形.
由图可知,,,若以、、为顶点的三角形是等腰三角形,可以分三种情况:
①若,在中,,由得,解得;
②若,在中,,由得,即,
此时,,
所以此方程无解,.
③若,则,,
综上所述,当或时,以,,三点为顶点的三角形是等腰三角形.
故答案为:或.
17.(1)3秒
(2)不能
【分析】此题主要考查了一元一次方程,一元二次方程的应用以及勾股定理的应用,三角形的面积,找到关键描述语得出等量关系是解决问题的关键.
(1)设出发t秒时,则,,根据的长度等于,在中,由勾股定理可得答案;
(2)令,根据三角形的面积公式列出方程,再根据得出方程没有实数根,从而得出的面积不能等于.
【详解】(1)解:设出发t秒时,则,,,
根据题意得,,
∴,
解得:(不符合题意,舍去),.
故3秒后,的长度为.
(2)解:不能,
假设经过t秒后,的面积等于,
即,
∴,
整理得:,
由于,
则方程没有实数根,
∴的面积不能等于.
18.(1),
(2)当的值为或时,的长为;
(3)当时,使得五边形的面积等于.
【分析】本题考查了一元二次方程的应用,以及勾股定理的应用,利用含t的代数式表示各自线段的关系,根据题干数量关系即可确立等量关系式是解题的关键.
(1)根据点从点开始沿边向终点以的速度移动,可以求得;
(2)用含的代数式分别表示和的值,运用勾股定理列式,据此求出值;
(3)根据题干信息使得五边形的面积等于的值存在,利用长方形的面积减去的面积即可,则的面积为,由此求得值.
【详解】(1)解:点从点开始沿边向终点以的速度移动,,故为,
点从点开始沿向终点以的速度移动,故,
故答案为:,;
(2)解:由题意得:,
解得:,;
当的值为或时,的长度等于;
(3)解:存在,能够使得五边形的面积等于.理由如下:
长方形的面积是:,
使得五边形的面积等于,则的面积为,
,
解得:(不合题意舍去),.
即当时,使得五边形的面积等于.
19.(1),;
(2)为或时,的面积等于.
【分析】()根据题意列出代数式即可;
()根据,然后解一元二次方程即可求解;
本题考查了一元二次方程的应用,列代数式,读懂题意,列出一元二次方程是解题的关键.
【详解】(1)解:依题意可知:,,
∴,,
故答案为:,;
(2)解:由()得:,,,,
∵的面积等于,
∴,
∴,
∴,
整理得:,
解得:,,
答:为或时,的面积等于.
20.(1)
(2)8
(3)或或
【分析】本题主要考查了菱形的性质,动点问题,一元二次方程的应用,
对于(1),先根据菱形的性质求出,可确定时,两个点的位置,即可得出答案;
对于(2),先分别求出,再根据面积公式求出答案;
对于(3),分,,,四种情况,分别表示,再根据面积等于列出方程,求出解即可.
【详解】(1)∵四边形时菱形,
∴.
根据题意可知,
当时,
点M在上,点N在上,
∴,.
故答案为:,;
(2)当时,,
∴,
∴;
(3)存在,理由如下:
当时,
根据题意得,
∴,
∴,
解得或(舍);
当时,
根据题意得,
∴,
∴,
无解;
当时,
根据题意得,
∴,
∴,
解得或(舍);
当时,
根据题意得,
∴,
∴,
解得或(舍).
所以或或.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
