人教版七年级下册数学第五章第三节平行线的性质综合练习
文档属性
| 名称 | 人教版七年级下册数学第五章第三节平行线的性质综合练习 |  | |
| 格式 | zip | ||
| 文件大小 | 195.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-31 08:40:08 | ||
图片预览


文档简介
第五章第三节平行线的性质综合练习
一、选择题。
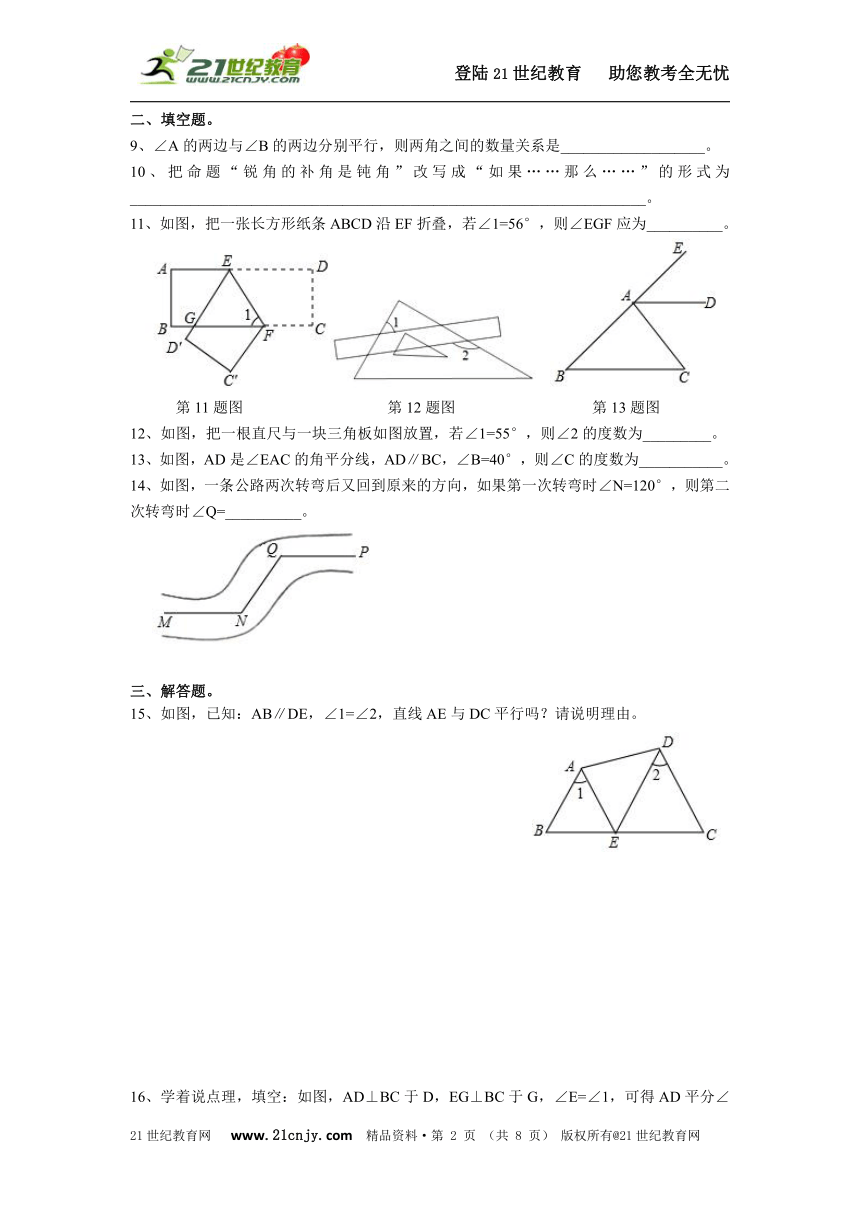
1、如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上。如果∠1=20°,那么∠2的度数是( )21·cn·jy·com
A.15° B.20° C.25° D.30°
第1题图 第2题图 第3题图
2、如图,在△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为( )www.21-cn-jy.com
A.60° B.65° C.70° D.75°
3、如图,四条直线a、b、c、d,其中a∥b,∠1=30°,∠2=75°,则∠3等于( )
A.30° B.40° C.45° D.75°
4、如图,∥,且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=35°,∠2的度数为( )。2·1·c·n·j·y
A.95° B.65° C.85° D.35°
第4题图 第5题图 第6题图
5、如图,将三角板的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
A.10° B.15° C.25° D.35°
6、如图,直线∥∥,等边△ABC的顶点B、C分别在直线、上,若边BC与直线的夹角∠1=25°,则边AB与直线的夹角∠2=( )【来源:21·世纪·教育·网】
A.25° B.30° C.35° D.45°
7、下列说法:①同位角相等;②两点之间,线段最短;③平行线间的距离相等;④在同一平面内,两条不平行的直线有且只有一个交点。其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8、在同一平面内,下列说法:①过两点有且只有一条直线;②两条不相同的直线有且只有一个公共点;③经过直线外一点有且只有一条直线与已知直线垂直;④经过直线外一点有且只有一条直线与已知直线平行。其中正确的有( )21·世纪*教育网
A.1个 B.2个 C.3个 D.4个
二、填空题。
9、∠A的两边与∠B的两边分别平行,则两角之间的数量关系是___________________。
10、把命题“锐角的补角是钝角”改写成“如果……那么……”的形式为____________________________________________________________________。
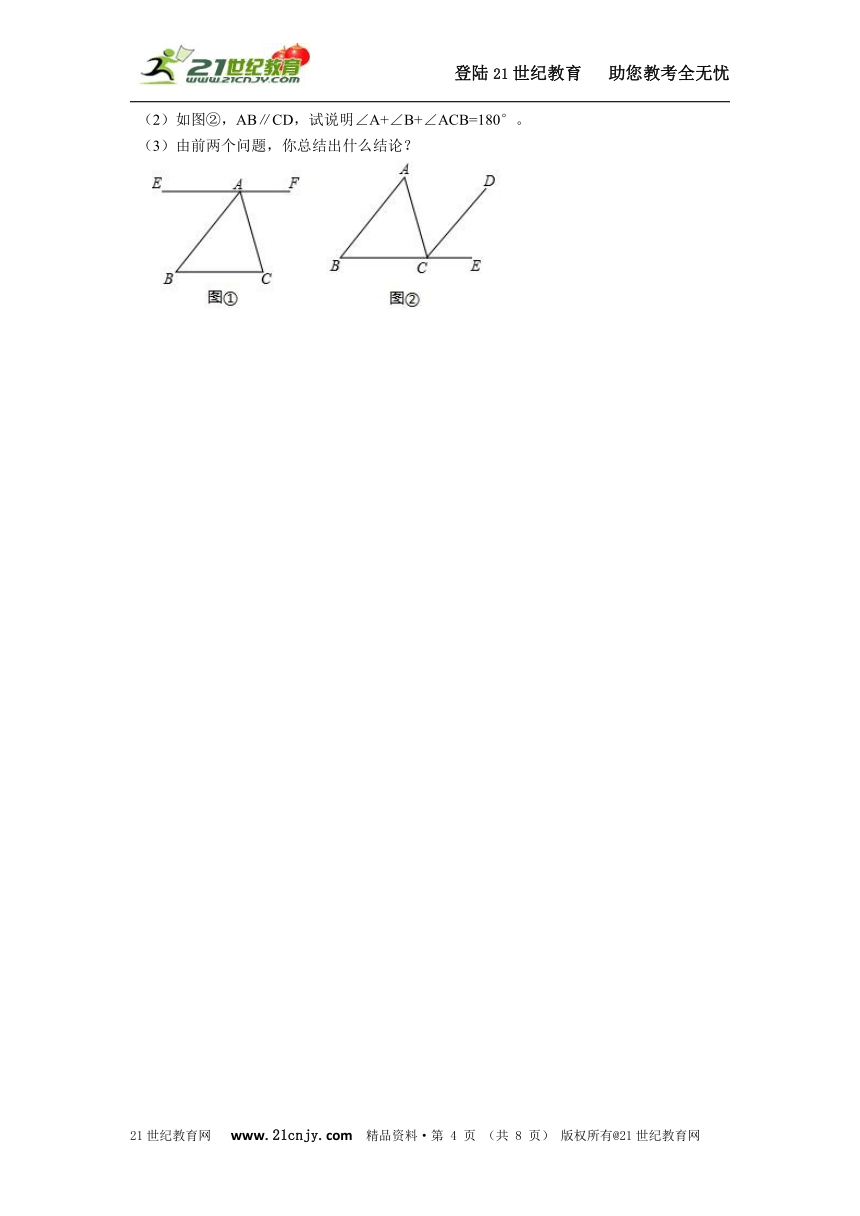
11、如图,把一张长方形纸条ABCD沿EF折叠,若∠1=56°,则∠EGF应为__________。
第11题图 第12题图 第13题图
12、如图,把一根直尺与一块三角板如图放置,若∠1=55°,则∠2的度数为_________。
13、如图,AD是∠EAC的角平分线,AD∥BC,∠B=40°,则∠C的度数为___________。
14、如图,一条公路两次转弯后又回到原来的方向,如果第一次转弯时∠N=120°,则第二次转弯时∠Q=__________。21教育网
三、解答题。
15、如图,已知:AB∥DE,∠1=∠2,直线AE与DC平行吗?请说明理由。
16、学着说点理,填空:如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,可得AD平分∠BAC。
理由如下:
∵AD⊥BC于D,EG⊥BC于G,(已知)
∴∠ADC=∠EGC=90°( )
∴AD∥EG,( )
∴∠1=∠2,( )
∠E=∠3(两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴_________=_________(等量代换)
∴AD平分∠BAC( )
17、如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=105°,∠ACF=25°,求∠FEC的度数。
18、(1)如图①,EF∥BC,试说明∠B+∠C+∠BAC=180°。
(2)如图②,AB∥CD,试说明∠A+∠B+∠ACB=180°。
(3)由前两个问题,你总结出什么结论?
参考答案与解析
答案:C
解析:【解答】
∵直尺的两边平行,∠1=20°
∴∠3=∠1=20°
∴∠2=45°-20°=25°
故选C。
【分析】本题考查了“两直线平行,内错角相等”的性质。
答案:D
解析:【解答】∵CD∥AB,∴∠CAB=∠ACD=65°
在△ABC中,∠ACB=180°-∠CAB-∠B=180°-65°-40°=75°,故选D。
【分析】本题考查平行线的性质(内错角相等)、三角形的内角和。
答案:C
解析:【解答】如图:
∵a∥b,∴∠2=∠1+∠4, ∴∠4=∠2-∠1=75°-30°=45°
∵∠3=∠4,∴∠3=45°。
【分析】本题考查平行线的性质、对顶角的性质。
答案:A
答案:C
解析:【解答】
如图,
∵直尺的两边互相平行,∠1=65°
∴∠3=65°(两直线平行,同位角相等)
∴∠2=90°-∠3=90°-65°=25°。故选C。
【分析】本题考查平行线的性质(两直线平行,同位角相等)
答案:C
解析:【解答】∵直线∥∥
∴∠3=∠1=25°
∵△ABC是等边三角形
∴∠4=60°-∠3=60°-25°=35°
∴∠2=∠4=35°。故选C。
【分析】本题考查平行线的性质、等边三角形的内角。
答案:C
解析:【解答】 两直线平行,同位角相等;若两直线不平行,同位角就不相等,故①错误;
两点之间,线段最短(上学期的知识),故②正确;
平行线间的距离(处处)相等,故③正确;
同一平面内,两条不平行的直线就是相交线,两条相交线有且只有一个交点是正确的,故④正确。所以正确的有3个,选C。 21世纪教育网版权所有
【分析】本题考查命题的真假性的判断,要熟悉从上学期开始学的定理。
答案:C
解析:【解答】过两点有且只有一条直线,也就是两点确定一条直线,故①正确;
两条不相同的直线可能没有交点(平行的情况),也可能有一个交点(相交的情况),故②错误;
③是垂直公理的一种情况,故③正确;
④是平行公理,故④正确。所以正确的说法有3个,故选C。
【分析】本题考查命题的真假性的判断,要熟悉从上学期开始学的定理。
10、答案:如果一个角是锐角的补角,那么这个角是钝角。
解析:【解答】“如果”后面是写命题的条件,“那么”后面是写命题的结论,结论是钝角,那么锐角的补角就必须作为条件(题设)。21cnjy.com
【分析】本题考查命题的改写,要正确区分题设与结论。
11、答案:68°。
解析:【解答】∵长方形的对边AD∥BC
∴∠1=∠1=56°
由翻折的性质和平角的定义可得∠3=180°-2∠2=180°-2×56°=68°
∵AD∥BC,∴∠EGF=∠3=68°。
【分析】本题考查平行线的性质、翻折的性质。
12、答案:145°。
解析:【解答】如图
∵∠1=55°,∴∠3=90°-∠1=90°-55°=35°
∴∠4=180°-∠3=145°
∵直尺的两边互相平行
∴∠2=∠4=145°。
【分析】本题考查了平行线的性质、直角三角形两锐角互余的性质、邻补角定义。
13、答案:40°
解析:【解答】∵AD∥BC,∴∠EAD=∠B,∠DAC=∠C
∵AD是∠EAC的平分线
∴∠EAD=∠DAC
∴∠B=∠C
∵∠B=40°
∴∠C=40°。
【分析】本题考查平行线的性质和角平分线的应用。
14、答案:120°
解析:【解答】依题意得,QP∥MN。
∴∠Q=∠N=120°
【分析】本题考查平行线的性质(两直线平行,内错角相等)
15、答案:AE∥DC。
解析:【解答】
解:AE∥DC,理由如下:如图
∵AB∥DE(已知) ∴∠1=∠3(两直线平行,内错角相等)
∵∠1=∠2(已知)
∴∠2=∠3(等量代换)
∴AE∥DC(内错角相等,两直线平行)
【分析】本题考查了平行线的性质、判定。
16、答案:垂直的定义;同位角相等,两直线平行;两直线平行,内错角相等;∠2=∠3;
角平分线的定义
解析:【解答】
∵AD⊥BC于D,EG⊥BC于G,(已知)
∴∠ADC=∠EGC=90°(垂直的定义)
∴AD∥EG,(同位角相等,两直线平行)
∴∠1=∠2,(两直线平行,内错角相等)
∠E=∠3(两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴∠2=∠3(等量代换)
∴AD平分∠BAC(角平分线的定义)
【分析】本题考查平行线的判定和性质的综合运用。
17、答案:25°。
解析:【解答】解:∵EF∥AD,AD∥BC,
∴EF∥AD∥BC
∴∠DAC+∠ACB=180°
∵∠DAC=105°,∠ACF=25°
又∵∠ACB+∠ACD+∠DCE=180°(平角的定义),∴∠A+∠B+∠ACB=180°(等量代换)
(3)从以上的两个问题中得出这样的结论:三角形的内角和是180°。
【分析】利用平行线的性质来证明与探究,得出“三角形的内角和是180°”的结论。
一、选择题。
1、如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上。如果∠1=20°,那么∠2的度数是( )21·cn·jy·com
A.15° B.20° C.25° D.30°
第1题图 第2题图 第3题图
2、如图,在△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为( )www.21-cn-jy.com
A.60° B.65° C.70° D.75°
3、如图,四条直线a、b、c、d,其中a∥b,∠1=30°,∠2=75°,则∠3等于( )
A.30° B.40° C.45° D.75°
4、如图,∥,且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=35°,∠2的度数为( )。2·1·c·n·j·y
A.95° B.65° C.85° D.35°
第4题图 第5题图 第6题图
5、如图,将三角板的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
A.10° B.15° C.25° D.35°
6、如图,直线∥∥,等边△ABC的顶点B、C分别在直线、上,若边BC与直线的夹角∠1=25°,则边AB与直线的夹角∠2=( )【来源:21·世纪·教育·网】
A.25° B.30° C.35° D.45°
7、下列说法:①同位角相等;②两点之间,线段最短;③平行线间的距离相等;④在同一平面内,两条不平行的直线有且只有一个交点。其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8、在同一平面内,下列说法:①过两点有且只有一条直线;②两条不相同的直线有且只有一个公共点;③经过直线外一点有且只有一条直线与已知直线垂直;④经过直线外一点有且只有一条直线与已知直线平行。其中正确的有( )21·世纪*教育网
A.1个 B.2个 C.3个 D.4个
二、填空题。
9、∠A的两边与∠B的两边分别平行,则两角之间的数量关系是___________________。
10、把命题“锐角的补角是钝角”改写成“如果……那么……”的形式为____________________________________________________________________。
11、如图,把一张长方形纸条ABCD沿EF折叠,若∠1=56°,则∠EGF应为__________。
第11题图 第12题图 第13题图
12、如图,把一根直尺与一块三角板如图放置,若∠1=55°,则∠2的度数为_________。
13、如图,AD是∠EAC的角平分线,AD∥BC,∠B=40°,则∠C的度数为___________。
14、如图,一条公路两次转弯后又回到原来的方向,如果第一次转弯时∠N=120°,则第二次转弯时∠Q=__________。21教育网
三、解答题。
15、如图,已知:AB∥DE,∠1=∠2,直线AE与DC平行吗?请说明理由。
16、学着说点理,填空:如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,可得AD平分∠BAC。
理由如下:
∵AD⊥BC于D,EG⊥BC于G,(已知)
∴∠ADC=∠EGC=90°( )
∴AD∥EG,( )
∴∠1=∠2,( )
∠E=∠3(两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴_________=_________(等量代换)
∴AD平分∠BAC( )
17、如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=105°,∠ACF=25°,求∠FEC的度数。
18、(1)如图①,EF∥BC,试说明∠B+∠C+∠BAC=180°。
(2)如图②,AB∥CD,试说明∠A+∠B+∠ACB=180°。
(3)由前两个问题,你总结出什么结论?
参考答案与解析
答案:C
解析:【解答】
∵直尺的两边平行,∠1=20°
∴∠3=∠1=20°
∴∠2=45°-20°=25°
故选C。
【分析】本题考查了“两直线平行,内错角相等”的性质。
答案:D
解析:【解答】∵CD∥AB,∴∠CAB=∠ACD=65°
在△ABC中,∠ACB=180°-∠CAB-∠B=180°-65°-40°=75°,故选D。
【分析】本题考查平行线的性质(内错角相等)、三角形的内角和。
答案:C
解析:【解答】如图:
∵a∥b,∴∠2=∠1+∠4, ∴∠4=∠2-∠1=75°-30°=45°
∵∠3=∠4,∴∠3=45°。
【分析】本题考查平行线的性质、对顶角的性质。
答案:A
答案:C
解析:【解答】
如图,
∵直尺的两边互相平行,∠1=65°
∴∠3=65°(两直线平行,同位角相等)
∴∠2=90°-∠3=90°-65°=25°。故选C。
【分析】本题考查平行线的性质(两直线平行,同位角相等)
答案:C
解析:【解答】∵直线∥∥
∴∠3=∠1=25°
∵△ABC是等边三角形
∴∠4=60°-∠3=60°-25°=35°
∴∠2=∠4=35°。故选C。
【分析】本题考查平行线的性质、等边三角形的内角。
答案:C
解析:【解答】 两直线平行,同位角相等;若两直线不平行,同位角就不相等,故①错误;
两点之间,线段最短(上学期的知识),故②正确;
平行线间的距离(处处)相等,故③正确;
同一平面内,两条不平行的直线就是相交线,两条相交线有且只有一个交点是正确的,故④正确。所以正确的有3个,选C。 21世纪教育网版权所有
【分析】本题考查命题的真假性的判断,要熟悉从上学期开始学的定理。
答案:C
解析:【解答】过两点有且只有一条直线,也就是两点确定一条直线,故①正确;
两条不相同的直线可能没有交点(平行的情况),也可能有一个交点(相交的情况),故②错误;
③是垂直公理的一种情况,故③正确;
④是平行公理,故④正确。所以正确的说法有3个,故选C。
【分析】本题考查命题的真假性的判断,要熟悉从上学期开始学的定理。
10、答案:如果一个角是锐角的补角,那么这个角是钝角。
解析:【解答】“如果”后面是写命题的条件,“那么”后面是写命题的结论,结论是钝角,那么锐角的补角就必须作为条件(题设)。21cnjy.com
【分析】本题考查命题的改写,要正确区分题设与结论。
11、答案:68°。
解析:【解答】∵长方形的对边AD∥BC
∴∠1=∠1=56°
由翻折的性质和平角的定义可得∠3=180°-2∠2=180°-2×56°=68°
∵AD∥BC,∴∠EGF=∠3=68°。
【分析】本题考查平行线的性质、翻折的性质。
12、答案:145°。
解析:【解答】如图
∵∠1=55°,∴∠3=90°-∠1=90°-55°=35°
∴∠4=180°-∠3=145°
∵直尺的两边互相平行
∴∠2=∠4=145°。
【分析】本题考查了平行线的性质、直角三角形两锐角互余的性质、邻补角定义。
13、答案:40°
解析:【解答】∵AD∥BC,∴∠EAD=∠B,∠DAC=∠C
∵AD是∠EAC的平分线
∴∠EAD=∠DAC
∴∠B=∠C
∵∠B=40°
∴∠C=40°。
【分析】本题考查平行线的性质和角平分线的应用。
14、答案:120°
解析:【解答】依题意得,QP∥MN。
∴∠Q=∠N=120°
【分析】本题考查平行线的性质(两直线平行,内错角相等)
15、答案:AE∥DC。
解析:【解答】
解:AE∥DC,理由如下:如图
∵AB∥DE(已知) ∴∠1=∠3(两直线平行,内错角相等)
∵∠1=∠2(已知)
∴∠2=∠3(等量代换)
∴AE∥DC(内错角相等,两直线平行)
【分析】本题考查了平行线的性质、判定。
16、答案:垂直的定义;同位角相等,两直线平行;两直线平行,内错角相等;∠2=∠3;
角平分线的定义
解析:【解答】
∵AD⊥BC于D,EG⊥BC于G,(已知)
∴∠ADC=∠EGC=90°(垂直的定义)
∴AD∥EG,(同位角相等,两直线平行)
∴∠1=∠2,(两直线平行,内错角相等)
∠E=∠3(两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴∠2=∠3(等量代换)
∴AD平分∠BAC(角平分线的定义)
【分析】本题考查平行线的判定和性质的综合运用。
17、答案:25°。
解析:【解答】解:∵EF∥AD,AD∥BC,
∴EF∥AD∥BC
∴∠DAC+∠ACB=180°
∵∠DAC=105°,∠ACF=25°
又∵∠ACB+∠ACD+∠DCE=180°(平角的定义),∴∠A+∠B+∠ACB=180°(等量代换)
(3)从以上的两个问题中得出这样的结论:三角形的内角和是180°。
【分析】利用平行线的性质来证明与探究,得出“三角形的内角和是180°”的结论。
