2024-2025年人教版九年级上册数学期末专题提升训练22:二次函数的最值(含解析)
文档属性
| 名称 | 2024-2025年人教版九年级上册数学期末专题提升训练22:二次函数的最值(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 08:35:11 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
专题22:二次函数的最值--2024-2025年人教版九年级上册数学期末专题提升
一、单选题
1.从地面竖直向上抛出一小球,根据物理学规律,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是,则小球运动中的最大高度是( )
A. B. C. D.
2.若函数;当时,此时该函数的最小值是( )
A. B. C. D.
3.已知二次函数(a,b是实数),设该函数最小值为k,下列说法正确的是( )
A.若,则
B.若,则
C.若,则
D.若,则
4.二次函数在时有最小值3,则这个函数的图象可以是( )
A.B.
C.D.
5.已知,则的最大值为( )
A. B.4 C.0 D.
6.数学课上,老师给出以下探究问题:“已知二次函数,当时,函数最大值为8,求最小值.”下列关于此题求解所需条件的说法,正确的是()
A.只需知道,便可求 B.只需知道,便可求
C.,需都知道,才能求t D.即使,都知道,仍无法求
7.已知二次函数,当时,函数取得最大值;当时,函数取得最小值,则t的取值范围是( )
A. B. C. D.
8.已知二次函数(a,b,c为常数,)的图象如图所示,有下列四个结论,其中正确的是( )
①一元二次方程的根为;
②若点在该抛物线上,则;
③对于任意实数m,都有;
④若(p为常数,)的根为整数,则p的值只有两个
A.①② B.①③ C.③④ D.①③④
二、填空题
9.飞机着陆后滑行的距离(单位:)关于滑行的时间(单位:)的函数解析式是,飞机着陆后滑行 米才能停下来.
10.已知抛物线,当时,函数的最大值是6,最小值是2,则的取值范围是 .
11.点在二次函数的图象上,则的最小值是 .
12.如图,P是抛物线在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形周长的最大值为 .
13.已知:二次函数在的范围内有最小值,则这个最小值是 .
14.飞机着陆后滑行的距离s(单位:m)关于滑行的时间(单位:)的函数解析式是.则飞机着陆后滑行 才能停下来.
15.对于二次函数,点和在函数图象上,则 (填“>”,“=”或“<”);当时,函数的最小值为1,则的值为 .
16.如图,已知抛物线与x轴交于A,B两点,与y轴交于点C,点B的坐标为.点P是抛物线对称轴上的一个动点,当的周长最小时,则点P的坐标为 .
三、解答题
17.已知抛物线的顶点坐标为,且经过点.
(1)求抛物线对应的函数表达式;
(2)当时,求函数的最大值.
18.某数学兴趣小组在暑假开展社会实践活动,销售某品牌书包,平均每天可以销售20个,每个盈利12元,为了扩大销售,增加盈利,该小组决定采取适当的降价措施,经调查发现,如果每个书包每降价1元,平均每天可以多卖5个.
(1)若该兴趣小组同学想要一天盈利300元,每个书包应降价多少元;
(2)该兴趣小组同学想要一天盈利最大,应降价多少元,所得最大利润是多少元?
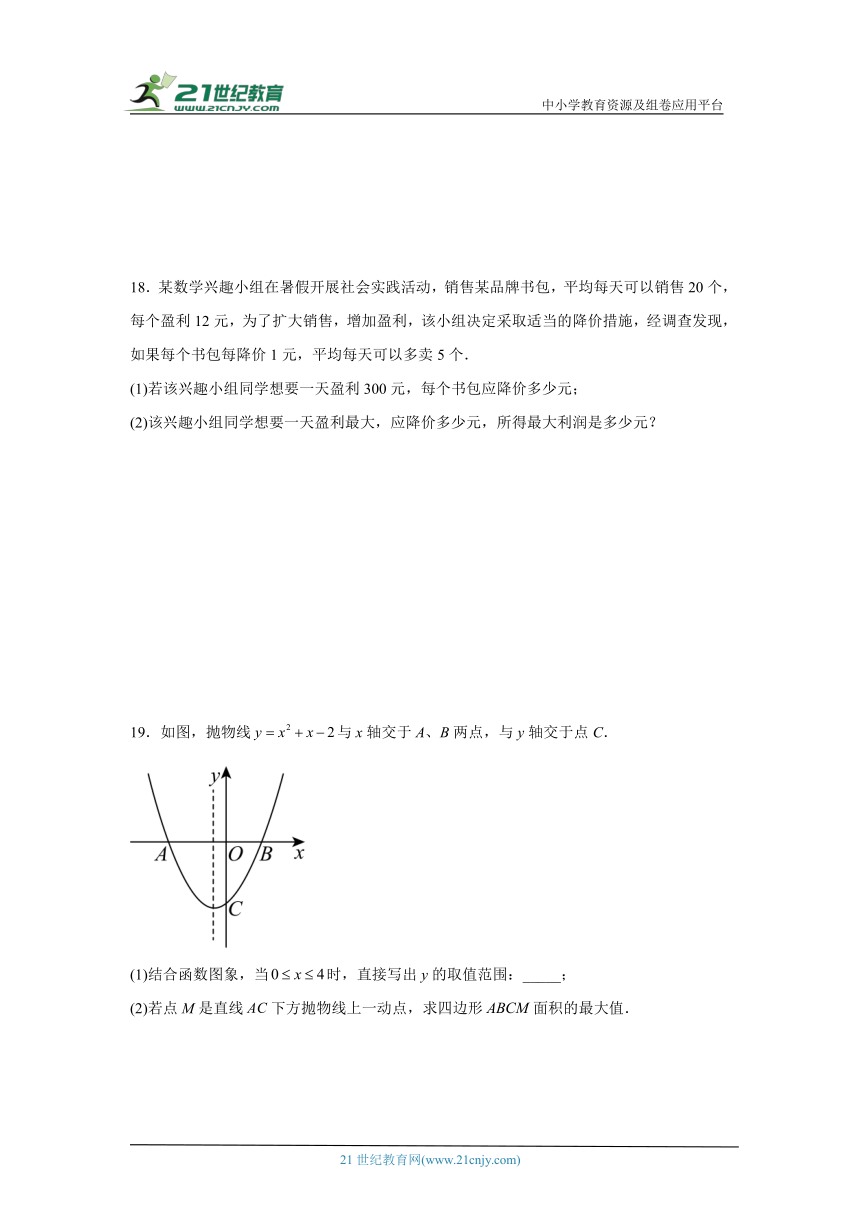
19.如图,抛物线与x轴交于A、B两点,与y轴交于点C.
(1)结合函数图象,当时,直接写出y的取值范围:_____;
(2)若点M是直线下方抛物线上一动点,求四边形面积的最大值.
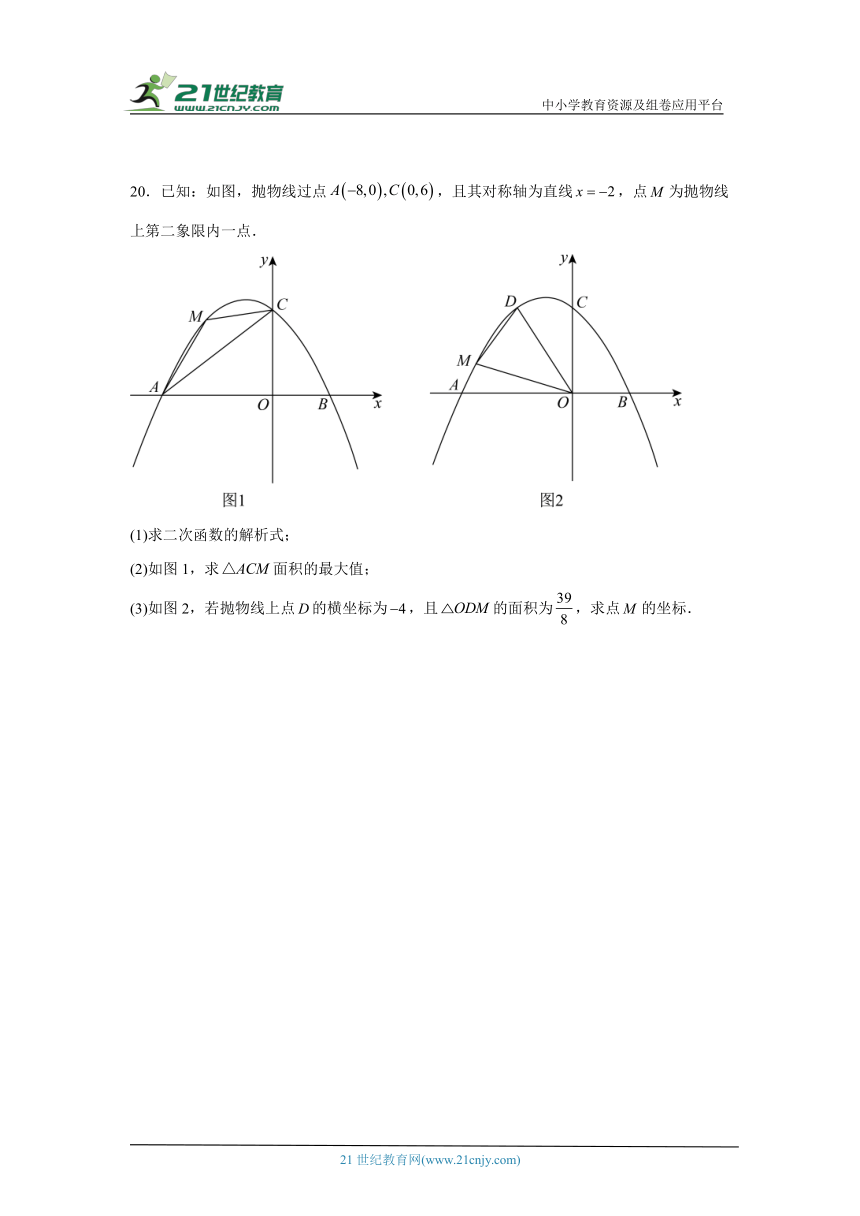
20.已知:如图,抛物线过点,且其对称轴为直线,点为抛物线上第二象限内一点.
(1)求二次函数的解析式;
(2)如图1,求面积的最大值;
(3)如图2,若抛物线上点的横坐标为,且的面积为,求点的坐标.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
题号 1 2 3 4 5 6 7 8
答案 C A B B B A C B
1.C
【分析】本题主要考查了二次函数的应用.先将二次函数一般式化为顶点式,再根据二次函数性质即可求解.
【详解】解:,
∵,,
∴当时,有最大值,最大值为45,
∴小球运动中的最大高度是.
故选:C.
2.A
【分析】本题主要考查了二次函数的的性质等知识点,根据函数的取值范围确定函数最小值出现在哪个函数上,然后再根据二次函数的性质即可得解,熟练掌握二次函数的性质是解决此题的关键.
【详解】解:∵函数,
∴当时,函数的最小值在函数上,
∴当时,该函数的最小值是3,
故选:A.
3.B
【分析】本题考查了二次函数的性质,二次函数的最值.利用抛物线解析式求得对称轴,即可求得函数的最小值,然后根据、的取值,判断的值,从而判断的大小.
【详解】解:解:由二次函数可知对称轴为直线,
函数的最小值,
若,,则,
,
若,,则,
,
故选项B正确,选项A、C、D错误.
故选:B.
4.B
【分析】本题考查了二次函数的最值问题,抛物线开口向上,在顶点处取得最小值,开口向下,二次函数在顶点处取得最大值.根据二次函数最值问题对各选项分析判断即可得解.
【详解】解:A、函数值3不是最小值,故本选项错误;
B、时有最小值3,故本选项正确;
C、时有最大值3,故本选项错误;
D、函数有最大值3,故本选项错误.
故选:B.
5.B
【分析】本题考查了二次函数的最值问题,整理出的表达式,考虑利用二次函数求解是解题的关键.
整理得到的表达式,再根据二次函数的最值问题和平方数非负数的性质解答.
【详解】解:∵,
,
,
,
当时,或,
∴当时,,
,
,
,
∴当时,有最大值4.
故选:B.
6.A
【分析】本题考查了二次函数的图象与系数的关系,二次函数的最值问题,在本题中分类讨论思想运用是解题的关键.先根据二次函数的已知条件,得出二次函数的图象开口向上,再分别进行讨论,即可得出函数的最大值与最小值即可得到结论.
【详解】解:二次函数,
该抛物线的对称轴为直线,且,
当,
当时,二次函数有最大值为:,即,
当时,二次函数有最小值为:,即,
当,
当时,二次函数有最大值为:,
当时,二次函数有最小值为:,即,
当,
此时当时,函数有最大值,
当时,函数有最小值,即,
,当时,函数有最大值,当时,函数有最小值,即,
,当或1时.函数有最大值,
当时,函数有最小值,即,
的值与有关,但与无关,
故选:.
7.C
【分析】本题考查了二次函数的图象与性质,二次函数的最值等知识.熟练掌握二次函数的图象与性质是解题的关键.
由,可知图象开口向上,对称轴为直线,顶点坐标为,当时,,即关于对称轴对称的点坐标为,由当时,函数取得最大值;当时,函数取得最小值,可得,计算求解,然后作答即可.
【详解】解:∵,
∴图象开口向上,对称轴为直线,顶点坐标为,
当时,,
∴关于对称轴对称的点坐标为,
∵当时,函数取得最大值;当时,函数取得最小值,
∴,
解得,,
故选:C.
8.B
【分析】本题主要考查了二次函数与一元二次方程之间的关系,二次函数与一次函数之间的关系,二次函数的性质等等,抛物线与x轴的交点的横坐标即为对应的一元二次方程的解,据此可判断①;根据增减性即可判断②;根据对称轴处函数有最大值即可判断③;直线与抛物线的交点的横坐标即为方程的根,求出根的情况即可判断④.
【详解】解:由函数图象可知,抛物线与x轴的两个交点坐标为,
∴一元二次方程的根为,故①正确;
∵抛物线开口向下,
∴离对称轴越远函数值越小,
∵抛物线对称轴为直线,且,
∴,故②错误;
当时,y有最大值,最大值为,
∴,即,故③正确;
根据题意可得直线与抛物线的交点的横坐标即为方程的根,
∵,
∴方程的根可以为或或,
∴对应的P的值有三个,故④错误;
故选:B.
9.
【分析】本题主要考查二次函数的应用,根据题意得出飞机滑行的距离即为s的最大值,将函数解析式配方成顶点式求出s的最大值即可得.
【详解】解:∵,
∴当时,取得最大值,即飞机着陆后滑行米才能停下来,
故答案为:.
10.
【分析】本题考查了二次函数的最值问题,先将解析式配方成顶点式,根据二次函数的增减性和最值问题解答.
【详解】解:,抛物线顶点坐标,开口向上,对称轴为直线,
∵时,函数y的最大值是6,最小值是2,
当函数值为2时,,
解得,
当函数值为6时,,
解得:或.
∴.
故答案为:.
11.1
【分析】本题考查了二次函数图象上点的坐标特征,二次函数的最值.代入点,得到,化简并配方,根据二次函数性质解答即可.
【详解】解:把代入二次函数中得,
,
∴
,
∵,
∴当时,有最小值,最小值为1.
故答案为:1.
12.8
【分析】本题考查了二次函数的最值及二次函数的图像上点的坐标特征,最后根据二次函数的性质求最值是解题的关键.
设点P的坐标为,,根据四边形的周长得到:,再由二次函数的性质即可求得最大值.
【详解】解:当,则,
解得:,
设点P的坐标为,,
由题意可知:四边形的周长,
∴,
∵,
当时,C有最大值8.
故答案为:8.
13.
【分析】此题考查了二次函数的性质,二次函数的最值,正确理解二次函数的性质是解题的关键.判断图象开口向下,顶点坐标为,结合,,可得当时,函数取最小值,再进一步可得答案.
【详解】解:∵,
∴图象开口向下,顶点坐标为,
∵,,
∵当时,函数有最小值,
∴当时,函数取最小值,最小值为:;
故答案为:.
14.
【分析】本题考查了二次函数的应用,把二次函数解析式转化为顶点式,求出二次函数的最大值即可求解,掌握配方法是解题的关键.
【详解】解:∵,
∴当时,有最大值为,
∴飞机着陆后滑行才能停下来,
故答案为:.
15. > 0或3.
【分析】本题考查了二次函数的图象性质,把点和代入进行计算,即可判断和;结合在时,随的增大而减小;在时,随的增大而增大,所以分类讨论:当时,则把代入,当时,把代入,进行计算即可作答.
【详解】解:∵二次函数,点和在函数图象上,
∴,,
∴;
∵函数,
∴二次函数的顶点坐标为,开口向上,
则在时,随的增大而减小;在时,随的增大而增大;
当时,函数的最小值为1,
∴当时,则把代入,
得,
解得(舍去),
∴当时,把代入,
得,
解得(舍去),
综上:的值为0或3.
故答案为:>,0或3.
16.
【分析】本题考查了用待定系数法求二次函数的解析式、轴对称的性质、一次函数;其中熟练运用轴对称的性质转化线段是解题的关键.根据抛物线的对称性可知:,所以当点在线段上时,的值最小,的周长也最小,以此为依据求解即可;
【详解】解:令,则,
解得,,
,,
抛物线的对称轴为:
点的横坐标为:
当 时, ;
设直线解析式为,
则,
解得,
由抛物线的对称性可知:
∴当点在线段上时,有最小值,则的周长最小,
将 代入得:
故此时点的坐标是
故答案为:.
17.(1)抛物线对应的函数表达式为
(2)在中,当时,有最大值为
【分析】本题考查二次函数综合,涉及待定系数法确定函数表达式、二次函数图象与性质求最值等知识,熟练掌握待定系数法确定函数表达式、二次函数图象与性质求最值的方法是解决问题的关键.
(1)根据题意,设出二次函数顶点式,利用待定系数法确定函数表达式即可得到答案;
(2)由(1)中所求表达式,利用二次函数图象与性质即可求出当时,函数的最大值.
【详解】(1)解:抛物线的顶点坐标为,
设函数表达式为,
把代入得:,
解得:,
抛物线对应的函数表达式为;
(2)解:由(1)知抛物线对应的函数表达式为,
抛物线开口向上、对称轴为,
当时,随的增大而增大,
在中,当时,有最大值为.
18.(1)元或元
(2)元,元
【分析】(1)设每个书包应降价元,则每个书包盈利元,平均每天可售出个,根据“数学兴趣小组每天销售该品牌书包获得的总利润每个书包的销售利润每天的销售量”,即可得出关于的一元二次方程,解之即可得出的值,进而得出结论;
(2)设每个书包降价元,则每个书包盈利元,平均每天可售出个,设每天盈利为元,根据“数学兴趣小组每天销售该品牌书包获得的总利润每个书包的销售利润每天的销售量”,即可得出关于的二次函数,求该二次函数的最值,即可得出结论.
【详解】(1)解:设每个书包应降价元,则每个书包盈利元,平均每天可售出个,
依题意可得:,
整理,得:,
解得:,,
每个书包应降价元或元;
(2)解:设每个书包降价元,则每个书包盈利元,平均每天可售出个,设每天盈利为元,
依题意可得:,
整理,得:,
,
抛物线开口向下,
当时,取得最大值,最大值为,
答:该兴趣小组同学想要一天盈利最大,应降价元,所得最大利润是元.
【点睛】本题主要考查了一元二次方程的应用(营销问题),因式分解法解一元二次方程,实际问题与二次函数(销售问题),把化成顶点式,二次函数的图象与系数的关系,二次函数的最值等知识点,根据“数学兴趣小组每天销售该品牌书包获得的总利润每个书包的销售利润每天的销售量”正确列出一元二次方程或二次函数解析式是解题的关键.
19.(1)
(2)四边形面积的最大值为4.
【分析】(1)根据抛物线解析式求得当和时y的值,再结合函数图象作答即可;
(2)过点M作轴于点N,连接,设点,则,,根据构建二次函数,利用二次函数的性质求出最大值即可解决问题.
【详解】(1)解:对于,
令,则,即,
令,则,
由函数图象知,当时,y的取值范围为,
故答案为:.
(2)如图,过点M作轴于点N,连接,
令,则,
解得:,
,
设,则,,
,
,
,
,
当时,有最大值为4,
四边形面积的最大值为4.
【点睛】本题考查了抛物线与x轴的交点、二次函数的图象与性质、二次函数的面积问题、二次函数的最值问题,解题的关键是灵活运用所学知识解决问题,学会构建二次函数解决最值问题.
20.(1)
(2)12
(3)点的坐标为
【分析】本题考查待定系数法求函数解析式、二次函数的图象与性质、坐标与图形,正确求得函数表达式是解答的关键.
(1)先求得抛物线与x轴的另一个交点坐标,然后利用待定系数法求解即可;
(2)先求得直线的解析式为,过点做轴的垂线分别交抛物线于点,交轴于点.设点,则点,由,结二次函数的性质求解即可;
(3)先求得点D坐标,连接,则轴.过点做交轴于点.根据等底等高的三角形面积相等得到,进而求得点N坐标和直线的解析式为.联立方程组求解即可.
【详解】(1)解:抛物线过点,且其对称轴为直线
抛物线过点
设二次函数的解析式为,
把代入,得:.
二次函数的解析式为;
(2)解:设的解析式为,把点代入,得.
的解析式为.
如图,过点做轴的垂线分别交抛物线于点,交轴于点.
设点,
则点
,
∵,
面积的最大值为12.
(3)解:点的横坐标为,
,直线的解析式为.
连接,则轴.过点做交轴于点.则
.
,
,则点的坐标为,
,直线的解析式为,
直线的解析式为.
点为抛物线与直线的在第二象限内的交点,
解方程组,解得或(舍去)
点的坐标为.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
专题22:二次函数的最值--2024-2025年人教版九年级上册数学期末专题提升
一、单选题
1.从地面竖直向上抛出一小球,根据物理学规律,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是,则小球运动中的最大高度是( )
A. B. C. D.
2.若函数;当时,此时该函数的最小值是( )
A. B. C. D.
3.已知二次函数(a,b是实数),设该函数最小值为k,下列说法正确的是( )
A.若,则
B.若,则
C.若,则
D.若,则
4.二次函数在时有最小值3,则这个函数的图象可以是( )
A.B.
C.D.
5.已知,则的最大值为( )
A. B.4 C.0 D.
6.数学课上,老师给出以下探究问题:“已知二次函数,当时,函数最大值为8,求最小值.”下列关于此题求解所需条件的说法,正确的是()
A.只需知道,便可求 B.只需知道,便可求
C.,需都知道,才能求t D.即使,都知道,仍无法求
7.已知二次函数,当时,函数取得最大值;当时,函数取得最小值,则t的取值范围是( )
A. B. C. D.
8.已知二次函数(a,b,c为常数,)的图象如图所示,有下列四个结论,其中正确的是( )
①一元二次方程的根为;
②若点在该抛物线上,则;
③对于任意实数m,都有;
④若(p为常数,)的根为整数,则p的值只有两个
A.①② B.①③ C.③④ D.①③④
二、填空题
9.飞机着陆后滑行的距离(单位:)关于滑行的时间(单位:)的函数解析式是,飞机着陆后滑行 米才能停下来.
10.已知抛物线,当时,函数的最大值是6,最小值是2,则的取值范围是 .
11.点在二次函数的图象上,则的最小值是 .
12.如图,P是抛物线在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形周长的最大值为 .
13.已知:二次函数在的范围内有最小值,则这个最小值是 .
14.飞机着陆后滑行的距离s(单位:m)关于滑行的时间(单位:)的函数解析式是.则飞机着陆后滑行 才能停下来.
15.对于二次函数,点和在函数图象上,则 (填“>”,“=”或“<”);当时,函数的最小值为1,则的值为 .
16.如图,已知抛物线与x轴交于A,B两点,与y轴交于点C,点B的坐标为.点P是抛物线对称轴上的一个动点,当的周长最小时,则点P的坐标为 .
三、解答题
17.已知抛物线的顶点坐标为,且经过点.
(1)求抛物线对应的函数表达式;
(2)当时,求函数的最大值.
18.某数学兴趣小组在暑假开展社会实践活动,销售某品牌书包,平均每天可以销售20个,每个盈利12元,为了扩大销售,增加盈利,该小组决定采取适当的降价措施,经调查发现,如果每个书包每降价1元,平均每天可以多卖5个.
(1)若该兴趣小组同学想要一天盈利300元,每个书包应降价多少元;
(2)该兴趣小组同学想要一天盈利最大,应降价多少元,所得最大利润是多少元?
19.如图,抛物线与x轴交于A、B两点,与y轴交于点C.
(1)结合函数图象,当时,直接写出y的取值范围:_____;
(2)若点M是直线下方抛物线上一动点,求四边形面积的最大值.
20.已知:如图,抛物线过点,且其对称轴为直线,点为抛物线上第二象限内一点.
(1)求二次函数的解析式;
(2)如图1,求面积的最大值;
(3)如图2,若抛物线上点的横坐标为,且的面积为,求点的坐标.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
题号 1 2 3 4 5 6 7 8
答案 C A B B B A C B
1.C
【分析】本题主要考查了二次函数的应用.先将二次函数一般式化为顶点式,再根据二次函数性质即可求解.
【详解】解:,
∵,,
∴当时,有最大值,最大值为45,
∴小球运动中的最大高度是.
故选:C.
2.A
【分析】本题主要考查了二次函数的的性质等知识点,根据函数的取值范围确定函数最小值出现在哪个函数上,然后再根据二次函数的性质即可得解,熟练掌握二次函数的性质是解决此题的关键.
【详解】解:∵函数,
∴当时,函数的最小值在函数上,
∴当时,该函数的最小值是3,
故选:A.
3.B
【分析】本题考查了二次函数的性质,二次函数的最值.利用抛物线解析式求得对称轴,即可求得函数的最小值,然后根据、的取值,判断的值,从而判断的大小.
【详解】解:解:由二次函数可知对称轴为直线,
函数的最小值,
若,,则,
,
若,,则,
,
故选项B正确,选项A、C、D错误.
故选:B.
4.B
【分析】本题考查了二次函数的最值问题,抛物线开口向上,在顶点处取得最小值,开口向下,二次函数在顶点处取得最大值.根据二次函数最值问题对各选项分析判断即可得解.
【详解】解:A、函数值3不是最小值,故本选项错误;
B、时有最小值3,故本选项正确;
C、时有最大值3,故本选项错误;
D、函数有最大值3,故本选项错误.
故选:B.
5.B
【分析】本题考查了二次函数的最值问题,整理出的表达式,考虑利用二次函数求解是解题的关键.
整理得到的表达式,再根据二次函数的最值问题和平方数非负数的性质解答.
【详解】解:∵,
,
,
,
当时,或,
∴当时,,
,
,
,
∴当时,有最大值4.
故选:B.
6.A
【分析】本题考查了二次函数的图象与系数的关系,二次函数的最值问题,在本题中分类讨论思想运用是解题的关键.先根据二次函数的已知条件,得出二次函数的图象开口向上,再分别进行讨论,即可得出函数的最大值与最小值即可得到结论.
【详解】解:二次函数,
该抛物线的对称轴为直线,且,
当,
当时,二次函数有最大值为:,即,
当时,二次函数有最小值为:,即,
当,
当时,二次函数有最大值为:,
当时,二次函数有最小值为:,即,
当,
此时当时,函数有最大值,
当时,函数有最小值,即,
,当时,函数有最大值,当时,函数有最小值,即,
,当或1时.函数有最大值,
当时,函数有最小值,即,
的值与有关,但与无关,
故选:.
7.C
【分析】本题考查了二次函数的图象与性质,二次函数的最值等知识.熟练掌握二次函数的图象与性质是解题的关键.
由,可知图象开口向上,对称轴为直线,顶点坐标为,当时,,即关于对称轴对称的点坐标为,由当时,函数取得最大值;当时,函数取得最小值,可得,计算求解,然后作答即可.
【详解】解:∵,
∴图象开口向上,对称轴为直线,顶点坐标为,
当时,,
∴关于对称轴对称的点坐标为,
∵当时,函数取得最大值;当时,函数取得最小值,
∴,
解得,,
故选:C.
8.B
【分析】本题主要考查了二次函数与一元二次方程之间的关系,二次函数与一次函数之间的关系,二次函数的性质等等,抛物线与x轴的交点的横坐标即为对应的一元二次方程的解,据此可判断①;根据增减性即可判断②;根据对称轴处函数有最大值即可判断③;直线与抛物线的交点的横坐标即为方程的根,求出根的情况即可判断④.
【详解】解:由函数图象可知,抛物线与x轴的两个交点坐标为,
∴一元二次方程的根为,故①正确;
∵抛物线开口向下,
∴离对称轴越远函数值越小,
∵抛物线对称轴为直线,且,
∴,故②错误;
当时,y有最大值,最大值为,
∴,即,故③正确;
根据题意可得直线与抛物线的交点的横坐标即为方程的根,
∵,
∴方程的根可以为或或,
∴对应的P的值有三个,故④错误;
故选:B.
9.
【分析】本题主要考查二次函数的应用,根据题意得出飞机滑行的距离即为s的最大值,将函数解析式配方成顶点式求出s的最大值即可得.
【详解】解:∵,
∴当时,取得最大值,即飞机着陆后滑行米才能停下来,
故答案为:.
10.
【分析】本题考查了二次函数的最值问题,先将解析式配方成顶点式,根据二次函数的增减性和最值问题解答.
【详解】解:,抛物线顶点坐标,开口向上,对称轴为直线,
∵时,函数y的最大值是6,最小值是2,
当函数值为2时,,
解得,
当函数值为6时,,
解得:或.
∴.
故答案为:.
11.1
【分析】本题考查了二次函数图象上点的坐标特征,二次函数的最值.代入点,得到,化简并配方,根据二次函数性质解答即可.
【详解】解:把代入二次函数中得,
,
∴
,
∵,
∴当时,有最小值,最小值为1.
故答案为:1.
12.8
【分析】本题考查了二次函数的最值及二次函数的图像上点的坐标特征,最后根据二次函数的性质求最值是解题的关键.
设点P的坐标为,,根据四边形的周长得到:,再由二次函数的性质即可求得最大值.
【详解】解:当,则,
解得:,
设点P的坐标为,,
由题意可知:四边形的周长,
∴,
∵,
当时,C有最大值8.
故答案为:8.
13.
【分析】此题考查了二次函数的性质,二次函数的最值,正确理解二次函数的性质是解题的关键.判断图象开口向下,顶点坐标为,结合,,可得当时,函数取最小值,再进一步可得答案.
【详解】解:∵,
∴图象开口向下,顶点坐标为,
∵,,
∵当时,函数有最小值,
∴当时,函数取最小值,最小值为:;
故答案为:.
14.
【分析】本题考查了二次函数的应用,把二次函数解析式转化为顶点式,求出二次函数的最大值即可求解,掌握配方法是解题的关键.
【详解】解:∵,
∴当时,有最大值为,
∴飞机着陆后滑行才能停下来,
故答案为:.
15. > 0或3.
【分析】本题考查了二次函数的图象性质,把点和代入进行计算,即可判断和;结合在时,随的增大而减小;在时,随的增大而增大,所以分类讨论:当时,则把代入,当时,把代入,进行计算即可作答.
【详解】解:∵二次函数,点和在函数图象上,
∴,,
∴;
∵函数,
∴二次函数的顶点坐标为,开口向上,
则在时,随的增大而减小;在时,随的增大而增大;
当时,函数的最小值为1,
∴当时,则把代入,
得,
解得(舍去),
∴当时,把代入,
得,
解得(舍去),
综上:的值为0或3.
故答案为:>,0或3.
16.
【分析】本题考查了用待定系数法求二次函数的解析式、轴对称的性质、一次函数;其中熟练运用轴对称的性质转化线段是解题的关键.根据抛物线的对称性可知:,所以当点在线段上时,的值最小,的周长也最小,以此为依据求解即可;
【详解】解:令,则,
解得,,
,,
抛物线的对称轴为:
点的横坐标为:
当 时, ;
设直线解析式为,
则,
解得,
由抛物线的对称性可知:
∴当点在线段上时,有最小值,则的周长最小,
将 代入得:
故此时点的坐标是
故答案为:.
17.(1)抛物线对应的函数表达式为
(2)在中,当时,有最大值为
【分析】本题考查二次函数综合,涉及待定系数法确定函数表达式、二次函数图象与性质求最值等知识,熟练掌握待定系数法确定函数表达式、二次函数图象与性质求最值的方法是解决问题的关键.
(1)根据题意,设出二次函数顶点式,利用待定系数法确定函数表达式即可得到答案;
(2)由(1)中所求表达式,利用二次函数图象与性质即可求出当时,函数的最大值.
【详解】(1)解:抛物线的顶点坐标为,
设函数表达式为,
把代入得:,
解得:,
抛物线对应的函数表达式为;
(2)解:由(1)知抛物线对应的函数表达式为,
抛物线开口向上、对称轴为,
当时,随的增大而增大,
在中,当时,有最大值为.
18.(1)元或元
(2)元,元
【分析】(1)设每个书包应降价元,则每个书包盈利元,平均每天可售出个,根据“数学兴趣小组每天销售该品牌书包获得的总利润每个书包的销售利润每天的销售量”,即可得出关于的一元二次方程,解之即可得出的值,进而得出结论;
(2)设每个书包降价元,则每个书包盈利元,平均每天可售出个,设每天盈利为元,根据“数学兴趣小组每天销售该品牌书包获得的总利润每个书包的销售利润每天的销售量”,即可得出关于的二次函数,求该二次函数的最值,即可得出结论.
【详解】(1)解:设每个书包应降价元,则每个书包盈利元,平均每天可售出个,
依题意可得:,
整理,得:,
解得:,,
每个书包应降价元或元;
(2)解:设每个书包降价元,则每个书包盈利元,平均每天可售出个,设每天盈利为元,
依题意可得:,
整理,得:,
,
抛物线开口向下,
当时,取得最大值,最大值为,
答:该兴趣小组同学想要一天盈利最大,应降价元,所得最大利润是元.
【点睛】本题主要考查了一元二次方程的应用(营销问题),因式分解法解一元二次方程,实际问题与二次函数(销售问题),把化成顶点式,二次函数的图象与系数的关系,二次函数的最值等知识点,根据“数学兴趣小组每天销售该品牌书包获得的总利润每个书包的销售利润每天的销售量”正确列出一元二次方程或二次函数解析式是解题的关键.
19.(1)
(2)四边形面积的最大值为4.
【分析】(1)根据抛物线解析式求得当和时y的值,再结合函数图象作答即可;
(2)过点M作轴于点N,连接,设点,则,,根据构建二次函数,利用二次函数的性质求出最大值即可解决问题.
【详解】(1)解:对于,
令,则,即,
令,则,
由函数图象知,当时,y的取值范围为,
故答案为:.
(2)如图,过点M作轴于点N,连接,
令,则,
解得:,
,
设,则,,
,
,
,
,
当时,有最大值为4,
四边形面积的最大值为4.
【点睛】本题考查了抛物线与x轴的交点、二次函数的图象与性质、二次函数的面积问题、二次函数的最值问题,解题的关键是灵活运用所学知识解决问题,学会构建二次函数解决最值问题.
20.(1)
(2)12
(3)点的坐标为
【分析】本题考查待定系数法求函数解析式、二次函数的图象与性质、坐标与图形,正确求得函数表达式是解答的关键.
(1)先求得抛物线与x轴的另一个交点坐标,然后利用待定系数法求解即可;
(2)先求得直线的解析式为,过点做轴的垂线分别交抛物线于点,交轴于点.设点,则点,由,结二次函数的性质求解即可;
(3)先求得点D坐标,连接,则轴.过点做交轴于点.根据等底等高的三角形面积相等得到,进而求得点N坐标和直线的解析式为.联立方程组求解即可.
【详解】(1)解:抛物线过点,且其对称轴为直线
抛物线过点
设二次函数的解析式为,
把代入,得:.
二次函数的解析式为;
(2)解:设的解析式为,把点代入,得.
的解析式为.
如图,过点做轴的垂线分别交抛物线于点,交轴于点.
设点,
则点
,
∵,
面积的最大值为12.
(3)解:点的横坐标为,
,直线的解析式为.
连接,则轴.过点做交轴于点.则
.
,
,则点的坐标为,
,直线的解析式为,
直线的解析式为.
点为抛物线与直线的在第二象限内的交点,
解方程组,解得或(舍去)
点的坐标为.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
