湖南省邵阳市邵阳县石齐学校2015-2016学年八年级下学期第一次月考数学试题(平行班)
文档属性
| 名称 | 湖南省邵阳市邵阳县石齐学校2015-2016学年八年级下学期第一次月考数学试题(平行班) |  | |
| 格式 | zip | ||
| 文件大小 | 89.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-30 17:27:57 | ||
图片预览

文档简介
八年级下册第一次月考平行班数学试卷
时间:90分钟 满分:120分
一、选择题(本题共10小题,每小题3分,共30分)
1.下列图案中,不是中心对称图形的是( )
2.Rt△ABC中,∠C=90°,∠B=54° ,则∠A=( )
A.66° B.36° C.56° D.46°
3.下列几组数中,能作为直角三角形三边长度的是 ( )
A. 4,5,6 B.1,,2 C. 6,8,11 D. 5,12,23
4.用两块完全相同的直角三角形拼下列图形 ( http: / / www.21cnjy.com ):①平行四边形 ②矩形 ③菱形 ④正方形 ⑤等腰三角形 ⑥等边三角形,一定能拼成的图形是( )
A、①④⑤ B、②⑤⑥ C、①②⑤ D、①②③
5. 已知一个多边形的内角和是540°,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
6.在□ABCD中,∠A:∠B:∠C:∠D 的值可以是 ( )
A. 1:2:2:1 B.1:2:3:4 C.2:1:1:2 D. 2:1:2:1
在△ABC中,AB=BC=AC=6,则△ABC的面积为 ( )
A.9 B.18 C. D.
8.矩形、菱形、正方形都具有的性质是( )
A.对角线相等 B.对角线互相垂直 C.对角线互相平分 D.对角线平分对角
9.如果三角形的两条边分别为8和6,那么连接该三角形三边中点所得的周长可能是下列数据中的( )
A.8 B.10 C.14 D.16
在△ABC中,∠C=90°,角平分线AD交BC于点D,若BC=32,
BD∶CD=9∶7,则D点到AB边的距离为( )
A .18 B. 16 C. 14 D. 12
二、填空题(本题共8小题,每小题3分,共24分)
11.一个多边形的每个外角都是36°,这个多边形的内角和是 .
12.在□ABCD中,∠A+∠C=120°,则∠B= .
13.在Rt△ABC中,∠ACB=90°,D是AB的中点,CD=4 cm,则AB=________cm.
14.将一副三角板按如图所示的方式叠放,则角α= 。
15.有三个内角是直角的四边形是 ;对角线互相垂直平分的四边形是 .
16.正方形ABCD的周长为8cm,顺次连接正方形ABCD各边的中点得到四边形EFGH,则四边形EFGH的周长等于 ;面积等于 .
17. 矩形两条对角线夹角为60°且对角线长为4, 则矩形较长边的长是 .
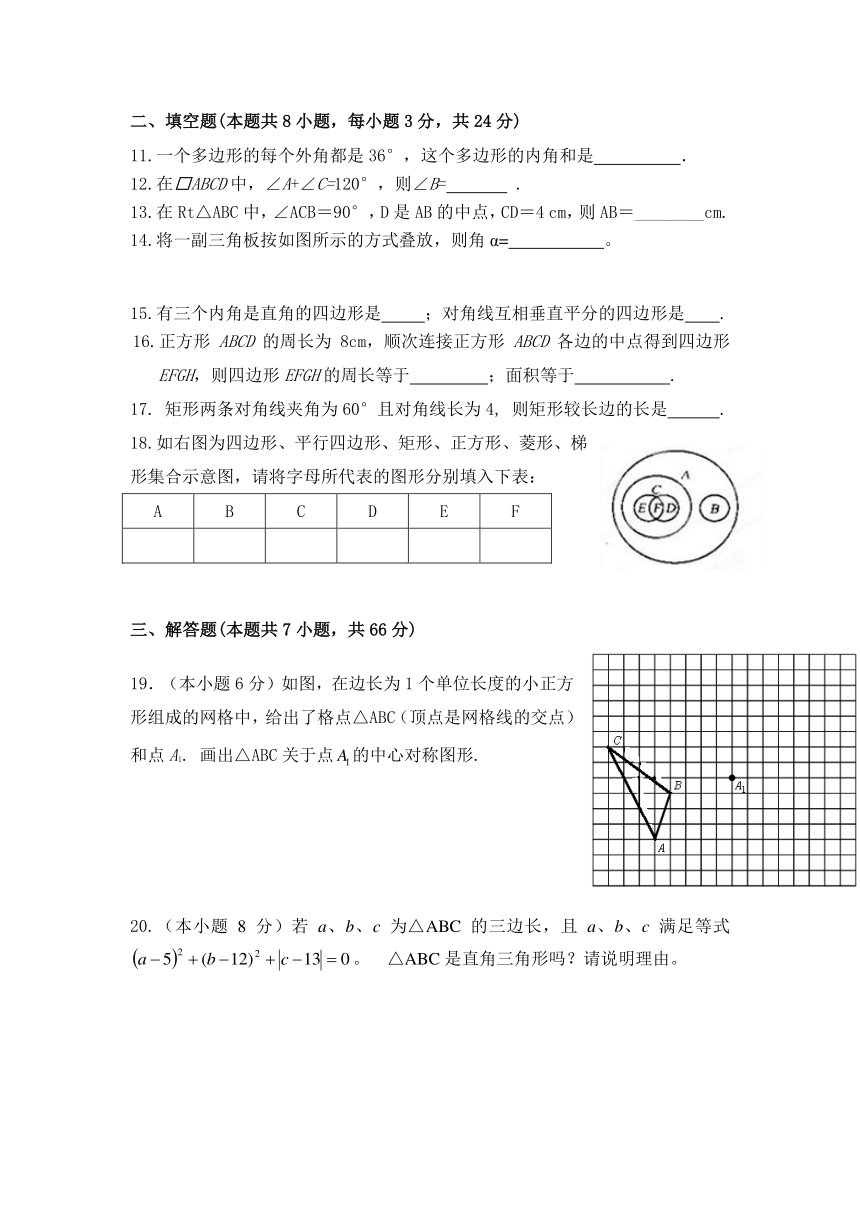
18.如右图为四边形、平行四边形、矩形、正方形、菱形、梯形集合示意图,请将字母所代表的图形分别填入下表:
A B C D E F
解答题(本题共7小题,共66分)
19.(本小题6分)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1. 画出△ABC关于点的中心对称图形.
20.(本小题8分)若a、b、c为△ABC的三边长,且a、b、c满足等式。 △ABC是直角三角形吗?请说明理由。
(本小题8分)已知:E、F是平行四边行ABCD的对角线AC上的两点,AE=CF。
求证:∠CDF=∠ABE
22.(本小题满分10分)如图所示,E 、 F 、G 、 H是矩形ABCD的四边中点,
求证:四边形EFGH是菱形.
24.(本小题10分)如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF,∠CAE=30°.求∠ACF的度数.
25.(本小题12分)已知:如图,为了躲避海盗,一轮船一直由西向东航行,早上8点,在A处测得小岛P的方向是北偏东75°,以每小时15海里的速度继续向东航行,10点到达B处,并测得小岛P的方向是北偏东60°,若小岛周围25海里内有暗礁,问该轮船一直向东航行是否有触礁的危险?
25.(本小题12分)如图,已知锐角△AB ( http: / / www.21cnjy.com )C中,以AB,AC为边向外作正方形ABDE和正方形ACFG,连结CE、BG,交点为O,求证:(1)EC=BG;(2)EC⊥BG.
八年级下册平行班第一次月考数学试卷参考答案
1-5 BBBCB 6-10 DCCBC
12. 13.8 14.
矩形;菱形 16., 17.
A B C D E F
四边形 梯形 平行四边形 矩形 菱形 正方形
18.
注:(D矩形和E菱形可交换位置)
略
21.证明△CDF△ABE即可得。
22.证明四个直角三角形全等得HE=EF=FG=GH.所以四边形EFGH是菱形
23.
24.过点P向AB的延长线作垂线,垂足为Q求得PQ=15海里<25海里,所以该轮船一 直向东航行有触礁的危险。
25.证明(1)在正方形ABDE和正方形ACFG中,
AE=AB,AC=AG, (2)由(1)知:△EAC≌△BAG,
∠EAB=∠GAC=90°, ∴∠AEC=∠ABG.
∴∠EAB+∠BAC=∠GAC+∠BAC. 又∵∠1=∠2,
即∠EAC=∠BAG, ∴∠ABG+∠2=∠AEC+∠1=90°.
∴△EAC≌△BAG. ∴∠EOB=∠EAB=90°∴EC⊥BG
∴EC=BG.
姓名___________________ 班级________________ 考号________________
…………………………………………………………………………………………………………………………………………
A
B
C
D
HA
A
EA
BA
FA
DCA
GA
CA
北x北
60°
B
75°
东
P
A
时间:90分钟 满分:120分
一、选择题(本题共10小题,每小题3分,共30分)
1.下列图案中,不是中心对称图形的是( )
2.Rt△ABC中,∠C=90°,∠B=54° ,则∠A=( )
A.66° B.36° C.56° D.46°
3.下列几组数中,能作为直角三角形三边长度的是 ( )
A. 4,5,6 B.1,,2 C. 6,8,11 D. 5,12,23
4.用两块完全相同的直角三角形拼下列图形 ( http: / / www.21cnjy.com ):①平行四边形 ②矩形 ③菱形 ④正方形 ⑤等腰三角形 ⑥等边三角形,一定能拼成的图形是( )
A、①④⑤ B、②⑤⑥ C、①②⑤ D、①②③
5. 已知一个多边形的内角和是540°,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
6.在□ABCD中,∠A:∠B:∠C:∠D 的值可以是 ( )
A. 1:2:2:1 B.1:2:3:4 C.2:1:1:2 D. 2:1:2:1
在△ABC中,AB=BC=AC=6,则△ABC的面积为 ( )
A.9 B.18 C. D.
8.矩形、菱形、正方形都具有的性质是( )
A.对角线相等 B.对角线互相垂直 C.对角线互相平分 D.对角线平分对角
9.如果三角形的两条边分别为8和6,那么连接该三角形三边中点所得的周长可能是下列数据中的( )
A.8 B.10 C.14 D.16
在△ABC中,∠C=90°,角平分线AD交BC于点D,若BC=32,
BD∶CD=9∶7,则D点到AB边的距离为( )
A .18 B. 16 C. 14 D. 12
二、填空题(本题共8小题,每小题3分,共24分)
11.一个多边形的每个外角都是36°,这个多边形的内角和是 .
12.在□ABCD中,∠A+∠C=120°,则∠B= .
13.在Rt△ABC中,∠ACB=90°,D是AB的中点,CD=4 cm,则AB=________cm.
14.将一副三角板按如图所示的方式叠放,则角α= 。
15.有三个内角是直角的四边形是 ;对角线互相垂直平分的四边形是 .
16.正方形ABCD的周长为8cm,顺次连接正方形ABCD各边的中点得到四边形EFGH,则四边形EFGH的周长等于 ;面积等于 .
17. 矩形两条对角线夹角为60°且对角线长为4, 则矩形较长边的长是 .
18.如右图为四边形、平行四边形、矩形、正方形、菱形、梯形集合示意图,请将字母所代表的图形分别填入下表:
A B C D E F
解答题(本题共7小题,共66分)
19.(本小题6分)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1. 画出△ABC关于点的中心对称图形.
20.(本小题8分)若a、b、c为△ABC的三边长,且a、b、c满足等式。 △ABC是直角三角形吗?请说明理由。
(本小题8分)已知:E、F是平行四边行ABCD的对角线AC上的两点,AE=CF。
求证:∠CDF=∠ABE
22.(本小题满分10分)如图所示,E 、 F 、G 、 H是矩形ABCD的四边中点,
求证:四边形EFGH是菱形.
24.(本小题10分)如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF,∠CAE=30°.求∠ACF的度数.
25.(本小题12分)已知:如图,为了躲避海盗,一轮船一直由西向东航行,早上8点,在A处测得小岛P的方向是北偏东75°,以每小时15海里的速度继续向东航行,10点到达B处,并测得小岛P的方向是北偏东60°,若小岛周围25海里内有暗礁,问该轮船一直向东航行是否有触礁的危险?
25.(本小题12分)如图,已知锐角△AB ( http: / / www.21cnjy.com )C中,以AB,AC为边向外作正方形ABDE和正方形ACFG,连结CE、BG,交点为O,求证:(1)EC=BG;(2)EC⊥BG.
八年级下册平行班第一次月考数学试卷参考答案
1-5 BBBCB 6-10 DCCBC
12. 13.8 14.
矩形;菱形 16., 17.
A B C D E F
四边形 梯形 平行四边形 矩形 菱形 正方形
18.
注:(D矩形和E菱形可交换位置)
略
21.证明△CDF△ABE即可得。
22.证明四个直角三角形全等得HE=EF=FG=GH.所以四边形EFGH是菱形
23.
24.过点P向AB的延长线作垂线,垂足为Q求得PQ=15海里<25海里,所以该轮船一 直向东航行有触礁的危险。
25.证明(1)在正方形ABDE和正方形ACFG中,
AE=AB,AC=AG, (2)由(1)知:△EAC≌△BAG,
∠EAB=∠GAC=90°, ∴∠AEC=∠ABG.
∴∠EAB+∠BAC=∠GAC+∠BAC. 又∵∠1=∠2,
即∠EAC=∠BAG, ∴∠ABG+∠2=∠AEC+∠1=90°.
∴△EAC≌△BAG. ∴∠EOB=∠EAB=90°∴EC⊥BG
∴EC=BG.
姓名___________________ 班级________________ 考号________________
…………………………………………………………………………………………………………………………………………
A
B
C
D
HA
A
EA
BA
FA
DCA
GA
CA
北x北
60°
B
75°
东
P
A
同课章节目录
