第十四章 勾股定理总复习
图片预览





文档简介
课件18张PPT。 第14章总复习
《勾股定理》 1. 了解勾股定理的内容和名字的由来, 并会用它来解决一些有关直角三角形的计算问题。 2.理解勾股定理常见的证明方法,并会 用这种思想来求一些图形面积问题。
3.会用勾股定理判断是否是一组勾股数。知识点目标4.理解勾股定理逆定理的含义,并会用它来判断一个三角形是否是直角三角形。
5.能区分和辨认勾股定理与勾股定理逆定理,并会简单的综合运用。
6.能用勾股定理解决生活中的实际问题。 一. 勾股定理
直角三角形两直角边的平方和等于斜边的平方.
注意:(1)直角三角形
(2)分清直角边和斜边
(3)反映的是三边关系
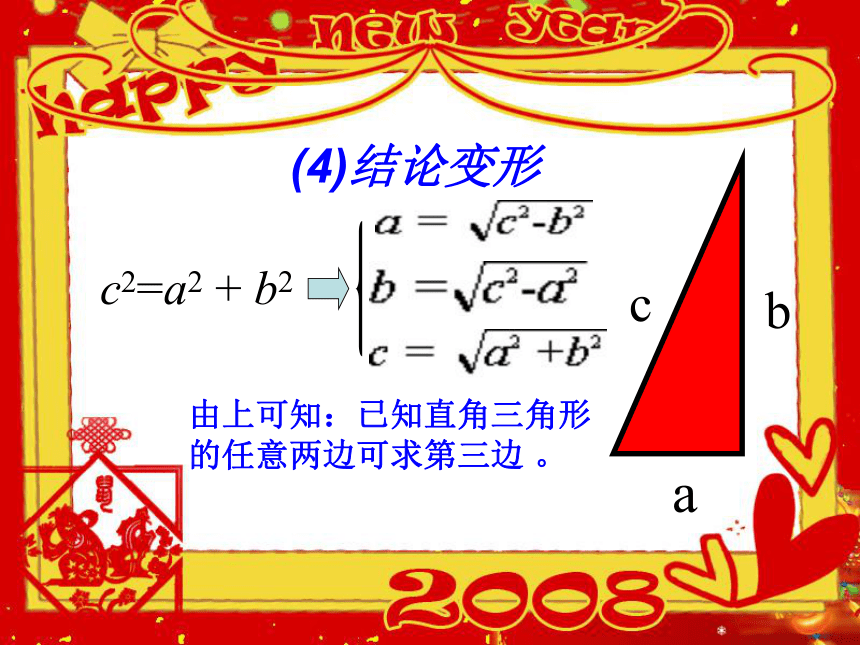
(4)结论变形c2=a2 + b2由上可知:已知直角三角形
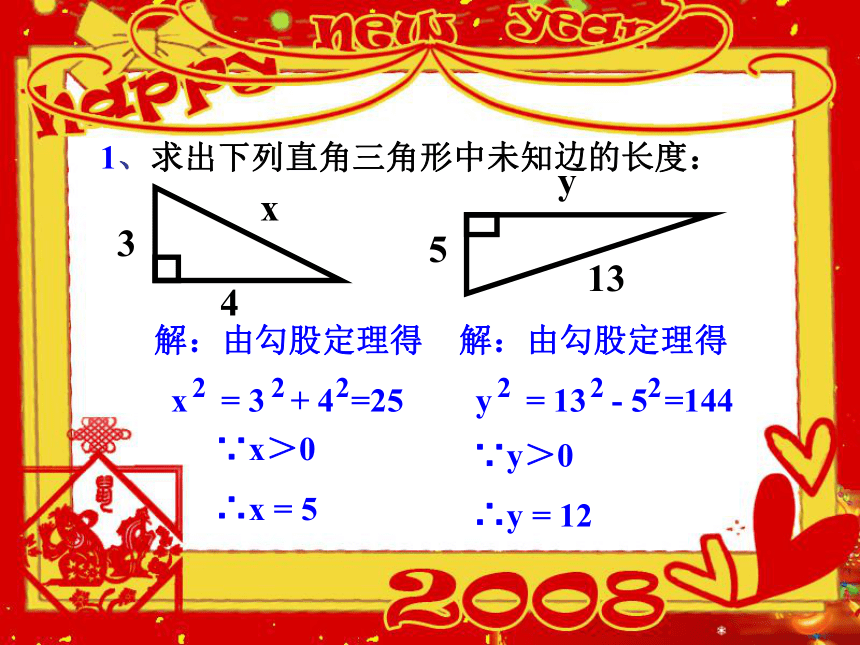
的任意两边可求第三边 。1、求出下列直角三角形中未知边的长度:∵x>0
∴x = 5解:由勾股定理得
y = 13 - 5 =144222∵y>0
∴y = 122.?ABC的两边AB=5,AC=12,则BC=13 ( )
1 . 对 2. 错
3.直角? ABC中∠B=90°,a=6,b=8,则c=10 ( ) 1 . 对 2. 错4、已知:数3和4,请你再写一个数,使这
些数恰好是一个直角三角形三边长,则这
个数可以是( )2 25.求下列阴影部分的面积:
(1)阴影部分是正方形( )
(2)阴影部分是长方形( )
(3)阴影部分是半圆( )PQR二、勾股定理证明方法:如图,分别以直角三角形的三边向外作正方形,正方形P、 Q、 R之间的面积关系acSP+SQ=SRPcb6、求下列字母所代表的正方形的面积。解:正方形A的面积
=66+144
=210 解:正方形B的面积
=225-81
=144 7、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形边长为9,求正方形A、B、C、D的面积和( )1、无法确定
2、45
3、81
4、90 38、如图,以Rt△ABC的三边为直径分别向外作三个半圆,则三个半圆的面积之间的关系是( ). PQRabc (2)不要与勾股定理混淆,勾股定理只适用在直角三角形中求边之间的关系!如果三角形的三边长a、b、c满足 a2+b2=c2,
那么这个三角形是直角三角形.三、勾股定理逆定理:注:(1)可用来证明一个角是直角或一个 三角形是直角三角形9判断:若“是”选1,若“不是”选2
(A)设三角形三边长分别为下列各组数,试判断各三角形是否是直角三角形
(1)7,12,20 ( ) (2)9,12,15( )
(3)12,16,20( )
判断的根据是( )211勾股定理的逆定理9(B)若a,b,c是一组勾股数,则3a,3b,3c也是一组勾股数吗?( )1四、勾股定理应用:
10、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(1)3 (2 )√ (3)2 (4)12511、如图三级台阶,每一级的长5cm 、宽3cm、
高1cm,一只蚂蚁从A点出发沿着台阶面爬到B点
去吃食物,请你想一想,最短线路是多少?D解: ∵ AB2=AC2+BC2=169,
∴ AB=13.
答:从A点爬到B点,最短线路是13.ABCD12、《九章算术》中记载了一道有趣的问题,意思是:有一个水池,水面是一边长为10尺的正方形,水池的中
央有一根芦苇,它高出水
面1尺,若把它拉向岸边,
它的顶端恰好达岸边水面,
问:水池的深度和芦苇的
长度各是多少?DABCAB =BC + AC222解:设水池的深度为X米,则芦苇高为 (X+1)米.
根据题意得:AB2=BC2+AC2
(X+1)2=52+X2
X2+2X+1=25+X2
X=12
X+1=12+1=13(米)
答:水池的深度为12米,
芦苇高为13米.DABC
《勾股定理》 1. 了解勾股定理的内容和名字的由来, 并会用它来解决一些有关直角三角形的计算问题。 2.理解勾股定理常见的证明方法,并会 用这种思想来求一些图形面积问题。
3.会用勾股定理判断是否是一组勾股数。知识点目标4.理解勾股定理逆定理的含义,并会用它来判断一个三角形是否是直角三角形。
5.能区分和辨认勾股定理与勾股定理逆定理,并会简单的综合运用。
6.能用勾股定理解决生活中的实际问题。 一. 勾股定理
直角三角形两直角边的平方和等于斜边的平方.
注意:(1)直角三角形
(2)分清直角边和斜边
(3)反映的是三边关系
(4)结论变形c2=a2 + b2由上可知:已知直角三角形
的任意两边可求第三边 。1、求出下列直角三角形中未知边的长度:∵x>0
∴x = 5解:由勾股定理得
y = 13 - 5 =144222∵y>0
∴y = 122.?ABC的两边AB=5,AC=12,则BC=13 ( )
1 . 对 2. 错
3.直角? ABC中∠B=90°,a=6,b=8,则c=10 ( ) 1 . 对 2. 错4、已知:数3和4,请你再写一个数,使这
些数恰好是一个直角三角形三边长,则这
个数可以是( )2 25.求下列阴影部分的面积:
(1)阴影部分是正方形( )
(2)阴影部分是长方形( )
(3)阴影部分是半圆( )PQR二、勾股定理证明方法:如图,分别以直角三角形的三边向外作正方形,正方形P、 Q、 R之间的面积关系acSP+SQ=SRPcb6、求下列字母所代表的正方形的面积。解:正方形A的面积
=66+144
=210 解:正方形B的面积
=225-81
=144 7、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形边长为9,求正方形A、B、C、D的面积和( )1、无法确定
2、45
3、81
4、90 38、如图,以Rt△ABC的三边为直径分别向外作三个半圆,则三个半圆的面积之间的关系是( ). PQRabc (2)不要与勾股定理混淆,勾股定理只适用在直角三角形中求边之间的关系!如果三角形的三边长a、b、c满足 a2+b2=c2,
那么这个三角形是直角三角形.三、勾股定理逆定理:注:(1)可用来证明一个角是直角或一个 三角形是直角三角形9判断:若“是”选1,若“不是”选2
(A)设三角形三边长分别为下列各组数,试判断各三角形是否是直角三角形
(1)7,12,20 ( ) (2)9,12,15( )
(3)12,16,20( )
判断的根据是( )211勾股定理的逆定理9(B)若a,b,c是一组勾股数,则3a,3b,3c也是一组勾股数吗?( )1四、勾股定理应用:
10、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(1)3 (2 )√ (3)2 (4)12511、如图三级台阶,每一级的长5cm 、宽3cm、
高1cm,一只蚂蚁从A点出发沿着台阶面爬到B点
去吃食物,请你想一想,最短线路是多少?D解: ∵ AB2=AC2+BC2=169,
∴ AB=13.
答:从A点爬到B点,最短线路是13.ABCD12、《九章算术》中记载了一道有趣的问题,意思是:有一个水池,水面是一边长为10尺的正方形,水池的中
央有一根芦苇,它高出水
面1尺,若把它拉向岸边,
它的顶端恰好达岸边水面,
问:水池的深度和芦苇的
长度各是多少?DABCAB =BC + AC222解:设水池的深度为X米,则芦苇高为 (X+1)米.
根据题意得:AB2=BC2+AC2
(X+1)2=52+X2
X2+2X+1=25+X2
X=12
X+1=12+1=13(米)
答:水池的深度为12米,
芦苇高为13米.DABC
