第30课时 欧姆定律相关计算 课件 2025年中考物理考点探究(湖南专版)(共22张ppt)
文档属性
| 名称 | 第30课时 欧姆定律相关计算 课件 2025年中考物理考点探究(湖南专版)(共22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-12-06 22:22:33 | ||
图片预览






文档简介
(共22张PPT)
第十三单元 欧姆定律
第30课时 欧姆定律相关计算
目录
CONTENTS
课时思维建构
1
知识点梳理
2
课堂检测
3
01
课时思维构建
02
知识点梳理
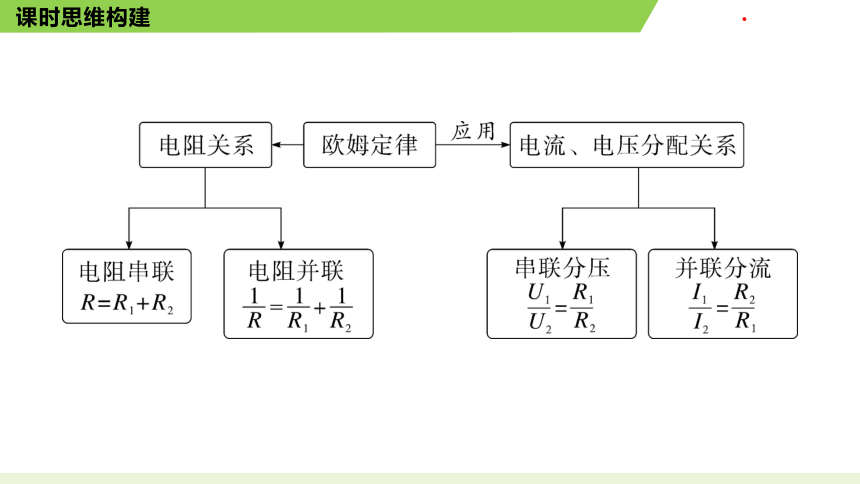
1. 串联电路分析
2. 并联电路分析
方法指导 电阻变化的动态电路分析与计算
例1 (2024·长沙)小明制作了一款可调亮度的小台灯,电路如图所示。电源电压保持不变,灯泡的电阻为10Ω,不考虑温度对灯丝电阻的影响,滑动变阻器标有“20Ω 1A”字样。
(1)闭合开关后,移动滑片使R的阻值变 时,
通过灯泡的电流变大,灯泡变亮。
小
(2)当滑动变阻器R接入电路的阻值最大时,通过灯泡的电流为0.15A,此时灯泡两端的电压为 V。若灯泡两端允许的最大电压为2.5V,为保证电路安全,滑动变阻器接入电路的最小阻值为 Ω。
1.5
8
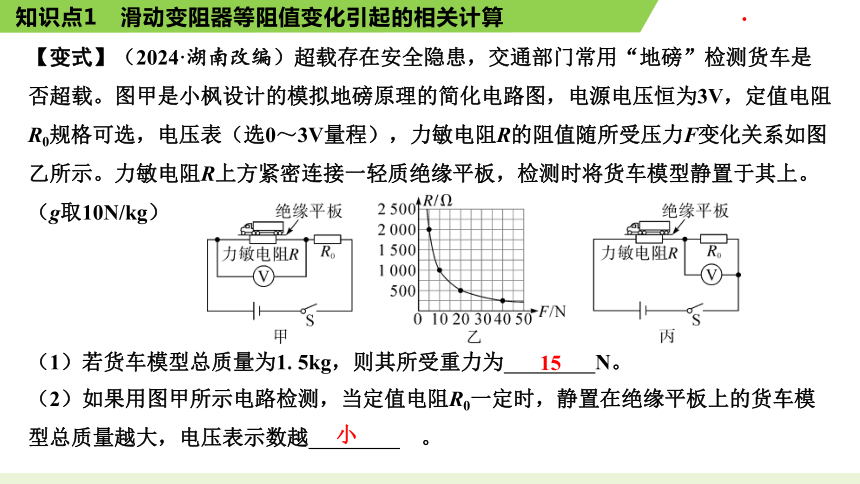
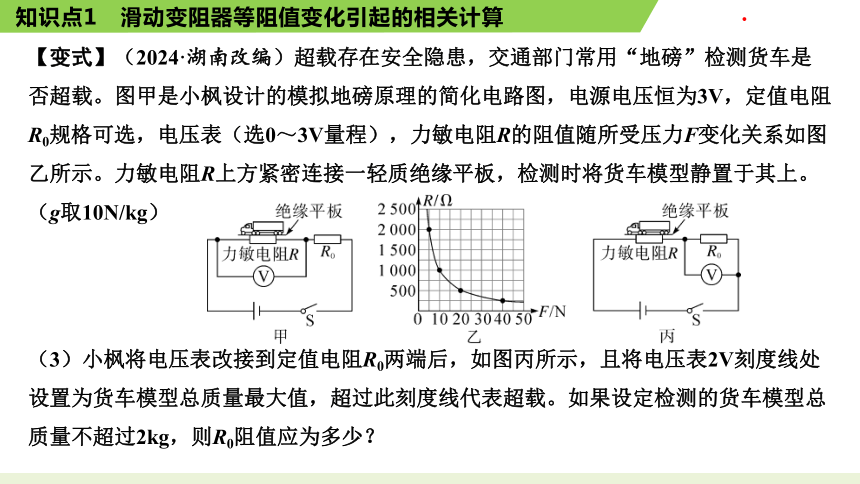
【变式】(2024·湖南改编)超载存在安全隐患,交通部门常用“地磅”检测货车是否超载。图甲是小枫设计的模拟地磅原理的简化电路图,电源电压恒为3V,定值电阻R0规格可选,电压表(选0~3V量程),力敏电阻R的阻值随所受压力F变化关系如图乙所示。力敏电阻R上方紧密连接一轻质绝缘平板,检测时将货车模型静置于其上。(g取10N/kg)
(1)若货车模型总质量为1.5kg,则其所受重力为 N。
(2)如果用图甲所示电路检测,当定值电阻R0一定时,静置在绝缘平板上的货车模型总质量越大,电压表示数越 。
15
小
(3)小枫将电压表改接到定值电阻R0两端后,如图丙所示,且将电压表2V刻度线处设置为货车模型总质量最大值,超过此刻度线代表超载。如果设定检测的货车模型总质量不超过2kg,则R0阻值应为多少?
【变式】(2024·湖南改编)超载存在安全隐患,交通部门常用“地磅”检测货车是否超载。图甲是小枫设计的模拟地磅原理的简化电路图,电源电压恒为3V,定值电阻R0规格可选,电压表(选0~3V量程),力敏电阻R的阻值随所受压力F变化关系如图乙所示。力敏电阻R上方紧密连接一轻质绝缘平板,检测时将货车模型静置于其上。(g取10N/kg)
解:由图丙可知,R0与R串联,电压
表与R0并联,当货车模型总质量为
2kg时,则其所受重力:G=mg=2kg×10N/kg=20N,
由图乙可知,此时力敏电阻R的电阻为500Ω,由题意知,将电压表2V刻度线处设置
为货车模型总质量最大值,根据欧姆定律和串联分压可得:
I=,则R0=×R=2×500Ω=1000Ω。
(3)小枫将电压表改接到定值电阻R0两端后,如图丙所示,且将电压表2V刻度线处设置为货车模型总质量最大值,超过此刻度线代表超载。如果设定检测的货车模型总质量不超过2kg,则R0阻值应为多少?
例2 两个电阻元件甲和乙通过它们的电流与它们两端电压的关系如图所示,将甲、乙串联接入某电路中,此时电路中的电流为0.2A。
(1)求电路中的总电阻R总。 (2)求电路中的电源电压。
解:(1)已知甲、乙串联,电流处处相等,根据欧姆定律
和图像可知,当电路中的电流为0.2A时,甲的电阻:
R甲==5Ω,乙的电阻:R乙==10Ω,
电路中的总电阻:R总=R甲+R乙=5Ω+10Ω=15Ω。
(2)此时电路中的电源电压:U=U甲+U乙=1V+2V=3V。
解:(3)根据图像可知,此时通过甲的电流I甲=
0.4A,通过乙的电流I乙=0.2A,干路电流:I=I甲+I乙
=0.4A+0.2A=0.6A。
解:(3)根据图像可知,此时通过甲的电流
I甲=0.4A,通过乙的电流I乙=0.2A,
干路电流:I=I甲+I乙=0.4A+0.2A=0.6A。
例2 两个电阻元件甲和乙通过它们的电流与它们两端电压的关系如图所示,将甲、乙串联接入某电路中,此时电路中的电流为0.2A。
(3)若将甲、乙并联在电源电压为2V的电路中,则干路电流
为多少?
第一步:判断电路连接方式和电表测量对象
第二步:分析电路限定条件
方法指导 极值、范围类计算解题思路
第三步:结合串并联电路特点、欧姆定律、电功率等求解其他量变化范围
例3 (2024·邵阳模拟)两个标有“5Ω 1A”和“10Ω 0.6A”字样的
定值电阻,在保证各元件安全的前提下,将它们串联起来使用,电源电
压最多为 V;若将它们并联,干路电流最大不得超过 A。
【变式】如图所示的电路中,R1=5Ω,滑动变阻器的规格为“20Ω
1A”,电源电压为4.5V并保持不变。电流表量程为0~0.6A,电压表量
程为0~3V。
(1)为保护电表,滑动变阻器阻值的变化范围为多少?
9
1.5
(1)由题意得,电路中的最大电流I大=0.6A,此时滑动变
阻器接入电路中的电阻最小,由欧姆定律可得电路中的总电
阻:R===7.5Ω,则滑动变阻器接入电路中的阻值
最小值:R2小=R-R1=7.5Ω-5Ω=2.5Ω;
(1)由题意得,电路中的最大电流I大=0.6A,此时滑动变阻器接入电路中的电阻最小,由欧姆定律可得电路中的总电阻:R==7.5Ω,则滑动变阻器接入电路中的阻值最小值:R2小=R-R1=7.5Ω-5Ω=2.5Ω;当电压表的示数U2=3V时,电路中的电流最小,滑动变阻器接入电路中的电阻最大,由串联电路电压规律可得,R1两端的电压:U1=U-U2=4.5V-3V=1.5V,则电路中的最小电流:I小=,即,解得:R2大=10Ω,所以,滑动变阻器阻值的变化范围为2.5~10Ω。
【变式】如图所示的电路中,R1=5Ω,滑动变阻器的规格为“20Ω 1A”,电源电压为4.5V并保持不变。电流表量程为0~0.6A,电压表量程为0~3V。
(1)为保护电表,滑动变阻器阻值的变化范围为多少?
【变式】如图所示的电路中,R1=5Ω,滑动变阻器的规格为“20Ω 1A”,电源电压为4.5V并保持不变。电流表量程为0~0.6A,电压表量程为0~3V。
(2)当滑动变阻器R2的阻值为8Ω时,电流表、电压表的示数
分别为多少?(结果保留两位小数)
解:由电路图可知,R1与R2串联,电压表测R2两端的电压,电流表测电路中的电流。
(2)由串联电路电阻规律可得,此时电路中电流表的示数:
I=A≈0.35A,则电压表的示数:U2'=IR2=A×8Ω≈2.78V。
03
课堂检测
1.如图所示电路的电源电压为1.5V,电阻R1的阻值为2Ω,闭合开关后,
电流表的示数为0.3A,则( D )
A. 通过R1的电流大于0.3A
B. 电阻R1和R2是并联的
C. 电压表的示数为0.9V
D. 电阻R2的阻值为3Ω
D
2.(2022·张家界)如图甲所示,电源电压保持不变,R1=10Ω,当闭合
开关S,滑动变阻器滑片P从a端移到b端时,两电表示数变化关系用图乙
中线段AB表示,则电源电压和滑动变阻器的最大阻值分别为( A )
A. 6V 20Ω
B. 4V 20Ω
C. 6V 10Ω
D. 4V 10Ω
A
3. (2023·郴州)如图所示,电阻R1、R2为定值电阻,电源电压保持不
变。当开关S1闭合,S2接a端时,电流表示数为I;当开关S1闭合,S2接b
端时,电流表示数为2I,则未知电阻Rx的阻值是( D )
A. R1+R2
B.
C. 2R1-R2
D. R1-2R2
D
4. 如图,这是某款医用红外线体温计的简化电路图,定值电阻R0=10Ω,电源电压U=3V,温度与热敏电阻的对应值关系如下表。当测量者体温超过37℃时,体温计就会发出提示声。
温度/℃ 15 25 37 38 40
热敏电阻/Ω 53 38 20 15 5
(1)当测量者的体温为
37℃时,求电路中的电流。
解:(1)由表格数据可知,当测量者的体温为37℃时,热敏电阻的阻值:R=20Ω,
由图可知热敏电阻R与定值电阻R0串联,由串联电路规律可得,
电路中的总电阻:R总=R+R0=20Ω+10Ω=30Ω,
由欧姆定律可得,电路中的电流:I==0.1A。
温度/℃ 15 25 37 38 40
热敏电阻/Ω 53 38 20 15 5
(2)当电压表的示数为1.8
V时,通过计算判断体温
计是否会发出提示声。
解:(2)当电压表的示数为UV=1.8V时,由串联电路电压规律可得,定值电阻两端的电压:U0=U-UV=3V-1.8V=1.2V,由欧姆定律可得,定值电阻中的电流:I0===0.12A,由串联电路的电流规律可得,电路中的电流:I'=I0=0.12A,已知37℃时电路中的电流大小:I=0.1A,分析题中表格数据可知,温度越高,热敏电阻的阻值越小,电路中的电流越大,因为I'>I,所以体温计此时的温度高于37℃,因此体温计会发出提示声。
第十三单元 欧姆定律
第30课时 欧姆定律相关计算
目录
CONTENTS
课时思维建构
1
知识点梳理
2
课堂检测
3
01
课时思维构建
02
知识点梳理
1. 串联电路分析
2. 并联电路分析
方法指导 电阻变化的动态电路分析与计算
例1 (2024·长沙)小明制作了一款可调亮度的小台灯,电路如图所示。电源电压保持不变,灯泡的电阻为10Ω,不考虑温度对灯丝电阻的影响,滑动变阻器标有“20Ω 1A”字样。
(1)闭合开关后,移动滑片使R的阻值变 时,
通过灯泡的电流变大,灯泡变亮。
小
(2)当滑动变阻器R接入电路的阻值最大时,通过灯泡的电流为0.15A,此时灯泡两端的电压为 V。若灯泡两端允许的最大电压为2.5V,为保证电路安全,滑动变阻器接入电路的最小阻值为 Ω。
1.5
8
【变式】(2024·湖南改编)超载存在安全隐患,交通部门常用“地磅”检测货车是否超载。图甲是小枫设计的模拟地磅原理的简化电路图,电源电压恒为3V,定值电阻R0规格可选,电压表(选0~3V量程),力敏电阻R的阻值随所受压力F变化关系如图乙所示。力敏电阻R上方紧密连接一轻质绝缘平板,检测时将货车模型静置于其上。(g取10N/kg)
(1)若货车模型总质量为1.5kg,则其所受重力为 N。
(2)如果用图甲所示电路检测,当定值电阻R0一定时,静置在绝缘平板上的货车模型总质量越大,电压表示数越 。
15
小
(3)小枫将电压表改接到定值电阻R0两端后,如图丙所示,且将电压表2V刻度线处设置为货车模型总质量最大值,超过此刻度线代表超载。如果设定检测的货车模型总质量不超过2kg,则R0阻值应为多少?
【变式】(2024·湖南改编)超载存在安全隐患,交通部门常用“地磅”检测货车是否超载。图甲是小枫设计的模拟地磅原理的简化电路图,电源电压恒为3V,定值电阻R0规格可选,电压表(选0~3V量程),力敏电阻R的阻值随所受压力F变化关系如图乙所示。力敏电阻R上方紧密连接一轻质绝缘平板,检测时将货车模型静置于其上。(g取10N/kg)
解:由图丙可知,R0与R串联,电压
表与R0并联,当货车模型总质量为
2kg时,则其所受重力:G=mg=2kg×10N/kg=20N,
由图乙可知,此时力敏电阻R的电阻为500Ω,由题意知,将电压表2V刻度线处设置
为货车模型总质量最大值,根据欧姆定律和串联分压可得:
I=,则R0=×R=2×500Ω=1000Ω。
(3)小枫将电压表改接到定值电阻R0两端后,如图丙所示,且将电压表2V刻度线处设置为货车模型总质量最大值,超过此刻度线代表超载。如果设定检测的货车模型总质量不超过2kg,则R0阻值应为多少?
例2 两个电阻元件甲和乙通过它们的电流与它们两端电压的关系如图所示,将甲、乙串联接入某电路中,此时电路中的电流为0.2A。
(1)求电路中的总电阻R总。 (2)求电路中的电源电压。
解:(1)已知甲、乙串联,电流处处相等,根据欧姆定律
和图像可知,当电路中的电流为0.2A时,甲的电阻:
R甲==5Ω,乙的电阻:R乙==10Ω,
电路中的总电阻:R总=R甲+R乙=5Ω+10Ω=15Ω。
(2)此时电路中的电源电压:U=U甲+U乙=1V+2V=3V。
解:(3)根据图像可知,此时通过甲的电流I甲=
0.4A,通过乙的电流I乙=0.2A,干路电流:I=I甲+I乙
=0.4A+0.2A=0.6A。
解:(3)根据图像可知,此时通过甲的电流
I甲=0.4A,通过乙的电流I乙=0.2A,
干路电流:I=I甲+I乙=0.4A+0.2A=0.6A。
例2 两个电阻元件甲和乙通过它们的电流与它们两端电压的关系如图所示,将甲、乙串联接入某电路中,此时电路中的电流为0.2A。
(3)若将甲、乙并联在电源电压为2V的电路中,则干路电流
为多少?
第一步:判断电路连接方式和电表测量对象
第二步:分析电路限定条件
方法指导 极值、范围类计算解题思路
第三步:结合串并联电路特点、欧姆定律、电功率等求解其他量变化范围
例3 (2024·邵阳模拟)两个标有“5Ω 1A”和“10Ω 0.6A”字样的
定值电阻,在保证各元件安全的前提下,将它们串联起来使用,电源电
压最多为 V;若将它们并联,干路电流最大不得超过 A。
【变式】如图所示的电路中,R1=5Ω,滑动变阻器的规格为“20Ω
1A”,电源电压为4.5V并保持不变。电流表量程为0~0.6A,电压表量
程为0~3V。
(1)为保护电表,滑动变阻器阻值的变化范围为多少?
9
1.5
(1)由题意得,电路中的最大电流I大=0.6A,此时滑动变
阻器接入电路中的电阻最小,由欧姆定律可得电路中的总电
阻:R===7.5Ω,则滑动变阻器接入电路中的阻值
最小值:R2小=R-R1=7.5Ω-5Ω=2.5Ω;
(1)由题意得,电路中的最大电流I大=0.6A,此时滑动变阻器接入电路中的电阻最小,由欧姆定律可得电路中的总电阻:R==7.5Ω,则滑动变阻器接入电路中的阻值最小值:R2小=R-R1=7.5Ω-5Ω=2.5Ω;当电压表的示数U2=3V时,电路中的电流最小,滑动变阻器接入电路中的电阻最大,由串联电路电压规律可得,R1两端的电压:U1=U-U2=4.5V-3V=1.5V,则电路中的最小电流:I小=,即,解得:R2大=10Ω,所以,滑动变阻器阻值的变化范围为2.5~10Ω。
【变式】如图所示的电路中,R1=5Ω,滑动变阻器的规格为“20Ω 1A”,电源电压为4.5V并保持不变。电流表量程为0~0.6A,电压表量程为0~3V。
(1)为保护电表,滑动变阻器阻值的变化范围为多少?
【变式】如图所示的电路中,R1=5Ω,滑动变阻器的规格为“20Ω 1A”,电源电压为4.5V并保持不变。电流表量程为0~0.6A,电压表量程为0~3V。
(2)当滑动变阻器R2的阻值为8Ω时,电流表、电压表的示数
分别为多少?(结果保留两位小数)
解:由电路图可知,R1与R2串联,电压表测R2两端的电压,电流表测电路中的电流。
(2)由串联电路电阻规律可得,此时电路中电流表的示数:
I=A≈0.35A,则电压表的示数:U2'=IR2=A×8Ω≈2.78V。
03
课堂检测
1.如图所示电路的电源电压为1.5V,电阻R1的阻值为2Ω,闭合开关后,
电流表的示数为0.3A,则( D )
A. 通过R1的电流大于0.3A
B. 电阻R1和R2是并联的
C. 电压表的示数为0.9V
D. 电阻R2的阻值为3Ω
D
2.(2022·张家界)如图甲所示,电源电压保持不变,R1=10Ω,当闭合
开关S,滑动变阻器滑片P从a端移到b端时,两电表示数变化关系用图乙
中线段AB表示,则电源电压和滑动变阻器的最大阻值分别为( A )
A. 6V 20Ω
B. 4V 20Ω
C. 6V 10Ω
D. 4V 10Ω
A
3. (2023·郴州)如图所示,电阻R1、R2为定值电阻,电源电压保持不
变。当开关S1闭合,S2接a端时,电流表示数为I;当开关S1闭合,S2接b
端时,电流表示数为2I,则未知电阻Rx的阻值是( D )
A. R1+R2
B.
C. 2R1-R2
D. R1-2R2
D
4. 如图,这是某款医用红外线体温计的简化电路图,定值电阻R0=10Ω,电源电压U=3V,温度与热敏电阻的对应值关系如下表。当测量者体温超过37℃时,体温计就会发出提示声。
温度/℃ 15 25 37 38 40
热敏电阻/Ω 53 38 20 15 5
(1)当测量者的体温为
37℃时,求电路中的电流。
解:(1)由表格数据可知,当测量者的体温为37℃时,热敏电阻的阻值:R=20Ω,
由图可知热敏电阻R与定值电阻R0串联,由串联电路规律可得,
电路中的总电阻:R总=R+R0=20Ω+10Ω=30Ω,
由欧姆定律可得,电路中的电流:I==0.1A。
温度/℃ 15 25 37 38 40
热敏电阻/Ω 53 38 20 15 5
(2)当电压表的示数为1.8
V时,通过计算判断体温
计是否会发出提示声。
解:(2)当电压表的示数为UV=1.8V时,由串联电路电压规律可得,定值电阻两端的电压:U0=U-UV=3V-1.8V=1.2V,由欧姆定律可得,定值电阻中的电流:I0===0.12A,由串联电路的电流规律可得,电路中的电流:I'=I0=0.12A,已知37℃时电路中的电流大小:I=0.1A,分析题中表格数据可知,温度越高,热敏电阻的阻值越小,电路中的电流越大,因为I'>I,所以体温计此时的温度高于37℃,因此体温计会发出提示声。
同课章节目录
