北师大版2024-2025学年数学八年级上册期末重难点真题检测卷(含解析)
文档属性
| 名称 | 北师大版2024-2025学年数学八年级上册期末重难点真题检测卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 588.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 08:45:07 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
期末重难点真题检测卷-2024-2025学年数学八年级上册北师大版
一.选择题(共10小题)
1.(2023秋 二道区校级期末)9的平方根是( )
A.±3 B.3 C. D.
2.(2023秋 婺城区期末)能说明“三角形的高线一定在三角形的内部(含边界)”是假命题的反例是( )
A. B.
C. D.
3.(2023秋 伊川县期末)直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )
A.121 B.120 C.90 D.不能确定
4.(2023秋 伊川县期末)如图,是某企业1~5月份利润的折线统计图,根据图中信息,下列说法错误的是( )
A.利润最高是130万
B.利润最低是100万
C.利润增长最快的是2~3月份
D.利润增长最快的是4~5月份
5.(2022秋 沈河区期末)估计的值在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
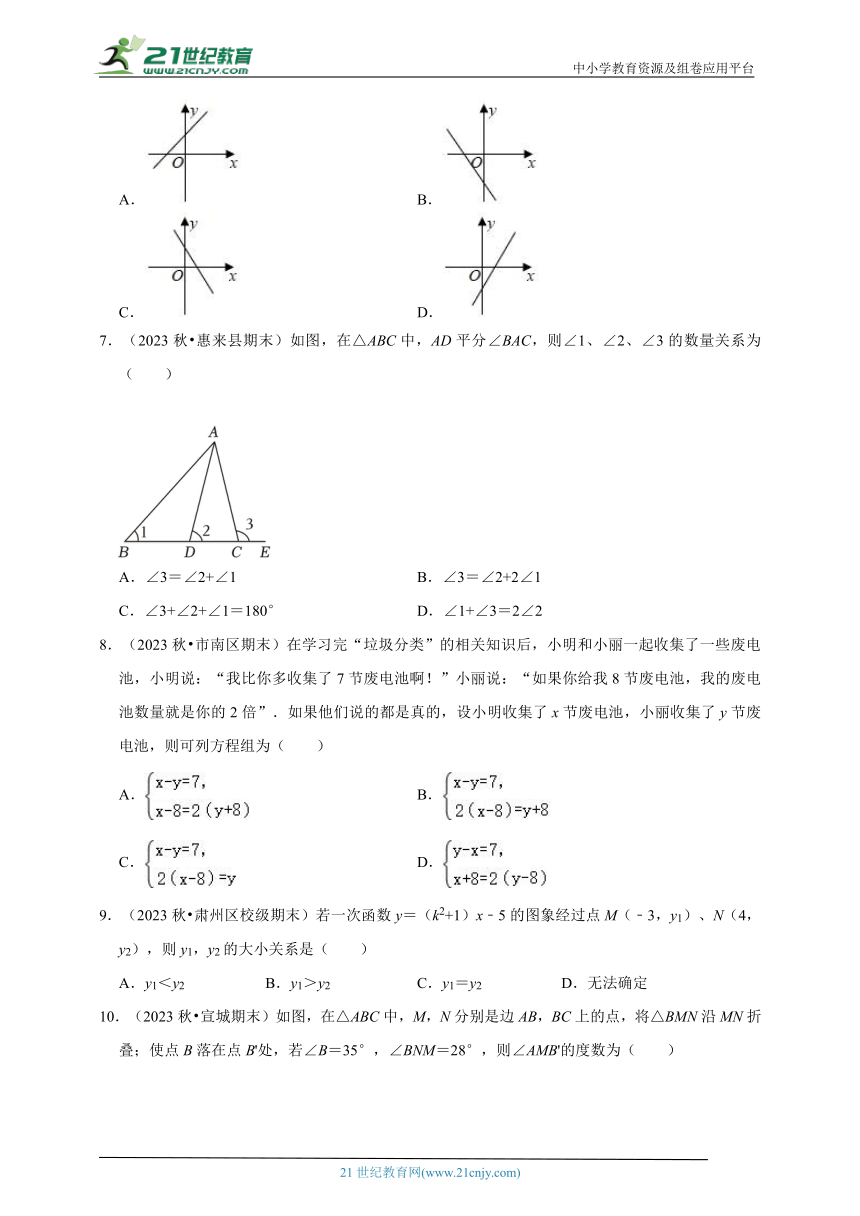
6.(2024春 吐鲁番市期末)已知一次函数y=kx+2(k≠0)的函数值y随x的增大而增大,则该函数的图象大致是( )
A. B.
C. D.
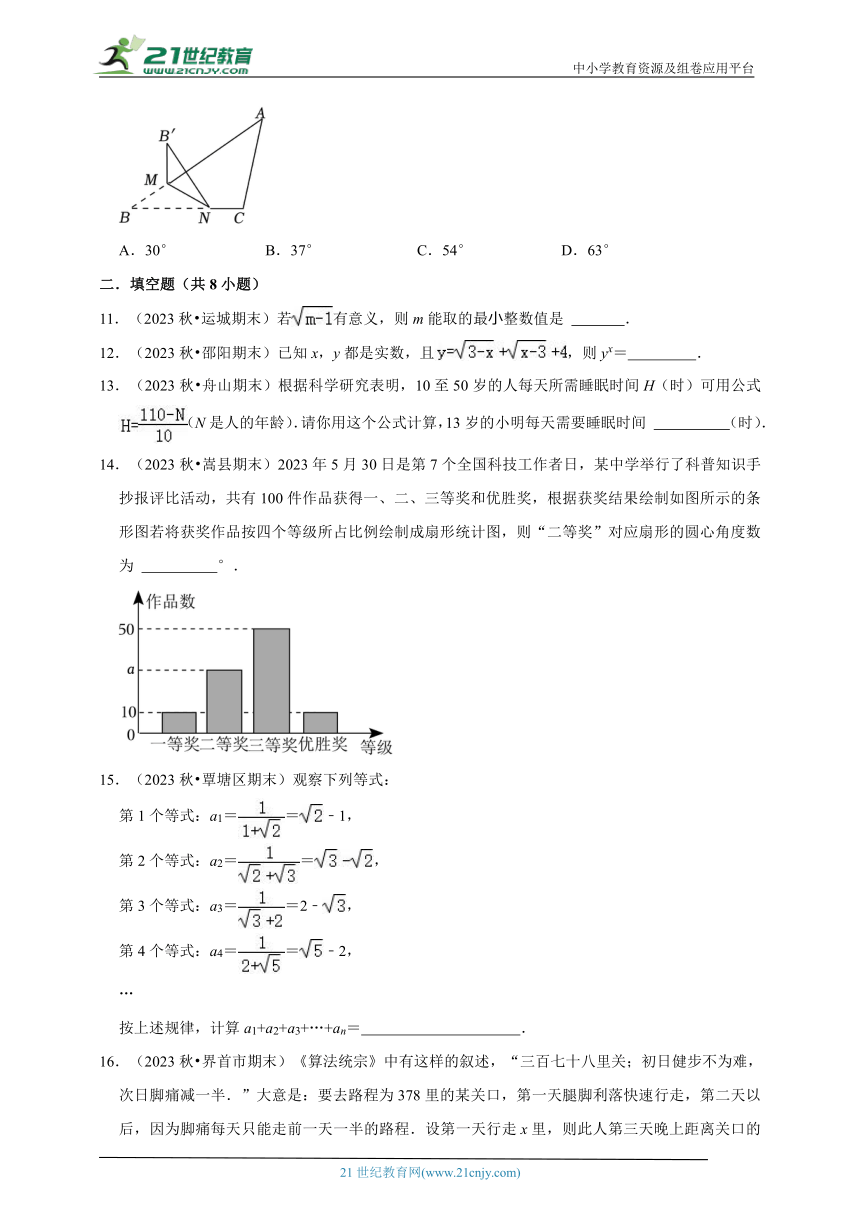
7.(2023秋 惠来县期末)如图,在△ABC中,AD平分∠BAC,则∠1、∠2、∠3的数量关系为( )
A.∠3=∠2+∠1 B.∠3=∠2+2∠1
C.∠3+∠2+∠1=180° D.∠1+∠3=2∠2
8.(2023秋 市南区期末)在学习完“垃圾分类”的相关知识后,小明和小丽一起收集了一些废电池,小明说:“我比你多收集了7节废电池啊!”小丽说:“如果你给我8节废电池,我的废电池数量就是你的2倍”.如果他们说的都是真的,设小明收集了x节废电池,小丽收集了y节废电池,则可列方程组为( )
A. B.
C. D.
9.(2023秋 肃州区校级期末)若一次函数y=(k2+1)x﹣5的图象经过点M(﹣3,y1)、N(4,y2),则y1,y2的大小关系是( )
A.y1<y2 B.y1>y2 C.y1=y2 D.无法确定
10.(2023秋 宣城期末)如图,在△ABC中,M,N分别是边AB,BC上的点,将△BMN沿MN折叠;使点B落在点B'处,若∠B=35°,∠BNM=28°,则∠AMB'的度数为( )
A.30° B.37° C.54° D.63°
二.填空题(共8小题)
11.(2023秋 运城期末)若有意义,则m能取的最 整数值是 .
12.(2023秋 邵阳期末)已知x,y都是实数,且,则yx= .
13.(2023秋 舟山期末)根据科学研究表明,10至50岁的人每天所需睡眠时间H(时)可用公式(N是人的年龄).请你用这个公式计算,13岁的小明每天需要睡眠时间 (时).
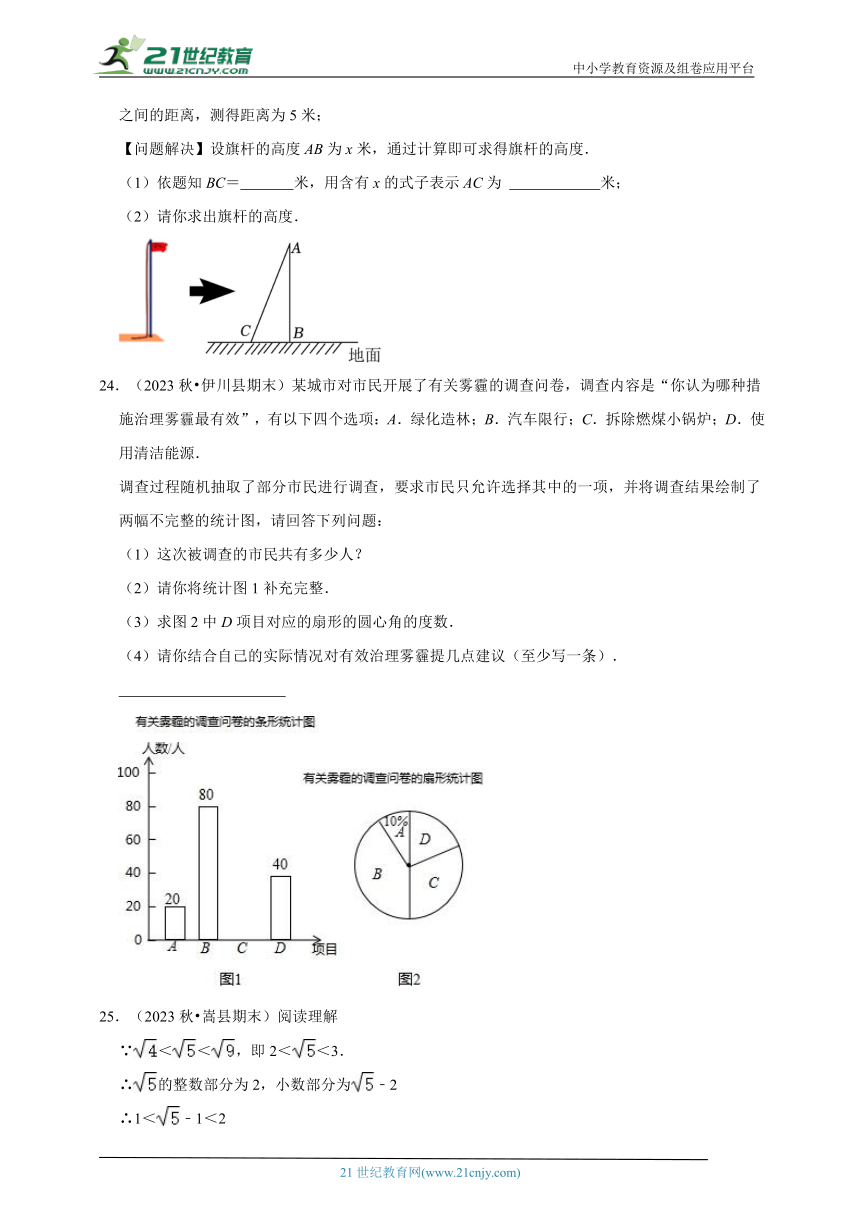
14.(2023秋 嵩县期末)2023年5月30日是第7个全国科技工作者日,某中学举行了科普知识手抄报评比活动,共有100件作品获得一、二、三等奖和优胜奖,根据获奖结果绘制如图所示的条形图若将获奖作品按四个等级所占比例绘制成扇形统计图,则“二等奖”对应扇形的圆心角度数为 °.
15.(2023秋 覃塘区期末)观察下列等式:
第1个等式:a1==﹣1,
第2个等式:a2==,
第3个等式:a3==2﹣,
第4个等式:a4==﹣2,
…
按上述规律,计算a1+a2+a3+…+an= .
16.(2023秋 界首市期末)《算法统宗》中有这样的叙述,“三百七十八里关;初日健步不为难,次日脚痛减一半.”大意是:要去路程为378里的某关口,第一天腿脚利落快速行走,第二天以后,因为脚痛每天只能走前一天一半的路程.设第一天行走x里,则此人第三天晚上距离关口的路程y(里)关于x的函数关系式为 .
17.(2023秋 市北区期末)如图a,已知长方形纸带ABCD,将纸带沿EF折叠后,点C、D分别落在H、G的位置,再沿BC折叠成图b,若∠DEF=72°,则∠GMN= °.
18.(2023秋 化州市期末)规定用符号[m]表示一个实数m的整数部分,例如:[]=0,[3.14]=3,按此规定[7﹣]的值为 .
三.解答题(共9小题)
19.(2023秋 二道区校级期末)计算:
(1);
(2).
20.(2022秋 拱墅区校级期末)已知在平面直角坐标系中,有两点P(﹣3,﹣2),点A(3,1).
(1)写出点P到x轴的距离.
(2)求出直线PA的解析式.
(3)试判断点B(a﹣3,)是否在此直线上?
21.(2023秋 淮北期末)△ABC中,∠B+∠C=2∠A,∠A:∠B=4:5,求三角形中各角的度数.
22.(2023秋 台州期末)如图,在△ABC中,∠BAC=80°,∠B=60°,AD是BC边上的高,∠ACB的平分线CF交AD于点E.求∠AEC的度数.
23.(2023秋 钢城区期末)【问题情境】某数学兴趣小组想测量学校旗杆的高度.
【实践发现】数学兴趣小组实地勘查发现:系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.
【实践探究】设计测量方案:
第一步:先测量比旗杆多出的部分绳子的长度,测得多出部分绳子的长度是1米;
第二步:把绳子向外拉直,绳子的底端恰好接触地面的点C,再测量绳子底端C与旗杆根部B点之间的距离,测得距离为5米;
【问题解决】设旗杆的高度AB为x米,通过计算即可求得旗杆的高度.
(1)依题知BC= 米,用含有x的式子表示AC为 米;
(2)请你求出旗杆的高度.
24.(2023秋 伊川县期末)某城市对市民开展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项:A.绿化造林;B.汽车限行;C.拆除燃煤小锅炉;D.使用清洁能源.
调查过程随机抽取了部分市民进行调查,要求市民只允许选择其中的一项,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的市民共有多少人?
(2)请你将统计图1补充完整.
(3)求图2中D项目对应的扇形的圆心角的度数.
(4)请你结合自己的实际情况对有效治理雾霾提几点建议(至少写一条).
25.(2023秋 嵩县期末)阅读理解
∵<<,即2<<3.
∴的整数部分为2,小数部分为﹣2
∴1<﹣1<2
∴﹣1的整数部分为1.
∴﹣1的小数部分为﹣2
解决问题:已知:a是﹣3的整数部分,b是﹣3的小数部分,
求:(1)a,b的值;
(2)(﹣a)3+(b+4)2的平方根.
26.(2023秋 麻栗坡县期末)我校将举办一年一度的秋季运动会,需要采购一批某品牌的乒乓球拍和配套的乒乓球,一副球拍标价80元,一盒球标价25元.体育商店提供了两种优惠方案,具体如下:
方案甲:买一副乒乓球拍送一盒乒乓球,其余乒乓球按原价出售;
方案乙:按购买金额打9折付款.
学校欲购买这种乒乓球拍10副,乒乓球x(x≥10)盒.
(1)请直接写出两种优惠办法实际付款金额y甲(元),y乙(元)与x(盒)之间的函数关系式.
(2)如果学校需要购买15盒乒乓球,哪种优惠方案更省钱?
(3)如果学校提供经费为1800元,选择哪个方案能购买更多乒乓球?
27.(2023秋 鹰潭期末)如图,在平面直角坐标系xOy中,直线与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长;
(2)求点C和点D的坐标;
(3)y轴上是否存在点P,使得?请说明理由.
期末重难点真题检测卷-2024-2025学年数学八年级上册北师大版
参考答案与试题解析
一.选择题(共10小题)
1.(2023秋 二道区校级期末)9的平方根是( )
A.±3 B.3 C. D.
【解答】∵(±3)2=9,
∴9的平方根是±3,
故选:A.
2.(2023秋 婺城区期末)能说明“三角形的高线一定在三角形的内部(含边界)”是假命题的反例是( )
A. B.
C. D.
【解答】解:能说明“三角形的高线一定在三角形的内部(含边界)”是假命题的反例是:
故选:C.
3.(2023秋 伊川县期末)直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )
A.121 B.120 C.90 D.不能确定
【解答】解:设另一直角边为a,斜边为a+1.
根据勾股定理可得,(a+1)2﹣a2=92.
解之得a=40.则a+1=41,则直角三角形的周长为9+40+41=90.
故选:C.
4.(2023秋 伊川县期末)如图,是某企业1~5月份利润的折线统计图,根据图中信息,下列说法错误的是( )
A.利润最高是130万
B.利润最低是100万
C.利润增长最快的是2~3月份
D.利润增长最快的是4~5月份
【解答】解:A、利润最高是130万,正确;
B、利润最低是100万,正确;
C、利润增长最快的是2~3月份,正确;
D、利润增长最快的是4~5月份,错误;
故选:D.
5.(2022秋 沈河区期末)估计的值在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
【解答】解:∵32=9,42=16,
∴估计在3和4之间.
故选:C.
6.(2024春 吐鲁番市期末)已知一次函数y=kx+2(k≠0)的函数值y随x的增大而增大,则该函数的图象大致是( )
A. B.
C. D.
【解答】解:∵一次函数y=kx+2(k≠0)的函数值y随x的增大而增大,
∴k>0,
∴此函数的图象经过一二三象限.
故选:A.
7.(2023秋 惠来县期末)如图,在△ABC中,AD平分∠BAC,则∠1、∠2、∠3的数量关系为( )
A.∠3=∠2+∠1 B.∠3=∠2+2∠1
C.∠3+∠2+∠1=180° D.∠1+∠3=2∠2
【解答】解:∵AD平分∠BAC,
∴∠DAC=∠BAD,
∴∠3=∠2+∠DAC=∠2+∠BAD,
∵∠1+∠BAD=∠2,
∴∠1+∠3=∠1+∠2+∠BAD=2∠2.
故选:D.
8.(2023秋 市南区期末)在学习完“垃圾分类”的相关知识后,小明和小丽一起收集了一些废电池,小明说:“我比你多收集了7节废电池啊!”小丽说:“如果你给我8节废电池,我的废电池数量就是你的2倍”.如果他们说的都是真的,设小明收集了x节废电池,小丽收集了y节废电池,则可列方程组为( )
A. B.
C. D.
【解答】解:由题意可得,
,
故选:B.
9.(2023秋 肃州区校级期末)若一次函数y=(k2+1)x﹣5的图象经过点M(﹣3,y1)、N(4,y2),则y1,y2的大小关系是( )
A.y1<y2 B.y1>y2 C.y1=y2 D.无法确定
【解答】解:∵在y=(k2+1)x﹣5中k2+1>0,
∴y随x的增大而增大,即y1<y2.
故选:A.
10.(2023秋 宣城期末)如图,在△ABC中,M,N分别是边AB,BC上的点,将△BMN沿MN折叠;使点B落在点B'处,若∠B=35°,∠BNM=28°,则∠AMB'的度数为( )
A.30° B.37° C.54° D.63°
【解答】解:∵△BMN沿MN折叠,使点B落在点B'处,
∴△BMN≌△B'MN,
∴∠BMN=∠B'MN,
∵∠B=35°,∠BNM=28°,
∴∠BMN=180°﹣35°﹣28°=117°,∠AMN=35°+28°=63°,
∴∠AMB'=∠B'MN﹣∠AMN=117°﹣63°=54°,
故选:C.
二.填空题(共8小题)
11.(2023秋 运城期末)若有意义,则m能取的最 整数值是 1 .
【解答】解:由题意得,m﹣1≥0,
解得,m≥1,
则m能取的最小整数值是1,
故答案为:1.
12.(2023秋 邵阳期末)已知x,y都是实数,且,则yx= 64 .
【解答】解:∵,
∴x﹣3≥0,3﹣x≥0,
∴x=3,
将x=3代入,
得:y=4,
∴yx=43=64.
故答案为:64.
13.(2023秋 舟山期末)根据科学研究表明,10至50岁的人每天所需睡眠时间H(时)可用公式(N是人的年龄).请你用这个公式计算,13岁的小明每天需要睡眠时间 9.7 (时).
【解答】解:当N=13时,
故答案为:9.7.
14.(2023秋 嵩县期末)2023年5月30日是第7个全国科技工作者日,某中学举行了科普知识手抄报评比活动,共有100件作品获得一、二、三等奖和优胜奖,根据获奖结果绘制如图所示的条形图若将获奖作品按四个等级所占比例绘制成扇形统计图,则“二等奖”对应扇形的圆心角度数为 108 °.
【解答】解:由条形统计图可得,
a=100﹣10﹣50﹣10=30,
“一等奖”对应扇形的圆心角度数为:360°×=108°,
故答案为:108.
15.(2023秋 覃塘区期末)观察下列等式:
第1个等式:a1==﹣1,
第2个等式:a2==,
第3个等式:a3==2﹣,
第4个等式:a4==﹣2,
…
按上述规律,计算a1+a2+a3+…+an= ﹣1 .
【解答】解:第1个等式:a1==﹣1,
第2个等式:a2==,
第3个等式:a3==2﹣,
第4个等式:a4==﹣2,
…
a1+a2+a3+…+an
=﹣1+﹣+…+﹣
=﹣1
故答案为:﹣1.
16.(2023秋 界首市期末)《算法统宗》中有这样的叙述,“三百七十八里关;初日健步不为难,次日脚痛减一半.”大意是:要去路程为378里的某关口,第一天腿脚利落快速行走,第二天以后,因为脚痛每天只能走前一天一半的路程.设第一天行走x里,则此人第三天晚上距离关口的路程y(里)关于x的函数关系式为 y=﹣x+378 .
【解答】解:设第一天行走x里,则第二天行走里,第三天行走×x=x里,
根据题意得:y=378﹣x﹣x﹣x=378﹣x,
故答案为:y=﹣x+378.
17.(2023秋 市北区期末)如图a,已知长方形纸带ABCD,将纸带沿EF折叠后,点C、D分别落在H、G的位置,再沿BC折叠成图b,若∠DEF=72°,则∠GMN= 72 °.
【解答】解:∵AD∥CB,
∴∠EFC+∠DEF=180°,∠EFB=∠DEF,
即∠EFC=180°﹣72°=108°,∠EFB=72°,
∴∠BFH=108°﹣72°=36°.
∵∠H=∠D=90°,
∴∠HMF=180°﹣90°﹣36°=54°.
由折叠可得:∠NMF=∠HMF=54°,
∴∠GMN=72°.
故答案为:72.
18.(2023秋 化州市期末)规定用符号[m]表示一个实数m的整数部分,例如:[]=0,[3.14]=3,按此规定[7﹣]的值为 4 .
【解答】解:∵2<<3,
∴[7﹣]=4.
故答案为:4.
三.解答题(共9小题)
19.(2023秋 二道区校级期末)计算:
(1);
(2).
【解答】解:(1)
=3﹣2+3
=+3;
(2)
=﹣
=﹣
=﹣4.
20.(2022秋 拱墅区校级期末)已知在平面直角坐标系中,有两点P(﹣3,﹣2),点A(3,1).
(1)写出点P到x轴的距离.
(2)求出直线PA的解析式.
(3)试判断点B(a﹣3,)是否在此直线上?
【解答】解:(1)∵P点坐标为(﹣3,﹣2),
∴点P到x轴的距离为2;
(2)设直线PA的解析式为y=kx+b,
把P(﹣3,﹣2)、A(3,1)分别代入得,
解得,
∴直线AP的解析式为y=x﹣;
(3)当x=a﹣3时,y=(a﹣3)﹣=a﹣2,
若a﹣2=a,
解得a=﹣12,
当a=﹣12时,点B(a﹣3,)在此直线上;当a≠﹣12时,点B(a﹣3,)不在此直线上.
21.(2023秋 淮北期末)△ABC中,∠B+∠C=2∠A,∠A:∠B=4:5,求三角形中各角的度数.
【解答】解:设∠A=4x,∠B=5x,
则∠C=180°﹣4x﹣5x=180°﹣9x,
∵∠B+∠C=2∠A,
∴5x+180°﹣9x=2×4x,
解得x=15°,
∴∠A=4×15°=60°,∠B=5×15°=75°,∠C=180°﹣60°﹣75°=45°,
综上所述,三角形中各角的度数为∠A=60°,∠B=75°,∠C=45°.
22.(2023秋 台州期末)如图,在△ABC中,∠BAC=80°,∠B=60°,AD是BC边上的高,∠ACB的平分线CF交AD于点E.求∠AEC的度数.
【解答】解:∵在△ABC中,∠BAC=80°,∠B=60°,
∴∠ACB=180°﹣∠CAB﹣∠B=180°﹣80°﹣60°=40°,
又∵CF是∠ACB的平分线,
∴,
又∵AD是BC边上的高,
∴∠ADC=90°,
∴∠AEC=90°+∠ECD=90°+20°=110°.
23.(2023秋 钢城区期末)【问题情境】某数学兴趣小组想测量学校旗杆的高度.
【实践发现】数学兴趣小组实地勘查发现:系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.
【实践探究】设计测量方案:
第一步:先测量比旗杆多出的部分绳子的长度,测得多出部分绳子的长度是1米;
第二步:把绳子向外拉直,绳子的底端恰好接触地面的点C,再测量绳子底端C与旗杆根部B点之间的距离,测得距离为5米;
【问题解决】设旗杆的高度AB为x米,通过计算即可求得旗杆的高度.
(1)依题知BC= 5 米,用含有x的式子表示AC为 (x+1) 米;
(2)请你求出旗杆的高度.
【解答】解:(1)根据题意知:BC=5米,AC=(x+1)米.
故答案为:5;(x+1);
(2)在直角△ABC中,由勾股定理得:
BC2+AB2=AC2,
即52+x2=(x+1)2.
解得x=12.
答:旗杆的高度为12米.
24.(2023秋 伊川县期末)某城市对市民开展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项:A.绿化造林;B.汽车限行;C.拆除燃煤小锅炉;D.使用清洁能源.
调查过程随机抽取了部分市民进行调查,要求市民只允许选择其中的一项,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的市民共有多少人?
(2)请你将统计图1补充完整.
(3)求图2中D项目对应的扇形的圆心角的度数.
(4)请你结合自己的实际情况对有效治理雾霾提几点建议(至少写一条).
①建议绿色出行,尽量乘坐公共交通工具上班,减少开车的次数,
②加强植树造林,增加绿化面积,提高绿化率,还绿水青山.
【解答】解:(1)20÷10%=200(人),
答:本次调查的人数为200人;
(2)C项目的人数有:200﹣20﹣80﹣40=60(人),补全条形统计图如图所示:
(3)360°×=72°,
答:图2中D项目对应的扇形的圆心角的度数为72°;
(4)①建议绿色出行,尽量乘坐公共交通工具上班,减少开车的次数,
②加强植树造林,增加绿化面积,提高绿化率,还绿水青山.
故答案为:①建议绿色出行,尽量乘坐公共交通工具上班,减少开车的次数,
②加强植树造林,增加绿化面积,提高绿化率,还绿水青山.
25.(2023秋 嵩县期末)阅读理解
∵<<,即2<<3.
∴的整数部分为2,小数部分为﹣2
∴1<﹣1<2
∴﹣1的整数部分为1.
∴﹣1的小数部分为﹣2
解决问题:已知:a是﹣3的整数部分,b是﹣3的小数部分,
求:(1)a,b的值;
(2)(﹣a)3+(b+4)2的平方根.
【解答】解:(1)∵<<,
∴4<<5,
∴1<﹣3<2,
∴a=1,b=﹣4,
(2)(﹣a)3+(b+4)2
=(﹣1)3+(﹣4+4)2
=﹣1+17
=16,
故(﹣a)3+(b+4)2的平方根是:±4.
26.(2023秋 麻栗坡县期末)我校将举办一年一度的秋季运动会,需要采购一批某品牌的乒乓球拍和配套的乒乓球,一副球拍标价80元,一盒球标价25元.体育商店提供了两种优惠方案,具体如下:
方案甲:买一副乒乓球拍送一盒乒乓球,其余乒乓球按原价出售;
方案乙:按购买金额打9折付款.
学校欲购买这种乒乓球拍10副,乒乓球x(x≥10)盒.
(1)请直接写出两种优惠办法实际付款金额y甲(元),y乙(元)与x(盒)之间的函数关系式.
(2)如果学校需要购买15盒乒乓球,哪种优惠方案更省钱?
(3)如果学校提供经费为1800元,选择哪个方案能购买更多乒乓球?
【解答】解:(1)由题意得:
y甲=10×80+25(x﹣10)=25x+550,
y乙=25×0.9x+80×0.9×10=22.5x+720,
(2)根据(1)中解析式,y甲=25x+550,y乙=22.5x+720,
当x=15时y甲=25×15+550=925(元),
y乙=22.5×15+720=1057.5(元),
∵925<1057.5,
∴方案甲更省钱;
(3)根据(1)中解析式,y甲=25x+550,y乙=22.5x+720,
当y甲=1800元时,1800=25x+550,解得:x=50,
当y乙=1800元时,1800=22.5x+720,解得:x=48,
∵50>48,
∴学校提供经费为1800元,选择方案甲能购买更多乒乓球.
27.(2023秋 鹰潭期末)如图,在平面直角坐标系xOy中,直线与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长;
(2)求点C和点D的坐标;
(3)y轴上是否存在点P,使得?请说明理由.
【解答】解:(1)令x=0得:y=4,
∴B(0,4).
∴OB=4,
令y=0得:,
解得:x=3,
∴A(3,0).
∴OA=3.
在Rt△OAB中,.
故AB的长为5.
(2)∵AC=AB=5,
∴OC=OA+AC=3+5=8,
∴C(8,0).
设OD=x,则CD=DB=x+4.
在Rt△OCD中,DC2=OD2+OC2,即(x+4)2=x2+82,
解得:x=6,
∴D(0,﹣6).
故C为(8,0),D为(0,﹣6).
(3)存在,理由如下:
∵,
∴.
∵点P在y轴上,S△PAB=12,
∴BP OA=12,即×3BP=12,
解得:BP=8,
∴P点的坐标为(0,12)或(0,﹣4).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末重难点真题检测卷-2024-2025学年数学八年级上册北师大版
一.选择题(共10小题)
1.(2023秋 二道区校级期末)9的平方根是( )
A.±3 B.3 C. D.
2.(2023秋 婺城区期末)能说明“三角形的高线一定在三角形的内部(含边界)”是假命题的反例是( )
A. B.
C. D.
3.(2023秋 伊川县期末)直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )
A.121 B.120 C.90 D.不能确定
4.(2023秋 伊川县期末)如图,是某企业1~5月份利润的折线统计图,根据图中信息,下列说法错误的是( )
A.利润最高是130万
B.利润最低是100万
C.利润增长最快的是2~3月份
D.利润增长最快的是4~5月份
5.(2022秋 沈河区期末)估计的值在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
6.(2024春 吐鲁番市期末)已知一次函数y=kx+2(k≠0)的函数值y随x的增大而增大,则该函数的图象大致是( )
A. B.
C. D.
7.(2023秋 惠来县期末)如图,在△ABC中,AD平分∠BAC,则∠1、∠2、∠3的数量关系为( )
A.∠3=∠2+∠1 B.∠3=∠2+2∠1
C.∠3+∠2+∠1=180° D.∠1+∠3=2∠2
8.(2023秋 市南区期末)在学习完“垃圾分类”的相关知识后,小明和小丽一起收集了一些废电池,小明说:“我比你多收集了7节废电池啊!”小丽说:“如果你给我8节废电池,我的废电池数量就是你的2倍”.如果他们说的都是真的,设小明收集了x节废电池,小丽收集了y节废电池,则可列方程组为( )
A. B.
C. D.
9.(2023秋 肃州区校级期末)若一次函数y=(k2+1)x﹣5的图象经过点M(﹣3,y1)、N(4,y2),则y1,y2的大小关系是( )
A.y1<y2 B.y1>y2 C.y1=y2 D.无法确定
10.(2023秋 宣城期末)如图,在△ABC中,M,N分别是边AB,BC上的点,将△BMN沿MN折叠;使点B落在点B'处,若∠B=35°,∠BNM=28°,则∠AMB'的度数为( )
A.30° B.37° C.54° D.63°
二.填空题(共8小题)
11.(2023秋 运城期末)若有意义,则m能取的最 整数值是 .
12.(2023秋 邵阳期末)已知x,y都是实数,且,则yx= .
13.(2023秋 舟山期末)根据科学研究表明,10至50岁的人每天所需睡眠时间H(时)可用公式(N是人的年龄).请你用这个公式计算,13岁的小明每天需要睡眠时间 (时).
14.(2023秋 嵩县期末)2023年5月30日是第7个全国科技工作者日,某中学举行了科普知识手抄报评比活动,共有100件作品获得一、二、三等奖和优胜奖,根据获奖结果绘制如图所示的条形图若将获奖作品按四个等级所占比例绘制成扇形统计图,则“二等奖”对应扇形的圆心角度数为 °.
15.(2023秋 覃塘区期末)观察下列等式:
第1个等式:a1==﹣1,
第2个等式:a2==,
第3个等式:a3==2﹣,
第4个等式:a4==﹣2,
…
按上述规律,计算a1+a2+a3+…+an= .
16.(2023秋 界首市期末)《算法统宗》中有这样的叙述,“三百七十八里关;初日健步不为难,次日脚痛减一半.”大意是:要去路程为378里的某关口,第一天腿脚利落快速行走,第二天以后,因为脚痛每天只能走前一天一半的路程.设第一天行走x里,则此人第三天晚上距离关口的路程y(里)关于x的函数关系式为 .
17.(2023秋 市北区期末)如图a,已知长方形纸带ABCD,将纸带沿EF折叠后,点C、D分别落在H、G的位置,再沿BC折叠成图b,若∠DEF=72°,则∠GMN= °.
18.(2023秋 化州市期末)规定用符号[m]表示一个实数m的整数部分,例如:[]=0,[3.14]=3,按此规定[7﹣]的值为 .
三.解答题(共9小题)
19.(2023秋 二道区校级期末)计算:
(1);
(2).
20.(2022秋 拱墅区校级期末)已知在平面直角坐标系中,有两点P(﹣3,﹣2),点A(3,1).
(1)写出点P到x轴的距离.
(2)求出直线PA的解析式.
(3)试判断点B(a﹣3,)是否在此直线上?
21.(2023秋 淮北期末)△ABC中,∠B+∠C=2∠A,∠A:∠B=4:5,求三角形中各角的度数.
22.(2023秋 台州期末)如图,在△ABC中,∠BAC=80°,∠B=60°,AD是BC边上的高,∠ACB的平分线CF交AD于点E.求∠AEC的度数.
23.(2023秋 钢城区期末)【问题情境】某数学兴趣小组想测量学校旗杆的高度.
【实践发现】数学兴趣小组实地勘查发现:系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.
【实践探究】设计测量方案:
第一步:先测量比旗杆多出的部分绳子的长度,测得多出部分绳子的长度是1米;
第二步:把绳子向外拉直,绳子的底端恰好接触地面的点C,再测量绳子底端C与旗杆根部B点之间的距离,测得距离为5米;
【问题解决】设旗杆的高度AB为x米,通过计算即可求得旗杆的高度.
(1)依题知BC= 米,用含有x的式子表示AC为 米;
(2)请你求出旗杆的高度.
24.(2023秋 伊川县期末)某城市对市民开展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项:A.绿化造林;B.汽车限行;C.拆除燃煤小锅炉;D.使用清洁能源.
调查过程随机抽取了部分市民进行调查,要求市民只允许选择其中的一项,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的市民共有多少人?
(2)请你将统计图1补充完整.
(3)求图2中D项目对应的扇形的圆心角的度数.
(4)请你结合自己的实际情况对有效治理雾霾提几点建议(至少写一条).
25.(2023秋 嵩县期末)阅读理解
∵<<,即2<<3.
∴的整数部分为2,小数部分为﹣2
∴1<﹣1<2
∴﹣1的整数部分为1.
∴﹣1的小数部分为﹣2
解决问题:已知:a是﹣3的整数部分,b是﹣3的小数部分,
求:(1)a,b的值;
(2)(﹣a)3+(b+4)2的平方根.
26.(2023秋 麻栗坡县期末)我校将举办一年一度的秋季运动会,需要采购一批某品牌的乒乓球拍和配套的乒乓球,一副球拍标价80元,一盒球标价25元.体育商店提供了两种优惠方案,具体如下:
方案甲:买一副乒乓球拍送一盒乒乓球,其余乒乓球按原价出售;
方案乙:按购买金额打9折付款.
学校欲购买这种乒乓球拍10副,乒乓球x(x≥10)盒.
(1)请直接写出两种优惠办法实际付款金额y甲(元),y乙(元)与x(盒)之间的函数关系式.
(2)如果学校需要购买15盒乒乓球,哪种优惠方案更省钱?
(3)如果学校提供经费为1800元,选择哪个方案能购买更多乒乓球?
27.(2023秋 鹰潭期末)如图,在平面直角坐标系xOy中,直线与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长;
(2)求点C和点D的坐标;
(3)y轴上是否存在点P,使得?请说明理由.
期末重难点真题检测卷-2024-2025学年数学八年级上册北师大版
参考答案与试题解析
一.选择题(共10小题)
1.(2023秋 二道区校级期末)9的平方根是( )
A.±3 B.3 C. D.
【解答】∵(±3)2=9,
∴9的平方根是±3,
故选:A.
2.(2023秋 婺城区期末)能说明“三角形的高线一定在三角形的内部(含边界)”是假命题的反例是( )
A. B.
C. D.
【解答】解:能说明“三角形的高线一定在三角形的内部(含边界)”是假命题的反例是:
故选:C.
3.(2023秋 伊川县期末)直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )
A.121 B.120 C.90 D.不能确定
【解答】解:设另一直角边为a,斜边为a+1.
根据勾股定理可得,(a+1)2﹣a2=92.
解之得a=40.则a+1=41,则直角三角形的周长为9+40+41=90.
故选:C.
4.(2023秋 伊川县期末)如图,是某企业1~5月份利润的折线统计图,根据图中信息,下列说法错误的是( )
A.利润最高是130万
B.利润最低是100万
C.利润增长最快的是2~3月份
D.利润增长最快的是4~5月份
【解答】解:A、利润最高是130万,正确;
B、利润最低是100万,正确;
C、利润增长最快的是2~3月份,正确;
D、利润增长最快的是4~5月份,错误;
故选:D.
5.(2022秋 沈河区期末)估计的值在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
【解答】解:∵32=9,42=16,
∴估计在3和4之间.
故选:C.
6.(2024春 吐鲁番市期末)已知一次函数y=kx+2(k≠0)的函数值y随x的增大而增大,则该函数的图象大致是( )
A. B.
C. D.
【解答】解:∵一次函数y=kx+2(k≠0)的函数值y随x的增大而增大,
∴k>0,
∴此函数的图象经过一二三象限.
故选:A.
7.(2023秋 惠来县期末)如图,在△ABC中,AD平分∠BAC,则∠1、∠2、∠3的数量关系为( )
A.∠3=∠2+∠1 B.∠3=∠2+2∠1
C.∠3+∠2+∠1=180° D.∠1+∠3=2∠2
【解答】解:∵AD平分∠BAC,
∴∠DAC=∠BAD,
∴∠3=∠2+∠DAC=∠2+∠BAD,
∵∠1+∠BAD=∠2,
∴∠1+∠3=∠1+∠2+∠BAD=2∠2.
故选:D.
8.(2023秋 市南区期末)在学习完“垃圾分类”的相关知识后,小明和小丽一起收集了一些废电池,小明说:“我比你多收集了7节废电池啊!”小丽说:“如果你给我8节废电池,我的废电池数量就是你的2倍”.如果他们说的都是真的,设小明收集了x节废电池,小丽收集了y节废电池,则可列方程组为( )
A. B.
C. D.
【解答】解:由题意可得,
,
故选:B.
9.(2023秋 肃州区校级期末)若一次函数y=(k2+1)x﹣5的图象经过点M(﹣3,y1)、N(4,y2),则y1,y2的大小关系是( )
A.y1<y2 B.y1>y2 C.y1=y2 D.无法确定
【解答】解:∵在y=(k2+1)x﹣5中k2+1>0,
∴y随x的增大而增大,即y1<y2.
故选:A.
10.(2023秋 宣城期末)如图,在△ABC中,M,N分别是边AB,BC上的点,将△BMN沿MN折叠;使点B落在点B'处,若∠B=35°,∠BNM=28°,则∠AMB'的度数为( )
A.30° B.37° C.54° D.63°
【解答】解:∵△BMN沿MN折叠,使点B落在点B'处,
∴△BMN≌△B'MN,
∴∠BMN=∠B'MN,
∵∠B=35°,∠BNM=28°,
∴∠BMN=180°﹣35°﹣28°=117°,∠AMN=35°+28°=63°,
∴∠AMB'=∠B'MN﹣∠AMN=117°﹣63°=54°,
故选:C.
二.填空题(共8小题)
11.(2023秋 运城期末)若有意义,则m能取的最 整数值是 1 .
【解答】解:由题意得,m﹣1≥0,
解得,m≥1,
则m能取的最小整数值是1,
故答案为:1.
12.(2023秋 邵阳期末)已知x,y都是实数,且,则yx= 64 .
【解答】解:∵,
∴x﹣3≥0,3﹣x≥0,
∴x=3,
将x=3代入,
得:y=4,
∴yx=43=64.
故答案为:64.
13.(2023秋 舟山期末)根据科学研究表明,10至50岁的人每天所需睡眠时间H(时)可用公式(N是人的年龄).请你用这个公式计算,13岁的小明每天需要睡眠时间 9.7 (时).
【解答】解:当N=13时,
故答案为:9.7.
14.(2023秋 嵩县期末)2023年5月30日是第7个全国科技工作者日,某中学举行了科普知识手抄报评比活动,共有100件作品获得一、二、三等奖和优胜奖,根据获奖结果绘制如图所示的条形图若将获奖作品按四个等级所占比例绘制成扇形统计图,则“二等奖”对应扇形的圆心角度数为 108 °.
【解答】解:由条形统计图可得,
a=100﹣10﹣50﹣10=30,
“一等奖”对应扇形的圆心角度数为:360°×=108°,
故答案为:108.
15.(2023秋 覃塘区期末)观察下列等式:
第1个等式:a1==﹣1,
第2个等式:a2==,
第3个等式:a3==2﹣,
第4个等式:a4==﹣2,
…
按上述规律,计算a1+a2+a3+…+an= ﹣1 .
【解答】解:第1个等式:a1==﹣1,
第2个等式:a2==,
第3个等式:a3==2﹣,
第4个等式:a4==﹣2,
…
a1+a2+a3+…+an
=﹣1+﹣+…+﹣
=﹣1
故答案为:﹣1.
16.(2023秋 界首市期末)《算法统宗》中有这样的叙述,“三百七十八里关;初日健步不为难,次日脚痛减一半.”大意是:要去路程为378里的某关口,第一天腿脚利落快速行走,第二天以后,因为脚痛每天只能走前一天一半的路程.设第一天行走x里,则此人第三天晚上距离关口的路程y(里)关于x的函数关系式为 y=﹣x+378 .
【解答】解:设第一天行走x里,则第二天行走里,第三天行走×x=x里,
根据题意得:y=378﹣x﹣x﹣x=378﹣x,
故答案为:y=﹣x+378.
17.(2023秋 市北区期末)如图a,已知长方形纸带ABCD,将纸带沿EF折叠后,点C、D分别落在H、G的位置,再沿BC折叠成图b,若∠DEF=72°,则∠GMN= 72 °.
【解答】解:∵AD∥CB,
∴∠EFC+∠DEF=180°,∠EFB=∠DEF,
即∠EFC=180°﹣72°=108°,∠EFB=72°,
∴∠BFH=108°﹣72°=36°.
∵∠H=∠D=90°,
∴∠HMF=180°﹣90°﹣36°=54°.
由折叠可得:∠NMF=∠HMF=54°,
∴∠GMN=72°.
故答案为:72.
18.(2023秋 化州市期末)规定用符号[m]表示一个实数m的整数部分,例如:[]=0,[3.14]=3,按此规定[7﹣]的值为 4 .
【解答】解:∵2<<3,
∴[7﹣]=4.
故答案为:4.
三.解答题(共9小题)
19.(2023秋 二道区校级期末)计算:
(1);
(2).
【解答】解:(1)
=3﹣2+3
=+3;
(2)
=﹣
=﹣
=﹣4.
20.(2022秋 拱墅区校级期末)已知在平面直角坐标系中,有两点P(﹣3,﹣2),点A(3,1).
(1)写出点P到x轴的距离.
(2)求出直线PA的解析式.
(3)试判断点B(a﹣3,)是否在此直线上?
【解答】解:(1)∵P点坐标为(﹣3,﹣2),
∴点P到x轴的距离为2;
(2)设直线PA的解析式为y=kx+b,
把P(﹣3,﹣2)、A(3,1)分别代入得,
解得,
∴直线AP的解析式为y=x﹣;
(3)当x=a﹣3时,y=(a﹣3)﹣=a﹣2,
若a﹣2=a,
解得a=﹣12,
当a=﹣12时,点B(a﹣3,)在此直线上;当a≠﹣12时,点B(a﹣3,)不在此直线上.
21.(2023秋 淮北期末)△ABC中,∠B+∠C=2∠A,∠A:∠B=4:5,求三角形中各角的度数.
【解答】解:设∠A=4x,∠B=5x,
则∠C=180°﹣4x﹣5x=180°﹣9x,
∵∠B+∠C=2∠A,
∴5x+180°﹣9x=2×4x,
解得x=15°,
∴∠A=4×15°=60°,∠B=5×15°=75°,∠C=180°﹣60°﹣75°=45°,
综上所述,三角形中各角的度数为∠A=60°,∠B=75°,∠C=45°.
22.(2023秋 台州期末)如图,在△ABC中,∠BAC=80°,∠B=60°,AD是BC边上的高,∠ACB的平分线CF交AD于点E.求∠AEC的度数.
【解答】解:∵在△ABC中,∠BAC=80°,∠B=60°,
∴∠ACB=180°﹣∠CAB﹣∠B=180°﹣80°﹣60°=40°,
又∵CF是∠ACB的平分线,
∴,
又∵AD是BC边上的高,
∴∠ADC=90°,
∴∠AEC=90°+∠ECD=90°+20°=110°.
23.(2023秋 钢城区期末)【问题情境】某数学兴趣小组想测量学校旗杆的高度.
【实践发现】数学兴趣小组实地勘查发现:系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.
【实践探究】设计测量方案:
第一步:先测量比旗杆多出的部分绳子的长度,测得多出部分绳子的长度是1米;
第二步:把绳子向外拉直,绳子的底端恰好接触地面的点C,再测量绳子底端C与旗杆根部B点之间的距离,测得距离为5米;
【问题解决】设旗杆的高度AB为x米,通过计算即可求得旗杆的高度.
(1)依题知BC= 5 米,用含有x的式子表示AC为 (x+1) 米;
(2)请你求出旗杆的高度.
【解答】解:(1)根据题意知:BC=5米,AC=(x+1)米.
故答案为:5;(x+1);
(2)在直角△ABC中,由勾股定理得:
BC2+AB2=AC2,
即52+x2=(x+1)2.
解得x=12.
答:旗杆的高度为12米.
24.(2023秋 伊川县期末)某城市对市民开展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项:A.绿化造林;B.汽车限行;C.拆除燃煤小锅炉;D.使用清洁能源.
调查过程随机抽取了部分市民进行调查,要求市民只允许选择其中的一项,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的市民共有多少人?
(2)请你将统计图1补充完整.
(3)求图2中D项目对应的扇形的圆心角的度数.
(4)请你结合自己的实际情况对有效治理雾霾提几点建议(至少写一条).
①建议绿色出行,尽量乘坐公共交通工具上班,减少开车的次数,
②加强植树造林,增加绿化面积,提高绿化率,还绿水青山.
【解答】解:(1)20÷10%=200(人),
答:本次调查的人数为200人;
(2)C项目的人数有:200﹣20﹣80﹣40=60(人),补全条形统计图如图所示:
(3)360°×=72°,
答:图2中D项目对应的扇形的圆心角的度数为72°;
(4)①建议绿色出行,尽量乘坐公共交通工具上班,减少开车的次数,
②加强植树造林,增加绿化面积,提高绿化率,还绿水青山.
故答案为:①建议绿色出行,尽量乘坐公共交通工具上班,减少开车的次数,
②加强植树造林,增加绿化面积,提高绿化率,还绿水青山.
25.(2023秋 嵩县期末)阅读理解
∵<<,即2<<3.
∴的整数部分为2,小数部分为﹣2
∴1<﹣1<2
∴﹣1的整数部分为1.
∴﹣1的小数部分为﹣2
解决问题:已知:a是﹣3的整数部分,b是﹣3的小数部分,
求:(1)a,b的值;
(2)(﹣a)3+(b+4)2的平方根.
【解答】解:(1)∵<<,
∴4<<5,
∴1<﹣3<2,
∴a=1,b=﹣4,
(2)(﹣a)3+(b+4)2
=(﹣1)3+(﹣4+4)2
=﹣1+17
=16,
故(﹣a)3+(b+4)2的平方根是:±4.
26.(2023秋 麻栗坡县期末)我校将举办一年一度的秋季运动会,需要采购一批某品牌的乒乓球拍和配套的乒乓球,一副球拍标价80元,一盒球标价25元.体育商店提供了两种优惠方案,具体如下:
方案甲:买一副乒乓球拍送一盒乒乓球,其余乒乓球按原价出售;
方案乙:按购买金额打9折付款.
学校欲购买这种乒乓球拍10副,乒乓球x(x≥10)盒.
(1)请直接写出两种优惠办法实际付款金额y甲(元),y乙(元)与x(盒)之间的函数关系式.
(2)如果学校需要购买15盒乒乓球,哪种优惠方案更省钱?
(3)如果学校提供经费为1800元,选择哪个方案能购买更多乒乓球?
【解答】解:(1)由题意得:
y甲=10×80+25(x﹣10)=25x+550,
y乙=25×0.9x+80×0.9×10=22.5x+720,
(2)根据(1)中解析式,y甲=25x+550,y乙=22.5x+720,
当x=15时y甲=25×15+550=925(元),
y乙=22.5×15+720=1057.5(元),
∵925<1057.5,
∴方案甲更省钱;
(3)根据(1)中解析式,y甲=25x+550,y乙=22.5x+720,
当y甲=1800元时,1800=25x+550,解得:x=50,
当y乙=1800元时,1800=22.5x+720,解得:x=48,
∵50>48,
∴学校提供经费为1800元,选择方案甲能购买更多乒乓球.
27.(2023秋 鹰潭期末)如图,在平面直角坐标系xOy中,直线与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长;
(2)求点C和点D的坐标;
(3)y轴上是否存在点P,使得?请说明理由.
【解答】解:(1)令x=0得:y=4,
∴B(0,4).
∴OB=4,
令y=0得:,
解得:x=3,
∴A(3,0).
∴OA=3.
在Rt△OAB中,.
故AB的长为5.
(2)∵AC=AB=5,
∴OC=OA+AC=3+5=8,
∴C(8,0).
设OD=x,则CD=DB=x+4.
在Rt△OCD中,DC2=OD2+OC2,即(x+4)2=x2+82,
解得:x=6,
∴D(0,﹣6).
故C为(8,0),D为(0,﹣6).
(3)存在,理由如下:
∵,
∴.
∵点P在y轴上,S△PAB=12,
∴BP OA=12,即×3BP=12,
解得:BP=8,
∴P点的坐标为(0,12)或(0,﹣4).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
