人教版 2024-2025学年数学八年级上册期末真题重组卷(含解析)
文档属性
| 名称 | 人教版 2024-2025学年数学八年级上册期末真题重组卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 616.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 08:48:11 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末真题重组卷-2024-2025学年数学八年级上册人教版
一.选择题(共10小题)
1.(2023秋 南充期末)体育是一个锻炼身体,增强体质,培养道德和意志品质的教育过程,是培养全面发展的人的一个重要方面,下列体育图标是轴对称图形的是( )
A. B.
C. D.
2.(2024春 晋江市期末)空调安装在墙上时,一般都会采用如图的方法固定,这种方法应用的几何原理是( )
A.两点确定一条直线 B.两点之间线段最短
C.三角形的稳定性 D.垂线段最短
3.(2023秋 汕尾期末)如果将一副三角板按如图的方式叠放,则∠1的度数为( )
A.105° B.120° C.75° D.45°
4.(2023秋 赣县区期末)点(﹣2,3)关于x轴的对称点的坐标为( )
A.(﹣2,﹣3) B.(2,3) C.(﹣2,3) D.(2,﹣3)
5.(2023秋 德庆县期末)如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )
A.6米 B.9米 C.12米 D.15米
6.(2023秋 高邮市期末)如图,已知三角形卡纸的三边长分别为6cm、8cm、10cm,要将这张卡纸剪成两个三角形,且其中必须有一个三角形是等腰三角形,在用不同剪法剪得的这些等腰三角形中,腰长的最小值为( )
A. B.5cm C. D.6cm
7.(2023秋 双辽市期末)如图,在△ABC中,AC=18cm,BC=20cm,点M从点A出发以每秒2cm的速度向点C运动,点N从点C出发以每秒1.6cm的速度向点B运动,其中一个动点到达终点时,另一个动点也随之停止运动,当△CMN是以MN为底的等腰三角形时,则这时等腰三角形的腰长是( )
A.5cm B.6cm C.7cm D.8cm
8.(2017秋 嘉兴期末)用尺规作图作∠BAC的平分线AD,痕迹如图所示,则此作图的依据是( )
A.SAS B.SSS C.ASA D.AAS
9.(2023秋 香洲区期末)如图,在等边△ABC中,E为AB上一点,过点E的直线交AC于点F,交BC延长线于点D,作EG⊥AC垂足为G,如 AE=CD,AB=α,则GF的长为( )
A. B. C. D.
10.(2023秋 荣昌区校级期末)若关于x的一元一次不等式组无解,且关于y的分式方程有非负整数解,则符合条件的所有整数a的和为( )
A.7 B.8 C.14 D.15
二.填空题(共8小题)
11.(2023秋 固始县期末)如图,将四边形ABCD去掉一个70°的角得到一个五边形BCDEF,则∠1+∠2= °.
12.(2023秋 浉河区期末)如图,B、E、C、F四点在同一直线上,且BE=CF,AC=DF,添加一个条件 ,使△ABC≌△DEF(写出一个即可).
13.(2023春 武功县期末)如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=5,若点Q是射线OB上一点,OQ=4,则△ODQ的面积是 .
14.(2023秋 福田区校级期末)已知P1(a﹣1,5)和P2(2,b﹣1)关于x轴对称,则(a+b)2024的值为 .
15.(2024春 滕州市期末)如图,△ABC中,AB=AC=13,BC=10,AD是BC边上的中线且AD=12,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为 .
16.(2024春 冷水滩区期末)若x2+2(m﹣3)x+16是完全平方式,则m的值等于 .
17.(2024春 太平区期末)已知关于x的分式方程﹣2=的解是非负数,则m的取值范围是 .
18.(2023秋 西城区期末)甲、乙两名同学作为志愿者帮助图书馆清点一批图书,甲3h清点完这批图书的,乙加入清点剩余的图书,两人合作2.4h清点完剩余的图书.如果乙单独清点这批图书需要几小时?若设乙单独清点这批图书需要xh,则根据题意可列方程为 .
三.解答题(共9小题)
19.(2023秋 门头沟区期末)解分式方程:.
20.(2022秋 顺庆区校级期末)先化简代数式,再从2,﹣2,1,﹣1四个数中选择一个你喜欢的数代入求值.
21.(2023秋 重庆期末)因式分解:
(1)8a2﹣2;
(2)a3b﹣2a2b2+ab3.
22.(2023秋 曲靖期末)如图,在直角坐标系中,A(﹣1,5),B(﹣3,0),C(﹣4,3).
(1)在图中作出△ABC关于y轴对称的图形△A1B1C1;
(2)写出点A1,B1,C1的坐标;
(3)求△ABC的面积.
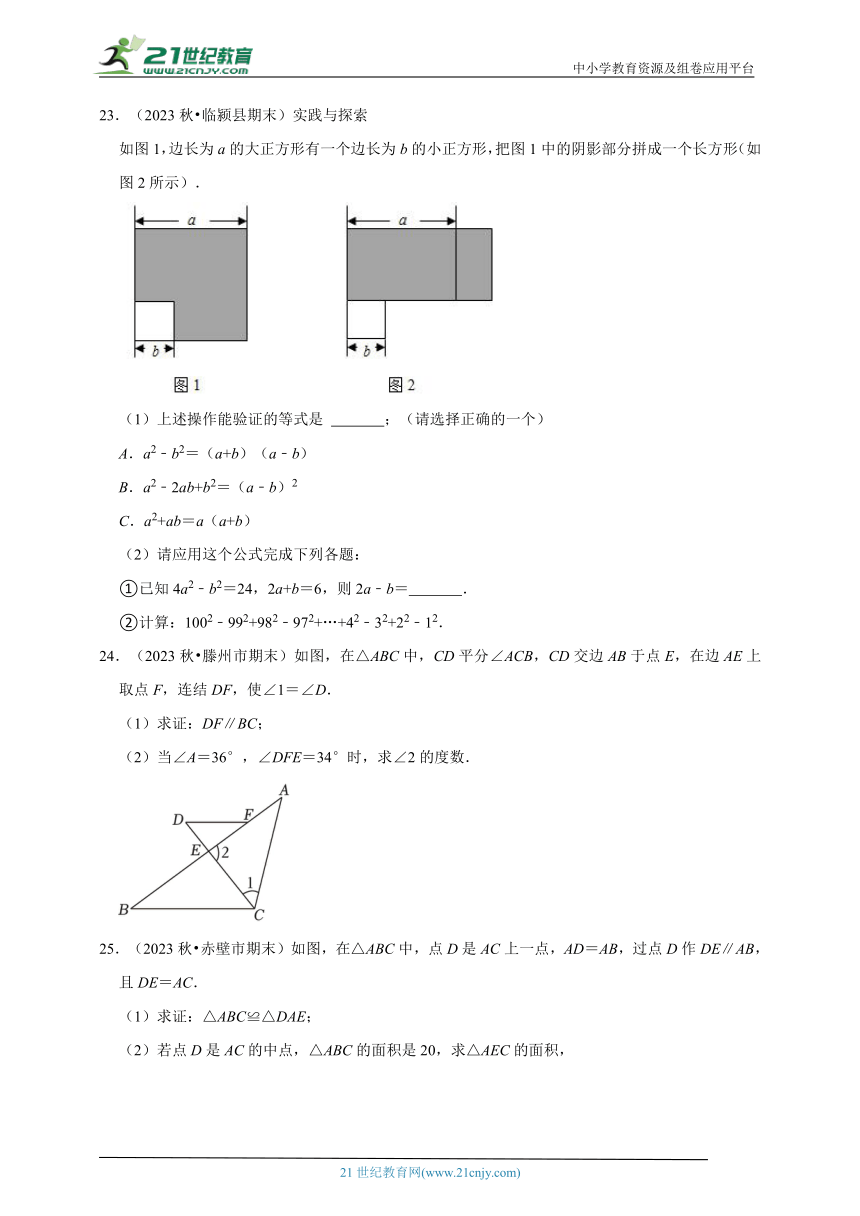
23.(2023秋 临颍县期末)实践与探索
如图1,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A.a2﹣b2=(a+b)(a﹣b)
B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b)
(2)请应用这个公式完成下列各题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= .
②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12.
24.(2023秋 滕州市期末)如图,在△ABC中,CD平分∠ACB,CD交边AB于点E,在边AE上取点F,连结DF,使∠1=∠D.
(1)求证:DF∥BC;
(2)当∠A=36°,∠DFE=34°时,求∠2的度数.
25.(2023秋 赤壁市期末)如图,在△ABC中,点D是AC上一点,AD=AB,过点D作DE∥AB,且DE=AC.
(1)求证:△ABC≌△DAE;
(2)若点D是AC的中点,△ABC的面积是20,求△AEC的面积,
26.(2023秋 佛山期末)已知∠AOB=90°,直线CD与OA交于点C,与OB交于点D,点C,D均不与点O重合,CE平分∠DCO,DE平分∠CDO.
(1)如图1,当∠OCD=40°时,求∠CED的度数;
(2)如图2,延长CE与BO交于点F,过E作射线EG与CD交于点G,且满足∠CFO﹣∠GED=45°.求证:GE∥DO;
(3)如图3,过点C作CM⊥CN,MN是∠COD的外角平分线所在直线,与射线CE交于点N,与CM交于点M.在△CMN中,如果有一个角的度数是另一个角的3倍,请直接写出∠CDE的度数.
27.(2023秋 香河县期末)【学科融合】如图1,在反射现象中,反射光线,入射光线和法线都在同一个平面内;反射光线和入射光线分别位于法线两侧;反射角r等于入射角i.这就是光的反射定律.
【问题解决】如图2.小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜,手电简的灯泡在点G处,手电简的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处,点F到地面的高度CF=1.5m,点A、点C到平面镜B点的距离相等.图中点A,B,C,D在同一条直线上.求灯泡到地面的高度AG.
期末真题重组卷-2024-2025学年数学八年级上册人教版
参考答案与试题解析
一.选择题(共10小题)
1.(2023秋 南充期末)体育是一个锻炼身体,增强体质,培养道德和意志品质的教育过程,是培养全面发展的人的一个重要方面,下列体育图标是轴对称图形的是( )
A. B.
C. D.
【解答】解:A.图形不是轴对称图形,不符合题意;
B.图形不是轴对称图形,不符合题意;
C.图形是轴对称图形,符合题意;
D.图形不是轴对称图形,不符合题意.
故选:C.
2.(2024春 晋江市期末)空调安装在墙上时,一般都会采用如图的方法固定,这种方法应用的几何原理是( )
A.两点确定一条直线 B.两点之间线段最短
C.三角形的稳定性 D.垂线段最短
【解答】解:这种方法应用的数学知识是:三角形的稳定性,
故选:C.
3.(2023秋 汕尾期末)如果将一副三角板按如图的方式叠放,则∠1的度数为( )
A.105° B.120° C.75° D.45°
【解答】解:由三角形的外角性质可得:∠1=(90°﹣45°)+60°=105°,
故选:A.
4.(2023秋 赣县区期末)点(﹣2,3)关于x轴的对称点的坐标为( )
A.(﹣2,﹣3) B.(2,3) C.(﹣2,3) D.(2,﹣3)
【解答】解:点(﹣2,3)关于x轴的对称点的坐标是(﹣2,﹣3).
故选:A.
5.(2023秋 德庆县期末)如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )
A.6米 B.9米 C.12米 D.15米
【解答】解:如图,根据题意BC=3米,
∵∠BAC=30°,
∴AB=2BC=2×3=6(米),
∴3+6=9(米).
故选:B.
6.(2023秋 高邮市期末)如图,已知三角形卡纸的三边长分别为6cm、8cm、10cm,要将这张卡纸剪成两个三角形,且其中必须有一个三角形是等腰三角形,在用不同剪法剪得的这些等腰三角形中,腰长的最小值为( )
A. B.5cm C. D.6cm
【解答】解:如图所示,当△ABD为等腰三角形时,腰长AB=AD=6cm;
当△BCD为等腰三角形时,腰长BC=CD=8cm;
∵三角形卡纸的三边长分别为6cm、8cm、10cm,
∴62+82=102,
∴△ABC为直角三角形,
当△BCD与△ABD都是等腰三角形时,腰长AD=BD=CD=5cm;
∴腰长的最小值为5cm.
故选:B.
7.(2023秋 双辽市期末)如图,在△ABC中,AC=18cm,BC=20cm,点M从点A出发以每秒2cm的速度向点C运动,点N从点C出发以每秒1.6cm的速度向点B运动,其中一个动点到达终点时,另一个动点也随之停止运动,当△CMN是以MN为底的等腰三角形时,则这时等腰三角形的腰长是( )
A.5cm B.6cm C.7cm D.8cm
【解答】解:设运动的时间为x秒,
在△ABC中,BC=20cm,AC=18cm,
点M从点A出发以每秒2cm的速度向点C运动,点N从点C出发以每秒1.6cm的速度向点B运动,
当△CMN是等腰三角形时,CM=CN,
CM=18﹣2x,CN=1.6x
即18﹣2x=1.6x,
解得x=5.
∴CM=CN=8(cm),
故选:D.
8.(2017秋 嘉兴期末)用尺规作图作∠BAC的平分线AD,痕迹如图所示,则此作图的依据是( )
A.SAS B.SSS C.ASA D.AAS
【解答】解:根据尺规作图的过程可知:
三边对应相等的三角形全等,
全等三角形的对应角相等.
故选:B.
9.(2023秋 香洲区期末)如图,在等边△ABC中,E为AB上一点,过点E的直线交AC于点F,交BC延长线于点D,作EG⊥AC垂足为G,如 AE=CD,AB=α,则GF的长为( )
A. B. C. D.
【解答】解:如图,过点E作EM∥BC,交AC于点M,
∴∠FEM=∠D,∠FME=∠FCD,∠AEM=∠B,∠AME=∠ACB,
∵△ABC是等边三角形,
∴∠B=∠ACB=60°,
∴∠AEM=AME=60°,
∴△AEM是等边三角形,
∴AE=EM,
∵AE=CD,
∴EM=CD,
在△MEF和△CDF中,
,
∴△MEF≌△CDF(ASA),
∴FM=FC=CM,
∵△ABC等边三角形,
∴AC=AB=a,
∵AE=EM,EG⊥AC,
∴GM=AG=AM,
∴GF=GM+FM=AM+CM=(AM+CM)=AC=a,
故选:C.
10.(2023秋 荣昌区校级期末)若关于x的一元一次不等式组无解,且关于y的分式方程有非负整数解,则符合条件的所有整数a的和为( )
A.7 B.8 C.14 D.15
【解答】解:解不等式组,得,
∵不等式组无解,
∴a﹣1≤6,
∴a≤7.
解分式方程,得y=,
∵y=为非负整数,a≤7,
∴a=﹣1或1或3或5或7,
∵a=1时,y=1,原分式方程无解,故将a=1舍去,
∴符合条件的所有整数a的和是﹣1+3+5+7=14,
故选:C.
二.填空题(共8小题)
11.(2023秋 固始县期末)如图,将四边形ABCD去掉一个70°的角得到一个五边形BCDEF,则∠1+∠2= 250 °.
【解答】解:∵∠A=70°,
∴在△AEF中,∠AEF+∠AFE=180°﹣∠A=110°,
∴∠1+∠2=360°﹣110°=250°,
故答案为:250.
12.(2023秋 浉河区期末)如图,B、E、C、F四点在同一直线上,且BE=CF,AC=DF,添加一个条件 AB=DE(答案不唯一) ,使△ABC≌△DEF(写出一个即可).
【解答】解:添加AB=DE(答案不唯一),
证明如下:∵BE=CF,
∴BE+EC=CF+EC,
即BC=FE,
∵AC=DF,AB=DE,
∴△ABC≌△DEF(SSS),
故答案为:AB=DE(答案不唯一).
13.(2023春 武功县期末)如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=5,若点Q是射线OB上一点,OQ=4,则△ODQ的面积是 10 .
【解答】解:作DH⊥OB于点H,
∵OC是∠AOB的角平分线,DP⊥OA,DH⊥OB,
∴DH=DP=5,
∴△ODQ的面积=OQ DH=4×5=10,
故答案为:10.
14.(2023秋 福田区校级期末)已知P1(a﹣1,5)和P2(2,b﹣1)关于x轴对称,则(a+b)2024的值为 1 .
【解答】解:∵P1(a﹣1,5)和P2(2,b﹣1)关于x轴对称,
∴a﹣1=2,b﹣1=﹣5,
∴a=3,b=﹣4,
∴(a+b)2024=(3﹣4)2024=(﹣1)2024=1,
故答案为:1.
15.(2024春 滕州市期末)如图,△ABC中,AB=AC=13,BC=10,AD是BC边上的中线且AD=12,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为 .
【解答】解:作E关于AD的对称点M,连接CM交AD于F,连接EF,过C作CN⊥AB于N,
∵AB=AC=13,BC=10,AD是BC边上的中线,
∴BD=DC=5,AD⊥BC,AD平分∠BAC,
∴M在AB上,
在Rt△ABD中,AD=12,
∴S△ABC=×BC×AD=×AB×CN,
∴CN===,
∵E关于AD的对称点M,
∴EF=FM,
∴CF+EF=CF+FM=CM,
根据垂线段最短得出:CM≥CN,
即CF+EF≥,
即CF+EF的最小值是,
故答案为:.
16.(2024春 冷水滩区期末)若x2+2(m﹣3)x+16是完全平方式,则m的值等于 7或﹣1 .
【解答】解:∵x2+2(m﹣3)x+16是完全平方式,
∴2(m﹣3)x=±2 x 4,
解得:m=7或﹣1,
故答案为:7或﹣1.
17.(2024春 太平区期末)已知关于x的分式方程﹣2=的解是非负数,则m的取值范围是 m≤5且m≠3 .
【解答】解:去分母得:1﹣m﹣2(x﹣1)=﹣2,
化简得:2x=5﹣m,
∴x=,
∵分式方程的解为非负数,
∴≥0,
∴m≤5,
又x=≠1,
∴m≠3,
故答案为:m≤5且m≠3.
18.(2023秋 西城区期末)甲、乙两名同学作为志愿者帮助图书馆清点一批图书,甲3h清点完这批图书的,乙加入清点剩余的图书,两人合作2.4h清点完剩余的图书.如果乙单独清点这批图书需要几小时?若设乙单独清点这批图书需要xh,则根据题意可列方程为 2.4×(+)= .
【解答】解:设乙单独清点这批图书需要x小时,
根据题意,得2.4×(+)=,
故答案为:2.4×(+)=.
三.解答题(共9小题)
19.(2023秋 门头沟区期末)解分式方程:.
【解答】解:方程两边都乘以最简公分母x(x+2),
得(x﹣1)(x+2)+3x=x(x+2),
解这个方程,得:x=1,
检验:当x=1时,最简公分母x(x+2)≠0,
∴原方程的解是x=1.
20.(2022秋 顺庆区校级期末)先化简代数式,再从2,﹣2,1,﹣1四个数中选择一个你喜欢的数代入求值.
【解答】解:原式=÷
=
=,
∵a+2≠0,a﹣2≠0,a﹣1≠0,
∴a只能取﹣1,
当a=﹣1时,原式==.
21.(2023秋 重庆期末)因式分解:
(1)8a2﹣2;
(2)a3b﹣2a2b2+ab3.
【解答】解:(1)原式=2(4a2﹣1)
=2(2a+1)(2a﹣1);
(2)原式=ab(a2﹣2ab+b2)
=ab(a﹣b)2.
22.(2023秋 曲靖期末)如图,在直角坐标系中,A(﹣1,5),B(﹣3,0),C(﹣4,3).
(1)在图中作出△ABC关于y轴对称的图形△A1B1C1;
(2)写出点A1,B1,C1的坐标;
(3)求△ABC的面积.
【解答】解:(1)如图,△A1B1C1即为所求;
(2)A1(1,5),B1(3,0),C1(4,3);
(3)△ABC的面积为:3×5﹣2×5﹣1×3﹣2×3=.
23.(2023秋 临颍县期末)实践与探索
如图1,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 A ;(请选择正确的一个)
A.a2﹣b2=(a+b)(a﹣b)
B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b)
(2)请应用这个公式完成下列各题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= 4 .
②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12.
【解答】解:(1)图1中阴影部分的面积为两个正方形的面积差,即a2﹣b2,
图2中的阴影部分是长为(a+b),宽为(a﹣b)的长方形,因此面积为(a+b)(a﹣b),
所以有a2﹣b2=(a+b)(a﹣b),
故答案为:A;
(2)①∵4a2﹣b2=24,
∴(2a+b)(2a﹣b)=24,
又∵2a+b=6,
∴6(2a﹣b)=24,
即2a﹣b=4,
故答案为:4;
②∵1002﹣992=(100+99)(100﹣99)=100+99,
982﹣972=(98+97)(98﹣97)=98+97,
…
22﹣12=(2+1)(2﹣1)=2+1,
∴原式=100+99+98+97+…+4+3+2+1=5050.
24.(2023秋 滕州市期末)如图,在△ABC中,CD平分∠ACB,CD交边AB于点E,在边AE上取点F,连结DF,使∠1=∠D.
(1)求证:DF∥BC;
(2)当∠A=36°,∠DFE=34°时,求∠2的度数.
【解答】(1)证明:∵CD平分∠ACB,
∴∠DCB=∠1,
∵∠1=∠D,
∴∠DCB=∠D,
∴DF∥BC;
(2)解:∵DF∥BC,∠DFE=34°,
∴∠B=∠DFE=34°,
在△ABC中,∠A=36°,∠B=34°,
∴∠ACB=180°﹣36°﹣34°=110°,
∵CD平分∠ACB,
,
∴∠2=180°﹣36°﹣55°=89°.
25.(2023秋 赤壁市期末)如图,在△ABC中,点D是AC上一点,AD=AB,过点D作DE∥AB,且DE=AC.
(1)求证:△ABC≌△DAE;
(2)若点D是AC的中点,△ABC的面积是20,求△AEC的面积,
【解答】解:(1)证明:∵DE∥AB,
∴∠BAC=∠ADE,
在△ABC和△DAE中,
∴△ABC≌△DAE(SAS);
(2)∵△ABC≌△DAE,
∴S△ABC=S△DAE=20,
点D是AC的中点,
∴S△AEC=2S△DAE=2×20=40
26.(2023秋 佛山期末)已知∠AOB=90°,直线CD与OA交于点C,与OB交于点D,点C,D均不与点O重合,CE平分∠DCO,DE平分∠CDO.
(1)如图1,当∠OCD=40°时,求∠CED的度数;
(2)如图2,延长CE与BO交于点F,过E作射线EG与CD交于点G,且满足∠CFO﹣∠GED=45°.求证:GE∥DO;
(3)如图3,过点C作CM⊥CN,MN是∠COD的外角平分线所在直线,与射线CE交于点N,与CM交于点M.在△CMN中,如果有一个角的度数是另一个角的3倍,请直接写出∠CDE的度数.
【解答】(1)解:∵∠OCD=40°,∠AOB=90°,
∴∠CDO=50°,
∵CE平分∠DCO,DE平分∠CDO,
∴∠DCE=∠OCE=∠DCO,∠CDE=∠ODE=∠CDO,
∴∠DCE=20°,∠CDE=25°,
∴∠CED=180°﹣∠DCE﹣∠CDE=135°;
(2)证明:∵CE平分∠DCO,DE平分∠CDO,
∴∠DCE=∠OCE=∠DCO,∠CDE=∠ODE=∠CDO,
∴∠CED=180°﹣∠DCE﹣∠CDE
=180°﹣(∠DCO+∠CDO)
=180°﹣(180°﹣∠O)
=180°﹣90°+∠O
=90°+45°
=135°.
∵∠CED=∠CFD+∠EDF,∠CFD=180°﹣∠CFO,
∴∠CED=180°﹣∠CFO+∠EDF,
∵∠CFO﹣∠GED=45°,
∴∠CFO=∠GED+45°,
∴∠CED=180°﹣(∠GED+45°)+∠EDF,
∴135°=∠180°﹣∠GED﹣45°+∠EDF,
∴∠GED=∠EDF,
∴GE∥DO;
(3)解:①当∠MCN=3∠N时,
∵CM⊥CN,
∴∠MCN=90°,
∴∠N=∠MCN=30°,
∴∠M=60°.
∵∠COD=90°,
∴∠DON=45°,
∴∠COM=45°.
∴∠MCO=180°﹣∠M﹣∠COM=75°.
∴∠NCO=90°﹣∠MCO=15°.
∵CE平分∠DCO,
∴∠DCO=2∠NCO=30°,
∴∠CDO=90°﹣∠DCO=60°,
∵DE平分∠CDO,
∴∠CDE=∠CDO=30°;
②当∠M=3∠N时,
∵CM⊥CN,
∴∠MCN=90°,
∴∠M+∠N=90°,
∴∠N=22.5°,∠M=67.5°,
∵∠COD=90°,
∴∠DON=45°,
∴∠COM=45°.
∴∠MCO=180°﹣∠M﹣∠COM=67.5°.
∴∠NCO=90°﹣∠MCO=22.5°.
∵CE平分∠DCO,
∴∠DCO=2∠NCO=45°,
∴∠CDO=90°﹣∠DCO=45°,
∵DE平分∠CDO,
∴∠CDE=∠CDO=22.5°.
综上,在△CMN中,如果有一个角的度数是另一个角的3倍,∠CDE的度数为30°或22.5°.
27.(2023秋 香河县期末)【学科融合】如图1,在反射现象中,反射光线,入射光线和法线都在同一个平面内;反射光线和入射光线分别位于法线两侧;反射角r等于入射角i.这就是光的反射定律.
【问题解决】如图2.小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜,手电简的灯泡在点G处,手电简的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处,点F到地面的高度CF=1.5m,点A、点C到平面镜B点的距离相等.图中点A,B,C,D在同一条直线上.求灯泡到地面的高度AG.
【解答】解:如图2,根据题意得:法线垂直于平面镜,且∠i=∠r,
∴∠ABG=∠FBC,
在△FCB和△GAB中,
,
∴△FCB≌△GAB(ASA),
∴AG=CF=1.5m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题重组卷-2024-2025学年数学八年级上册人教版
一.选择题(共10小题)
1.(2023秋 南充期末)体育是一个锻炼身体,增强体质,培养道德和意志品质的教育过程,是培养全面发展的人的一个重要方面,下列体育图标是轴对称图形的是( )
A. B.
C. D.
2.(2024春 晋江市期末)空调安装在墙上时,一般都会采用如图的方法固定,这种方法应用的几何原理是( )
A.两点确定一条直线 B.两点之间线段最短
C.三角形的稳定性 D.垂线段最短
3.(2023秋 汕尾期末)如果将一副三角板按如图的方式叠放,则∠1的度数为( )
A.105° B.120° C.75° D.45°
4.(2023秋 赣县区期末)点(﹣2,3)关于x轴的对称点的坐标为( )
A.(﹣2,﹣3) B.(2,3) C.(﹣2,3) D.(2,﹣3)
5.(2023秋 德庆县期末)如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )
A.6米 B.9米 C.12米 D.15米
6.(2023秋 高邮市期末)如图,已知三角形卡纸的三边长分别为6cm、8cm、10cm,要将这张卡纸剪成两个三角形,且其中必须有一个三角形是等腰三角形,在用不同剪法剪得的这些等腰三角形中,腰长的最小值为( )
A. B.5cm C. D.6cm
7.(2023秋 双辽市期末)如图,在△ABC中,AC=18cm,BC=20cm,点M从点A出发以每秒2cm的速度向点C运动,点N从点C出发以每秒1.6cm的速度向点B运动,其中一个动点到达终点时,另一个动点也随之停止运动,当△CMN是以MN为底的等腰三角形时,则这时等腰三角形的腰长是( )
A.5cm B.6cm C.7cm D.8cm
8.(2017秋 嘉兴期末)用尺规作图作∠BAC的平分线AD,痕迹如图所示,则此作图的依据是( )
A.SAS B.SSS C.ASA D.AAS
9.(2023秋 香洲区期末)如图,在等边△ABC中,E为AB上一点,过点E的直线交AC于点F,交BC延长线于点D,作EG⊥AC垂足为G,如 AE=CD,AB=α,则GF的长为( )
A. B. C. D.
10.(2023秋 荣昌区校级期末)若关于x的一元一次不等式组无解,且关于y的分式方程有非负整数解,则符合条件的所有整数a的和为( )
A.7 B.8 C.14 D.15
二.填空题(共8小题)
11.(2023秋 固始县期末)如图,将四边形ABCD去掉一个70°的角得到一个五边形BCDEF,则∠1+∠2= °.
12.(2023秋 浉河区期末)如图,B、E、C、F四点在同一直线上,且BE=CF,AC=DF,添加一个条件 ,使△ABC≌△DEF(写出一个即可).
13.(2023春 武功县期末)如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=5,若点Q是射线OB上一点,OQ=4,则△ODQ的面积是 .
14.(2023秋 福田区校级期末)已知P1(a﹣1,5)和P2(2,b﹣1)关于x轴对称,则(a+b)2024的值为 .
15.(2024春 滕州市期末)如图,△ABC中,AB=AC=13,BC=10,AD是BC边上的中线且AD=12,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为 .
16.(2024春 冷水滩区期末)若x2+2(m﹣3)x+16是完全平方式,则m的值等于 .
17.(2024春 太平区期末)已知关于x的分式方程﹣2=的解是非负数,则m的取值范围是 .
18.(2023秋 西城区期末)甲、乙两名同学作为志愿者帮助图书馆清点一批图书,甲3h清点完这批图书的,乙加入清点剩余的图书,两人合作2.4h清点完剩余的图书.如果乙单独清点这批图书需要几小时?若设乙单独清点这批图书需要xh,则根据题意可列方程为 .
三.解答题(共9小题)
19.(2023秋 门头沟区期末)解分式方程:.
20.(2022秋 顺庆区校级期末)先化简代数式,再从2,﹣2,1,﹣1四个数中选择一个你喜欢的数代入求值.
21.(2023秋 重庆期末)因式分解:
(1)8a2﹣2;
(2)a3b﹣2a2b2+ab3.
22.(2023秋 曲靖期末)如图,在直角坐标系中,A(﹣1,5),B(﹣3,0),C(﹣4,3).
(1)在图中作出△ABC关于y轴对称的图形△A1B1C1;
(2)写出点A1,B1,C1的坐标;
(3)求△ABC的面积.
23.(2023秋 临颍县期末)实践与探索
如图1,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A.a2﹣b2=(a+b)(a﹣b)
B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b)
(2)请应用这个公式完成下列各题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= .
②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12.
24.(2023秋 滕州市期末)如图,在△ABC中,CD平分∠ACB,CD交边AB于点E,在边AE上取点F,连结DF,使∠1=∠D.
(1)求证:DF∥BC;
(2)当∠A=36°,∠DFE=34°时,求∠2的度数.
25.(2023秋 赤壁市期末)如图,在△ABC中,点D是AC上一点,AD=AB,过点D作DE∥AB,且DE=AC.
(1)求证:△ABC≌△DAE;
(2)若点D是AC的中点,△ABC的面积是20,求△AEC的面积,
26.(2023秋 佛山期末)已知∠AOB=90°,直线CD与OA交于点C,与OB交于点D,点C,D均不与点O重合,CE平分∠DCO,DE平分∠CDO.
(1)如图1,当∠OCD=40°时,求∠CED的度数;
(2)如图2,延长CE与BO交于点F,过E作射线EG与CD交于点G,且满足∠CFO﹣∠GED=45°.求证:GE∥DO;
(3)如图3,过点C作CM⊥CN,MN是∠COD的外角平分线所在直线,与射线CE交于点N,与CM交于点M.在△CMN中,如果有一个角的度数是另一个角的3倍,请直接写出∠CDE的度数.
27.(2023秋 香河县期末)【学科融合】如图1,在反射现象中,反射光线,入射光线和法线都在同一个平面内;反射光线和入射光线分别位于法线两侧;反射角r等于入射角i.这就是光的反射定律.
【问题解决】如图2.小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜,手电简的灯泡在点G处,手电简的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处,点F到地面的高度CF=1.5m,点A、点C到平面镜B点的距离相等.图中点A,B,C,D在同一条直线上.求灯泡到地面的高度AG.
期末真题重组卷-2024-2025学年数学八年级上册人教版
参考答案与试题解析
一.选择题(共10小题)
1.(2023秋 南充期末)体育是一个锻炼身体,增强体质,培养道德和意志品质的教育过程,是培养全面发展的人的一个重要方面,下列体育图标是轴对称图形的是( )
A. B.
C. D.
【解答】解:A.图形不是轴对称图形,不符合题意;
B.图形不是轴对称图形,不符合题意;
C.图形是轴对称图形,符合题意;
D.图形不是轴对称图形,不符合题意.
故选:C.
2.(2024春 晋江市期末)空调安装在墙上时,一般都会采用如图的方法固定,这种方法应用的几何原理是( )
A.两点确定一条直线 B.两点之间线段最短
C.三角形的稳定性 D.垂线段最短
【解答】解:这种方法应用的数学知识是:三角形的稳定性,
故选:C.
3.(2023秋 汕尾期末)如果将一副三角板按如图的方式叠放,则∠1的度数为( )
A.105° B.120° C.75° D.45°
【解答】解:由三角形的外角性质可得:∠1=(90°﹣45°)+60°=105°,
故选:A.
4.(2023秋 赣县区期末)点(﹣2,3)关于x轴的对称点的坐标为( )
A.(﹣2,﹣3) B.(2,3) C.(﹣2,3) D.(2,﹣3)
【解答】解:点(﹣2,3)关于x轴的对称点的坐标是(﹣2,﹣3).
故选:A.
5.(2023秋 德庆县期末)如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )
A.6米 B.9米 C.12米 D.15米
【解答】解:如图,根据题意BC=3米,
∵∠BAC=30°,
∴AB=2BC=2×3=6(米),
∴3+6=9(米).
故选:B.
6.(2023秋 高邮市期末)如图,已知三角形卡纸的三边长分别为6cm、8cm、10cm,要将这张卡纸剪成两个三角形,且其中必须有一个三角形是等腰三角形,在用不同剪法剪得的这些等腰三角形中,腰长的最小值为( )
A. B.5cm C. D.6cm
【解答】解:如图所示,当△ABD为等腰三角形时,腰长AB=AD=6cm;
当△BCD为等腰三角形时,腰长BC=CD=8cm;
∵三角形卡纸的三边长分别为6cm、8cm、10cm,
∴62+82=102,
∴△ABC为直角三角形,
当△BCD与△ABD都是等腰三角形时,腰长AD=BD=CD=5cm;
∴腰长的最小值为5cm.
故选:B.
7.(2023秋 双辽市期末)如图,在△ABC中,AC=18cm,BC=20cm,点M从点A出发以每秒2cm的速度向点C运动,点N从点C出发以每秒1.6cm的速度向点B运动,其中一个动点到达终点时,另一个动点也随之停止运动,当△CMN是以MN为底的等腰三角形时,则这时等腰三角形的腰长是( )
A.5cm B.6cm C.7cm D.8cm
【解答】解:设运动的时间为x秒,
在△ABC中,BC=20cm,AC=18cm,
点M从点A出发以每秒2cm的速度向点C运动,点N从点C出发以每秒1.6cm的速度向点B运动,
当△CMN是等腰三角形时,CM=CN,
CM=18﹣2x,CN=1.6x
即18﹣2x=1.6x,
解得x=5.
∴CM=CN=8(cm),
故选:D.
8.(2017秋 嘉兴期末)用尺规作图作∠BAC的平分线AD,痕迹如图所示,则此作图的依据是( )
A.SAS B.SSS C.ASA D.AAS
【解答】解:根据尺规作图的过程可知:
三边对应相等的三角形全等,
全等三角形的对应角相等.
故选:B.
9.(2023秋 香洲区期末)如图,在等边△ABC中,E为AB上一点,过点E的直线交AC于点F,交BC延长线于点D,作EG⊥AC垂足为G,如 AE=CD,AB=α,则GF的长为( )
A. B. C. D.
【解答】解:如图,过点E作EM∥BC,交AC于点M,
∴∠FEM=∠D,∠FME=∠FCD,∠AEM=∠B,∠AME=∠ACB,
∵△ABC是等边三角形,
∴∠B=∠ACB=60°,
∴∠AEM=AME=60°,
∴△AEM是等边三角形,
∴AE=EM,
∵AE=CD,
∴EM=CD,
在△MEF和△CDF中,
,
∴△MEF≌△CDF(ASA),
∴FM=FC=CM,
∵△ABC等边三角形,
∴AC=AB=a,
∵AE=EM,EG⊥AC,
∴GM=AG=AM,
∴GF=GM+FM=AM+CM=(AM+CM)=AC=a,
故选:C.
10.(2023秋 荣昌区校级期末)若关于x的一元一次不等式组无解,且关于y的分式方程有非负整数解,则符合条件的所有整数a的和为( )
A.7 B.8 C.14 D.15
【解答】解:解不等式组,得,
∵不等式组无解,
∴a﹣1≤6,
∴a≤7.
解分式方程,得y=,
∵y=为非负整数,a≤7,
∴a=﹣1或1或3或5或7,
∵a=1时,y=1,原分式方程无解,故将a=1舍去,
∴符合条件的所有整数a的和是﹣1+3+5+7=14,
故选:C.
二.填空题(共8小题)
11.(2023秋 固始县期末)如图,将四边形ABCD去掉一个70°的角得到一个五边形BCDEF,则∠1+∠2= 250 °.
【解答】解:∵∠A=70°,
∴在△AEF中,∠AEF+∠AFE=180°﹣∠A=110°,
∴∠1+∠2=360°﹣110°=250°,
故答案为:250.
12.(2023秋 浉河区期末)如图,B、E、C、F四点在同一直线上,且BE=CF,AC=DF,添加一个条件 AB=DE(答案不唯一) ,使△ABC≌△DEF(写出一个即可).
【解答】解:添加AB=DE(答案不唯一),
证明如下:∵BE=CF,
∴BE+EC=CF+EC,
即BC=FE,
∵AC=DF,AB=DE,
∴△ABC≌△DEF(SSS),
故答案为:AB=DE(答案不唯一).
13.(2023春 武功县期末)如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=5,若点Q是射线OB上一点,OQ=4,则△ODQ的面积是 10 .
【解答】解:作DH⊥OB于点H,
∵OC是∠AOB的角平分线,DP⊥OA,DH⊥OB,
∴DH=DP=5,
∴△ODQ的面积=OQ DH=4×5=10,
故答案为:10.
14.(2023秋 福田区校级期末)已知P1(a﹣1,5)和P2(2,b﹣1)关于x轴对称,则(a+b)2024的值为 1 .
【解答】解:∵P1(a﹣1,5)和P2(2,b﹣1)关于x轴对称,
∴a﹣1=2,b﹣1=﹣5,
∴a=3,b=﹣4,
∴(a+b)2024=(3﹣4)2024=(﹣1)2024=1,
故答案为:1.
15.(2024春 滕州市期末)如图,△ABC中,AB=AC=13,BC=10,AD是BC边上的中线且AD=12,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为 .
【解答】解:作E关于AD的对称点M,连接CM交AD于F,连接EF,过C作CN⊥AB于N,
∵AB=AC=13,BC=10,AD是BC边上的中线,
∴BD=DC=5,AD⊥BC,AD平分∠BAC,
∴M在AB上,
在Rt△ABD中,AD=12,
∴S△ABC=×BC×AD=×AB×CN,
∴CN===,
∵E关于AD的对称点M,
∴EF=FM,
∴CF+EF=CF+FM=CM,
根据垂线段最短得出:CM≥CN,
即CF+EF≥,
即CF+EF的最小值是,
故答案为:.
16.(2024春 冷水滩区期末)若x2+2(m﹣3)x+16是完全平方式,则m的值等于 7或﹣1 .
【解答】解:∵x2+2(m﹣3)x+16是完全平方式,
∴2(m﹣3)x=±2 x 4,
解得:m=7或﹣1,
故答案为:7或﹣1.
17.(2024春 太平区期末)已知关于x的分式方程﹣2=的解是非负数,则m的取值范围是 m≤5且m≠3 .
【解答】解:去分母得:1﹣m﹣2(x﹣1)=﹣2,
化简得:2x=5﹣m,
∴x=,
∵分式方程的解为非负数,
∴≥0,
∴m≤5,
又x=≠1,
∴m≠3,
故答案为:m≤5且m≠3.
18.(2023秋 西城区期末)甲、乙两名同学作为志愿者帮助图书馆清点一批图书,甲3h清点完这批图书的,乙加入清点剩余的图书,两人合作2.4h清点完剩余的图书.如果乙单独清点这批图书需要几小时?若设乙单独清点这批图书需要xh,则根据题意可列方程为 2.4×(+)= .
【解答】解:设乙单独清点这批图书需要x小时,
根据题意,得2.4×(+)=,
故答案为:2.4×(+)=.
三.解答题(共9小题)
19.(2023秋 门头沟区期末)解分式方程:.
【解答】解:方程两边都乘以最简公分母x(x+2),
得(x﹣1)(x+2)+3x=x(x+2),
解这个方程,得:x=1,
检验:当x=1时,最简公分母x(x+2)≠0,
∴原方程的解是x=1.
20.(2022秋 顺庆区校级期末)先化简代数式,再从2,﹣2,1,﹣1四个数中选择一个你喜欢的数代入求值.
【解答】解:原式=÷
=
=,
∵a+2≠0,a﹣2≠0,a﹣1≠0,
∴a只能取﹣1,
当a=﹣1时,原式==.
21.(2023秋 重庆期末)因式分解:
(1)8a2﹣2;
(2)a3b﹣2a2b2+ab3.
【解答】解:(1)原式=2(4a2﹣1)
=2(2a+1)(2a﹣1);
(2)原式=ab(a2﹣2ab+b2)
=ab(a﹣b)2.
22.(2023秋 曲靖期末)如图,在直角坐标系中,A(﹣1,5),B(﹣3,0),C(﹣4,3).
(1)在图中作出△ABC关于y轴对称的图形△A1B1C1;
(2)写出点A1,B1,C1的坐标;
(3)求△ABC的面积.
【解答】解:(1)如图,△A1B1C1即为所求;
(2)A1(1,5),B1(3,0),C1(4,3);
(3)△ABC的面积为:3×5﹣2×5﹣1×3﹣2×3=.
23.(2023秋 临颍县期末)实践与探索
如图1,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是 A ;(请选择正确的一个)
A.a2﹣b2=(a+b)(a﹣b)
B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b)
(2)请应用这个公式完成下列各题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= 4 .
②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12.
【解答】解:(1)图1中阴影部分的面积为两个正方形的面积差,即a2﹣b2,
图2中的阴影部分是长为(a+b),宽为(a﹣b)的长方形,因此面积为(a+b)(a﹣b),
所以有a2﹣b2=(a+b)(a﹣b),
故答案为:A;
(2)①∵4a2﹣b2=24,
∴(2a+b)(2a﹣b)=24,
又∵2a+b=6,
∴6(2a﹣b)=24,
即2a﹣b=4,
故答案为:4;
②∵1002﹣992=(100+99)(100﹣99)=100+99,
982﹣972=(98+97)(98﹣97)=98+97,
…
22﹣12=(2+1)(2﹣1)=2+1,
∴原式=100+99+98+97+…+4+3+2+1=5050.
24.(2023秋 滕州市期末)如图,在△ABC中,CD平分∠ACB,CD交边AB于点E,在边AE上取点F,连结DF,使∠1=∠D.
(1)求证:DF∥BC;
(2)当∠A=36°,∠DFE=34°时,求∠2的度数.
【解答】(1)证明:∵CD平分∠ACB,
∴∠DCB=∠1,
∵∠1=∠D,
∴∠DCB=∠D,
∴DF∥BC;
(2)解:∵DF∥BC,∠DFE=34°,
∴∠B=∠DFE=34°,
在△ABC中,∠A=36°,∠B=34°,
∴∠ACB=180°﹣36°﹣34°=110°,
∵CD平分∠ACB,
,
∴∠2=180°﹣36°﹣55°=89°.
25.(2023秋 赤壁市期末)如图,在△ABC中,点D是AC上一点,AD=AB,过点D作DE∥AB,且DE=AC.
(1)求证:△ABC≌△DAE;
(2)若点D是AC的中点,△ABC的面积是20,求△AEC的面积,
【解答】解:(1)证明:∵DE∥AB,
∴∠BAC=∠ADE,
在△ABC和△DAE中,
∴△ABC≌△DAE(SAS);
(2)∵△ABC≌△DAE,
∴S△ABC=S△DAE=20,
点D是AC的中点,
∴S△AEC=2S△DAE=2×20=40
26.(2023秋 佛山期末)已知∠AOB=90°,直线CD与OA交于点C,与OB交于点D,点C,D均不与点O重合,CE平分∠DCO,DE平分∠CDO.
(1)如图1,当∠OCD=40°时,求∠CED的度数;
(2)如图2,延长CE与BO交于点F,过E作射线EG与CD交于点G,且满足∠CFO﹣∠GED=45°.求证:GE∥DO;
(3)如图3,过点C作CM⊥CN,MN是∠COD的外角平分线所在直线,与射线CE交于点N,与CM交于点M.在△CMN中,如果有一个角的度数是另一个角的3倍,请直接写出∠CDE的度数.
【解答】(1)解:∵∠OCD=40°,∠AOB=90°,
∴∠CDO=50°,
∵CE平分∠DCO,DE平分∠CDO,
∴∠DCE=∠OCE=∠DCO,∠CDE=∠ODE=∠CDO,
∴∠DCE=20°,∠CDE=25°,
∴∠CED=180°﹣∠DCE﹣∠CDE=135°;
(2)证明:∵CE平分∠DCO,DE平分∠CDO,
∴∠DCE=∠OCE=∠DCO,∠CDE=∠ODE=∠CDO,
∴∠CED=180°﹣∠DCE﹣∠CDE
=180°﹣(∠DCO+∠CDO)
=180°﹣(180°﹣∠O)
=180°﹣90°+∠O
=90°+45°
=135°.
∵∠CED=∠CFD+∠EDF,∠CFD=180°﹣∠CFO,
∴∠CED=180°﹣∠CFO+∠EDF,
∵∠CFO﹣∠GED=45°,
∴∠CFO=∠GED+45°,
∴∠CED=180°﹣(∠GED+45°)+∠EDF,
∴135°=∠180°﹣∠GED﹣45°+∠EDF,
∴∠GED=∠EDF,
∴GE∥DO;
(3)解:①当∠MCN=3∠N时,
∵CM⊥CN,
∴∠MCN=90°,
∴∠N=∠MCN=30°,
∴∠M=60°.
∵∠COD=90°,
∴∠DON=45°,
∴∠COM=45°.
∴∠MCO=180°﹣∠M﹣∠COM=75°.
∴∠NCO=90°﹣∠MCO=15°.
∵CE平分∠DCO,
∴∠DCO=2∠NCO=30°,
∴∠CDO=90°﹣∠DCO=60°,
∵DE平分∠CDO,
∴∠CDE=∠CDO=30°;
②当∠M=3∠N时,
∵CM⊥CN,
∴∠MCN=90°,
∴∠M+∠N=90°,
∴∠N=22.5°,∠M=67.5°,
∵∠COD=90°,
∴∠DON=45°,
∴∠COM=45°.
∴∠MCO=180°﹣∠M﹣∠COM=67.5°.
∴∠NCO=90°﹣∠MCO=22.5°.
∵CE平分∠DCO,
∴∠DCO=2∠NCO=45°,
∴∠CDO=90°﹣∠DCO=45°,
∵DE平分∠CDO,
∴∠CDE=∠CDO=22.5°.
综上,在△CMN中,如果有一个角的度数是另一个角的3倍,∠CDE的度数为30°或22.5°.
27.(2023秋 香河县期末)【学科融合】如图1,在反射现象中,反射光线,入射光线和法线都在同一个平面内;反射光线和入射光线分别位于法线两侧;反射角r等于入射角i.这就是光的反射定律.
【问题解决】如图2.小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜,手电简的灯泡在点G处,手电简的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处,点F到地面的高度CF=1.5m,点A、点C到平面镜B点的距离相等.图中点A,B,C,D在同一条直线上.求灯泡到地面的高度AG.
【解答】解:如图2,根据题意得:法线垂直于平面镜,且∠i=∠r,
∴∠ABG=∠FBC,
在△FCB和△GAB中,
,
∴△FCB≌△GAB(ASA),
∴AG=CF=1.5m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
