1-5单元阶段测试卷(含解析)-数学六年级上册苏教版
文档属性
| 名称 | 1-5单元阶段测试卷(含解析)-数学六年级上册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 512.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-07 10:10:55 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
1-5单元阶段测试卷-数学六年级上册苏教版
一、选择题
1.现有190张铁皮做盒子,每张铁皮做8个盒身或做22个盒底,而1个盒身与2个盒底配成1个盒子,则用( )张铁皮做盒身。
A.80 B.100 C.110 D.90
2.一根3米长的绳子,第一次用去,第二次用去米,两次用去的长度相比,( )。
A.第一次长 B.第二次长 C.一样长 D.无法比较
3.文具里有蓝、黄两种铅笔出售,蓝铅笔3元4支,黄铅笔4元3支,蓝、黄两种铅笔的单价比是( )。
A.16∶9 B.9∶16 C.1∶1 D.无法比较
4.如果7-(÷□+)=5,那么□=( )。
A. B. C. D.
5.如图所示,明明在一个长方体玻璃容器中摆了若干个体积为1立方厘米的小正方体。由此可知,这个玻璃容器的容积是( )立方厘米。
A.72 B.84 C.90 D.95
6.一个正方体的表面积是24cm2,如果底面不变,高度增加3cm,体积增加( )cm3。
A.4 B.24 C.56 D.12
二、填空题
7.一台电视机降价,是把( )看作单位“1”。如果原价是3600元,那么现在降价了( )元,现价是( )元。
8.5个大盒和2个小盒共装了240个球,每个大盒比每个小盒多装20个。每个大盒装( )个球,每个小盒装( )个球。
9.妈妈买来猕猴桃和柠檬共60个,其中猕猴桃占,吃去( )个柠檬后,猕猴桃与柠檬的个数比是4∶5。
10.如图是用棱长1厘米的正方体木块摆成的几何体,它的体积是( )立方厘米,表面积是( )平方厘米。
11.一个分数与它本身相加、相减、相除,把所得的和、差、商相加,结果是,这个分数是。
12.明明要围一个棱长5分米的正方体框架,他至少要准备一根( )分米长的铁丝。
13.春节前夕,小红用一根长120厘米的铁丝做一个长方体灯笼的框架,他的长、宽、高的比是2∶1∶3,在这个灯笼框架的侧面糊上彩纸,彩纸的面积至少是( )平方厘米。这个灯笼的框架的体积是( )立方厘米。
14.小明和小刚共收集121张卡片,已知小明卡片数量的和小刚卡片数量的相等。小明收集了( )张卡片,小刚收集了( )张卡片。
三、判断题
15.假分数的倒数都比原数大。( )
16.1箱苹果比1箱橘子重5千克,那么5箱苹果比5箱橘子重5千克。( )
17.。( )
18.搭一个正方体需要12根长短相等的小棒和8个橡皮泥小球。( )
19.无论大小,圆的周长与直径的比值都相等。( )
四、计算题
20.直接写出得数。
3.5+0.8= 3-1.6= 0.23÷0.1= 3.14×4=
21.计算下面各题。(能简算的要用简便方法算)
22.解方程。
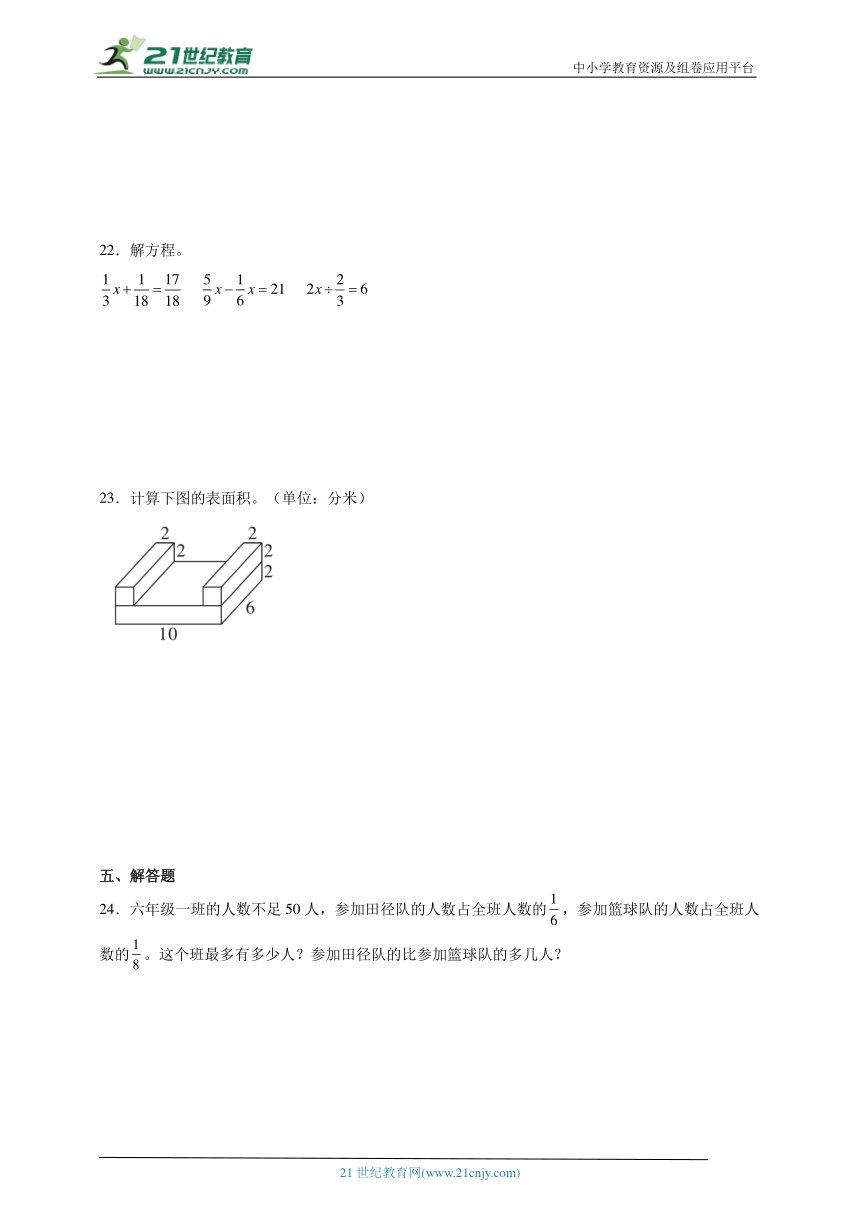
23.计算下图的表面积。(单位:分米)
五、解答题
24.六年级一班的人数不足50人,参加田径队的人数占全班人数的,参加篮球队的人数占全班人数的。这个班最多有多少人?参加田径队的比参加篮球队的多几人?
25.“五一”节活动期间,王阿姨在京东自营店为公司买了垃圾桶和文件框共花了180元,每个垃圾桶20元,每个文件框10元,买的文件框比垃圾桶多6个。王阿姨买了垃圾桶和文件框分别多少个?
26.一种混凝土是将水泥、黄沙、石子按1∶2∶4拌成的,现有水泥5.4吨,应再运来多少吨黄沙和石子才能正好拌成这种混凝土?
27.某汽车厂去年计划生产汽车12600辆,结果上半年完成了全年计划的,下半年完成全年计划的。全年超产汽车多少辆?
28.一间长方体形状的教室,长8米,宽6米,高3米,门窗面积共14平方米。要粉刷教室的四壁和天花板,如果每平方米用涂料0.25千克,共需要涂料多少千克?
29.王大伯按照下图裁剪一块长方形铁皮,焊接成一个底面是正方形的无盖长方体。这个长方体容器的容积是多少毫升?
参考答案:
题号 1 2 3 4 5 6
答案 C A B B A D
1.C
【分析】先设x张铁皮做盒身,则(190-x)张铁皮做盒底。根据题意可知,一个盒身需要两个盒底,每张铁皮做8个盒身或做22个盒底,所以得出方程式为:2×8x=22(190-x),解出x即可。
【详解】解:设x张铁皮做盒身,则(190-x)张铁皮做盒底。
2×8x=22(190-x)
16x=4180-22x
16x+22x=4180-22x+22x
38x=4180
38x÷38=4180÷38
x=110
用110张铁皮做盒身。
故答案为:C
2.A
【分析】把绳子的长度看作单位“1”,第一次用去,用绳子的长度×,求出第一次用去的长度,再和第二次用去的长度进行比较,即可解答。
【详解】3×=1(米)
1>,第一次长。
一根3米长的绳子,第一次用去,第二次用去米,两次用去的长度相比,第一次长。
故答案为:A
3.B
【分析】根据总价÷数量=单价,据此分别求出蓝铅笔和黄铅笔的单价,再写出它们的单价比,最后化简为最简整数比。
【详解】蓝铅笔的单价:3÷4=(元)
黄铅笔的单价:4÷3=(元)
蓝铅笔的单价与黄铅笔的单价比:
∶
=(×12)∶(×12)
=9∶16
故答案为:B
4.B
【分析】7-(÷□+)=5根据题目可知,7减去括号里的数等于5,则括号里的数是:7-5=2,即÷□+=2,把□可以当成一个x,即÷x+=2,根据等式的性质1和等式的性质2解出x的值即□的值。
【详解】由分析可知,把□看成x
即原式变为:7-(÷x+)=5
解:÷x+=7-5
÷x+=2
÷x=2-
÷x=
x=÷
x=
故答案为:B。
【点睛】本题主要考查解方程,熟练掌握等式的性质1和等式的性质2,并灵活运用。
5.A
【分析】根据正方体的体积公式V=a3,可知体积为1立方厘米的小正方体的棱长是1厘米。
观察图形可知,长方体玻璃容器的长、宽、高分别摆有6个、4个、3个小正方体,所以它的长是6厘米,宽是4厘米,高是3厘米;根据长方体的体积(容积)公式V=abh,即可求出这个玻璃容器的容积。
【详解】因为1=1×1×1,所以体积为1立方厘米的小正方体的棱长是1厘米。
6×4×3
=24×3
=72(立方厘米)
这个玻璃容器的容积是72立方厘米。
故答案为:A
6.D
【分析】根据正方体的表面积公式S=6a2,可得出正方体的底面积,如果底面不变,高度增加3cm,增加的体积=正方体底面积×增加的高,据此作答。
【详解】24÷6×3
=4×3
=12(cm3)
故答案为:D
【点睛】本题考查正方体表面积和长方体体积公式的灵活运用,关键是求出正方体的底面积。
7. 原价 1600 2000
【分析】由题意可知,把原价看作单位“1”,根据求一个数的几分之几是多少,用乘法计算,用原价乘,得到降价的钱数,再用原价减降价的钱数,可得现价。
【详解】(元)
(元)
一台电视机降价,是把原价看作单位“1”。如果原价是3600元,那么现在降价了1600元,现价是2000元。
8. 40 20
【分析】240个球再增加2×20=40个球,就是7个大盒共装求的个数(240+40=280个),由此得出每个大盒装280÷7=40个球,进而可得每个小盒装40-20=20个球;据此解答。
【详解】(240+20×2)÷(5+2)
=280÷7
=40(个)
40-20=20(个)
【点睛】理解“240个球再增加2×20=40个球,就是7个大盒共装求的个数(240+40=280个)”是解题的关键。
9.6
【分析】已知猕猴桃和柠檬共60个,其中猕猴桃占,根据求一个数的几分之几是多少,用猕猴桃和柠檬的总数乘,求出猕猴桃的个数;再用总数减去猕猴桃的个数,即是柠檬原有的个数;已知吃去若干个柠檬后,猕猴桃与柠檬的个数比是4∶5,即柠檬剩下的个数占猕猴桃的,把猕猴桃的个数看作单位“1”,单位“1”已知,用猕猴桃的个数乘,求出柠檬剩下的个数;最后用柠檬原有的个数减去剩下的个数,即是吃掉柠檬的个数。
【详解】猕猴桃:60×=24(个)
原有柠檬:60-24=36(个)
吃去几个柠檬后还剩下的柠檬:
24×=30(个)
吃去的柠檬:36-30=6(个)
所以,吃去6个柠檬后,猕猴桃与柠檬的个数比是4∶5。
10. 15 46
【分析】根据正方体的体积公式V=a3,可知棱长1厘米的正方体的体积是1立方厘米;从图中数出正方体的个数,再乘用正方体的体积,即是这个几何体的体积。
已知正方体的棱长是1厘米,那么正方体一个面的面积是1平方厘米。求这个几何体的表面积,就是求露出正方体的面的面积之和,分别数出从上下面、前后面、左右面看到的小正方形的个数,再乘一个面的面积即可。
【详解】1×1×1×15=15(立方厘米)
(9+7+7)×2
=23×2
=46(个)
1×1×46=46(平方厘米)
它的体积是15立方厘米,表面积是46平方厘米。
11.
【分析】一个数+它本身=这个数的2倍,一个数-它本身=0,一个数÷它本身=1,据此用(和、差、商相加的结果-1)=这个分数的2倍,再除以2就是这个分数。
【详解】(-1)÷2
=÷2
=×
=
这个分数是。
【点睛】关键是明确特殊的加、减和除法的结果,掌握分数除法的计算方法。
12.60
【分析】根据题意,用一根铁丝围成一个正方体框架,那么铁丝的长度等于正方体的棱长总和;根据正方体的棱长总和=棱长×12,代入数据计算,求出铁丝的长度。
【详解】5×12=60(分米)
他至少要准备一根60分米长的铁丝。
13. 450 750
【分析】根据按比例分配,先求出小红做的长方体灯笼的长、宽、高的长度;侧面糊上彩纸,就是长方体表面积去掉上下两个面,根据表面积公式:(宽×高+长×高)×2,代入数据,求出侧面积;再根据长方体的体积公式:长×宽×高,代入数据,即可解答。
【详解】长:120÷4×
=30×
=10(厘米)
宽:120÷4×
=30×
=5(厘米)
高:120÷4×
=30×
=15(厘米)
侧面积:(5×15+10×15)×2
=(75+150)×2
=225×2
=450(平方厘米)
体积:10×5×15
=50×15
=750(立方厘米)
【点睛】本题考查长方体的特征,长方体表面积公式、体积公式的应用;以及按比例分配问题。
14. 55 66
【分析】先确定两人卡片数量比,总数量÷总份数,求出一份数,一份数分别乘两人对应份数即可。
【详解】小明卡片数量×=小刚卡片数量×
小明卡片数量∶小刚卡片数量=5∶6
121÷(5+6)
=121÷11
=11(张)
11×5=55(张)
11×6=66(张)
【点睛】关键是确定两人数量比,掌握按比例分配问题的解题方法。
15.×
【分析】分子大于或等于分母的分数叫做假分数;乘积是1的两个数互为倒数,据此举例解答。
【详解】如假分数,的倒数是;<;
如假分数,的倒数是;=。
所以假分数的倒数小于或等于原数。
原题干说法错误。
故答案为:×
16.×
【分析】根据题意可得:1箱苹果的重量-1箱橘子的重量=5千克,等式两边同时乘5即可判断正误。
【详解】由分析可知: 1箱苹果比1箱橘子重5千克,那么5箱苹果比5箱橘子重25千克,原题说法错误。
故答案为:×。
【点睛】本题主要考查等量关系,清楚的知道苹果和橘子的关系是解题条件。
17.×
【分析】,先算乘法,再算减法,据此进行计算。
【详解】,原题计算顺序和结果错误。
故答案为:×
18.√
【分析】一个正方体有12条相等的棱和8个顶点,据此判断即可。
【详解】搭一个正方体需要12根长短相等的小棒作为正方体的12条相等的棱,8个橡皮泥小球作为8个顶点,说法正确。
故答案为:√
19.√
【分析】任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫作圆周率,用字母π表示。据此解答。
【详解】由分析知:任意一个圆,其周长和直径的比值都等于圆周率,圆周率不随圆的大小的改变而改变。
所以圆无论大小,它的周长与直径的比值都相等,说法正确。
故答案为:√
20.4.3;1.4;2.3;12.56
;;;
【详解】略
21.;3;
【分析】(1)先算括号里面的除法,再根据减法的性质a-(b+c)=a-b-c进行简算;
(2)根据加法交换律a+b=b+a,加法结合律(a+b)+c=a+(b+c)进行简算;
(3)先算小括号里面的加法,再算中括号里面的乘法,最后算中括号外面的除法。
【详解】(1)
(2)
(3)
22.;;
【分析】,根据等式的性质1和2,两边同时-,再同时÷即可;
,先将左边合并成,根据等式的性质2,两边同时÷即可;
,根据等式的性质2,两边同时×,再同时÷2即可。
【详解】
解:
解:
解:
23.248平方分米
【分析】表面积是指物体外表面积,通常是指物体表面的总面积。上面的两个小长方形和凹进去的长方形合在一起恰好就是一个长方体的表面积。则表面积=长方体的表面积+4个长方形的面积+4个小正方形的面积。长方体的表面积=(长×宽+长×高+宽×高)×2,小长方形的长是6分米,宽是2分米,面积=长×宽。正方形的边长是2分米,面积=边长×边长。
【详解】
=
=
=(平方分米)
(平方分米)
(平方分米)
(平方分米)
则图形的表面积是248平方分米。
24.48人;2人
【分析】由题意可知,人的数量必须是整数,全班人数必须能同时被6和8整除,且小于50,可找出6和8的50以内的公倍数有:24、48,所以这个数最大为,这个班最多有48人。把全班人数看作单位“1”,再根据求一个数的几分之几是多少,用乘法计算,可分别求出参加田径队和参加篮球队的人数,最后再相减可得参加田径队的比参加篮球队多的人数。
【详解】6和8的50以内的公倍数有:24、48。
这个班最多有:(人)
(人)
(人)
(人)
答:这个班最多有48人;参加田径队的比参加篮球队的多2人。
25.垃圾桶4个;文件框10个
【分析】设买x个垃圾桶,买的文件框比垃圾桶多6个,则文件框(x+6)个,每个垃圾桶20元,x个是20x元,每个文件框是10元,(x+6)个文件框是(x+6)×10元;买垃圾桶的钱数+买文件框的钱数=180元;列方程:20x+(x+6)×10=180,解方程,即可解答。
【详解】解:设买x个垃圾桶,则买文件框(x+6)个。
20x+(x+6)×10=180
20x+10x+6×10=180
30x=180-60
30x=120
x=120÷30
x=4
文件框:4+6=10(个)
答:王阿姨买了4个垃圾桶,10个文件框。
【点睛】本题考查鸡兔同笼的问题,根据题意,设出未知数,利用买垃圾桶和文件框的价钱列方程,解方程。
26.黄沙:10.8吨;石子21.6吨
【分析】把水泥、黄沙、石子的总重量看作单位“1”,水泥、黄沙、石子按1∶2∶4拌成,即水泥占水泥、黄沙、石子的总重量的,对应的是水泥的重量,求单位“1”,用水泥的重量÷,求出水泥、黄沙、石子的总重量,黄沙占水泥、黄沙、石子的总重量,用水泥、黄沙、石子的总重量×,求出运来黄沙的重量;石子占水泥、黄沙、石子的总重量的,用水泥、黄沙、石子的总重量×,即可求出运来石子的重量。
【详解】5.4÷
=5.4÷
=5.4×7
=37.8(吨)
37.8×
=37.8×
=10.8(吨)
37.8×
=37.8×
=21.6(吨)
答:应再运来黄沙10.8吨和21.6吨石子才能正好拌成这种混凝土。
27.1960辆
【分析】把计划的生产数量看成单位“1”,全年实际一共完成了计划的(+),用乘法求出实际一共完成了多少辆,然后再用实际完成的数量减去计划的数量就是超产完成了多少辆。
【详解】12600×(+)﹣12600
=12600×﹣12600
=14560﹣12600
=1960(辆)
答:全年超产1960辆。
【点睛】此题考查的是分数应用题的列式,要先找准单位“1”,再据题中的数量关系列式求解。
28.29.5千克
【分析】粉刷面积=长×宽+长×高×2+宽×高×2-门窗面积,粉刷面积×每平方米用的涂料质量=需要的涂料总质量,据此列式解答。
【详解】8×6+8×3×2+6×3×2-14
=48+48+36-14
=118(平方米)
118×0.25=29.5(千克)
答:共需要涂料29.5千克。
29.6750毫升
【分析】根据题意,裁剪一块长方形铁皮焊接成一个底面是正方形的无盖长方体,则少上面,共有5个面,且底面是正方形,4个侧面完全相同。
从图中可知,把长方形的长边平均分成两半,这样左右两边都是边长为30厘米的正方形,左边的正方形作为长方体的底面,根据正方形的面积=边长×边长,求出长方体的底面积;
把右边的正方形再平均分成4个小长方形,这4个小长方形作为长方体的侧面,用30÷4即可求出长方体的高;
最后根据公式V=Sh,以及进率:1立方厘米=1毫升,求出这个无盖长方体容器的容积。
【详解】正方形的边长:60÷2=30(厘米)
长方体的高:30÷4=7.5(厘米)
长方体的体积:
30×30×7.5
=900×7.5
=6750(立方厘米)
6750立方厘米=6750毫升
答:这个长方体容器的容积是6750毫升。
【点睛】本题考查长方体体积(容积)公式的灵活运用,找出长方体容器的底面积和高是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1-5单元阶段测试卷-数学六年级上册苏教版
一、选择题
1.现有190张铁皮做盒子,每张铁皮做8个盒身或做22个盒底,而1个盒身与2个盒底配成1个盒子,则用( )张铁皮做盒身。
A.80 B.100 C.110 D.90
2.一根3米长的绳子,第一次用去,第二次用去米,两次用去的长度相比,( )。
A.第一次长 B.第二次长 C.一样长 D.无法比较
3.文具里有蓝、黄两种铅笔出售,蓝铅笔3元4支,黄铅笔4元3支,蓝、黄两种铅笔的单价比是( )。
A.16∶9 B.9∶16 C.1∶1 D.无法比较
4.如果7-(÷□+)=5,那么□=( )。
A. B. C. D.
5.如图所示,明明在一个长方体玻璃容器中摆了若干个体积为1立方厘米的小正方体。由此可知,这个玻璃容器的容积是( )立方厘米。
A.72 B.84 C.90 D.95
6.一个正方体的表面积是24cm2,如果底面不变,高度增加3cm,体积增加( )cm3。
A.4 B.24 C.56 D.12
二、填空题
7.一台电视机降价,是把( )看作单位“1”。如果原价是3600元,那么现在降价了( )元,现价是( )元。
8.5个大盒和2个小盒共装了240个球,每个大盒比每个小盒多装20个。每个大盒装( )个球,每个小盒装( )个球。
9.妈妈买来猕猴桃和柠檬共60个,其中猕猴桃占,吃去( )个柠檬后,猕猴桃与柠檬的个数比是4∶5。
10.如图是用棱长1厘米的正方体木块摆成的几何体,它的体积是( )立方厘米,表面积是( )平方厘米。
11.一个分数与它本身相加、相减、相除,把所得的和、差、商相加,结果是,这个分数是。
12.明明要围一个棱长5分米的正方体框架,他至少要准备一根( )分米长的铁丝。
13.春节前夕,小红用一根长120厘米的铁丝做一个长方体灯笼的框架,他的长、宽、高的比是2∶1∶3,在这个灯笼框架的侧面糊上彩纸,彩纸的面积至少是( )平方厘米。这个灯笼的框架的体积是( )立方厘米。
14.小明和小刚共收集121张卡片,已知小明卡片数量的和小刚卡片数量的相等。小明收集了( )张卡片,小刚收集了( )张卡片。
三、判断题
15.假分数的倒数都比原数大。( )
16.1箱苹果比1箱橘子重5千克,那么5箱苹果比5箱橘子重5千克。( )
17.。( )
18.搭一个正方体需要12根长短相等的小棒和8个橡皮泥小球。( )
19.无论大小,圆的周长与直径的比值都相等。( )
四、计算题
20.直接写出得数。
3.5+0.8= 3-1.6= 0.23÷0.1= 3.14×4=
21.计算下面各题。(能简算的要用简便方法算)
22.解方程。
23.计算下图的表面积。(单位:分米)
五、解答题
24.六年级一班的人数不足50人,参加田径队的人数占全班人数的,参加篮球队的人数占全班人数的。这个班最多有多少人?参加田径队的比参加篮球队的多几人?
25.“五一”节活动期间,王阿姨在京东自营店为公司买了垃圾桶和文件框共花了180元,每个垃圾桶20元,每个文件框10元,买的文件框比垃圾桶多6个。王阿姨买了垃圾桶和文件框分别多少个?
26.一种混凝土是将水泥、黄沙、石子按1∶2∶4拌成的,现有水泥5.4吨,应再运来多少吨黄沙和石子才能正好拌成这种混凝土?
27.某汽车厂去年计划生产汽车12600辆,结果上半年完成了全年计划的,下半年完成全年计划的。全年超产汽车多少辆?
28.一间长方体形状的教室,长8米,宽6米,高3米,门窗面积共14平方米。要粉刷教室的四壁和天花板,如果每平方米用涂料0.25千克,共需要涂料多少千克?
29.王大伯按照下图裁剪一块长方形铁皮,焊接成一个底面是正方形的无盖长方体。这个长方体容器的容积是多少毫升?
参考答案:
题号 1 2 3 4 5 6
答案 C A B B A D
1.C
【分析】先设x张铁皮做盒身,则(190-x)张铁皮做盒底。根据题意可知,一个盒身需要两个盒底,每张铁皮做8个盒身或做22个盒底,所以得出方程式为:2×8x=22(190-x),解出x即可。
【详解】解:设x张铁皮做盒身,则(190-x)张铁皮做盒底。
2×8x=22(190-x)
16x=4180-22x
16x+22x=4180-22x+22x
38x=4180
38x÷38=4180÷38
x=110
用110张铁皮做盒身。
故答案为:C
2.A
【分析】把绳子的长度看作单位“1”,第一次用去,用绳子的长度×,求出第一次用去的长度,再和第二次用去的长度进行比较,即可解答。
【详解】3×=1(米)
1>,第一次长。
一根3米长的绳子,第一次用去,第二次用去米,两次用去的长度相比,第一次长。
故答案为:A
3.B
【分析】根据总价÷数量=单价,据此分别求出蓝铅笔和黄铅笔的单价,再写出它们的单价比,最后化简为最简整数比。
【详解】蓝铅笔的单价:3÷4=(元)
黄铅笔的单价:4÷3=(元)
蓝铅笔的单价与黄铅笔的单价比:
∶
=(×12)∶(×12)
=9∶16
故答案为:B
4.B
【分析】7-(÷□+)=5根据题目可知,7减去括号里的数等于5,则括号里的数是:7-5=2,即÷□+=2,把□可以当成一个x,即÷x+=2,根据等式的性质1和等式的性质2解出x的值即□的值。
【详解】由分析可知,把□看成x
即原式变为:7-(÷x+)=5
解:÷x+=7-5
÷x+=2
÷x=2-
÷x=
x=÷
x=
故答案为:B。
【点睛】本题主要考查解方程,熟练掌握等式的性质1和等式的性质2,并灵活运用。
5.A
【分析】根据正方体的体积公式V=a3,可知体积为1立方厘米的小正方体的棱长是1厘米。
观察图形可知,长方体玻璃容器的长、宽、高分别摆有6个、4个、3个小正方体,所以它的长是6厘米,宽是4厘米,高是3厘米;根据长方体的体积(容积)公式V=abh,即可求出这个玻璃容器的容积。
【详解】因为1=1×1×1,所以体积为1立方厘米的小正方体的棱长是1厘米。
6×4×3
=24×3
=72(立方厘米)
这个玻璃容器的容积是72立方厘米。
故答案为:A
6.D
【分析】根据正方体的表面积公式S=6a2,可得出正方体的底面积,如果底面不变,高度增加3cm,增加的体积=正方体底面积×增加的高,据此作答。
【详解】24÷6×3
=4×3
=12(cm3)
故答案为:D
【点睛】本题考查正方体表面积和长方体体积公式的灵活运用,关键是求出正方体的底面积。
7. 原价 1600 2000
【分析】由题意可知,把原价看作单位“1”,根据求一个数的几分之几是多少,用乘法计算,用原价乘,得到降价的钱数,再用原价减降价的钱数,可得现价。
【详解】(元)
(元)
一台电视机降价,是把原价看作单位“1”。如果原价是3600元,那么现在降价了1600元,现价是2000元。
8. 40 20
【分析】240个球再增加2×20=40个球,就是7个大盒共装求的个数(240+40=280个),由此得出每个大盒装280÷7=40个球,进而可得每个小盒装40-20=20个球;据此解答。
【详解】(240+20×2)÷(5+2)
=280÷7
=40(个)
40-20=20(个)
【点睛】理解“240个球再增加2×20=40个球,就是7个大盒共装求的个数(240+40=280个)”是解题的关键。
9.6
【分析】已知猕猴桃和柠檬共60个,其中猕猴桃占,根据求一个数的几分之几是多少,用猕猴桃和柠檬的总数乘,求出猕猴桃的个数;再用总数减去猕猴桃的个数,即是柠檬原有的个数;已知吃去若干个柠檬后,猕猴桃与柠檬的个数比是4∶5,即柠檬剩下的个数占猕猴桃的,把猕猴桃的个数看作单位“1”,单位“1”已知,用猕猴桃的个数乘,求出柠檬剩下的个数;最后用柠檬原有的个数减去剩下的个数,即是吃掉柠檬的个数。
【详解】猕猴桃:60×=24(个)
原有柠檬:60-24=36(个)
吃去几个柠檬后还剩下的柠檬:
24×=30(个)
吃去的柠檬:36-30=6(个)
所以,吃去6个柠檬后,猕猴桃与柠檬的个数比是4∶5。
10. 15 46
【分析】根据正方体的体积公式V=a3,可知棱长1厘米的正方体的体积是1立方厘米;从图中数出正方体的个数,再乘用正方体的体积,即是这个几何体的体积。
已知正方体的棱长是1厘米,那么正方体一个面的面积是1平方厘米。求这个几何体的表面积,就是求露出正方体的面的面积之和,分别数出从上下面、前后面、左右面看到的小正方形的个数,再乘一个面的面积即可。
【详解】1×1×1×15=15(立方厘米)
(9+7+7)×2
=23×2
=46(个)
1×1×46=46(平方厘米)
它的体积是15立方厘米,表面积是46平方厘米。
11.
【分析】一个数+它本身=这个数的2倍,一个数-它本身=0,一个数÷它本身=1,据此用(和、差、商相加的结果-1)=这个分数的2倍,再除以2就是这个分数。
【详解】(-1)÷2
=÷2
=×
=
这个分数是。
【点睛】关键是明确特殊的加、减和除法的结果,掌握分数除法的计算方法。
12.60
【分析】根据题意,用一根铁丝围成一个正方体框架,那么铁丝的长度等于正方体的棱长总和;根据正方体的棱长总和=棱长×12,代入数据计算,求出铁丝的长度。
【详解】5×12=60(分米)
他至少要准备一根60分米长的铁丝。
13. 450 750
【分析】根据按比例分配,先求出小红做的长方体灯笼的长、宽、高的长度;侧面糊上彩纸,就是长方体表面积去掉上下两个面,根据表面积公式:(宽×高+长×高)×2,代入数据,求出侧面积;再根据长方体的体积公式:长×宽×高,代入数据,即可解答。
【详解】长:120÷4×
=30×
=10(厘米)
宽:120÷4×
=30×
=5(厘米)
高:120÷4×
=30×
=15(厘米)
侧面积:(5×15+10×15)×2
=(75+150)×2
=225×2
=450(平方厘米)
体积:10×5×15
=50×15
=750(立方厘米)
【点睛】本题考查长方体的特征,长方体表面积公式、体积公式的应用;以及按比例分配问题。
14. 55 66
【分析】先确定两人卡片数量比,总数量÷总份数,求出一份数,一份数分别乘两人对应份数即可。
【详解】小明卡片数量×=小刚卡片数量×
小明卡片数量∶小刚卡片数量=5∶6
121÷(5+6)
=121÷11
=11(张)
11×5=55(张)
11×6=66(张)
【点睛】关键是确定两人数量比,掌握按比例分配问题的解题方法。
15.×
【分析】分子大于或等于分母的分数叫做假分数;乘积是1的两个数互为倒数,据此举例解答。
【详解】如假分数,的倒数是;<;
如假分数,的倒数是;=。
所以假分数的倒数小于或等于原数。
原题干说法错误。
故答案为:×
16.×
【分析】根据题意可得:1箱苹果的重量-1箱橘子的重量=5千克,等式两边同时乘5即可判断正误。
【详解】由分析可知: 1箱苹果比1箱橘子重5千克,那么5箱苹果比5箱橘子重25千克,原题说法错误。
故答案为:×。
【点睛】本题主要考查等量关系,清楚的知道苹果和橘子的关系是解题条件。
17.×
【分析】,先算乘法,再算减法,据此进行计算。
【详解】,原题计算顺序和结果错误。
故答案为:×
18.√
【分析】一个正方体有12条相等的棱和8个顶点,据此判断即可。
【详解】搭一个正方体需要12根长短相等的小棒作为正方体的12条相等的棱,8个橡皮泥小球作为8个顶点,说法正确。
故答案为:√
19.√
【分析】任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫作圆周率,用字母π表示。据此解答。
【详解】由分析知:任意一个圆,其周长和直径的比值都等于圆周率,圆周率不随圆的大小的改变而改变。
所以圆无论大小,它的周长与直径的比值都相等,说法正确。
故答案为:√
20.4.3;1.4;2.3;12.56
;;;
【详解】略
21.;3;
【分析】(1)先算括号里面的除法,再根据减法的性质a-(b+c)=a-b-c进行简算;
(2)根据加法交换律a+b=b+a,加法结合律(a+b)+c=a+(b+c)进行简算;
(3)先算小括号里面的加法,再算中括号里面的乘法,最后算中括号外面的除法。
【详解】(1)
(2)
(3)
22.;;
【分析】,根据等式的性质1和2,两边同时-,再同时÷即可;
,先将左边合并成,根据等式的性质2,两边同时÷即可;
,根据等式的性质2,两边同时×,再同时÷2即可。
【详解】
解:
解:
解:
23.248平方分米
【分析】表面积是指物体外表面积,通常是指物体表面的总面积。上面的两个小长方形和凹进去的长方形合在一起恰好就是一个长方体的表面积。则表面积=长方体的表面积+4个长方形的面积+4个小正方形的面积。长方体的表面积=(长×宽+长×高+宽×高)×2,小长方形的长是6分米,宽是2分米,面积=长×宽。正方形的边长是2分米,面积=边长×边长。
【详解】
=
=
=(平方分米)
(平方分米)
(平方分米)
(平方分米)
则图形的表面积是248平方分米。
24.48人;2人
【分析】由题意可知,人的数量必须是整数,全班人数必须能同时被6和8整除,且小于50,可找出6和8的50以内的公倍数有:24、48,所以这个数最大为,这个班最多有48人。把全班人数看作单位“1”,再根据求一个数的几分之几是多少,用乘法计算,可分别求出参加田径队和参加篮球队的人数,最后再相减可得参加田径队的比参加篮球队多的人数。
【详解】6和8的50以内的公倍数有:24、48。
这个班最多有:(人)
(人)
(人)
(人)
答:这个班最多有48人;参加田径队的比参加篮球队的多2人。
25.垃圾桶4个;文件框10个
【分析】设买x个垃圾桶,买的文件框比垃圾桶多6个,则文件框(x+6)个,每个垃圾桶20元,x个是20x元,每个文件框是10元,(x+6)个文件框是(x+6)×10元;买垃圾桶的钱数+买文件框的钱数=180元;列方程:20x+(x+6)×10=180,解方程,即可解答。
【详解】解:设买x个垃圾桶,则买文件框(x+6)个。
20x+(x+6)×10=180
20x+10x+6×10=180
30x=180-60
30x=120
x=120÷30
x=4
文件框:4+6=10(个)
答:王阿姨买了4个垃圾桶,10个文件框。
【点睛】本题考查鸡兔同笼的问题,根据题意,设出未知数,利用买垃圾桶和文件框的价钱列方程,解方程。
26.黄沙:10.8吨;石子21.6吨
【分析】把水泥、黄沙、石子的总重量看作单位“1”,水泥、黄沙、石子按1∶2∶4拌成,即水泥占水泥、黄沙、石子的总重量的,对应的是水泥的重量,求单位“1”,用水泥的重量÷,求出水泥、黄沙、石子的总重量,黄沙占水泥、黄沙、石子的总重量,用水泥、黄沙、石子的总重量×,求出运来黄沙的重量;石子占水泥、黄沙、石子的总重量的,用水泥、黄沙、石子的总重量×,即可求出运来石子的重量。
【详解】5.4÷
=5.4÷
=5.4×7
=37.8(吨)
37.8×
=37.8×
=10.8(吨)
37.8×
=37.8×
=21.6(吨)
答:应再运来黄沙10.8吨和21.6吨石子才能正好拌成这种混凝土。
27.1960辆
【分析】把计划的生产数量看成单位“1”,全年实际一共完成了计划的(+),用乘法求出实际一共完成了多少辆,然后再用实际完成的数量减去计划的数量就是超产完成了多少辆。
【详解】12600×(+)﹣12600
=12600×﹣12600
=14560﹣12600
=1960(辆)
答:全年超产1960辆。
【点睛】此题考查的是分数应用题的列式,要先找准单位“1”,再据题中的数量关系列式求解。
28.29.5千克
【分析】粉刷面积=长×宽+长×高×2+宽×高×2-门窗面积,粉刷面积×每平方米用的涂料质量=需要的涂料总质量,据此列式解答。
【详解】8×6+8×3×2+6×3×2-14
=48+48+36-14
=118(平方米)
118×0.25=29.5(千克)
答:共需要涂料29.5千克。
29.6750毫升
【分析】根据题意,裁剪一块长方形铁皮焊接成一个底面是正方形的无盖长方体,则少上面,共有5个面,且底面是正方形,4个侧面完全相同。
从图中可知,把长方形的长边平均分成两半,这样左右两边都是边长为30厘米的正方形,左边的正方形作为长方体的底面,根据正方形的面积=边长×边长,求出长方体的底面积;
把右边的正方形再平均分成4个小长方形,这4个小长方形作为长方体的侧面,用30÷4即可求出长方体的高;
最后根据公式V=Sh,以及进率:1立方厘米=1毫升,求出这个无盖长方体容器的容积。
【详解】正方形的边长:60÷2=30(厘米)
长方体的高:30÷4=7.5(厘米)
长方体的体积:
30×30×7.5
=900×7.5
=6750(立方厘米)
6750立方厘米=6750毫升
答:这个长方体容器的容积是6750毫升。
【点睛】本题考查长方体体积(容积)公式的灵活运用,找出长方体容器的底面积和高是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
