2024-2025学年江苏省盐城市鹿鸣路初级中学八年级(上)期中考试数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年江苏省盐城市鹿鸣路初级中学八年级(上)期中考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 682.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 19:32:08 | ||
图片预览




文档简介
2024-2025学年江苏省盐城市鹿鸣路初级中学八年级(上)期中考试
数学试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.第届夏季奥运会将于年月日至月日在法国巴黎举行,如图所示巴黎奥运会项目图标中,轴对称图形是( )
A. B. C. D.
2.一个等腰三角形的两条边分别为和,则第三条边的长等于( )
A. B. C. 或 D.
3.在平面直角坐标系中,点所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4.下列四个数中,无理数是( )
A. B. C. D.
5.下列四组线段中,可以构成直角三角形的是( )
A. ,, B. ,, C. ,, D. ,,
6.点向上平移个单位,则所得到的点的坐标为( )
A. B. C. D.
7.汽车开始行驶时,油箱内有油升,如果每小时耗油升,则油箱内剩余油量升与行驶时间时的关系式为( )
A. B.
C. D.
8.如图,在象棋棋盘上建立平面直角坐标系,使“马”位于点,“兵”位于点,则“帅”所在位置的坐标是( )
A. B. C. D.
二、填空题:本题共8小题,每小题3分,共24分。
9.的算术平方根是 .
10.等腰三角形的底角等于度,则它的顶角是 度。
11.函数中,自变量的取值范围是 .
12.用四舍五入法取近似数, 精确到百分位.
13.比较大小: .
14.已知点,则点到轴的距离是 .
15.如图,射线是的角平分线,是射线上一点,于点,,若点是射线上一点,,则的面积是
16.第二十四届国际数学家大会会徽的设计基础是多年前中国古代数学家赵爽的“弦图”如图,在由四个全等的直角三角形和中间一个小正方形拼成的大正方形中,连接、若的面积是的倍,小正方形的面积是,则大正方形的面积 .
三、计算题:本大题共2小题,共12分。
17.解方程:
;
.
18.计算:
四、解答题:本题共8小题,共64分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
已知的平方根是,的立方根是,求的立方根.
20.本小题分
如图,点、、在一条直线上,、均为等边三角形.求证:.
21.本小题分
如图,在平面直角坐标系中,如图所示.
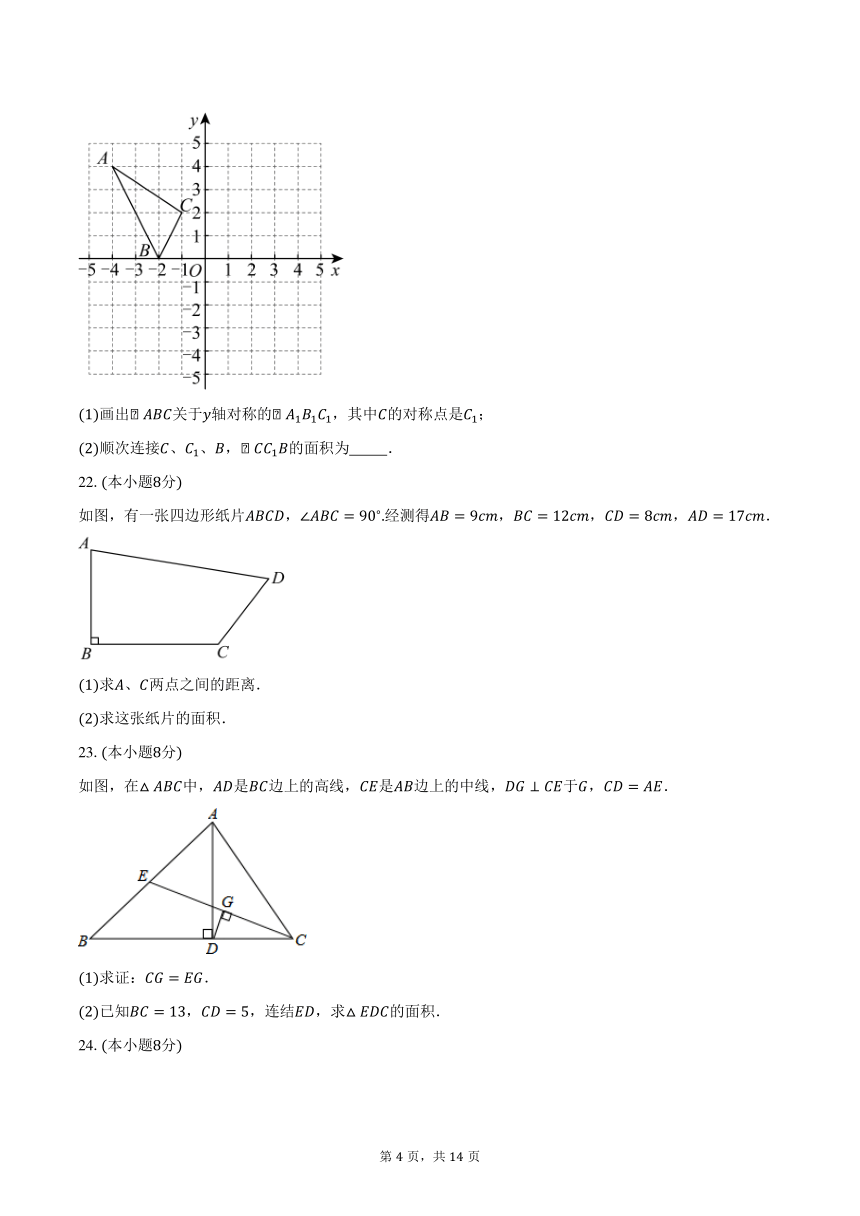
画出关于轴对称的,其中的对称点是;
顺次连接、、,的面积为 .
22.本小题分
如图,有一张四边形纸片,经测得,,,.
求、两点之间的距离.
求这张纸片的面积.
23.本小题分
如图,在中,是边上的高线,是边上的中线,于,.
求证:.
已知,,连结,求的面积.
24.本小题分
如果正整数、、满足等式,那么正整数、、叫做勾股数.小明根据自己探究勾股数的过程,列成下表:
小明发现:,,,请你根据小明发现的规律写出下一组勾股数: ;
若用为整数,且表示,那么、用含的代数式分别表示为__________和_____,请用所学知识说明它们是一组勾股数.
25.本小题分
在平面直角坐标系中,直线为经过且垂直于轴的直线,图形关于轴的对称图形称为图形的一次对称图形,记作图形,图形关于直线的对称图形称为图形的二次对称图形,记作图形.
例如,点的一次对称点为,二次对称点为根据定义,回答下列问题:
点的一次对称点为 ,二次对称点为 .当点在第三象限时,点、,中可以是点的二次对称点的是 ;
若点在第三象限,点、分别是点的一次对称点、二次对称点,若为等腰直角三角形,则、应满足关系式: ;
已知点,若以为边的正方形、在线段的上方的二次对称图形与过且垂直于轴的直线有公共点,求的取值范围.
26.本小题分
【概念认知】
在凸四边形中内角度数都小于,若其中有三个顶点构成的三角形是等腰直角三角形,则称该四边形为直等腰四边形.
【理解应用】
如图,如图所示,请用无刻度的直尺和圆规作出点只需作出一个即可,使、、、四个点构成的四边形是直等腰四边形;
如图,在中,,,,点是边上的一个动点不与、重合,将沿着翻折得到,当、、、四个点构成的四边形是直等腰四边形时,求的长;
【拓展提升】
如图,在直等腰四边形中,,,为等腰直角三角形,且,若,则的长为 直接写出答案.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.【小题】
解:
,
解得或;
【小题】
解:,
,
.
18.解:
19.解:的平方根是,的立方根是,
, ,
,
,
的立方根是,
的立方根是.
20.证明:、均为等边三角形,
,,,
,
即,
在和中
,
.
21.【小题】
解:如图所示,即为所求;
【小题】
22.【小题】
解:连结.
在中,,,,
.
即、两点之间的距离为.
【小题】
解:,
,
,
是直角三角形且,
四边形纸片的面积
.
23.【小题】
证明:连接,
是边上的中线
是的中点
又
即是等腰三角形,
,
;
【小题】
如图,过点作于点,
,
,
,
为等腰三角形,
又,
在中,
24.【小题】
,,
【小题】
解:,
,,
,,,
,
,,是一组勾股数.
故答案为:,
25.【小题】
【小题】
【小题】
解:点,,且四边形是以为边的、在线段的上方的正方形,
,,
正方形的二次对称图形的各顶点为,,,,
二次对称图形与过且垂直于轴的直线有公共点,
若点,在该直线上,则
,解得,
若点,在该直线上,则
,解得,
的取值范围是.
26.【小题】
解:如图所示:以、为圆心,大于为半径作弧,交于点,,作直线交于点,以为圆心,为半径作弧交于,四边形即为所求.
由作法可知:直线为线段的垂直平分线,点在直线上,
,,
,
,
,
,即,
四边形为直等腰四边形;
;
【小题】
Ⅰ当点在下方时,
、、、四个点构成的四边形是直等腰四边形,
为等腰直角三角形,
,
,,
,
沿着翻折得到,
,,
即,
作于点,
,,
为等腰直角三角形,
在中,,
,,
在中,,
,;
Ⅱ当点在上方时,如图所示:
、、、四个点构成的四边形是直等腰四边形,
为等腰直角三角形,
,
,,
,
沿着翻折得到,
,
,
,
作于点,
,,
为等腰直角三角形,
在中,,
,,
在中,,
,;
综上所述,的长为或;
【小题】
第1页,共1页
数学试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.第届夏季奥运会将于年月日至月日在法国巴黎举行,如图所示巴黎奥运会项目图标中,轴对称图形是( )
A. B. C. D.
2.一个等腰三角形的两条边分别为和,则第三条边的长等于( )
A. B. C. 或 D.
3.在平面直角坐标系中,点所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4.下列四个数中,无理数是( )
A. B. C. D.
5.下列四组线段中,可以构成直角三角形的是( )
A. ,, B. ,, C. ,, D. ,,
6.点向上平移个单位,则所得到的点的坐标为( )
A. B. C. D.
7.汽车开始行驶时,油箱内有油升,如果每小时耗油升,则油箱内剩余油量升与行驶时间时的关系式为( )
A. B.
C. D.
8.如图,在象棋棋盘上建立平面直角坐标系,使“马”位于点,“兵”位于点,则“帅”所在位置的坐标是( )
A. B. C. D.
二、填空题:本题共8小题,每小题3分,共24分。
9.的算术平方根是 .
10.等腰三角形的底角等于度,则它的顶角是 度。
11.函数中,自变量的取值范围是 .
12.用四舍五入法取近似数, 精确到百分位.
13.比较大小: .
14.已知点,则点到轴的距离是 .
15.如图,射线是的角平分线,是射线上一点,于点,,若点是射线上一点,,则的面积是
16.第二十四届国际数学家大会会徽的设计基础是多年前中国古代数学家赵爽的“弦图”如图,在由四个全等的直角三角形和中间一个小正方形拼成的大正方形中,连接、若的面积是的倍,小正方形的面积是,则大正方形的面积 .
三、计算题:本大题共2小题,共12分。
17.解方程:
;
.
18.计算:
四、解答题:本题共8小题,共64分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
已知的平方根是,的立方根是,求的立方根.
20.本小题分
如图,点、、在一条直线上,、均为等边三角形.求证:.
21.本小题分
如图,在平面直角坐标系中,如图所示.
画出关于轴对称的,其中的对称点是;
顺次连接、、,的面积为 .
22.本小题分
如图,有一张四边形纸片,经测得,,,.
求、两点之间的距离.
求这张纸片的面积.
23.本小题分
如图,在中,是边上的高线,是边上的中线,于,.
求证:.
已知,,连结,求的面积.
24.本小题分
如果正整数、、满足等式,那么正整数、、叫做勾股数.小明根据自己探究勾股数的过程,列成下表:
小明发现:,,,请你根据小明发现的规律写出下一组勾股数: ;
若用为整数,且表示,那么、用含的代数式分别表示为__________和_____,请用所学知识说明它们是一组勾股数.
25.本小题分
在平面直角坐标系中,直线为经过且垂直于轴的直线,图形关于轴的对称图形称为图形的一次对称图形,记作图形,图形关于直线的对称图形称为图形的二次对称图形,记作图形.
例如,点的一次对称点为,二次对称点为根据定义,回答下列问题:
点的一次对称点为 ,二次对称点为 .当点在第三象限时,点、,中可以是点的二次对称点的是 ;
若点在第三象限,点、分别是点的一次对称点、二次对称点,若为等腰直角三角形,则、应满足关系式: ;
已知点,若以为边的正方形、在线段的上方的二次对称图形与过且垂直于轴的直线有公共点,求的取值范围.
26.本小题分
【概念认知】
在凸四边形中内角度数都小于,若其中有三个顶点构成的三角形是等腰直角三角形,则称该四边形为直等腰四边形.
【理解应用】
如图,如图所示,请用无刻度的直尺和圆规作出点只需作出一个即可,使、、、四个点构成的四边形是直等腰四边形;
如图,在中,,,,点是边上的一个动点不与、重合,将沿着翻折得到,当、、、四个点构成的四边形是直等腰四边形时,求的长;
【拓展提升】
如图,在直等腰四边形中,,,为等腰直角三角形,且,若,则的长为 直接写出答案.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.【小题】
解:
,
解得或;
【小题】
解:,
,
.
18.解:
19.解:的平方根是,的立方根是,
, ,
,
,
的立方根是,
的立方根是.
20.证明:、均为等边三角形,
,,,
,
即,
在和中
,
.
21.【小题】
解:如图所示,即为所求;
【小题】
22.【小题】
解:连结.
在中,,,,
.
即、两点之间的距离为.
【小题】
解:,
,
,
是直角三角形且,
四边形纸片的面积
.
23.【小题】
证明:连接,
是边上的中线
是的中点
又
即是等腰三角形,
,
;
【小题】
如图,过点作于点,
,
,
,
为等腰三角形,
又,
在中,
24.【小题】
,,
【小题】
解:,
,,
,,,
,
,,是一组勾股数.
故答案为:,
25.【小题】
【小题】
【小题】
解:点,,且四边形是以为边的、在线段的上方的正方形,
,,
正方形的二次对称图形的各顶点为,,,,
二次对称图形与过且垂直于轴的直线有公共点,
若点,在该直线上,则
,解得,
若点,在该直线上,则
,解得,
的取值范围是.
26.【小题】
解:如图所示:以、为圆心,大于为半径作弧,交于点,,作直线交于点,以为圆心,为半径作弧交于,四边形即为所求.
由作法可知:直线为线段的垂直平分线,点在直线上,
,,
,
,
,
,即,
四边形为直等腰四边形;
;
【小题】
Ⅰ当点在下方时,
、、、四个点构成的四边形是直等腰四边形,
为等腰直角三角形,
,
,,
,
沿着翻折得到,
,,
即,
作于点,
,,
为等腰直角三角形,
在中,,
,,
在中,,
,;
Ⅱ当点在上方时,如图所示:
、、、四个点构成的四边形是直等腰四边形,
为等腰直角三角形,
,
,,
,
沿着翻折得到,
,
,
,
作于点,
,,
为等腰直角三角形,
在中,,
,,
在中,,
,;
综上所述,的长为或;
【小题】
第1页,共1页
同课章节目录
