北京市第五十七中学2024~2025学年第一学期12月数学月考试卷(PDF版,无答案)
文档属性
| 名称 | 北京市第五十七中学2024~2025学年第一学期12月数学月考试卷(PDF版,无答案) |

|
|
| 格式 | |||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 00:00:00 | ||
图片预览

文档简介
北京市第五十七中学初三 12 月数学练习
班级: 姓名: 2024.12
一、选择题(本题共 30 分,每小题 3 分)
1. 函数 y (x 1)2 2的最小值是
A.1 B.-1 C.2 D.-2
2. 2点 A( 1,y1), B(1,y2),C(2,y3)是反比例函数 y 图象上的三个点,则 y1 ,y2 ,y3 的x
大小关系是
A. y3 y2 y1 B. y1 y3 y2 C. y2 y3 y1 D. y3 y1 y2
3.方程 x2 - x + 3 = 0的根的情况是
A.有两个不相等的实数根 B.有两个相等的实数根
C.无实数根 D.只有一个实数根
4 2.如图,在平面直角坐标系 xOy中,B是反比例函数 y = (x > 0)的图象上的
x
一点,则矩形 OABC的面积为
A.1 B. 2
C.3 D. 4
5.如图,将△ABC绕点 A逆时针旋转 100°,得到△ADE.若点 D在线段
BC的延长线上,则 B的大小为
A.30° B.40°
C.50° D.60°
6.一个扇形的圆心角是 120°,面积为 3πcm2,那么这个扇形的半径是
A. 1cm B. 3cm C. 6cm D. 9cm
k
7.如图,反比例函数 y 的图象经过点 A(4,1),当 y 1时,x的取值
x
范围是
A. x 0或 x 4 B. 0 x 4
C. x 4 D. x 4
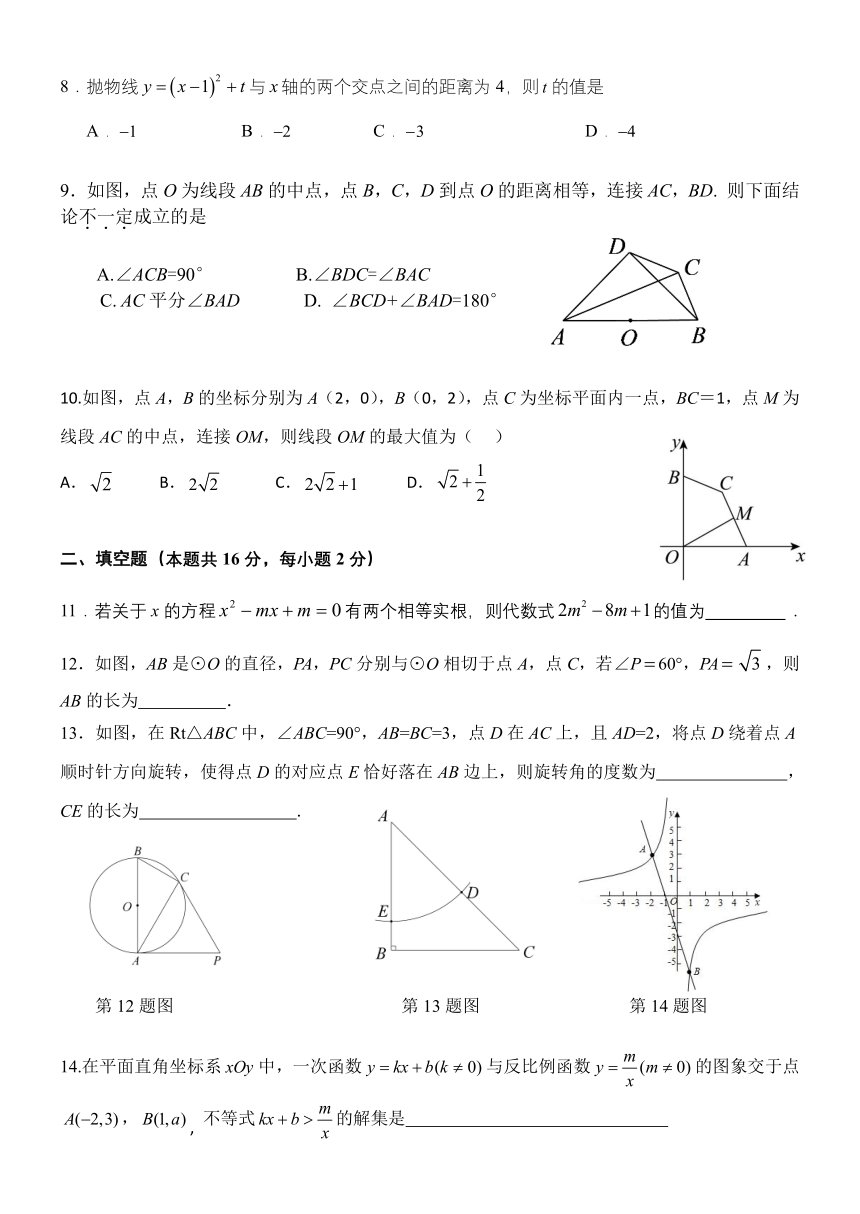
8.抛物线 y x 1 2 t与 x轴的两个交点之间的距离为 4,则 t 的值是
A. 1 B. 2 C. 3 D. 4
9.如图,点 O为线段 AB的中点,点 B,C,D到点 O的距离相等,连接 AC,BD. 则下面结
论不.一.定.成立的是
A.∠ACB=90° B.∠BDC=∠BAC
C. AC平分∠BAD D. ∠BCD+∠BAD=180°
10.如图,点 A,B的坐标分别为 A(2,0),B(0,2),点 C为坐标平面内一点,BC=1,点 M为
线段 AC的中点,连接 OM,则线段 OM的最大值为( )
2 1A. 2 B. 2 2 C.2 2 1 D. 2
二、填空题(本题共 16分,每小题 2分)
11.若关于 x的方程 x2 mx m 0有两个相等实根,则代数式 2m2 8m 1的值为 .
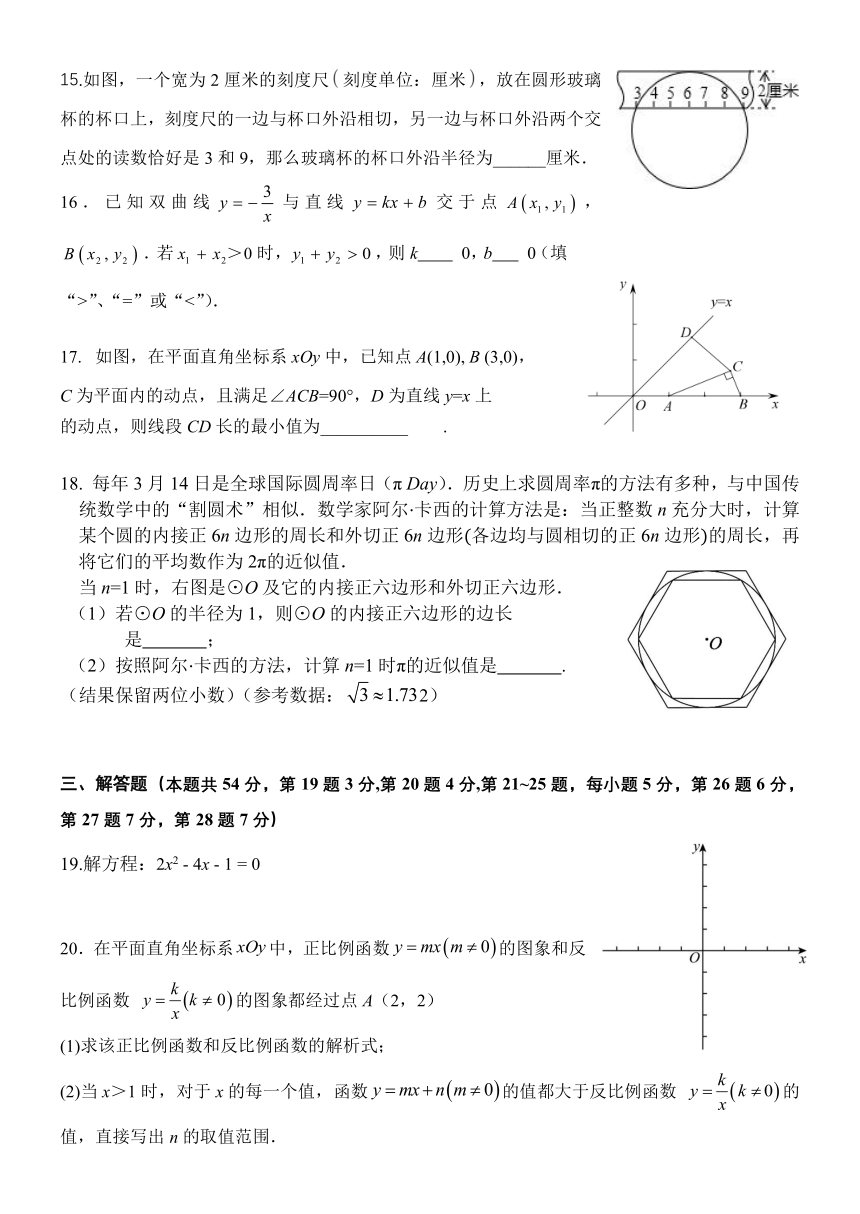
12.如图,AB是⊙O的直径,PA,PC分别与⊙O相切于点 A,点 C,若∠P 60°,PA 3 ,则
AB的长为 .
13.如图,在 Rt△ABC中,∠ABC=90°,AB=BC=3,点 D在 AC上,且 AD=2,将点 D绕着点 A
顺时针方向旋转,使得点 D的对应点 E恰好落在 AB边上,则旋转角的度数为 ,
CE的长为 .
第 12题图 第 13题图 第 14题图
14.在平面直角坐标系 xOy y kx b(k m中,一次函数 0)与反比例函数 y (m 0)的图象交于点
x
A( 2,3), B(1,a) , 不等式 kx b
m
的解集是
x
15.如图,一个宽为 2厘米的刻度尺 刻度单位:厘米 ,放在圆形玻璃
杯的杯口上,刻度尺的一边与杯口外沿相切,另一边与杯口外沿两个交
点处的读数恰好是 3和 9,那么玻璃杯的杯口外沿半径为______厘米.
16 3. 已 知 双 曲 线 y 与 直 线 y kx b 交 于 点 A x , y ,
x 1 1
B x2 , y2 .若 x1 x2>0 时,y1 y2 0,则 k 0,b 0(填
“>”、“=”或“<”).
17. 如图,在平面直角坐标系 xOy中,已知点 A(1,0), B (3,0),
C为平面内的动点,且满足∠ACB=90°,D为直线 y=x上
的动点,则线段 CD长的最小值为__________ .
18. 每年 3月 14日是全球国际圆周率日(π Day).历史上求圆周率π的方法有多种,与中国传
统数学中的“割圆术”相似.数学家阿尔 卡西的计算方法是:当正整数 n充分大时,计算
某个圆的内接正 6n边形的周长和外切正 6n边形(各边均与圆相切的正 6n边形)的周长,再
将它们的平均数作为 2π的近似值.
当 n=1时,右图是⊙O及它的内接正六边形和外切正六边形.
(1)若⊙O的半径为 1,则⊙O的内接正六边形的边长
是 ;
(2)按照阿尔 卡西的方法,计算 n=1时π的近似值是 .
(结果保留两位小数)(参考数据: 3 1.732)
三、解答题(本题共 54分,第 19题 3分,第 20题 4分,第 21~25题,每小题 5分,第 26题 6分,
第 27题 7分,第 28题 7分)
19.解方程:2x2 - 4x - 1 = 0
20.在平面直角坐标系 xOy中,正比例函数 y mx m 0 的图象和反
k
比例函数 y k 0 的图象都经过点 A(2,2)
x
(1)求该正比例函数和反比例函数的解析式;
k
(2)当 x>1时,对于 x的每一个值,函数 y mx n m 0 的值都大于反比例函数 y k 0 的
x
值,直接写出 n的取值范围.
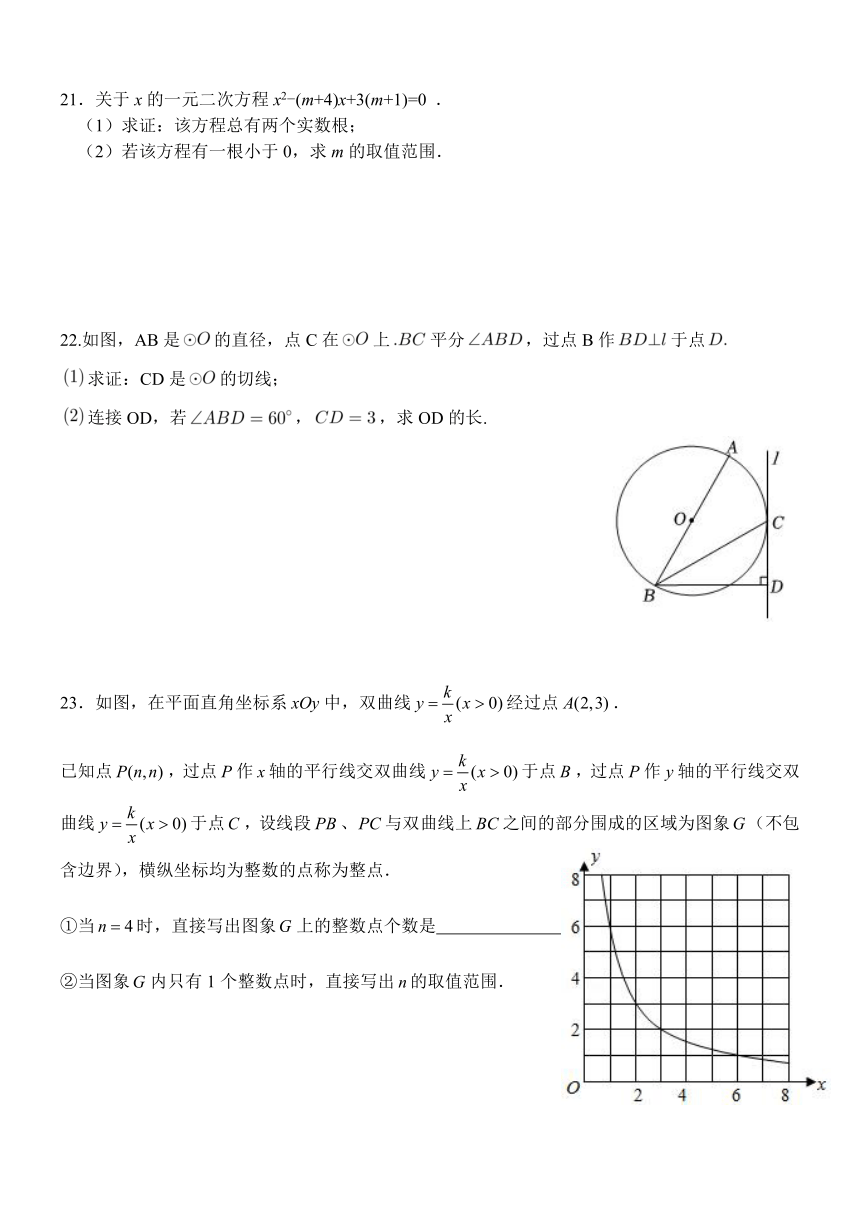
21.关于 x的一元二次方程 x2-(m+4)x+3(m+1)=0 .
(1)求证:该方程总有两个实数根;
(2)若该方程有一根小于 0,求 m的取值范围.
22.如图,AB是 的直径,点 C在 上 平分 ,过点 B作 于点
求证:CD是 的切线;
连接 OD,若 , ,求 OD的长.
23 k.如图,在平面直角坐标系 xOy中,双曲线 y (x 0)经过点 A(2,3).
x
k
已知点 P(n,n),过点 P作 x轴的平行线交双曲线 y (x 0)于点 B,过点 P作 y轴的平行线交双
x
k
曲线 y (x 0)于点C,设线段 PB、PC与双曲线上 BC之间的部分围成的区域为图象G(不包
x
含边界),横纵坐标均为整数的点称为整点.
①当 n 4时,直接写出图象G上的整数点个数是 ;
②当图象G内只有 1个整数点时,直接写出 n的取值范围.
1
24.小平在学习过程中遇到一个函数 y x .
x 2
下面是小平对其研究的过程,请补充完整:
1
(1)函数 y x的自变量 x的取值范围是 ;
x 2
(2)下表是 y 与 x的几组对应值.
x … 2 1 0 1 1.5 1.8 2.2 2.5 3 4 5 6 …
y … 1.75 0.67 0.5 2 3.5 6.8 7.2 4.5 m 4.5 5.33 6.25 …
其中m的值为 ;
(3)①根据表格中的数据,在平面直角坐标系 xOy中,画出函数图象;
②写出此函数图象的增减性:
③过点 (0,n)作平行于 x轴的直线 l,结合图象解决问题:若直线 l与函数
y 1 x的图象有三个交点,则 n的取值范围是 .
x 2
25.如图,在 △ 中,∠ = 90°,点 为 边的中点,以 为直径作⊙ ,分别与 ,
交于点 , ,过点 作 ⊥ 于 .
(1)求证: 是⊙ 的切线;
(2)若 = 6,⊙ 的半径为 5,求 的长
26.在平面直角坐标系 xOy中,点 A(﹣1,m),点 B(3,n)在抛物线 y=ax2+bx+c(a>0)上.设
抛物线的对称轴为直线 x=t.
(1)当 t=2时,
①直接写出 b与 a满足的等量关系;
②比较 m,n的大小,并说明理由;
(2)已知点 C(x0,p)在该抛物线上,若对于 3<x0<4,都有 m>p>n,求 t的取值范围.
27.如图,在△ABC中,AB=AC,点 D,E分别在边 AC,BC上,连接 DE,∠EDC=∠B.
(1)求证:ED=EC;
(2)连接 BD,点 F为 BD的中点,连接 AF,EF.
①依题意补全图形;
②若 AF⊥EF,求∠BAC的大小.
28. 在平面直角坐标系 xOy中, O的半径为 2,点 P、Q是平面内的点,如果点 P关于点 Q的
中心对称点在 O上,我们称圆上的点为点 P关于点 Q的“等距点”.
(1)已知如图 1点 P(4,0).
①如图 1,在点Q1 3,0 ,Q2 2, 1 ,Q3 1,1 中, O上存在点 P关于点 Q的“等距点”的是
________;
②如图 2,点Q m,n , O上存在点 P关于点 Q的“等距点”,则 m的取值范围是________;
(2)如图 3,已知点Q 1,1 ,点 P在 y x b的图象上,若 O上存在点 P关于点 Q的“等距
点”,求 b的取值范围.
班级: 姓名: 2024.12
一、选择题(本题共 30 分,每小题 3 分)
1. 函数 y (x 1)2 2的最小值是
A.1 B.-1 C.2 D.-2
2. 2点 A( 1,y1), B(1,y2),C(2,y3)是反比例函数 y 图象上的三个点,则 y1 ,y2 ,y3 的x
大小关系是
A. y3 y2 y1 B. y1 y3 y2 C. y2 y3 y1 D. y3 y1 y2
3.方程 x2 - x + 3 = 0的根的情况是
A.有两个不相等的实数根 B.有两个相等的实数根
C.无实数根 D.只有一个实数根
4 2.如图,在平面直角坐标系 xOy中,B是反比例函数 y = (x > 0)的图象上的
x
一点,则矩形 OABC的面积为
A.1 B. 2
C.3 D. 4
5.如图,将△ABC绕点 A逆时针旋转 100°,得到△ADE.若点 D在线段
BC的延长线上,则 B的大小为
A.30° B.40°
C.50° D.60°
6.一个扇形的圆心角是 120°,面积为 3πcm2,那么这个扇形的半径是
A. 1cm B. 3cm C. 6cm D. 9cm
k
7.如图,反比例函数 y 的图象经过点 A(4,1),当 y 1时,x的取值
x
范围是
A. x 0或 x 4 B. 0 x 4
C. x 4 D. x 4
8.抛物线 y x 1 2 t与 x轴的两个交点之间的距离为 4,则 t 的值是
A. 1 B. 2 C. 3 D. 4
9.如图,点 O为线段 AB的中点,点 B,C,D到点 O的距离相等,连接 AC,BD. 则下面结
论不.一.定.成立的是
A.∠ACB=90° B.∠BDC=∠BAC
C. AC平分∠BAD D. ∠BCD+∠BAD=180°
10.如图,点 A,B的坐标分别为 A(2,0),B(0,2),点 C为坐标平面内一点,BC=1,点 M为
线段 AC的中点,连接 OM,则线段 OM的最大值为( )
2 1A. 2 B. 2 2 C.2 2 1 D. 2
二、填空题(本题共 16分,每小题 2分)
11.若关于 x的方程 x2 mx m 0有两个相等实根,则代数式 2m2 8m 1的值为 .
12.如图,AB是⊙O的直径,PA,PC分别与⊙O相切于点 A,点 C,若∠P 60°,PA 3 ,则
AB的长为 .
13.如图,在 Rt△ABC中,∠ABC=90°,AB=BC=3,点 D在 AC上,且 AD=2,将点 D绕着点 A
顺时针方向旋转,使得点 D的对应点 E恰好落在 AB边上,则旋转角的度数为 ,
CE的长为 .
第 12题图 第 13题图 第 14题图
14.在平面直角坐标系 xOy y kx b(k m中,一次函数 0)与反比例函数 y (m 0)的图象交于点
x
A( 2,3), B(1,a) , 不等式 kx b
m
的解集是
x
15.如图,一个宽为 2厘米的刻度尺 刻度单位:厘米 ,放在圆形玻璃
杯的杯口上,刻度尺的一边与杯口外沿相切,另一边与杯口外沿两个交
点处的读数恰好是 3和 9,那么玻璃杯的杯口外沿半径为______厘米.
16 3. 已 知 双 曲 线 y 与 直 线 y kx b 交 于 点 A x , y ,
x 1 1
B x2 , y2 .若 x1 x2>0 时,y1 y2 0,则 k 0,b 0(填
“>”、“=”或“<”).
17. 如图,在平面直角坐标系 xOy中,已知点 A(1,0), B (3,0),
C为平面内的动点,且满足∠ACB=90°,D为直线 y=x上
的动点,则线段 CD长的最小值为__________ .
18. 每年 3月 14日是全球国际圆周率日(π Day).历史上求圆周率π的方法有多种,与中国传
统数学中的“割圆术”相似.数学家阿尔 卡西的计算方法是:当正整数 n充分大时,计算
某个圆的内接正 6n边形的周长和外切正 6n边形(各边均与圆相切的正 6n边形)的周长,再
将它们的平均数作为 2π的近似值.
当 n=1时,右图是⊙O及它的内接正六边形和外切正六边形.
(1)若⊙O的半径为 1,则⊙O的内接正六边形的边长
是 ;
(2)按照阿尔 卡西的方法,计算 n=1时π的近似值是 .
(结果保留两位小数)(参考数据: 3 1.732)
三、解答题(本题共 54分,第 19题 3分,第 20题 4分,第 21~25题,每小题 5分,第 26题 6分,
第 27题 7分,第 28题 7分)
19.解方程:2x2 - 4x - 1 = 0
20.在平面直角坐标系 xOy中,正比例函数 y mx m 0 的图象和反
k
比例函数 y k 0 的图象都经过点 A(2,2)
x
(1)求该正比例函数和反比例函数的解析式;
k
(2)当 x>1时,对于 x的每一个值,函数 y mx n m 0 的值都大于反比例函数 y k 0 的
x
值,直接写出 n的取值范围.
21.关于 x的一元二次方程 x2-(m+4)x+3(m+1)=0 .
(1)求证:该方程总有两个实数根;
(2)若该方程有一根小于 0,求 m的取值范围.
22.如图,AB是 的直径,点 C在 上 平分 ,过点 B作 于点
求证:CD是 的切线;
连接 OD,若 , ,求 OD的长.
23 k.如图,在平面直角坐标系 xOy中,双曲线 y (x 0)经过点 A(2,3).
x
k
已知点 P(n,n),过点 P作 x轴的平行线交双曲线 y (x 0)于点 B,过点 P作 y轴的平行线交双
x
k
曲线 y (x 0)于点C,设线段 PB、PC与双曲线上 BC之间的部分围成的区域为图象G(不包
x
含边界),横纵坐标均为整数的点称为整点.
①当 n 4时,直接写出图象G上的整数点个数是 ;
②当图象G内只有 1个整数点时,直接写出 n的取值范围.
1
24.小平在学习过程中遇到一个函数 y x .
x 2
下面是小平对其研究的过程,请补充完整:
1
(1)函数 y x的自变量 x的取值范围是 ;
x 2
(2)下表是 y 与 x的几组对应值.
x … 2 1 0 1 1.5 1.8 2.2 2.5 3 4 5 6 …
y … 1.75 0.67 0.5 2 3.5 6.8 7.2 4.5 m 4.5 5.33 6.25 …
其中m的值为 ;
(3)①根据表格中的数据,在平面直角坐标系 xOy中,画出函数图象;
②写出此函数图象的增减性:
③过点 (0,n)作平行于 x轴的直线 l,结合图象解决问题:若直线 l与函数
y 1 x的图象有三个交点,则 n的取值范围是 .
x 2
25.如图,在 △ 中,∠ = 90°,点 为 边的中点,以 为直径作⊙ ,分别与 ,
交于点 , ,过点 作 ⊥ 于 .
(1)求证: 是⊙ 的切线;
(2)若 = 6,⊙ 的半径为 5,求 的长
26.在平面直角坐标系 xOy中,点 A(﹣1,m),点 B(3,n)在抛物线 y=ax2+bx+c(a>0)上.设
抛物线的对称轴为直线 x=t.
(1)当 t=2时,
①直接写出 b与 a满足的等量关系;
②比较 m,n的大小,并说明理由;
(2)已知点 C(x0,p)在该抛物线上,若对于 3<x0<4,都有 m>p>n,求 t的取值范围.
27.如图,在△ABC中,AB=AC,点 D,E分别在边 AC,BC上,连接 DE,∠EDC=∠B.
(1)求证:ED=EC;
(2)连接 BD,点 F为 BD的中点,连接 AF,EF.
①依题意补全图形;
②若 AF⊥EF,求∠BAC的大小.
28. 在平面直角坐标系 xOy中, O的半径为 2,点 P、Q是平面内的点,如果点 P关于点 Q的
中心对称点在 O上,我们称圆上的点为点 P关于点 Q的“等距点”.
(1)已知如图 1点 P(4,0).
①如图 1,在点Q1 3,0 ,Q2 2, 1 ,Q3 1,1 中, O上存在点 P关于点 Q的“等距点”的是
________;
②如图 2,点Q m,n , O上存在点 P关于点 Q的“等距点”,则 m的取值范围是________;
(2)如图 3,已知点Q 1,1 ,点 P在 y x b的图象上,若 O上存在点 P关于点 Q的“等距
点”,求 b的取值范围.
同课章节目录
