2024-2025学年江苏省扬州市梅岭集团八年级(上)11月期中数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年江苏省扬州市梅岭集团八年级(上)11月期中数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 582.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-07 13:19:56 | ||
图片预览

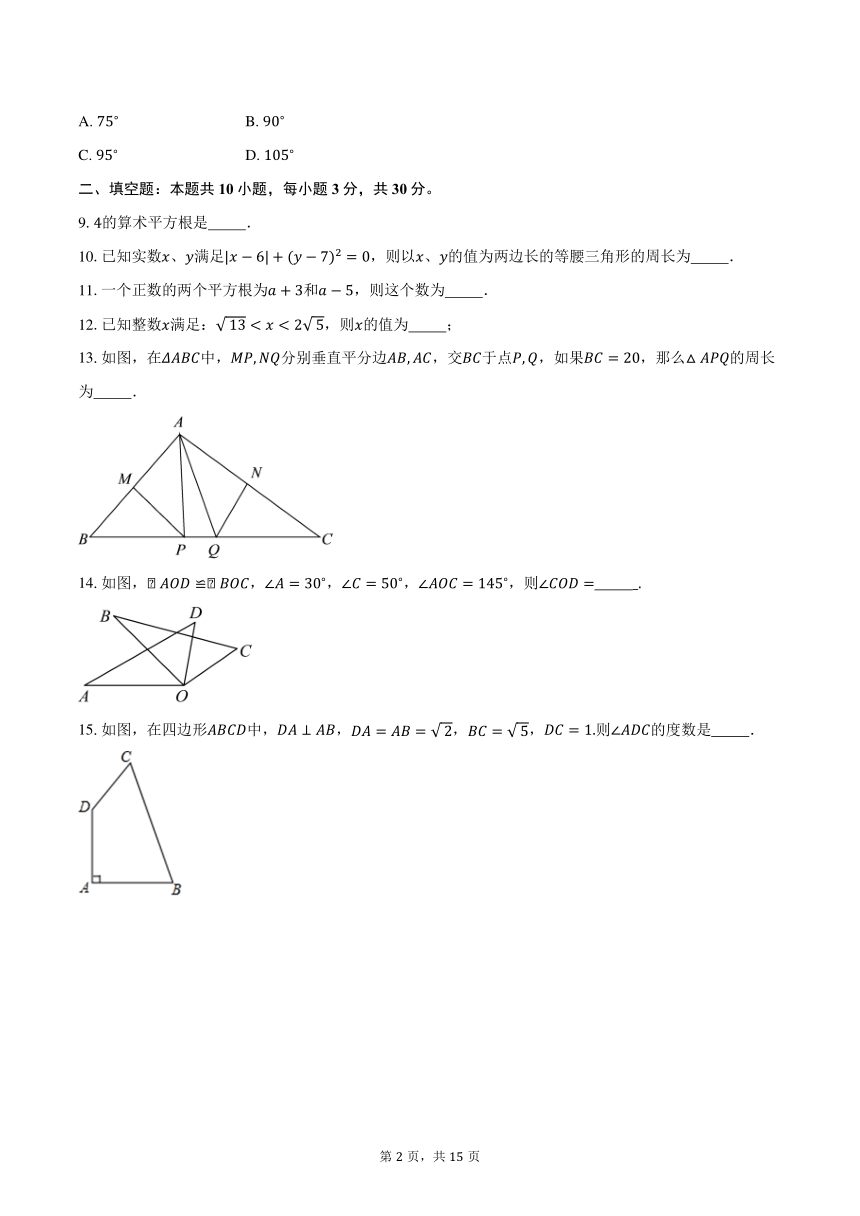
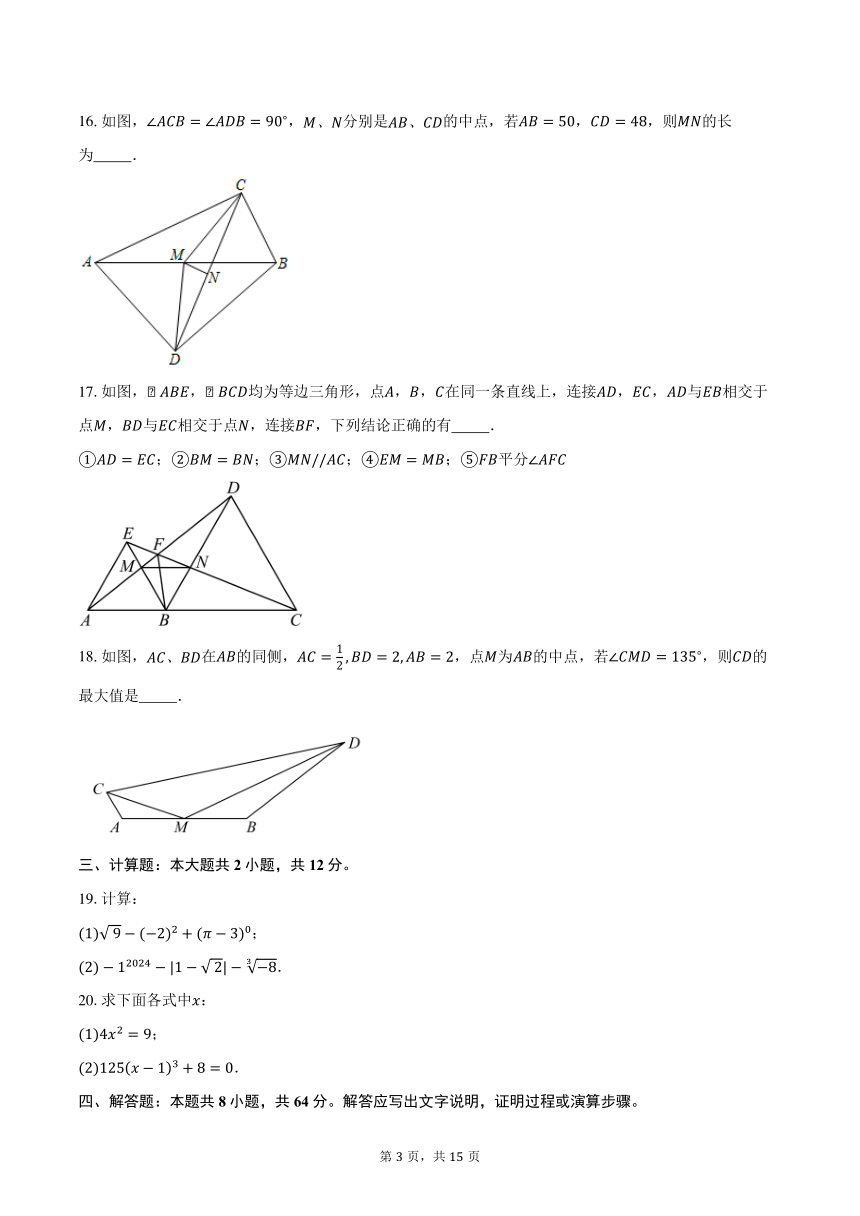


文档简介
2024-2025学年江苏省扬州市梅岭集团八年级(上)11月期中数学试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在“回收”、“节水”、“绿色食品”、“低碳”四个标志图案中.轴对称图形是( )
A. B. C. D.
2.在实数,,,,,,中,无理数的个数是( )
A. 个 B. 个 C. 个 D. 个
3.我市某部门年年初收入预算为元,关于近似数,是精确到( )
A. 百分位 B. 百位 C. 千位 D. 万位
4.、、三名选手站在一个三角形的三个顶点的位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在的( )
A. 三边中线的交点 B. 三边垂直平分线的交点
C. 三条角平分线的交点 D. 三边上高的交点
5.在下列四组数中,属于勾股数的是( )
A. ,, B. ,, C. ,, D. ,,
6.根据下列条件,能画出唯一的是( )
A. ,, B. ,,
C. ,, D. ,
7.如图,是一钢架,,为使钢架更加牢固,需在其内部添加一些钢管、、,添的钢管长度都与相等,则最多能添加这样的钢管( )
A. 根 B. 根 C. 根 D. 根
8.如图,为等边的高,、分别为线段上的动点,且,当取最小值时,的度数为( )
A. B.
C. D.
二、填空题:本题共10小题,每小题3分,共30分。
9.的算术平方根是 .
10.已知实数、满足,则以、的值为两边长的等腰三角形的周长为 .
11.一个正数的两个平方根为和,则这个数为 .
12.已知整数满足:,则的值为 ;
13.如图,在中,分别垂直平分边,交于点,如果,那么的周长为 .
14.如图,,,,,则
15.如图,在四边形中,,,,则的度数是 .
16.如图,,分别是的中点,若,,则的长为 .
17.如图,,均为等边三角形,点,,在同一条直线上,连接,,与相交于点,与相交于点,连接,下列结论正确的有 .
;;;;平分
18.如图,在的同侧,,点为的中点,若,则的最大值是 .
三、计算题:本大题共2小题,共12分。
19.计算:
;
.
20.求下面各式中:
;
.
四、解答题:本题共8小题,共64分。解答应写出文字说明,证明过程或演算步骤。
21.本小题分
已知的平方根为,的立方根为,若是的整数部分,求的平方根.
22.本小题分
如图,在边长为的小正方形网格中,点,,均落在格点上.
画出关于直线的轴对称图形.
连接、,则的面积为 .
在直线上画出点,使的值最小,这个最小值是______.
23.本小题分
如图,是的边上一点.,交于点,.
求证:.
若,,求的长.
24.本小题分
九章算术中有一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其底面是边长为尺的正方形,一棵芦苇生长在它的中央,高出水面部分为尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部恰好碰到岸边.求水深和芦苇长各是多少尺?
25.本小题分
对于实数,我们规定:用符号表示不大于的最大整数,称为的根整数,例如:,.
仿照以上方法计算: ; .
若,写出满足题意的的整数值 .
如果我们对连续求根整数,直到结果为为止.例如:对连续求根整数次,这时候结果为.对连续求根整数, 次之后结果为.
只需进行次连续求根整数运算后结果为的所有正整数中,最大的是 .
26.本小题分
综合与实践
【背景介绍】勾股定理是几何学中的明珠,充满着魅力.如图是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是大正方形的面积有两种求法,一种是等于,另一种是等于四个直角三角形与一个小正方形的面积之和,即,从而得到等式,化简便得结论这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求
法”.
【方法运用】向常春在年构造发现了一个新的证法:把两个全等的直角和如图放置,,显然对角线互相垂直的四边形的面积等于对角线乘积的一半
请用,,分别表示出四边形,梯形的面积,再探究这三个图形面积之间的关系,证明勾股定理.
【方法迁移】请利用“双求法”解决下面的问题:如图,在中,,是边上的高,,求的长度;
如图,在中,是边上的高,,求的长.
27.本小题分
问题:如图,在中,,为边上一点不与点,重合,将线段绕点逆时针旋转得到,连接,则线段之间满足的等量关系式为 .
探索:如图,在与中,,将绕点旋转,使点落在边上,试探索线段之间满足的等量关系,并证明你的结论;
应用:如图,在四边形中,若,,求的长.
28.本小题分
在四边形中,,,.
为上一点,将沿直线翻折至的位置点落在点处.
如图,当点落在边上时,利用尺规作图,在图中作出满足条件的图形即的位置,不写作法,保留作图痕迹,并直接写出此时
如图,与相交于点,与相交于点,且,求的长.
如图,已知点为射线上的一个动点,将沿翻折,点恰好落在直线上的点处,求的长.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.或
11.
12.
13.
14.度
15.
16.
17.
18.
19.【小题】
解:
;
【小题】
解:
.
20.【小题】
解:
.
【小题】
解:
.
21.解:的平方根为,的立方根为,
,,
解得:,
,
,
的整数部分为,即,
,
而的平方根为,
的平方根.
22.【小题】
解:如图,即为所求;
【小题】
【小题】
解:如图,点即为所求,
,
由轴对称的性质可得,
,由两点之间线段最短可得,此时的值最小为,
由勾股定理可得.
23.【小题】
证明:,
,,
在和中,
;
【小题】
解:由可知,
,,
,
,
,即的长是.
24.解:依题意画出图形,设芦苇长尺,则水深尺,
因为尺,所以尺,
在中,,
解之得,
即水深尺,芦苇长尺.
25.【小题】
,,,
,
,,
故答案为:,;
【小题】
,,且,
,,,
故答案为:,,;
【小题】
第一次:,
第二次:,
第三次:,
故答案为:;
【小题】
最大的正整数是,
理由是:,,,
对只需进行次操作后变为,
,,,,
对只需进行次操作后变为,
只需进行次操作后变为的所有正整数中,最大的是;
故答案为:.
26.【小题】
解:,
,
,
,
,
化简得:;
【小题】
解:在中,,,
,
是边上的高,
,
;
【小题】
解:设,
在中,
,
,
,
在中,
,
,
,
.
27.【小题】
【小题】
探索:,
理由如下:连接,
由得,,
,
,
,
在中,,又,
;
【小题】
应用:过点作,使,连接,
,
即,
在和中,
,
,
,
,
,
,
.
28.【小题】
以点为圆心,长为半径画弧,交于点,再作的角平分线交于点,连接、,如下图:
则
由矩形的性质可知:
由折叠的性质,可设,
在和中
≌
,
在中,
解得,即
【小题】
点在线段上,
由翻折得,
,
点在延长线上
由翻折得
,
设
在中,
解得,即
综上所述,或
第1页,共1页
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在“回收”、“节水”、“绿色食品”、“低碳”四个标志图案中.轴对称图形是( )
A. B. C. D.
2.在实数,,,,,,中,无理数的个数是( )
A. 个 B. 个 C. 个 D. 个
3.我市某部门年年初收入预算为元,关于近似数,是精确到( )
A. 百分位 B. 百位 C. 千位 D. 万位
4.、、三名选手站在一个三角形的三个顶点的位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在的( )
A. 三边中线的交点 B. 三边垂直平分线的交点
C. 三条角平分线的交点 D. 三边上高的交点
5.在下列四组数中,属于勾股数的是( )
A. ,, B. ,, C. ,, D. ,,
6.根据下列条件,能画出唯一的是( )
A. ,, B. ,,
C. ,, D. ,
7.如图,是一钢架,,为使钢架更加牢固,需在其内部添加一些钢管、、,添的钢管长度都与相等,则最多能添加这样的钢管( )
A. 根 B. 根 C. 根 D. 根
8.如图,为等边的高,、分别为线段上的动点,且,当取最小值时,的度数为( )
A. B.
C. D.
二、填空题:本题共10小题,每小题3分,共30分。
9.的算术平方根是 .
10.已知实数、满足,则以、的值为两边长的等腰三角形的周长为 .
11.一个正数的两个平方根为和,则这个数为 .
12.已知整数满足:,则的值为 ;
13.如图,在中,分别垂直平分边,交于点,如果,那么的周长为 .
14.如图,,,,,则
15.如图,在四边形中,,,,则的度数是 .
16.如图,,分别是的中点,若,,则的长为 .
17.如图,,均为等边三角形,点,,在同一条直线上,连接,,与相交于点,与相交于点,连接,下列结论正确的有 .
;;;;平分
18.如图,在的同侧,,点为的中点,若,则的最大值是 .
三、计算题:本大题共2小题,共12分。
19.计算:
;
.
20.求下面各式中:
;
.
四、解答题:本题共8小题,共64分。解答应写出文字说明,证明过程或演算步骤。
21.本小题分
已知的平方根为,的立方根为,若是的整数部分,求的平方根.
22.本小题分
如图,在边长为的小正方形网格中,点,,均落在格点上.
画出关于直线的轴对称图形.
连接、,则的面积为 .
在直线上画出点,使的值最小,这个最小值是______.
23.本小题分
如图,是的边上一点.,交于点,.
求证:.
若,,求的长.
24.本小题分
九章算术中有一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其底面是边长为尺的正方形,一棵芦苇生长在它的中央,高出水面部分为尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部恰好碰到岸边.求水深和芦苇长各是多少尺?
25.本小题分
对于实数,我们规定:用符号表示不大于的最大整数,称为的根整数,例如:,.
仿照以上方法计算: ; .
若,写出满足题意的的整数值 .
如果我们对连续求根整数,直到结果为为止.例如:对连续求根整数次,这时候结果为.对连续求根整数, 次之后结果为.
只需进行次连续求根整数运算后结果为的所有正整数中,最大的是 .
26.本小题分
综合与实践
【背景介绍】勾股定理是几何学中的明珠,充满着魅力.如图是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是大正方形的面积有两种求法,一种是等于,另一种是等于四个直角三角形与一个小正方形的面积之和,即,从而得到等式,化简便得结论这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求
法”.
【方法运用】向常春在年构造发现了一个新的证法:把两个全等的直角和如图放置,,显然对角线互相垂直的四边形的面积等于对角线乘积的一半
请用,,分别表示出四边形,梯形的面积,再探究这三个图形面积之间的关系,证明勾股定理.
【方法迁移】请利用“双求法”解决下面的问题:如图,在中,,是边上的高,,求的长度;
如图,在中,是边上的高,,求的长.
27.本小题分
问题:如图,在中,,为边上一点不与点,重合,将线段绕点逆时针旋转得到,连接,则线段之间满足的等量关系式为 .
探索:如图,在与中,,将绕点旋转,使点落在边上,试探索线段之间满足的等量关系,并证明你的结论;
应用:如图,在四边形中,若,,求的长.
28.本小题分
在四边形中,,,.
为上一点,将沿直线翻折至的位置点落在点处.
如图,当点落在边上时,利用尺规作图,在图中作出满足条件的图形即的位置,不写作法,保留作图痕迹,并直接写出此时
如图,与相交于点,与相交于点,且,求的长.
如图,已知点为射线上的一个动点,将沿翻折,点恰好落在直线上的点处,求的长.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.或
11.
12.
13.
14.度
15.
16.
17.
18.
19.【小题】
解:
;
【小题】
解:
.
20.【小题】
解:
.
【小题】
解:
.
21.解:的平方根为,的立方根为,
,,
解得:,
,
,
的整数部分为,即,
,
而的平方根为,
的平方根.
22.【小题】
解:如图,即为所求;
【小题】
【小题】
解:如图,点即为所求,
,
由轴对称的性质可得,
,由两点之间线段最短可得,此时的值最小为,
由勾股定理可得.
23.【小题】
证明:,
,,
在和中,
;
【小题】
解:由可知,
,,
,
,
,即的长是.
24.解:依题意画出图形,设芦苇长尺,则水深尺,
因为尺,所以尺,
在中,,
解之得,
即水深尺,芦苇长尺.
25.【小题】
,,,
,
,,
故答案为:,;
【小题】
,,且,
,,,
故答案为:,,;
【小题】
第一次:,
第二次:,
第三次:,
故答案为:;
【小题】
最大的正整数是,
理由是:,,,
对只需进行次操作后变为,
,,,,
对只需进行次操作后变为,
只需进行次操作后变为的所有正整数中,最大的是;
故答案为:.
26.【小题】
解:,
,
,
,
,
化简得:;
【小题】
解:在中,,,
,
是边上的高,
,
;
【小题】
解:设,
在中,
,
,
,
在中,
,
,
,
.
27.【小题】
【小题】
探索:,
理由如下:连接,
由得,,
,
,
,
在中,,又,
;
【小题】
应用:过点作,使,连接,
,
即,
在和中,
,
,
,
,
,
,
.
28.【小题】
以点为圆心,长为半径画弧,交于点,再作的角平分线交于点,连接、,如下图:
则
由矩形的性质可知:
由折叠的性质,可设,
在和中
≌
,
在中,
解得,即
【小题】
点在线段上,
由翻折得,
,
点在延长线上
由翻折得
,
设
在中,
解得,即
综上所述,或
第1页,共1页
同课章节目录
