上海市杨浦高级中学2016届高三3月月考数学(文理)试题
文档属性
| 名称 | 上海市杨浦高级中学2016届高三3月月考数学(文理)试题 | 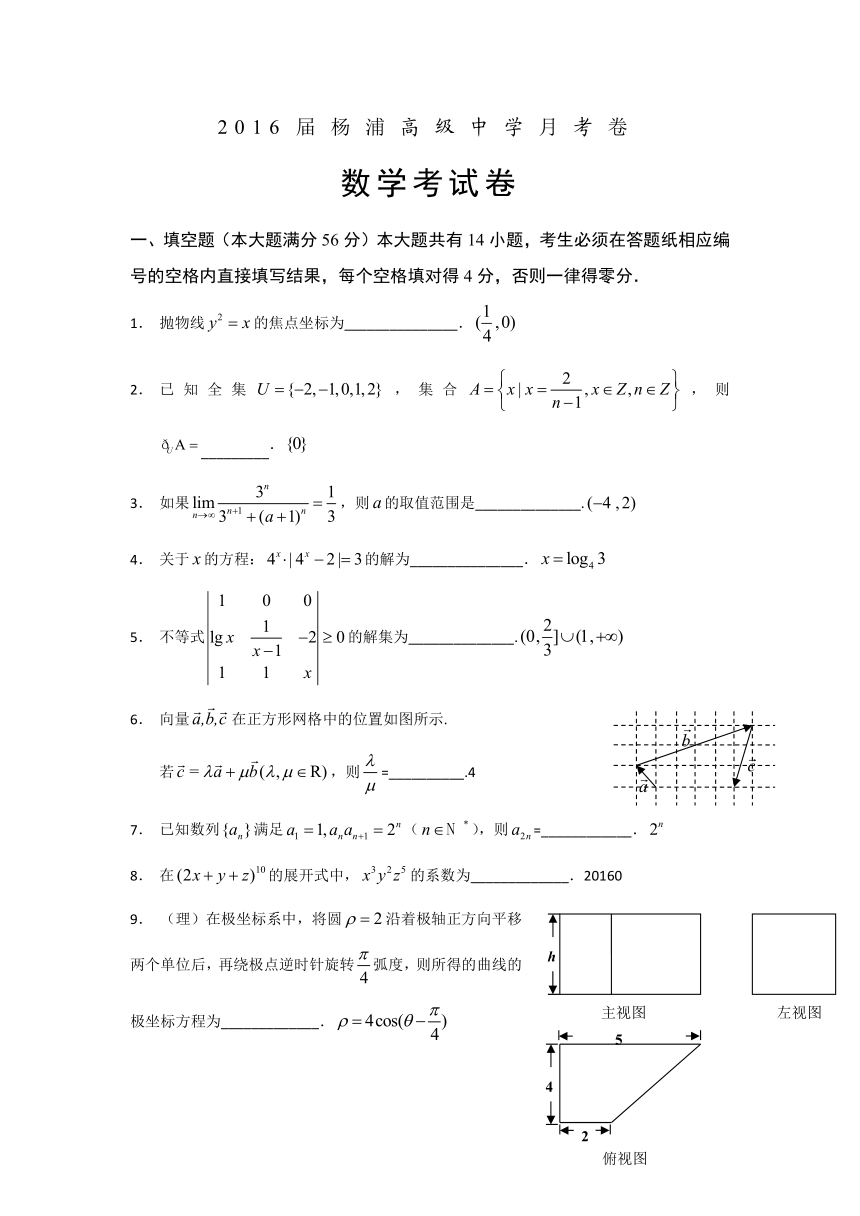 | |
| 格式 | zip | ||
| 文件大小 | 415.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-31 08:04:04 | ||
图片预览





文档简介
2016届杨浦高级中学月考卷
数学考试卷
一、填空题(本大题满分56分)本大题共有14小题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.
抛物线的焦点坐标为_______________.
已知全集,集合,则_________.
如果,则的取值范围是______________.
关于的方程:的解为_______________.
不等式的解集为______________.
向量在正方形网格中的位置如图所示.
若,则=__________.4
已知数列满足(),则=____________.
在的展开式中,的系数为_____________.20160
(理)在极坐标系中,将圆沿着极轴正方向平移两个单位后,再绕极点逆时针旋转弧度,则所得的曲线的极坐标方程为_____________.
(文)一个几何体的三视图如图所示.若该几何体的表面积为,则其高=_____________.4
10. 5位好朋友相约乘坐迪士尼乐园的环园小火车。小火车的车厢共有4节,设每一位乘客进入每节车厢是等可能的,则这5位好朋友无人落单(即一节车厢内,至少有5人中的2人)的概率是___________.
11. 已知定义在上的函数对于任意的都满足.当时,.若函数至少有6个零点,则的取值范围是____________.
12. (理)一个篮球运动员投篮一次得3分的概率为,得2分的概率为(),不得分的概率为.若他投篮一次得分的数学期望,则的取值范围是_____________.
(文)设全集,,若恒成立,则实数的最大值是___________.
13.(理) 在实数集中,我们定义的大小关系“”为全体实数排了一个“序”。类似的,我们在复数集上,也可以定义一个称为“序”的关系,记为“” .定义如下:
对于任意两个复数,当且仅当“”或者“” .按上述定义的关系“”,给出如下四个命题:
① ;
② 若,则;
③ 若,则对任意,都有;
对于复数,若,则.
其中真命题的序号为____________________.①②③
(文)已知数列满足:(为正整数),,若,则所有可能的取值构成的集合为________________.
14. (理)符号表示数列的前项和(即)。已知数列满足(),记,若,则当取最小值时,=___________.(1007)
(文)在实数集中,我们定义的大小关系“”为全体实数排了一个“序”。类似的,我们在复数集上,也可以定义一个称为“序”的关系,记为“” .定义如下:
对于任意两个复数,当且仅当“”或者“” .按上述定义的关系“”,给出如下四个命题:
① ;
② 若,则;
③ 若,则对任意,都有;
④ 对于复数,若,则.
其中真命题的序号为____________________.①②③
二、选择题(本大题共有4题,满分20分)每题有且只有一个正确答案,考生应在答题纸的相应编号上,填写结果,选对得5分,否则一律得零分.
15. 在样本的频率分布直方图中,共有9 ( http: / / www.21cnjy.com )个小长方形,若第一个长方形的面积为0.02,前五个与后五个长方形的面积分别成等差数列且公差互为相反数,若样本容量为160,则中间一组(即第五组)的频数为( C )
A. 12 B. 24 C. 36 D. 48
16. 已知为双曲线的一个焦点,则点到的一条渐近线的距离为( A )
A. B. 3 C. D.
17. 将函数的图像向左平移个单位长度后所得到的图像关于轴对称,则的最小值为( B )
A. B. C. D.
18. 在半径为的球内有一内接正三棱锥。它的底面三个顶点恰好都在同一个大圆上,一个动点从三棱锥的一个顶点出发沿球面运动,经过其余三点后返回。则经过的最短路程是( C )
A. B. C. D.
三、解答题(本大题共有5题,满分74分)解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
19.(本题满分12分)本题共有2个小题,第1小题5分,第2小题7分。
如图:已知四棱锥,底面是边长为6的正方形,,面,
点是的中点,点是的中点,连接、、.
(1)求证:;
(2)求二面角的大小.
(文)(1)求证:
(2)求异面直线与所成角的大小.
(理)(1)解法1:取AB中点T,连接MT、NT,
① …………………… 2分
② …………………… 4分
由①②得
所以 …………………… 5分
解法2:分别以AD、AB、AP为x轴、y轴、z轴建立空间直角坐标系,
则…………………… 2分
得, …………………… 4分
…………………… 5分
(2)(理)取平面AMB的一个法向量为 …………………… 1分
设平面AMN的法向量,又,
由,取平面AMN的一个法向量,……………… 4分
设二面角为,则=…………… 7分
所以二面角的大小为
(文)分别取中点,连接,
所以异面直线与所成角的大小即相交直线与所成角的大小…………………… 2分
在中可求得,…………………… 4分
从而由余弦定理可求得,…………………… 6分
所以异面直线与所成角的大小为.…………………… 7分
20.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分。
已知向量和向量,且.
(1)求函数的最小正周期和最大值;
(2)(理)已知的三个内角分别为,若有,,求面积的最大值.
(文)已知的三个内角分别为,若有,,,求的长度.
解:(1)由条件得 ……………………2分
得 ……………………4分
则函数的最小正周期为,最大值为2……………………6分
(2)(理)由,得,
,即…………3分
又,,………………6分
当且仅当时取等号
(或由正弦定理得:,
当且仅当时取等号………………6分)
所以面积的最大值为.…………………8分
(文)由,得,
,即…………3分
由正弦定理得 ………………6分
得 …………………8分
21.(本题满分14分)本题共有2个小题,第1小题7分,第2小题7分。
某地拟模仿图(1)建造一座大型体育馆,其设计方案侧面的外轮廓线如图(2)所示:曲线是以点为圆心的圆的一部分,其中;曲线是抛物线的一部分;,且恰好等于圆的半径.
若要求米,米,求与值;
当时,若要求体育馆侧面的最大宽度不超过米,求的取值范围.
解:(1)因为,解得. …………… 3分
此时圆,令,得,
所以,
将点代入中,解得. ………… 7分
(2)因为圆的半径为,所以,在中令,,则由题意知对恒成立,………… 9分
所以恒成立,而,当,即时,
由()递减,可知:当取最小值…… 12分
故,解得. …………14分
22.(本题满分16分)本题共有3个小题,第1小题4分,第2小题6分,第3小题6分。
如图数表:
每一行都是首项为1的等差数列,第行的公差为,且每一列也是等差数列,设第行的第项为.
(1)证明:成等差数列,并用表示();
(2)当时,将数列分组如下:
(),(),(),…(每组数的个数构成等差数列). 设前组中所有数之和为,求数列的前项和;
(3)在(2)的条件下,设是不超过20的正整数,当时,求使得不等式恒成立的所有的值.
解:(1) 由题意,,且,
得,即
所以成等差数列 .............2分
由且
即
化简得 ...............4分
当时, ...................6分
按数列分组规律,第组中有个奇数,
所以第1组到第组共有个奇数.
则前个奇数的和为, ...................................7分
即, ...............................8分
从而
利用“错位相减法”得 .................................10分
由得.
令 ........................12分
当时,都有,即.......................13分
而,
且当时,单调递增,故有. ..............................14分
所以,满足条件的所有正整数. ..............................16分
23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
如图,圆与直线相切于点,与正半轴交于点,与直线在第一象限的交点为. 点为圆上任一点,且满足,以为坐标的动点的轨迹记为曲线.
(1)求圆的方程及曲线的方程;
(2)若两条直线和分别交曲线于点和,求四边形面积的最大值,并求此时的的值.
(3)(理科)①根据曲线的方程,研究曲线的对称性,并证明曲线为椭圆.
(文科)已知曲线的轨迹为椭圆,研究曲线的对称性,并求椭圆的焦点坐标.
解:(1)由题意圆的半径,
故圆的方程为. ………………2分
由得,,将代入
得()为曲线的方程.
(未写范围不扣分)…………4分
(2)由
得,,
所以,同理 ( http: / / www.21cnjy.com ). ……………6分
由题意知 ,所以四边形的面积.
( http: / / www.21cnjy.com )
∵ ,∴ . …………8分
当且仅当时等号成立,此时.
∴ 当时,四边形的面积最大值为. ………………10分
(3) 曲线的方程为(),它关于直线、和原点对称,………11分
下面证明:
设曲线上任一点的坐标为,则,点关于直线的对称点为,显然,所以点在曲线上,故曲线关于直线对称,
同理曲线关于直线和原点对称. ………12分
证明:求得和直线的交点坐标为,
和直线的交点坐标为,
,,,.
在上取点 .
设为曲线上任一点,则
(因为)
.
即曲线上任一点到两定点的距离之和为定值.
若点到两定点的距离之和为定值,可以求得点的轨迹方程为(过程略).
故曲线是椭圆,其焦点坐标为. ………………18分
h
4
2
5
主视图
俯视图
左视图
样本数据
频率
组距
P
N
B
A
D
M
C
第19题图
图(1)
x
y
O
A
B
C
D
图(2)
E
·
F
数学考试卷
一、填空题(本大题满分56分)本大题共有14小题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.
抛物线的焦点坐标为_______________.
已知全集,集合,则_________.
如果,则的取值范围是______________.
关于的方程:的解为_______________.
不等式的解集为______________.
向量在正方形网格中的位置如图所示.
若,则=__________.4
已知数列满足(),则=____________.
在的展开式中,的系数为_____________.20160
(理)在极坐标系中,将圆沿着极轴正方向平移两个单位后,再绕极点逆时针旋转弧度,则所得的曲线的极坐标方程为_____________.
(文)一个几何体的三视图如图所示.若该几何体的表面积为,则其高=_____________.4
10. 5位好朋友相约乘坐迪士尼乐园的环园小火车。小火车的车厢共有4节,设每一位乘客进入每节车厢是等可能的,则这5位好朋友无人落单(即一节车厢内,至少有5人中的2人)的概率是___________.
11. 已知定义在上的函数对于任意的都满足.当时,.若函数至少有6个零点,则的取值范围是____________.
12. (理)一个篮球运动员投篮一次得3分的概率为,得2分的概率为(),不得分的概率为.若他投篮一次得分的数学期望,则的取值范围是_____________.
(文)设全集,,若恒成立,则实数的最大值是___________.
13.(理) 在实数集中,我们定义的大小关系“”为全体实数排了一个“序”。类似的,我们在复数集上,也可以定义一个称为“序”的关系,记为“” .定义如下:
对于任意两个复数,当且仅当“”或者“” .按上述定义的关系“”,给出如下四个命题:
① ;
② 若,则;
③ 若,则对任意,都有;
对于复数,若,则.
其中真命题的序号为____________________.①②③
(文)已知数列满足:(为正整数),,若,则所有可能的取值构成的集合为________________.
14. (理)符号表示数列的前项和(即)。已知数列满足(),记,若,则当取最小值时,=___________.(1007)
(文)在实数集中,我们定义的大小关系“”为全体实数排了一个“序”。类似的,我们在复数集上,也可以定义一个称为“序”的关系,记为“” .定义如下:
对于任意两个复数,当且仅当“”或者“” .按上述定义的关系“”,给出如下四个命题:
① ;
② 若,则;
③ 若,则对任意,都有;
④ 对于复数,若,则.
其中真命题的序号为____________________.①②③
二、选择题(本大题共有4题,满分20分)每题有且只有一个正确答案,考生应在答题纸的相应编号上,填写结果,选对得5分,否则一律得零分.
15. 在样本的频率分布直方图中,共有9 ( http: / / www.21cnjy.com )个小长方形,若第一个长方形的面积为0.02,前五个与后五个长方形的面积分别成等差数列且公差互为相反数,若样本容量为160,则中间一组(即第五组)的频数为( C )
A. 12 B. 24 C. 36 D. 48
16. 已知为双曲线的一个焦点,则点到的一条渐近线的距离为( A )
A. B. 3 C. D.
17. 将函数的图像向左平移个单位长度后所得到的图像关于轴对称,则的最小值为( B )
A. B. C. D.
18. 在半径为的球内有一内接正三棱锥。它的底面三个顶点恰好都在同一个大圆上,一个动点从三棱锥的一个顶点出发沿球面运动,经过其余三点后返回。则经过的最短路程是( C )
A. B. C. D.
三、解答题(本大题共有5题,满分74分)解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
19.(本题满分12分)本题共有2个小题,第1小题5分,第2小题7分。
如图:已知四棱锥,底面是边长为6的正方形,,面,
点是的中点,点是的中点,连接、、.
(1)求证:;
(2)求二面角的大小.
(文)(1)求证:
(2)求异面直线与所成角的大小.
(理)(1)解法1:取AB中点T,连接MT、NT,
① …………………… 2分
② …………………… 4分
由①②得
所以 …………………… 5分
解法2:分别以AD、AB、AP为x轴、y轴、z轴建立空间直角坐标系,
则…………………… 2分
得, …………………… 4分
…………………… 5分
(2)(理)取平面AMB的一个法向量为 …………………… 1分
设平面AMN的法向量,又,
由,取平面AMN的一个法向量,……………… 4分
设二面角为,则=…………… 7分
所以二面角的大小为
(文)分别取中点,连接,
所以异面直线与所成角的大小即相交直线与所成角的大小…………………… 2分
在中可求得,…………………… 4分
从而由余弦定理可求得,…………………… 6分
所以异面直线与所成角的大小为.…………………… 7分
20.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分。
已知向量和向量,且.
(1)求函数的最小正周期和最大值;
(2)(理)已知的三个内角分别为,若有,,求面积的最大值.
(文)已知的三个内角分别为,若有,,,求的长度.
解:(1)由条件得 ……………………2分
得 ……………………4分
则函数的最小正周期为,最大值为2……………………6分
(2)(理)由,得,
,即…………3分
又,,………………6分
当且仅当时取等号
(或由正弦定理得:,
当且仅当时取等号………………6分)
所以面积的最大值为.…………………8分
(文)由,得,
,即…………3分
由正弦定理得 ………………6分
得 …………………8分
21.(本题满分14分)本题共有2个小题,第1小题7分,第2小题7分。
某地拟模仿图(1)建造一座大型体育馆,其设计方案侧面的外轮廓线如图(2)所示:曲线是以点为圆心的圆的一部分,其中;曲线是抛物线的一部分;,且恰好等于圆的半径.
若要求米,米,求与值;
当时,若要求体育馆侧面的最大宽度不超过米,求的取值范围.
解:(1)因为,解得. …………… 3分
此时圆,令,得,
所以,
将点代入中,解得. ………… 7分
(2)因为圆的半径为,所以,在中令,,则由题意知对恒成立,………… 9分
所以恒成立,而,当,即时,
由()递减,可知:当取最小值…… 12分
故,解得. …………14分
22.(本题满分16分)本题共有3个小题,第1小题4分,第2小题6分,第3小题6分。
如图数表:
每一行都是首项为1的等差数列,第行的公差为,且每一列也是等差数列,设第行的第项为.
(1)证明:成等差数列,并用表示();
(2)当时,将数列分组如下:
(),(),(),…(每组数的个数构成等差数列). 设前组中所有数之和为,求数列的前项和;
(3)在(2)的条件下,设是不超过20的正整数,当时,求使得不等式恒成立的所有的值.
解:(1) 由题意,,且,
得,即
所以成等差数列 .............2分
由且
即
化简得 ...............4分
当时, ...................6分
按数列分组规律,第组中有个奇数,
所以第1组到第组共有个奇数.
则前个奇数的和为, ...................................7分
即, ...............................8分
从而
利用“错位相减法”得 .................................10分
由得.
令 ........................12分
当时,都有,即.......................13分
而,
且当时,单调递增,故有. ..............................14分
所以,满足条件的所有正整数. ..............................16分
23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
如图,圆与直线相切于点,与正半轴交于点,与直线在第一象限的交点为. 点为圆上任一点,且满足,以为坐标的动点的轨迹记为曲线.
(1)求圆的方程及曲线的方程;
(2)若两条直线和分别交曲线于点和,求四边形面积的最大值,并求此时的的值.
(3)(理科)①根据曲线的方程,研究曲线的对称性,并证明曲线为椭圆.
(文科)已知曲线的轨迹为椭圆,研究曲线的对称性,并求椭圆的焦点坐标.
解:(1)由题意圆的半径,
故圆的方程为. ………………2分
由得,,将代入
得()为曲线的方程.
(未写范围不扣分)…………4分
(2)由
得,,
所以,同理 ( http: / / www.21cnjy.com ). ……………6分
由题意知 ,所以四边形的面积.
( http: / / www.21cnjy.com )
∵ ,∴ . …………8分
当且仅当时等号成立,此时.
∴ 当时,四边形的面积最大值为. ………………10分
(3) 曲线的方程为(),它关于直线、和原点对称,………11分
下面证明:
设曲线上任一点的坐标为,则,点关于直线的对称点为,显然,所以点在曲线上,故曲线关于直线对称,
同理曲线关于直线和原点对称. ………12分
证明:求得和直线的交点坐标为,
和直线的交点坐标为,
,,,.
在上取点 .
设为曲线上任一点,则
(因为)
.
即曲线上任一点到两定点的距离之和为定值.
若点到两定点的距离之和为定值,可以求得点的轨迹方程为(过程略).
故曲线是椭圆,其焦点坐标为. ………………18分
h
4
2
5
主视图
俯视图
左视图
样本数据
频率
组距
P
N
B
A
D
M
C
第19题图
图(1)
x
y
O
A
B
C
D
图(2)
E
·
F
同课章节目录
