九年级上册人教版数学 24.2 点和圆、直线和圆的位置关系练习题(含答案)
文档属性
| 名称 | 九年级上册人教版数学 24.2 点和圆、直线和圆的位置关系练习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 20:41:21 | ||
图片预览



文档简介
九年级上册人教版数学第二十四章《圆》第2节:点和圆、直线和圆的位置关系练习题
一、单选题
1.在平面直角坐标系中,已知点 ,若以原点O为圆心、5为半径画圆,则点 P与的位置关系是( )
A.点P在上 B.点P在外
C.点P在内 D.无法确定
2.已知的半径为,点P在外,则可能等于( )
A. B. C. D.
3.如图,在已知的中,按以下步骤作图:①分别以为圆心,以大于长为半径作弧,两弧相交于两点;②作直线交于点,连接.若,,则下列结论中错误的是( )
A. B.
C. D.点是的外心
4.如图,,,,,则外心的坐标为( )
A. B. C. D.
5.已知圆心到直线的距离为,的半径为,若、是方程的两个根,则直线和的位置关系是( )
A.相切 B.相离 C.相交 D.相离或相交
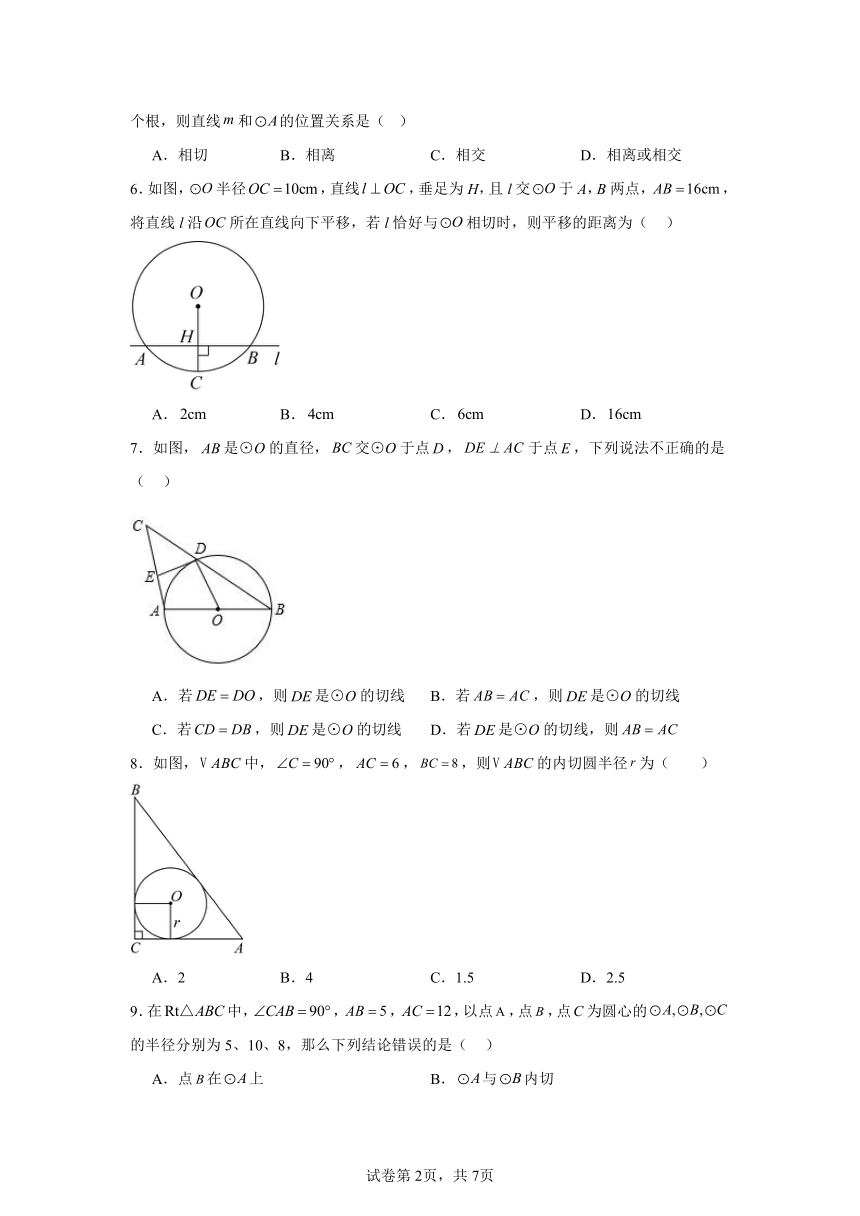
6.如图,半径,直线,垂足为H,且l交于A,B两点,,将直线l沿所在直线向下平移,若l恰好与相切时,则平移的距离为( )
A. B. C. D.
7.如图,是⊙O的直径,交⊙O于点,于点,下列说法不正确的是( )
A.若,则是⊙O的切线 B.若,则是⊙O的切线
C.若,则是⊙O的切线 D.若是⊙O的切线,则
8.如图,中,,,,则的内切圆半径为( )
A.2 B.4 C.1.5 D.2.5
9.在中,,,,以点,点,点为圆心的的半径分别为5、10、8,那么下列结论错误的是( )
A.点在上 B.与内切
C.与有两个公共点 D.直线与相切
10.如图,点是外任意一点,、分别是的切线,、是切点.设与交于点.则点是的( )
A.垂心 B.重心 C.内心 D.外心
二、填空题
11.半径为6的是锐角三角形的外接圆,,连接,,延长交弦于点D,若是直角三角形,则弦的长为 .
12.在中,,,,点D,E,F分别是,,的中点,则的外接圆半径为 .
13.若的半径为,圆心的坐标是,点的坐标是,那么点在 (填“圆内”“圆上”或“圆外”).
14.反证法证明“一个三角形中最多有一个角是直角”时,首先要假设 : .
15.如图,,半径为3的与的两边相切,点P是上任意一点,过点P向的两边作垂线,垂足分别是E、F.设,则p的取值范围是 .
16.如图,的内切圆与,,分别相切于点,,,连接,,,,,则阴影部分的面积为 .
17.如果大圆半径是小圆半径的2倍,当两圆内切时,圆心距为5cm, 那么这两圆外切时,圆心距是 cm.
18.已知一个等腰直角三角形, ,,分别以A,B为圆心,以a的长为半径作圆,两圆的交点为点D,若的长度为2,则的长为 .
三、解答题
19.设的半径为2,点P到圆心的距离,且m使关于x的方程有两个不相等的实数根,试确定点P与的位置关系.
20.如图,在中,,.
(1)作的外接圆(只需作出图形,并保留作图痕迹)
(2)求它的外接圆的面积.
21.如图,在中,,,是的外接圆.
(1)求的半径;
(2)若在同一平面内的也经过B、C两点,且,请直接写出的半径的长.
22.如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,
(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
23.如图,四边形内接于,是的直径,平分,于点E.
(1)判断直线与的位置关系,并说明理由;
(2)若,,求直径的长.
24.如图,为的内切圆,切点分别为,点分别为上的点,且为的切线.
(1)若,求的度数;
(2)若,求的周长.
25.如图,在中,,以为直径的分别与交于点,过点作,垂足为点.
(1)求证:直线是的切线;
(2)求证:;
(3)若的半径为4,,求阴影部分的面积.
26.如图,是的外接圆,为直径,是上一点,且,交的延长线于点.
(1)求证:;
(2)求证:是的切线;
(3)若,,求的半径长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 A D C C D B A A D C
11.或
12.
13.圆内
14.一个三角形中至少有两个内角是直角
15.
16.
17.15
18.或
19.解:∵m使关于x的方程有两个不相等的实数根,
∴,
解得:,
∵圆的半径为2,
∴点P在内.
20.(1)解:如图所示:即为所求的的外接圆;
(2)解:∵,,
∴,
∵,
∴,
∴圆的面积为:.
21.(1)过点作,垂足为,连接、,
,,
垂直平分,
,
点在的垂直平分线上,即在上,
,
,
在中,,,
,
设,则.
在中,,
,即.
解得,
即的半径为;
(2)当也经过、两点,且,如图:
设,
∵,则或,
∵,
或.
∴的半径的长为或.
22.解:(1)证明:∵∠APC和∠ABC是同弧所对的圆周角,∴∠APC=∠ABC.
又∵在△ABC中,∠BAC=∠APC=60°,∴∠ABC=60°.
∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣60°﹣60°=60°.
∴△ABC是等边三角形.
(2)连接OB,
∵△ABC为等边三角形,⊙O为其外接圆,
∴O为△ABC的外心.
∴BO平分∠ABC.∴∠OBD=30°.∴OD=8×=4.
(1)根据同弧所对的圆周角相等的性质和已知∠BAC=∠APC=60°可得△ABC的每一个内角都等于60°,从而得证.
(2)根据等边三角形三线合一的性质,得含30度角直角三角形OBD,从而根据30度角所对边是斜边一半的性质,得OD=8×=4
23.(1)解:直线与相切,
理由:连接,,
平分,
,
,
,
,
,
,
,
是的直径,
,
,
,
,
是的半径,
与相切;
(2)解:设,交于,
,
四边形是矩形,
,
,
,
,
故直径的长为.
24.(1)解:∵,
∴,
∵为的内切圆,
∴,,
∴,
∴;
(2)∵为的内切圆,为的切线,设切点为,
∴,,
∴的周长为:
∵,,,
∴
.
25.解:(1)如图所示,连接,
∵,
∴,
而,
∴,
∵,
∴,
∴,
∴,
∴直线是的切线;
(2)连接,则,则,
则,
∵,,
∴,
而,
∴,
∴,即;
(3)连接,
∵,
∴,
∴,
,
26.(1)
证明:连接
,
,,
四边形是圆内接四边形,
,且,
;
(2)
证明:连接
为直径,
,
又,
,
,
,
,
,
,
是的半径,
是的切线.
(3)
解:过点作于点,
又,,
,
在和中,
(AAS),
,
设,则,
在中,由勾股定理得,,
解得,,
的半径的长为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.在平面直角坐标系中,已知点 ,若以原点O为圆心、5为半径画圆,则点 P与的位置关系是( )
A.点P在上 B.点P在外
C.点P在内 D.无法确定
2.已知的半径为,点P在外,则可能等于( )
A. B. C. D.
3.如图,在已知的中,按以下步骤作图:①分别以为圆心,以大于长为半径作弧,两弧相交于两点;②作直线交于点,连接.若,,则下列结论中错误的是( )
A. B.
C. D.点是的外心
4.如图,,,,,则外心的坐标为( )
A. B. C. D.
5.已知圆心到直线的距离为,的半径为,若、是方程的两个根,则直线和的位置关系是( )
A.相切 B.相离 C.相交 D.相离或相交
6.如图,半径,直线,垂足为H,且l交于A,B两点,,将直线l沿所在直线向下平移,若l恰好与相切时,则平移的距离为( )
A. B. C. D.
7.如图,是⊙O的直径,交⊙O于点,于点,下列说法不正确的是( )
A.若,则是⊙O的切线 B.若,则是⊙O的切线
C.若,则是⊙O的切线 D.若是⊙O的切线,则
8.如图,中,,,,则的内切圆半径为( )
A.2 B.4 C.1.5 D.2.5
9.在中,,,,以点,点,点为圆心的的半径分别为5、10、8,那么下列结论错误的是( )
A.点在上 B.与内切
C.与有两个公共点 D.直线与相切
10.如图,点是外任意一点,、分别是的切线,、是切点.设与交于点.则点是的( )
A.垂心 B.重心 C.内心 D.外心
二、填空题
11.半径为6的是锐角三角形的外接圆,,连接,,延长交弦于点D,若是直角三角形,则弦的长为 .
12.在中,,,,点D,E,F分别是,,的中点,则的外接圆半径为 .
13.若的半径为,圆心的坐标是,点的坐标是,那么点在 (填“圆内”“圆上”或“圆外”).
14.反证法证明“一个三角形中最多有一个角是直角”时,首先要假设 : .
15.如图,,半径为3的与的两边相切,点P是上任意一点,过点P向的两边作垂线,垂足分别是E、F.设,则p的取值范围是 .
16.如图,的内切圆与,,分别相切于点,,,连接,,,,,则阴影部分的面积为 .
17.如果大圆半径是小圆半径的2倍,当两圆内切时,圆心距为5cm, 那么这两圆外切时,圆心距是 cm.
18.已知一个等腰直角三角形, ,,分别以A,B为圆心,以a的长为半径作圆,两圆的交点为点D,若的长度为2,则的长为 .
三、解答题
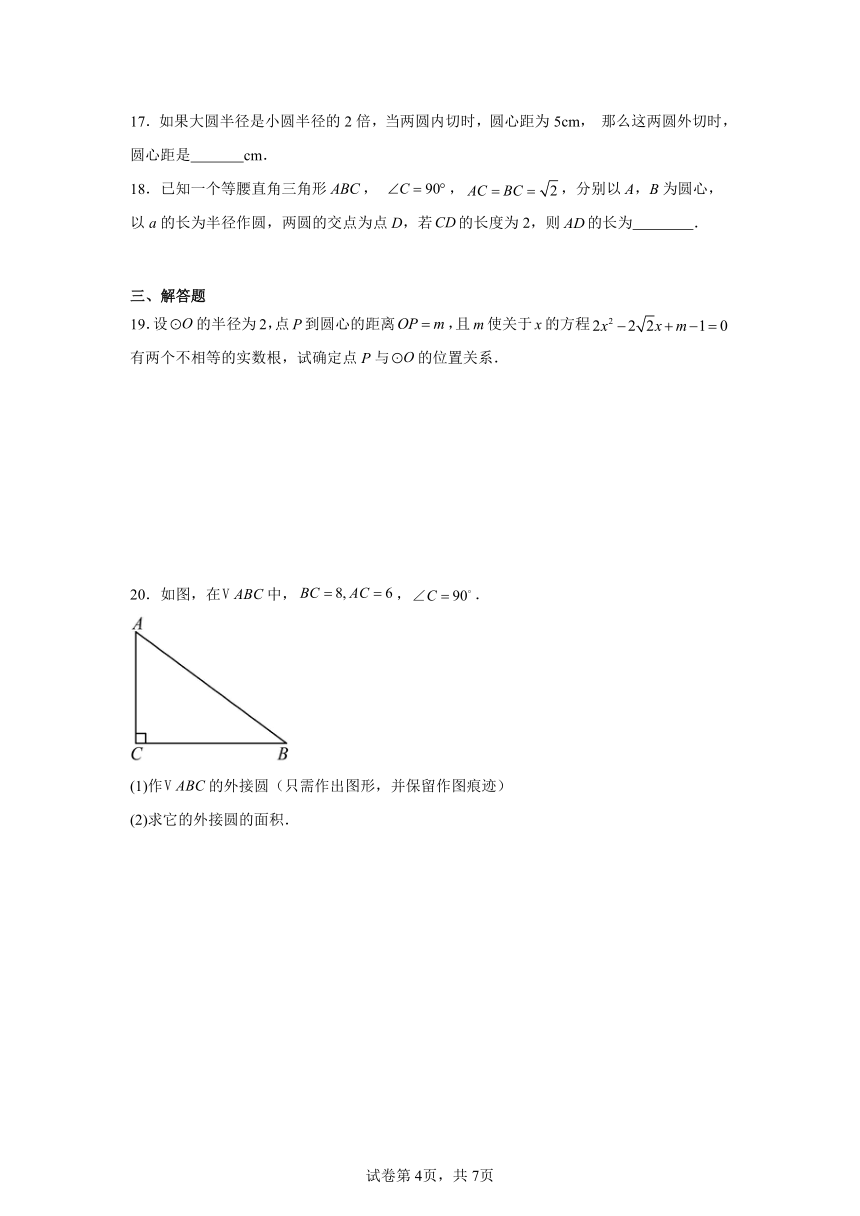
19.设的半径为2,点P到圆心的距离,且m使关于x的方程有两个不相等的实数根,试确定点P与的位置关系.
20.如图,在中,,.
(1)作的外接圆(只需作出图形,并保留作图痕迹)
(2)求它的外接圆的面积.
21.如图,在中,,,是的外接圆.
(1)求的半径;
(2)若在同一平面内的也经过B、C两点,且,请直接写出的半径的长.
22.如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,
(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
23.如图,四边形内接于,是的直径,平分,于点E.
(1)判断直线与的位置关系,并说明理由;
(2)若,,求直径的长.
24.如图,为的内切圆,切点分别为,点分别为上的点,且为的切线.
(1)若,求的度数;
(2)若,求的周长.
25.如图,在中,,以为直径的分别与交于点,过点作,垂足为点.
(1)求证:直线是的切线;
(2)求证:;
(3)若的半径为4,,求阴影部分的面积.
26.如图,是的外接圆,为直径,是上一点,且,交的延长线于点.
(1)求证:;
(2)求证:是的切线;
(3)若,,求的半径长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 A D C C D B A A D C
11.或
12.
13.圆内
14.一个三角形中至少有两个内角是直角
15.
16.
17.15
18.或
19.解:∵m使关于x的方程有两个不相等的实数根,
∴,
解得:,
∵圆的半径为2,
∴点P在内.
20.(1)解:如图所示:即为所求的的外接圆;
(2)解:∵,,
∴,
∵,
∴,
∴圆的面积为:.
21.(1)过点作,垂足为,连接、,
,,
垂直平分,
,
点在的垂直平分线上,即在上,
,
,
在中,,,
,
设,则.
在中,,
,即.
解得,
即的半径为;
(2)当也经过、两点,且,如图:
设,
∵,则或,
∵,
或.
∴的半径的长为或.
22.解:(1)证明:∵∠APC和∠ABC是同弧所对的圆周角,∴∠APC=∠ABC.
又∵在△ABC中,∠BAC=∠APC=60°,∴∠ABC=60°.
∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣60°﹣60°=60°.
∴△ABC是等边三角形.
(2)连接OB,
∵△ABC为等边三角形,⊙O为其外接圆,
∴O为△ABC的外心.
∴BO平分∠ABC.∴∠OBD=30°.∴OD=8×=4.
(1)根据同弧所对的圆周角相等的性质和已知∠BAC=∠APC=60°可得△ABC的每一个内角都等于60°,从而得证.
(2)根据等边三角形三线合一的性质,得含30度角直角三角形OBD,从而根据30度角所对边是斜边一半的性质,得OD=8×=4
23.(1)解:直线与相切,
理由:连接,,
平分,
,
,
,
,
,
,
,
是的直径,
,
,
,
,
是的半径,
与相切;
(2)解:设,交于,
,
四边形是矩形,
,
,
,
,
故直径的长为.
24.(1)解:∵,
∴,
∵为的内切圆,
∴,,
∴,
∴;
(2)∵为的内切圆,为的切线,设切点为,
∴,,
∴的周长为:
∵,,,
∴
.
25.解:(1)如图所示,连接,
∵,
∴,
而,
∴,
∵,
∴,
∴,
∴,
∴直线是的切线;
(2)连接,则,则,
则,
∵,,
∴,
而,
∴,
∴,即;
(3)连接,
∵,
∴,
∴,
,
26.(1)
证明:连接
,
,,
四边形是圆内接四边形,
,且,
;
(2)
证明:连接
为直径,
,
又,
,
,
,
,
,
,
是的半径,
是的切线.
(3)
解:过点作于点,
又,,
,
在和中,
(AAS),
,
设,则,
在中,由勾股定理得,,
解得,,
的半径的长为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
