第四章 数列章末小结复习课 课件(共36张PPT)
文档属性
| 名称 | 第四章 数列章末小结复习课 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-07 12:31:22 | ||
图片预览











文档简介
(共36张PPT)
第三章 圆锥曲线的方程章末复习小结
人教A版(2019)
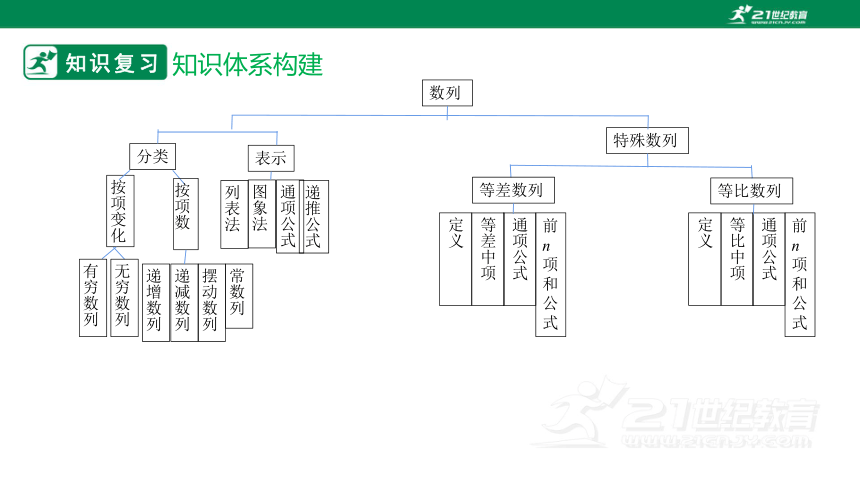
知识复习
知识体系构建
按项变化
数列
特殊数列
表示
分类
无穷数列
有穷数列
按项数
递增数列
递减数列
摆动数列
常数列
列表法
图象法
通项公式
递推公式
等差数列
等比数列
定义
等差中项
通项公式
前n项和公式
定义
等比中项
通项公式
前n项和公式
知识梳理
等差数列
1.等差数列的概念
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列. 这个常数叫做等差数列的公差通常用字母d表示.
2.等差中项
等差数列的符号语言:an-an-1 = d (d是常数,n≥2,)
由三个数a,A,b组成的等差数列可以看成是最简单的等差数列.这时,A叫做a与b的等差中项.
2A=a+b或A=.
3.等差数列的通项公式
an=a1+(n-1)d.
首项为a1,公差为d的等差数列{an}的通项公式为
d>0时,{an}是递增数列;d<0时,{an}是递减数列;d=0时,{an}是常数列.
知识梳理
等差数列
已知是等差数列,公差为,
⑴{an}中每隔相同的项抽出来的项按照原来的顺序排列,构成的新数列仍然是等差数列.即,…()是公差为md的等差数列.
⑵数列(b为常数,b≠0)是公差为bd的等差数列;
⑷{ban+c}(b,c是常数)是公差为bd的等差数列.
⑸若{an},{bn}分别是公差为d1,d2的等差数列,则数列{pan+qbn}(p,q是常数)是公差为pd1+qd2的等差数列.
⑶{c+an}(c为任一常数)是公差为d的等差数列;
4.等差数列的性质
⑹若数列{an}是等差数列,p , q , s , t∈N*,且p+q=s+t.则ap+aq=as+at.
知识梳理
等差数列
5.等差数列的前n项和公式
.
.
⑶若S奇表示奇数项的和,S偶表示偶数项的和,公差为d.
⑵数列{an}是等差数列 Sn=an2+bn(a,b为常数) 数列{}为等差数列;
当项数为偶数2n时,S偶-S奇=nd,;
当项数为奇数2n-1时,S奇-S偶=an,.
⑴等差数列的依次k项之和,Sk,S2k-Sk,S3k-S2k,…组成公差为k2d的等差数列;
知识梳理
等比数列
等比数列
定义
符号表示
公比
通项公式
等比中项
等比数列前n项和公式
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列
(n≥2,).
().
an=a1qn-1.
.
公比q可正、可负但不可为零
G是a与b的等比中项 G2=ab(ab>0).
.
知识梳理
等比数列
等比数列的性质
⑴若数列{an},{bn}是项数相同的等比数列,则{an·bn}也是等比数列.特别地,若{an}是等比数列,c是不等于0的常数,则{c·an}也是等比数列.
⑵在等比数列{an}中,若m+n=p+q,则aman=apaq.
⑶若等比数列{an}是有穷数列,则与首末两项等距离的两项的积相等,且等于首末两项的积.
⑷在等比数列{an}中,每隔k项取出一项,按原来的顺序排列,所得新数列仍为等比数列,公比为qk+1.
⑸在等比数列{an}中,当m,n,p(m,n,p∈N*)成等差数列时,am,an,ap成等比数列.
⑹若等比数列{an}的公比q≠-1,前n项和为Sn.则Sn,S2n-Sn,S3n-S2n成等比数列,公比为qn.
⑺若等比数列{an}的公比为q,则(m,n∈N ).
题型探究
题型1:等差与等比数列的基本运算
1.在等差数列和等比数列的通项公式an与前n项和公式Sn中,共涉及五个量:a1,an,n,d(或q),Sn,其中a1和d(或q)为基本量,“知三求二”是指将已知条件转换成关于a1,d(q),an,Sn,n的方程组,利用方程思想求出需要的量,当然在求解中若能运用等差(比)数列的性质会更好,这样可以化繁为简,减少运算量,同时还要注意整体代入思想方法的运用.
2.数列的基本运算以小题居多,但也可作为解答题第一步命题,主要考查利用数列的通项公式及求和公式,求数列中的项、公差、公比及前n项和等,一般试题难度较小.
3.通过等差、等比数列的基本运算,培养数学运算、逻辑推理等核心素养.
题型探究
【例1】等比数列{an}中,已知a1=2,a4=16.
⑴求数列{an}的通项公式;
⑵若a3,a5分别为等差数列{bn}的第3项和第5项,试求数列{bn}的通项公式及前n项和Sn.
解:
⑴设{an}的公比为q,由已知得16=2q3,
∴an=2×2n-1=2n.
题型1:等差与等比数列的基本运算
解得q=2,
⑵由⑴得a3=8,a5=32,则
b3=8,b5=32.
设{bn}的公差为d,则有
,
解得,
∴bn=-16+12(n-1)=12n-28.
∴数列{bn}的前n项和Sn=.
初试身手
1.⑴记Sn为等差数列{an}的前n项和.若a2+a6=10,a4a8=45,则S5=( )
A.25 B.22 C.20 D.15
⑵已知等差数列{an}的公差不为0,若a1,a3,a6成等比数列,则这个等比数列的公比是( )
A. B. C.2 D.4
解:
⑴方法1:由a2+a6=10,可得2a4=10,即a4=5,
设等差数列{an}的公差为d,则d==1,
又a4=5,∴a1=2,
又a4a8=45, ∴a8=9.
∴S5=5a1+×d=20,故选C.
初试身手
1.⑴记Sn为等差数列{an}的前n项和.若a2+a6=10,a4a8=45,则S5=( )
A.25 B.22 C.20 D.15
⑵已知等差数列{an}的公差不为0,若a1,a3,a6成等比数列,则这个等比数列的公比是( )
A. B. C.2 D.4
解:
由①②可得a1=2,d=1,
∴S5=5a1+×d=20,故选C.
⑴方法2:设等差数列{an}的公差为d,则可得a1+3d=5,①
由a4a8=45,可得(a1+3d)·(a1+7d)=45,②
C
初试身手
1.⑴记Sn为等差数列{an}的前n项和.若a2+a6=10,a4a8=45,则S5=( )
A.25 B.22 C.20 D.15
⑵已知等差数列{an}的公差不为0,若a1,a3,a6成等比数列,则这个等比数列的公比是( )
A. B. C.2 D.4
解:
∴,即(a1+2d)2=a1(a1+5d),
化简整理,得a1d-4d 2=0,即d(a1-4d)=0,
⑵由题意,设等差数列{an}的公差为d(d≠0),则a3=a1+2d,a6=a1+5d,
∵a1,a3,a6成等比数列,
B
∵d≠0,
∴a1-4d=0,即a1=4d,
∴等比数列的公比为.故选B.
题型探究
题型2:等差、等比数列的判定与证明
等差数列、等比数列的判断方法
⑴定义法:an+1-an=d(常数) {an}是等差数列;
=q(q为常数,q≠0) {an}是等比数列.
⑵中项公式法:2an+1=an+an+2 {an}是等差数列;
=an·an+2(an≠0) {an}是等比数列.
⑶通项公式法:an=kn+b(k,b是常数) {an}是等差数列;
an=c·qn(c,q为非零常数) {an}是等比数列.
⑷前n项和公式法:Sn=An2+Bn(A,B为常数,n∈N*) {an}是等差数列;
Sn=Aqn-A(A,q为常数,且A≠0,q≠0,q≠1,n∈N*) {an}是等比数列.
题型探究
【例2】已知数列{an}、{bn}满足:a1=1,a2=a(a为常数),且bn=an·an+1,其中n=1,2,3,….
⑴ 若{an}是等比数列,试求数列{bn}的前n项和Sn的公式;
⑵当{bn}是等比数列时,甲同学说:{an}一定是等比数列;乙同学说:{an}一定不是等比数列.你认为他们的说法是否正确?为什么?
解:
⑴∵{an}是等比数列,a1=1,a2=a(a为常数),
∴a≠0,an=an-1.
又bn=an·an+1,
题型2:等差、等比数列的判定与证明
∴b1=a1·a2=a,,
∴数列{bn}是以a为首项,a2为公比的等比数列.
∴Sn=.
题型探究
【例2】已知数列{an}、{bn}满足:a1=1,a2=a(a为常数),且bn=an·an+1,其中n=1,2,3,….
⑴ 若{an}是等比数列,试求数列{bn}的前n项和Sn的公式;
⑵当{bn}是等比数列时,甲同学说:{an}一定是等比数列;乙同学说:{an}一定不是等比数列.你认为他们的说法是否正确?为什么?
解:
⑵甲、乙两个同学说法都不正确,理由如下:
方法1:设{bn}的公比为q,则,且a≠0,
又a1=1,a2=a,a1,a3,a5,…,a2n-1,…是以1为首项,q为公比的等比数列;a2,a4,a6,…,a2n,…是以a为首项,q为公比的等比数列.
题型2:等差、等比数列的判定与证明
即{an}为:1,a,q,aq,q2,aq2,…,
∴当q=a2时,{an}是等比数列;当q≠a2时,{an}不是等比数列.
题型探究
【例2】已知数列{an}、{bn}满足:a1=1,a2=a(a为常数),且bn=an·an+1,其中n=1,2,3,….
⑴ 若{an}是等比数列,试求数列{bn}的前n项和Sn的公式;
⑵当{bn}是等比数列时,甲同学说:{an}一定是等比数列;乙同学说:{an}一定不是等比数列.你认为他们的说法是否正确?为什么?
解:
⑵甲、乙两个同学说法都不正确,理由如下:
方法2:{an}可能是等比数列,也可能不是等比数列,举例说明如下:
设{bn}的公比为q,
题型2:等差、等比数列的判定与证明
①取a=q=1时,an=1(n∈N*),
此时bn=anan+1=1,{an}、{bn}都是等比数列.
②取a=2,q=1时,an=,bn=2(n∈N*).
此时{bn}是等比数列,{an}不是等比数列.
初试身手
2.已知数列{an}的前n项和为Sn,且an+Sn=n.
⑴设cn=an-1,求证:{cn}是等比数列;
⑵求数列{an}的通项公式.
解:
⑴证明:∵an+Sn=n,∴an+1+Sn+1=n+1,
两式相减,得an+1-an+an+1=1,
整理,得an+1-1=(an-1),
又∵cn=an-1,
∴cn+1=cn,
又∵a1+a1=1,即a1=,
∴c1=a1-1=-1=-,
∴数列{cn}是以-为首项,为公比的等比数列.
⑵由⑴可知,cn=an-1=,
∴an=1-.
题型探究
题型3:数列的通项
数列通项的求法
1.定义法:直接利用等差数列或等比数列的定义求通项的方法,这种方法适用于已知数列类型的题目.
2.已知Sn求an:若已知数列的前n项和Sn与an的关系,求数列的通项an可用公式an=求解.
3.由递推公式求数列通项:对于递推公式确定的数列的求解,通常可以通过递推公式的变换,转化为等差数列或等比数列问题,有时也用到一些特殊的转化方法与特殊数列.
题型探究
题型3:数列的通项
4.累加法:适用形如“an+1-an=f(n)”,an=a1+(a2-a1)+(a3-a2)+…+(an-an-1).
5.累乘法:适用于形如“=f(n)”,an=a1···…·.
6.构造法:①形如“an=kan-1+b(k,b为常数,k≠0,k≠1,n≥2,n∈N*)”,可令an+t=k(an-1+t),结合已知条件可得t=,构造等比数列.
②取倒数法:形如“an=(n≥2,n∈N*,k,m,p均为常数,m≠0)”,可在等式两边取倒数,转化为等差数列或转化为类型①.
题型探究
【例3】⑴已知数列{an}的前n项和Sn=3+2n,求an.
⑵数列{an}的前n项和为Sn且a1=1,an+1=Sn,求an.
题型3:数列的通项
解:
⑴当n≥2时,an=Sn-Sn-1=3+2n-(3+2n-1)=2n-1,
当n=1时,a1=S1=5不适合上式.
∴.
⑵∵Sn=3an+1, ①
∴n≥2时,Sn-1=3an.②
①-②得Sn-Sn-1=3an+1-3an,
∴3an+1=4an,即,
又a2=.
∴n≥2时,an=,不适合a1=1.
∴an=.
初试身手
解:
3.⑴设数列{an}是首项为1的正项数列,且an+1-an+an+1·an=0(n∈N*),求{an}的通项公式.
⑵已知数列{an}中,a1=1,且an+1-an=3n-n,求数列{an}的通项公式.
∴{}是首项为1,公差为1的等差数列.
又∵a1=1,
∴=n,即an=.
⑴∵an+1-an+an+1·an=0
∴
初试身手
解:
3.⑴设数列{an}是首项为1的正项数列,且an+1-an+an+1·an=0(n∈N*),求{an}的通项公式.
⑵已知数列{an}中,a1=1,且an+1-an=3n-n,求数列{an}的通项公式.
当n≥2时,以上n-1个等式两端分别相加,得
an-1-an-2=3n-2-(n-2),
a3-a2=32-2,a2-a1=3-1.
…,
(an-an-1)+(an-1-an-2)+…+(a2-a1)
=3n-1+3n-2+…+3-[(n-1)+(n-2)+…+1],
⑵由an+1-an=3n-n,得
an-an-1=3n-1-(n-1),
初试身手
解:
3.⑴设数列{an}是首项为1的正项数列,且an+1-an+an+1·an=0(n∈N*),求{an}的通项公式.
⑵已知数列{an}中,a1=1,且an+1-an=3n-n,求数列{an}的通项公式.
∴an=.
=3n-1+3n-2+…+3-[(n-1)+(n-2)+…+1],
又∵a1=1,
即an-a1=,
显然a1=1也适合上式,
∴{an}的通项公式为an=.
⑵当n≥2时,以上n-1个等式两端分别相加,得
(an-an-1)+(an-1-an-2)+…+(a2-a1)
题型探究
题型4:数列求和
一般常见的求和方法有:
1.公式法(直接利用等差或等比数列的前n项和公式);
2.分组求和法;
3.错位相减法;
4.倒序相加法;
5.裂项相消法.把数列的通项拆成两项之差,在求和时中间的一些项可以相互抵消,从而求得其和.
6.并项求和法.一个数列的前n项和中,可两两结合求解,则称之为并项求和.形如an=(-1)nf(n)类型,可采用两项合并求解.
题型探究
【例4】已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数且k≠0,c≠1),且a2=4,a6=8a3,
⑴求an;
⑵求数列{nan}的前n项和Tn.
题型4:数列求和
解:
⑴当n>1时,an=Sn-Sn-1=k(cn-cn-1),
则a6=k(c6-c5),a3=k(c3-c2),
又∵a2=4,即k(c2-c1)=4,
∵k≠0,c≠1,
∴8,即c=2,
解得k=2,
∴an=2n.
当n=1时,a1=S1=2.
综上所述,an=2n(n∈N*).
题型探究
【例4】已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数且k≠0,c≠1),且a2=4,a6=8a3,
⑴求an;
⑵求数列{nan}的前n项和Tn.
题型4:数列求和
解:
⑵由⑴得nan=n·2n,
则Tn=2+2·22+3·23+…+n·2n,
∴2Tn=1·22+2·23+3·24+…+(n-1)·2n+n·2n+1,
两式作差,得
-Tn=2+22+23+…+2n-n·2n+1=,
∴Tn=2+(n-1)·2n+1.
初试身手
解:
4.已知各项均为正数的数列{an}满足a1=1,当n≥2时=n(n-1).
⑴求证:数列等差数列;
⑵求数列{an}的通项公式;
⑶设bn=,求数列{bn}的前n项和Tn.
⑴证明:当n≥2时=n(n-1),
又∵a1=1,
⑵由⑴知=1+n-1=n,
整理得=1,
∴数列是以1为首项,1为公差的等差数列.
又∵an>0,
∴an=n..
∴=n2,
初试身手
解:
4.已知各项均为正数的数列{an}满足a1=1,当n≥2时=n(n-1).
⑴求证:数列等差数列;
⑵求数列{an}的通项公式;
⑶设bn=,求数列{bn}的前n项和Tn.
⑶由⑵得bn=,
Tn=1×+2×+3×+…+n,②
①-②得
∴Tn=1×2×3×…+n,①
Tn=-n=1-.
∴Tn=2-.
题型探究
【例5】我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数x的不足近似值和过剩近似值分别为和(a,b,c,d∈N*),则是x的更为精确的不足近似值或过剩近似值.我们知道=2.236 067 …,令<<,则第一次用“调日法”后得是的更为精确的过剩近似值,即<<,记a1=.若每次都取最简分数,继续使用“调日法”,将用“调日法”得到的的一列近似分数记为数列{an},则a5= .
题型5:数列的综合应用与创新问题
第一次用“调日法”后,得
a1=;
a2=,
则第二次用“调日法”后得;
解:
a3=.
题型探究
【例5】我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数x的不足近似值和过剩近似值分别为和(a,b,c,d∈N*),则是x的更为精确的不足近似值或过剩近似值.我们知道=2.236 067 …,令<<,则第一次用“调日法”后得是的更为精确的过剩近似值,即<<,记a1=.若每次都取最简分数,继续使用“调日法”,将用“调日法”得到的的一列近似分数记为数列{an},则a5= .
题型5:数列的综合应用与创新问题
则第三次用“调日法”后,得;
a4=,
则第四次用“调日法”后,得;
解:
a5=.
初试身手
5.分形几何学又被称为“大自然的几何学”,是一门以不规则几何形态为研究对象的几何学.一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统,简单的说,分形就是研究无限复杂具备相似结构的几何学.下面用分形的方法得到一系列图形,如图1,正三角形的边长为1,在各边取两个三等分点,往外再作一个正三角形,得到图2中的图形;对图2中的各边做相同的操作,得到图3中的图形;以此类推,就得到了以下一系列图形,记第n个图形(图1为第一个图形)中的所有外围线段长的和为cn,则满足c1+c2+c3+…+cn>81的最小正整数n的值为________.(参考数据:lg 2≈0.301 0,lg 3≈0.477 1)
初试身手
解:
设第n个图形中线段的长度为an,则an=,
设第n个图形中线段的条数为bn,则bn=3×4n-1,
∴cn=anbn=3×,
则c1+c2+c3+…+cn=9×,
由题意知每个图形中每条线段的长度相等.
令9×>81,得>10,
则n>≈8.006,
即满足不等式的最小正整数n的值为9.
作业布置
作业: p54-56 复习参考题4 第3,5,6,7,11,12题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第三章 圆锥曲线的方程章末复习小结
人教A版(2019)
知识复习
知识体系构建
按项变化
数列
特殊数列
表示
分类
无穷数列
有穷数列
按项数
递增数列
递减数列
摆动数列
常数列
列表法
图象法
通项公式
递推公式
等差数列
等比数列
定义
等差中项
通项公式
前n项和公式
定义
等比中项
通项公式
前n项和公式
知识梳理
等差数列
1.等差数列的概念
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列. 这个常数叫做等差数列的公差通常用字母d表示.
2.等差中项
等差数列的符号语言:an-an-1 = d (d是常数,n≥2,)
由三个数a,A,b组成的等差数列可以看成是最简单的等差数列.这时,A叫做a与b的等差中项.
2A=a+b或A=.
3.等差数列的通项公式
an=a1+(n-1)d.
首项为a1,公差为d的等差数列{an}的通项公式为
d>0时,{an}是递增数列;d<0时,{an}是递减数列;d=0时,{an}是常数列.
知识梳理
等差数列
已知是等差数列,公差为,
⑴{an}中每隔相同的项抽出来的项按照原来的顺序排列,构成的新数列仍然是等差数列.即,…()是公差为md的等差数列.
⑵数列(b为常数,b≠0)是公差为bd的等差数列;
⑷{ban+c}(b,c是常数)是公差为bd的等差数列.
⑸若{an},{bn}分别是公差为d1,d2的等差数列,则数列{pan+qbn}(p,q是常数)是公差为pd1+qd2的等差数列.
⑶{c+an}(c为任一常数)是公差为d的等差数列;
4.等差数列的性质
⑹若数列{an}是等差数列,p , q , s , t∈N*,且p+q=s+t.则ap+aq=as+at.
知识梳理
等差数列
5.等差数列的前n项和公式
.
.
⑶若S奇表示奇数项的和,S偶表示偶数项的和,公差为d.
⑵数列{an}是等差数列 Sn=an2+bn(a,b为常数) 数列{}为等差数列;
当项数为偶数2n时,S偶-S奇=nd,;
当项数为奇数2n-1时,S奇-S偶=an,.
⑴等差数列的依次k项之和,Sk,S2k-Sk,S3k-S2k,…组成公差为k2d的等差数列;
知识梳理
等比数列
等比数列
定义
符号表示
公比
通项公式
等比中项
等比数列前n项和公式
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列
(n≥2,).
().
an=a1qn-1.
.
公比q可正、可负但不可为零
G是a与b的等比中项 G2=ab(ab>0).
.
知识梳理
等比数列
等比数列的性质
⑴若数列{an},{bn}是项数相同的等比数列,则{an·bn}也是等比数列.特别地,若{an}是等比数列,c是不等于0的常数,则{c·an}也是等比数列.
⑵在等比数列{an}中,若m+n=p+q,则aman=apaq.
⑶若等比数列{an}是有穷数列,则与首末两项等距离的两项的积相等,且等于首末两项的积.
⑷在等比数列{an}中,每隔k项取出一项,按原来的顺序排列,所得新数列仍为等比数列,公比为qk+1.
⑸在等比数列{an}中,当m,n,p(m,n,p∈N*)成等差数列时,am,an,ap成等比数列.
⑹若等比数列{an}的公比q≠-1,前n项和为Sn.则Sn,S2n-Sn,S3n-S2n成等比数列,公比为qn.
⑺若等比数列{an}的公比为q,则(m,n∈N ).
题型探究
题型1:等差与等比数列的基本运算
1.在等差数列和等比数列的通项公式an与前n项和公式Sn中,共涉及五个量:a1,an,n,d(或q),Sn,其中a1和d(或q)为基本量,“知三求二”是指将已知条件转换成关于a1,d(q),an,Sn,n的方程组,利用方程思想求出需要的量,当然在求解中若能运用等差(比)数列的性质会更好,这样可以化繁为简,减少运算量,同时还要注意整体代入思想方法的运用.
2.数列的基本运算以小题居多,但也可作为解答题第一步命题,主要考查利用数列的通项公式及求和公式,求数列中的项、公差、公比及前n项和等,一般试题难度较小.
3.通过等差、等比数列的基本运算,培养数学运算、逻辑推理等核心素养.
题型探究
【例1】等比数列{an}中,已知a1=2,a4=16.
⑴求数列{an}的通项公式;
⑵若a3,a5分别为等差数列{bn}的第3项和第5项,试求数列{bn}的通项公式及前n项和Sn.
解:
⑴设{an}的公比为q,由已知得16=2q3,
∴an=2×2n-1=2n.
题型1:等差与等比数列的基本运算
解得q=2,
⑵由⑴得a3=8,a5=32,则
b3=8,b5=32.
设{bn}的公差为d,则有
,
解得,
∴bn=-16+12(n-1)=12n-28.
∴数列{bn}的前n项和Sn=.
初试身手
1.⑴记Sn为等差数列{an}的前n项和.若a2+a6=10,a4a8=45,则S5=( )
A.25 B.22 C.20 D.15
⑵已知等差数列{an}的公差不为0,若a1,a3,a6成等比数列,则这个等比数列的公比是( )
A. B. C.2 D.4
解:
⑴方法1:由a2+a6=10,可得2a4=10,即a4=5,
设等差数列{an}的公差为d,则d==1,
又a4=5,∴a1=2,
又a4a8=45, ∴a8=9.
∴S5=5a1+×d=20,故选C.
初试身手
1.⑴记Sn为等差数列{an}的前n项和.若a2+a6=10,a4a8=45,则S5=( )
A.25 B.22 C.20 D.15
⑵已知等差数列{an}的公差不为0,若a1,a3,a6成等比数列,则这个等比数列的公比是( )
A. B. C.2 D.4
解:
由①②可得a1=2,d=1,
∴S5=5a1+×d=20,故选C.
⑴方法2:设等差数列{an}的公差为d,则可得a1+3d=5,①
由a4a8=45,可得(a1+3d)·(a1+7d)=45,②
C
初试身手
1.⑴记Sn为等差数列{an}的前n项和.若a2+a6=10,a4a8=45,则S5=( )
A.25 B.22 C.20 D.15
⑵已知等差数列{an}的公差不为0,若a1,a3,a6成等比数列,则这个等比数列的公比是( )
A. B. C.2 D.4
解:
∴,即(a1+2d)2=a1(a1+5d),
化简整理,得a1d-4d 2=0,即d(a1-4d)=0,
⑵由题意,设等差数列{an}的公差为d(d≠0),则a3=a1+2d,a6=a1+5d,
∵a1,a3,a6成等比数列,
B
∵d≠0,
∴a1-4d=0,即a1=4d,
∴等比数列的公比为.故选B.
题型探究
题型2:等差、等比数列的判定与证明
等差数列、等比数列的判断方法
⑴定义法:an+1-an=d(常数) {an}是等差数列;
=q(q为常数,q≠0) {an}是等比数列.
⑵中项公式法:2an+1=an+an+2 {an}是等差数列;
=an·an+2(an≠0) {an}是等比数列.
⑶通项公式法:an=kn+b(k,b是常数) {an}是等差数列;
an=c·qn(c,q为非零常数) {an}是等比数列.
⑷前n项和公式法:Sn=An2+Bn(A,B为常数,n∈N*) {an}是等差数列;
Sn=Aqn-A(A,q为常数,且A≠0,q≠0,q≠1,n∈N*) {an}是等比数列.
题型探究
【例2】已知数列{an}、{bn}满足:a1=1,a2=a(a为常数),且bn=an·an+1,其中n=1,2,3,….
⑴ 若{an}是等比数列,试求数列{bn}的前n项和Sn的公式;
⑵当{bn}是等比数列时,甲同学说:{an}一定是等比数列;乙同学说:{an}一定不是等比数列.你认为他们的说法是否正确?为什么?
解:
⑴∵{an}是等比数列,a1=1,a2=a(a为常数),
∴a≠0,an=an-1.
又bn=an·an+1,
题型2:等差、等比数列的判定与证明
∴b1=a1·a2=a,,
∴数列{bn}是以a为首项,a2为公比的等比数列.
∴Sn=.
题型探究
【例2】已知数列{an}、{bn}满足:a1=1,a2=a(a为常数),且bn=an·an+1,其中n=1,2,3,….
⑴ 若{an}是等比数列,试求数列{bn}的前n项和Sn的公式;
⑵当{bn}是等比数列时,甲同学说:{an}一定是等比数列;乙同学说:{an}一定不是等比数列.你认为他们的说法是否正确?为什么?
解:
⑵甲、乙两个同学说法都不正确,理由如下:
方法1:设{bn}的公比为q,则,且a≠0,
又a1=1,a2=a,a1,a3,a5,…,a2n-1,…是以1为首项,q为公比的等比数列;a2,a4,a6,…,a2n,…是以a为首项,q为公比的等比数列.
题型2:等差、等比数列的判定与证明
即{an}为:1,a,q,aq,q2,aq2,…,
∴当q=a2时,{an}是等比数列;当q≠a2时,{an}不是等比数列.
题型探究
【例2】已知数列{an}、{bn}满足:a1=1,a2=a(a为常数),且bn=an·an+1,其中n=1,2,3,….
⑴ 若{an}是等比数列,试求数列{bn}的前n项和Sn的公式;
⑵当{bn}是等比数列时,甲同学说:{an}一定是等比数列;乙同学说:{an}一定不是等比数列.你认为他们的说法是否正确?为什么?
解:
⑵甲、乙两个同学说法都不正确,理由如下:
方法2:{an}可能是等比数列,也可能不是等比数列,举例说明如下:
设{bn}的公比为q,
题型2:等差、等比数列的判定与证明
①取a=q=1时,an=1(n∈N*),
此时bn=anan+1=1,{an}、{bn}都是等比数列.
②取a=2,q=1时,an=,bn=2(n∈N*).
此时{bn}是等比数列,{an}不是等比数列.
初试身手
2.已知数列{an}的前n项和为Sn,且an+Sn=n.
⑴设cn=an-1,求证:{cn}是等比数列;
⑵求数列{an}的通项公式.
解:
⑴证明:∵an+Sn=n,∴an+1+Sn+1=n+1,
两式相减,得an+1-an+an+1=1,
整理,得an+1-1=(an-1),
又∵cn=an-1,
∴cn+1=cn,
又∵a1+a1=1,即a1=,
∴c1=a1-1=-1=-,
∴数列{cn}是以-为首项,为公比的等比数列.
⑵由⑴可知,cn=an-1=,
∴an=1-.
题型探究
题型3:数列的通项
数列通项的求法
1.定义法:直接利用等差数列或等比数列的定义求通项的方法,这种方法适用于已知数列类型的题目.
2.已知Sn求an:若已知数列的前n项和Sn与an的关系,求数列的通项an可用公式an=求解.
3.由递推公式求数列通项:对于递推公式确定的数列的求解,通常可以通过递推公式的变换,转化为等差数列或等比数列问题,有时也用到一些特殊的转化方法与特殊数列.
题型探究
题型3:数列的通项
4.累加法:适用形如“an+1-an=f(n)”,an=a1+(a2-a1)+(a3-a2)+…+(an-an-1).
5.累乘法:适用于形如“=f(n)”,an=a1···…·.
6.构造法:①形如“an=kan-1+b(k,b为常数,k≠0,k≠1,n≥2,n∈N*)”,可令an+t=k(an-1+t),结合已知条件可得t=,构造等比数列.
②取倒数法:形如“an=(n≥2,n∈N*,k,m,p均为常数,m≠0)”,可在等式两边取倒数,转化为等差数列或转化为类型①.
题型探究
【例3】⑴已知数列{an}的前n项和Sn=3+2n,求an.
⑵数列{an}的前n项和为Sn且a1=1,an+1=Sn,求an.
题型3:数列的通项
解:
⑴当n≥2时,an=Sn-Sn-1=3+2n-(3+2n-1)=2n-1,
当n=1时,a1=S1=5不适合上式.
∴.
⑵∵Sn=3an+1, ①
∴n≥2时,Sn-1=3an.②
①-②得Sn-Sn-1=3an+1-3an,
∴3an+1=4an,即,
又a2=.
∴n≥2时,an=,不适合a1=1.
∴an=.
初试身手
解:
3.⑴设数列{an}是首项为1的正项数列,且an+1-an+an+1·an=0(n∈N*),求{an}的通项公式.
⑵已知数列{an}中,a1=1,且an+1-an=3n-n,求数列{an}的通项公式.
∴{}是首项为1,公差为1的等差数列.
又∵a1=1,
∴=n,即an=.
⑴∵an+1-an+an+1·an=0
∴
初试身手
解:
3.⑴设数列{an}是首项为1的正项数列,且an+1-an+an+1·an=0(n∈N*),求{an}的通项公式.
⑵已知数列{an}中,a1=1,且an+1-an=3n-n,求数列{an}的通项公式.
当n≥2时,以上n-1个等式两端分别相加,得
an-1-an-2=3n-2-(n-2),
a3-a2=32-2,a2-a1=3-1.
…,
(an-an-1)+(an-1-an-2)+…+(a2-a1)
=3n-1+3n-2+…+3-[(n-1)+(n-2)+…+1],
⑵由an+1-an=3n-n,得
an-an-1=3n-1-(n-1),
初试身手
解:
3.⑴设数列{an}是首项为1的正项数列,且an+1-an+an+1·an=0(n∈N*),求{an}的通项公式.
⑵已知数列{an}中,a1=1,且an+1-an=3n-n,求数列{an}的通项公式.
∴an=.
=3n-1+3n-2+…+3-[(n-1)+(n-2)+…+1],
又∵a1=1,
即an-a1=,
显然a1=1也适合上式,
∴{an}的通项公式为an=.
⑵当n≥2时,以上n-1个等式两端分别相加,得
(an-an-1)+(an-1-an-2)+…+(a2-a1)
题型探究
题型4:数列求和
一般常见的求和方法有:
1.公式法(直接利用等差或等比数列的前n项和公式);
2.分组求和法;
3.错位相减法;
4.倒序相加法;
5.裂项相消法.把数列的通项拆成两项之差,在求和时中间的一些项可以相互抵消,从而求得其和.
6.并项求和法.一个数列的前n项和中,可两两结合求解,则称之为并项求和.形如an=(-1)nf(n)类型,可采用两项合并求解.
题型探究
【例4】已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数且k≠0,c≠1),且a2=4,a6=8a3,
⑴求an;
⑵求数列{nan}的前n项和Tn.
题型4:数列求和
解:
⑴当n>1时,an=Sn-Sn-1=k(cn-cn-1),
则a6=k(c6-c5),a3=k(c3-c2),
又∵a2=4,即k(c2-c1)=4,
∵k≠0,c≠1,
∴8,即c=2,
解得k=2,
∴an=2n.
当n=1时,a1=S1=2.
综上所述,an=2n(n∈N*).
题型探究
【例4】已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数且k≠0,c≠1),且a2=4,a6=8a3,
⑴求an;
⑵求数列{nan}的前n项和Tn.
题型4:数列求和
解:
⑵由⑴得nan=n·2n,
则Tn=2+2·22+3·23+…+n·2n,
∴2Tn=1·22+2·23+3·24+…+(n-1)·2n+n·2n+1,
两式作差,得
-Tn=2+22+23+…+2n-n·2n+1=,
∴Tn=2+(n-1)·2n+1.
初试身手
解:
4.已知各项均为正数的数列{an}满足a1=1,当n≥2时=n(n-1).
⑴求证:数列等差数列;
⑵求数列{an}的通项公式;
⑶设bn=,求数列{bn}的前n项和Tn.
⑴证明:当n≥2时=n(n-1),
又∵a1=1,
⑵由⑴知=1+n-1=n,
整理得=1,
∴数列是以1为首项,1为公差的等差数列.
又∵an>0,
∴an=n..
∴=n2,
初试身手
解:
4.已知各项均为正数的数列{an}满足a1=1,当n≥2时=n(n-1).
⑴求证:数列等差数列;
⑵求数列{an}的通项公式;
⑶设bn=,求数列{bn}的前n项和Tn.
⑶由⑵得bn=,
Tn=1×+2×+3×+…+n,②
①-②得
∴Tn=1×2×3×…+n,①
Tn=-n=1-.
∴Tn=2-.
题型探究
【例5】我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数x的不足近似值和过剩近似值分别为和(a,b,c,d∈N*),则是x的更为精确的不足近似值或过剩近似值.我们知道=2.236 067 …,令<<,则第一次用“调日法”后得是的更为精确的过剩近似值,即<<,记a1=.若每次都取最简分数,继续使用“调日法”,将用“调日法”得到的的一列近似分数记为数列{an},则a5= .
题型5:数列的综合应用与创新问题
第一次用“调日法”后,得
a1=;
a2=,
则第二次用“调日法”后得;
解:
a3=.
题型探究
【例5】我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数x的不足近似值和过剩近似值分别为和(a,b,c,d∈N*),则是x的更为精确的不足近似值或过剩近似值.我们知道=2.236 067 …,令<<,则第一次用“调日法”后得是的更为精确的过剩近似值,即<<,记a1=.若每次都取最简分数,继续使用“调日法”,将用“调日法”得到的的一列近似分数记为数列{an},则a5= .
题型5:数列的综合应用与创新问题
则第三次用“调日法”后,得;
a4=,
则第四次用“调日法”后,得;
解:
a5=.
初试身手
5.分形几何学又被称为“大自然的几何学”,是一门以不规则几何形态为研究对象的几何学.一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统,简单的说,分形就是研究无限复杂具备相似结构的几何学.下面用分形的方法得到一系列图形,如图1,正三角形的边长为1,在各边取两个三等分点,往外再作一个正三角形,得到图2中的图形;对图2中的各边做相同的操作,得到图3中的图形;以此类推,就得到了以下一系列图形,记第n个图形(图1为第一个图形)中的所有外围线段长的和为cn,则满足c1+c2+c3+…+cn>81的最小正整数n的值为________.(参考数据:lg 2≈0.301 0,lg 3≈0.477 1)
初试身手
解:
设第n个图形中线段的长度为an,则an=,
设第n个图形中线段的条数为bn,则bn=3×4n-1,
∴cn=anbn=3×,
则c1+c2+c3+…+cn=9×,
由题意知每个图形中每条线段的长度相等.
令9×>81,得>10,
则n>≈8.006,
即满足不等式的最小正整数n的值为9.
作业布置
作业: p54-56 复习参考题4 第3,5,6,7,11,12题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
