专项12:简易方程的实际问题“提升版”(解决问题)-2024-2025学年五年级数学上册期末核心考点(人教版)
文档属性
| 名称 | 专项12:简易方程的实际问题“提升版”(解决问题)-2024-2025学年五年级数学上册期末核心考点(人教版) | 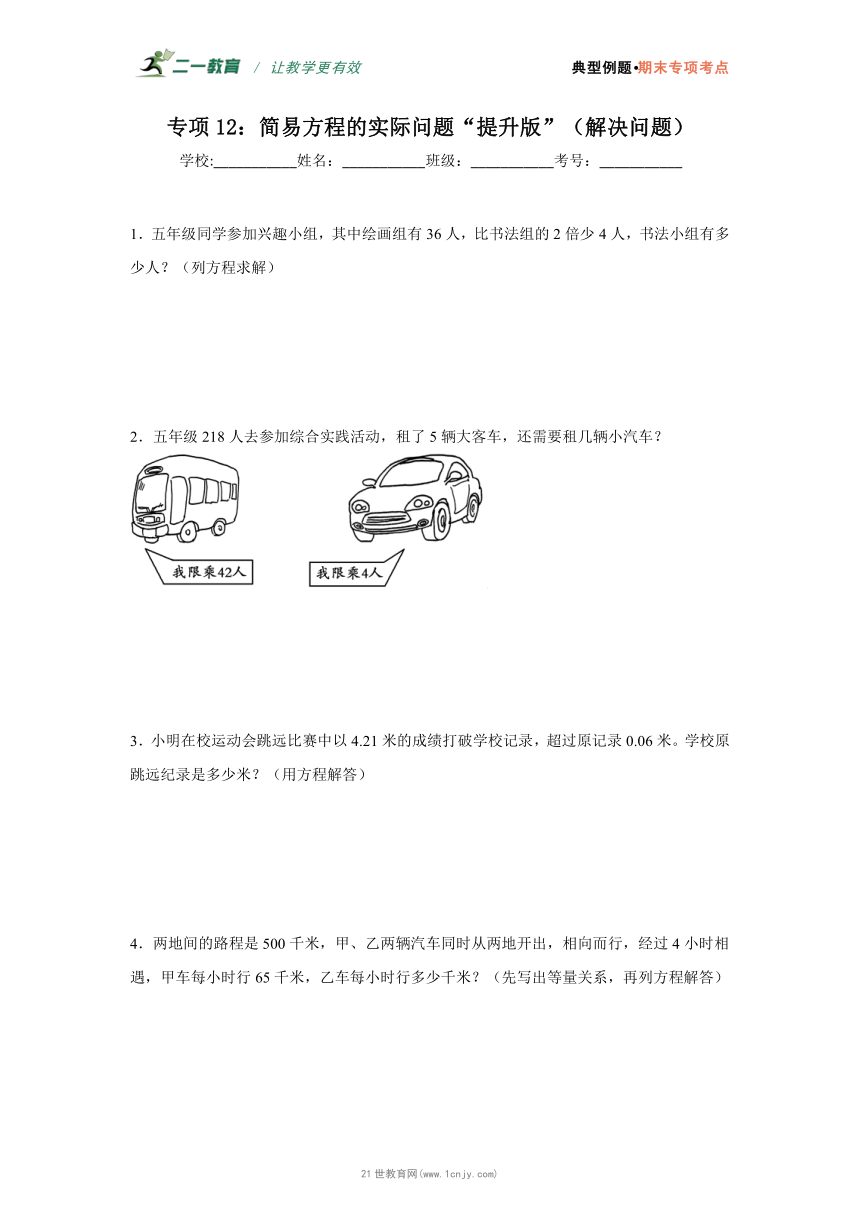 | |
| 格式 | doc | ||
| 文件大小 | 480.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-07 13:14:08 | ||
图片预览





文档简介
/ 让教学更有效 典型例题·期末专项考点
专项12:简易方程的实际问题“提升版”(解决问题)
学校:___________姓名:___________班级:___________考号:___________
1.五年级同学参加兴趣小组,其中绘画组有36人,比书法组的2倍少4人,书法小组有多少人?(列方程求解)
2.五年级218人去参加综合实践活动,租了5辆大客车,还需要租几辆小汽车?
3.小明在校运动会跳远比赛中以4.21米的成绩打破学校记录,超过原记录0.06米。学校原跳远纪录是多少米?(用方程解答)www-2-1-cnjy-com
4.两地间的路程是500千米,甲、乙两辆汽车同时从两地开出,相向而行,经过4小时相遇,甲车每小时行65千米,乙车每小时行多少千米?(先写出等量关系,再列方程解答)
5.实验小学合唱队女生有118人,比男生人数的1.2倍少2人。合唱队男生有多少人?(列方程解答)
6.山南中央公园占地约75公顷,其中水域面积大约是景观绿化面积的1.5倍。中央公园的水域面积和景观绿化面积大约各是多少公顷?(列方程解答)
7.小红的邮票枚数是小明的4倍,小红送给小明30枚邮票后和小明同样多。小红原来有多少枚邮票?
8.小永家和小刚家相距600米,他们同时从自己家出发,相向而行,经过6分钟相遇。小永每分钟走42米,小刚每分钟走多少米?
9.小刚和小强买同样的圆珠笔6支和4支,小刚比小强多付7元,每支圆珠笔多少元?
10.某品牌彩电的价钱是4700元/台,它比一种电冰箱3台价钱的3倍还多20元,每台电冰箱多少元?
11.两个工程队共同开凿一条长675米的隧道,两队分别从两端同时相向施工,25天打通。甲队每天开凿12米,乙队每天开凿多少米?【来源:21·世纪·教育·网】
12.小芳看一本300页的故事书,她每天看x页,已经看了7天,先用式子表示这本书还剩多少页没看?再计算当x=25时,还剩多少页没看?21*cnjy*com
13.朵朵和果果各跳了多少个?(列方程解答)
14.学校图书馆购买了本故事书和本文艺书,共花了260元,已知文艺书每本16元,那么,故事书每本多少元?21·世纪*教育网
15.鸡和兔子装在同一个笼子中,并且数量相同。两种动物的腿加起来共有48条。鸡有多少只?(用方程解答)
16.甲乙两人计划加工255个零件,两人同时开工,甲每时加工48个零件,乙每时加工37个零件,两人多长时间可以完成任务?(列方程解答)
17.“嫦娥五号”探测器实现了中国首次月球无人采样的任务并成功返回。它的质量高达8.2吨,比“嫦娥四号”的任务月球车的58倍还多0.08吨,“嫦娥四号”的任务月球车的质量约重多少吨?(用方程解答)2·1·c·n·j·y
18.一件夹克衫680元,比一条牛仔裤单价的3倍还多20元。买一条牛仔裤多少钱?
19.第七届世界军人运动会吉祥物名为“兵兵”,它的设计灵感来源于中国一级重点保护野生动物中华鲟。雌性中华鲟体长2.3米,比雄性中华鲟体长的2倍少1.1米。雄性中华鲟的体长是多少米?(用方程解)
20.一个芭比娃娃118元,比一个喜羊羊毛绒玩具的1.5倍少32元,喜羊羊毛绒玩具的价格是多少?
21.小区里有一个长方形花园,面积是600平方米,它的长是30米,宽是多少米?(用方程解)
22.妈妈的年龄比小丽年龄的4倍少3岁,妈妈今年37岁,小丽今年几岁?(列方程解决问题)
23.甲乙两城相距715千米。两列火车同时甲、乙两城相向开出,5.5小时后相遇。从甲车每小时行68千米,乙车每小时行多少千米?21cnjy.com
24.小明的爸爸买了24.8元的苹果,是买回橘子钱数的2倍。买橘子用了多少钱?(用方程解)
25.某手表厂计划每天生产手表30只,26天完成任务。实际提前6天就完成了任务。实际每天生产多少只手表?21教育网
26.甲、乙两个农场一共收获了80万吨小麦,甲农场收获的小麦比乙农场的4倍多10万吨,则甲、乙两个农场各收获了多少万吨小麦?
27.上海东方电视塔高468m,是亚洲第一高的电视塔。东方电视塔比北京中央电视塔高度的1.2倍多4.2m。中央电视塔高多少米?(用方程解答)
28.小店里有单价为15元/个和10元/个的悠悠球共20个,这些悠悠球的总价是245元,两种悠悠球各有多少个?
29.李爷爷家养羊284只,其中大羊的只数是小羊只数的3倍。大羊和小羊各有多少只?
30.鸭江寨村要修一条公路,先购进了两堆沙子,第一堆比第二堆多90吨。第一堆的质量是第二堆的2.5倍。两堆沙子各有多少吨?(用方程解)【来源:21cnj*y.co*m】
31.A、B两地相距120千米,甲车的速度为每小时55千米,乙车的速度为每小时45千米。
(1)两车分别从A、B两地同时同向而行(甲在乙后),经过多长时间甲车追上乙车?
(2)两车同时从A、B两地相向而行,经过多长时间两车相距10千米?
参考答案:
1.20人
【分析】根据题意可知,“书法组的人数×2-4=绘画组的人数”,据此列方程解答即可。
【详解】解:设书法组有x人;
2x-4=36
2x=40
x=20;
答:书法小组有20人。
【点睛】明确书法组和绘画组的人数关系是解答本题的关键。
2.2辆
【分析】根据题意可知,“大客车的辆数×可乘坐的人数+小汽车的辆数×可乘坐的人数=总人数”,据此列方程解答即可。
【详解】解:设还需要租x辆小汽车。
42×5+4x=218
210+4x=218
210+4x-210=218-210
4x=8
4x÷4=8÷4
x=2
答:还需要租2辆小汽车。
【点睛】找出题目中存在的等量关系式是解答本题的关键。
3.4.15米
【分析】假设学校原跳远纪录是x米,根据题目中的数量关系:原跳远纪录+0.06=小明在跳远比赛中的跳远成绩,代入数据列出方程,解方程即可求出学校原跳远纪录是多少米。
【详解】解:设学校原跳远纪录是x米,
x+0.06=4.21
x+0.06-0.06=4.21-0.06
x=4.15
答:学校原跳远纪录是4.15米。
【点睛】此题的解题关键是弄清题意,把学校原跳远纪录设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。21世纪教育网版权所有
4.(甲车行驶的速度+乙车行驶的速度)×相遇时间=甲、乙两地的路程;60千米
【分析】找出等量关系,即(甲车行驶的速度+乙车行驶的速度)×相遇时间=甲、乙两地的路程,据此设乙车每小时行x千米,列方程解答即可。
【详解】解:设乙车每小时行x千米。
答:乙车每小时行60千米。
【点睛】明确题中的等量关系是解题的关键。
5.100人
【分析】根据题意可知“男生人数×1.2-2=女生人数”,据此列方程解答即可。
【详解】解:设合唱队男生有x人;
1.2x-2=118
1.2x=120
x=100;
答:合唱队男生有100人。
【点睛】明确男、女生人数关系是解答本题的关键。
6.45公顷;30公顷
【分析】根据题意,假设景观绿化面积为x公顷,水域面积大约是景观绿化面积的1.5倍,所以水域面积为1.5x公顷,景观绿化面积+水域面积=中央公园面积,据此列出方程,求解即可。
【详解】解:设景观绿化面积为x公顷,水域面积为1.5x公顷,
x+1.5x=75
2.5x=75
x=75÷2.5
x=30
75-30=45(公顷)
答:中央公园的水域面积大约是45公顷,景观绿化面积大约是30公顷。
【点睛】此题的解题关键是弄清题意,把景观绿化面积设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。【出处:21教育名师】
7.80枚
【分析】根据题意可知“小明的邮票枚数×4=小红的邮票枚数”“小红的邮票枚数-30=小明的邮票枚数+30”据此列方程解答即可。
【详解】解:设小明的邮票枚数为x枚,则小红的邮票枚数为4x枚;
4x-30=x+30
3x=60
x=20;
20×4=80(枚);
答:小红原来有80枚邮票。
【点睛】明确小明和小红的邮票枚数关系是解答本题的关键。
8.58米
【分析】假设小刚每分钟走x米,根据速度和×相遇时间=路程,小永和小刚的速度和是(x+42)米/分,相遇时间是6分钟,路程是600米,代入到数量关系中,列出方程,解方程即可求出小刚每分钟走多少米。
【详解】解:设小刚每分钟走x米,
(x+42)×6=600
(x+42)×6÷6=600÷6
x+42=100
x+42-42=100-42
x=58
答:小刚每分钟走58米。
【点睛】此题的解题关键是弄清题意,把小刚每分钟走路的速度设为未知数x,利用题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。www.21-cn-jy.com
9.3.5元
【分析】设每支圆珠笔X元,根据等量关系“6支圆珠笔的价钱-4支圆珠笔的价钱=7元”列方程即可.
【详解】解:设每支圆珠笔x元
6x-4x=7
2x=7
x=3.5
答:每支圆珠笔3.5元。
【点睛】本题考查了列方程解应用题,关键是根据等量关系“6支圆珠笔的价钱-4支圆珠笔的价钱=7元列方程。
10.520元
【分析】根据题意,我们可以设每台电冰箱x元,再根据等量关系“电冰箱3台价钱的3倍+20元=一台彩电的价钱4700元”列出方程求解即可解答。
【详解】解:设每台电冰箱x元。
3x×3+20=4700
9x+20-20=4700-20
9x=4680
9x÷9=4680÷9
x=520
答:每台电冰箱520元。
11.15米
【分析】假设乙队每天开凿x米,根据题目中的数量关系:甲队每天开凿的长度×时间+乙队每天开凿的长度×时间=这条隧道的总长度,代入未知数和已知数据,列出方程,即可求解。
【详解】解:设乙队每天开凿x米。
12×25+x×25=675
300+25x=675
25x=675-300
25x=375
x=375÷25
x=15
答:乙队每天开凿15米。
【点睛】此题的解题关键是弄清题意,把乙队每天开凿的长度设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。
12.(300-7x)页;125页
【分析】先用小芳每天看的页数乘7表示出7天看了的页数,用这本书的页数减去看完的页数求出还没有看的页数;再求出当x=25时,还剩的未看的页数。
【详解】300-7×x=(300-7x)页
当x=25时,代入得300-7x=300-7×25=300-175=125(页)
答:这本书还剩(300-7x)页没看,当x=25时,还剩125页没看。
【点睛】解决此题关键是先用字母表示出看了的页数,进一步表示出还没看的页数,进而求出还没看的具体的页数。
13.朵朵83个;果果153个
【分析】根据“朵朵跳的个数+果果跳的个数=总个数”列方程解答即可。
【详解】解:设朵朵跳了x个,则果果跳了(2x-13)个;
x+2x-13=236
3x=249
x=83;
83×2-13
=166-13
=153(个)
答:朵朵跳了83个,果果跳了153个。
【点睛】列方程之前,一定要找出题目中存在的等量关系式。
14.元
【分析】先求出文艺书要花多少钱,用总共花的钱减去文艺书花的钱,就可以求出故事书花的钱,再除以故事书的数量,从而求出故事书每本多少钱。
【详解】购买文艺书用的钱数:元
购买故事书用的钱数:元
故事书的单价:(元)
答:故事书每本元。
【点睛】能够用式子表示出故事书总共花了多少钱是解题的关键。
15.8只
【分析】每只鸡有2条腿,每只兔子有4条腿,因为鸡和兔子的数量相同,且它们的腿加起来共有48条,可假设鸡、兔子各有x只,可列方程:4x+2x=48。
【详解】解:设鸡和兔子各有x只,
4x+2x=48
6x=48
x=48÷6
x=8
答:鸡有8只。
【点睛】本题属于鸡兔同笼问题,应用方程解答属于顺向思维。只要把相应的数字、字母代入数量关系式,就能列出方程。
16.3小时
【分析】设两人x小时可以完成任务,根据等量关系:甲每小时加工的零件个数×时间+乙每小时加工的零件个数×时间=零件的总个数,列方程解答即可。
【详解】解:设两人x小时可以完成任务,
48×x+37×x=255
(48+37)×x=255
85x=255
x=255÷85
x=3
答:两人3小时可以完成任务。
【点睛】本题考查了列方程解应用题,关键是根据等量关系列出方程。
17.0.14吨
【分析】假设“嫦娥四号”的任务月球车的质量是x吨,求一个数的几倍是多少,用乘法,所以题目中的数量关系为:“嫦娥四号”的任务月球车的质量×58+0.08=“嫦娥五号”探测器的质量,代入数据,据此列出方程,解方程即可求出“嫦娥四号”的任务月球车的质量。
【详解】解:设“嫦娥四号”的任务月球车的质量是x吨,
x×58+0.08=8.2
58x=8.2-0.08
58x=8.12
x=8.12÷58
x=0.14
答:“嫦娥四号”的任务月球车的质量约重0.14吨。
【点睛】此题的解题关键是弄清题意,把“嫦娥四号”的任务月球车的质量设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。
18.220元
【分析】假设一条牛仔裤单价是x元,根据数量关系:牛仔裤的单价×3+20=夹克衫的单价,已知一件夹克衫680元,代入数据和未知数,列出方程,解方程即可求出买一条牛仔裤多少钱。
【详解】解:设一条牛仔裤单价是x元。
x×3+20=680
3x=680-20
3x=660
x=660÷3
x=220
答:买一条牛仔裤220元。
【点睛】此题的解题关键是弄清题意,把牛仔裤的单价设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。
19.1.7米
【分析】可设雄性中华鲟的体长为x米,根据数量关系:雌性中华鲟体长=雄性中华鲟体长×2-1.1,据此列出方程,解答方程即可。
【详解】解:设雄性中华鲟的体长是x米。
答:雄性中华鲟的体长是1.7米。
20.100元
【分析】求一个数的几倍是多少,用乘法,可列数量关系:一个喜羊羊毛绒玩具的价格×1.5-32=一个芭比娃娃的价格,假设喜羊羊毛绒玩具的价格是x元,据此列出方程,解方程即可求出喜羊羊毛绒玩具的价格是多少。
【详解】解:设喜羊羊毛绒玩具的价格是x元,
1.5×x-32=118
1.5x-32+32=118+32
1.5x=150
1.5x÷1.5=150÷1.5
x=100
答:喜羊羊毛绒玩具的价格是100元。
【点睛】此题的解题关键是弄清题意,把喜羊羊毛绒玩具的价格设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。
21.20米
【分析】因为长方形的面积=长×宽,我们知道长和面积,那么就可设宽为未知数x,依此列方程并解答即可。
【详解】解:设长方形的宽为x米。
30x=600
x=600÷30
x=20
答:长方形的宽为20米。
【点睛】熟练掌握用方程解含一个未知数的问题是解答此题的关键。
22.10岁
【分析】根据题意可知,“小丽的年龄×4-3=妈妈的年龄”据此列方程解答即可。
【详解】解:设小丽今年x岁;
4x-3=37
4x=40
x=10;
答:小丽今年10岁。
【点睛】明确妈妈年龄和小丽年龄年龄之间的数量关系是解答本题的关键。
23.62千米
【分析】根据路程中相遇问题,速度和×相遇时间=相遇路程,设乙车每小时行x千米,根据(乙车的速度+甲车的速度)×相遇时间=相遇路程,据此列方程,解方程即可。
【详解】解:设乙车每小时行x千米。
(68+x)×5.5=715
374+5.5x=715
5.5x=341
x=62
答:乙车每小时行62千米。
【点睛】本题考查用方程解决问题,明确数量关系是解题的关键。
24.12.4元
【分析】由题意可知,设买橘子用了x元,根据等量关系:买橘子的钱数×2=24.8,据此列方程解答即可。2-1-c-n-j-y
【详解】解:设买橘子用了x元。
2x=24.8
2x÷2=24.8÷2
x=12.4
答:买橘子用了12.4元。
【点睛】本题考查用方程解决实际问题,明确等量关系是解题的关键。
25.39只
【分析】提前6天就完成了任务,实际用了(26-6)天。设实际每天生产x只手表,根据实际用的天数×实际每天生产数量=计划用的天数×计划每天生产数量,列出方程解答即可。
【详解】解:设实际每天生产x只手表。
(26-6)x=26×30
20x=780
20x÷20=780÷20
x=39
答:实际每天生产39只手表。
26.66万吨;14万吨
【分析】设乙农场收获了x万吨小麦,则甲农场收获了4x+10万吨小麦,根据甲农场收获小麦吨数+乙农场收获小麦吨数=80万吨,列出方程求出x的值是乙农场收获小麦吨数,两个农场共收获小麦吨数-乙农场收获小麦吨数=甲农场收获小麦吨数,据此列式解答。
【详解】解:设乙农场收获了x万吨小麦。
4x+10+x=80
5x+10-10=80-10
5x÷5=70÷5
x=14
80-14=66(万吨)
答:甲、乙两个农场各收获了66万吨、14万吨小麦。
【点睛】用方程解决问题的关键是找到等量关系。
27.386.5米
【分析】可假设中央电视塔高x米,则东方电视塔高1.2x+4.2(米),而同时又已知东方电视塔高468米,则可列方程:1.2x+4.2=468。21教育名师原创作品
【详解】解:设中央电视塔高x米,由题意得,
1.2x+4.2=468
1.2x=468-4.2
1.2x=463.8
x=386.5
答:中央电视塔高386.5米。
【点睛】一般都是先找出1倍量,并结合题意将它设为未知数,最后依据题目里的数量关系列出恰当的方程。
28.15元/个的9个;10元/个的11个
【分析】把15元/个悠悠球的个数设为未知数,10元/个悠悠球的个数=悠悠球的总个数-15元/个悠悠球的个数,等量关系式:15元/个悠悠球的个数×15+10元/个悠悠球的个数×10=悠悠球的总价,据此列方程解答。21*cnjy*com
【详解】解:设15元/个的悠悠球有x个,则10元/个的悠悠球有(20-x)个。
15x+(20-x)×10=245
15x+20×10-10x=245
15x+200-10x=245
15x-10x+200=245
5x+200=245
5x+200-200=245-200
5x=45
5x÷5=45÷5
x=9
20-9=11(个)
答:15元/个的悠悠球有9个,10元/个的悠悠球有11个。
【点睛】准确设出未知数并找出题目中的等量关系是解答题目的关键。
29.大羊213只,小羊71只
【分析】将小羊的数量设为未知数x只,那么大羊有3x只。据此,根据“大羊+小羊=284只”这一等量关系,列方程解方程即可。21·cn·jy·com
【详解】解:设小羊有x只。
x+3x=284
4x=284
x=284÷4
x=71
71×3=213(只)
答:大羊有213只,小羊有71只。
【点睛】本题考查了简易方程的应用,解题关键在于找出等量关系并列方程。
30.第一堆150吨;第二堆60吨
【分析】把第二堆沙子的质量设为未知数,第一堆沙子的质量=第二堆沙子的质量×2.5,等量关系式:第一堆沙子的质量-第二堆沙子的质量=90吨,据此列方程解答。
【详解】解:设第二堆沙子有x吨,则第一堆沙子有2.5x吨。
2.5x-x=90
1.5x=90
x=90÷1.5
x=60
2.5×60=150(吨)
答:第一堆沙子有150吨,第二堆沙子有60吨。
【点睛】本题主要考查列方程解决实际问题,明确题目中存在的等量关系是解答本题的关键。
31.(1)12小时;(2)1.1小时或1.3小时
【分析】因为A、B两地相距120千米,得到总路程为120千米,甲车的速度为每小时55千米,乙车的速度为每小时45千米。(1)这是追及问题,我们可以设经过x小时甲车追上乙车,用甲车的速度减去乙车的速度得到甲乙两车的速度差,再用路程差除以两车速度差,即可得。(2)这是相遇问题的,要分两种情况进行讨论,未相遇时相距10千米和相遇后相距10千米,即可用需要行的路程(120-10)千米或(120+10)千米,分别除以两车速度和,即可得。【版权所有:21教育】
【详解】(1)解:设经过x小时甲车追上乙车。
(55-45)x=120
10x=120
x=120÷10
x=12
答:经过12小时甲车追上乙车。
(2)解:设经过y小时两车相距10千米。
两车未相遇时:(55+45)y=120-10
100y=110
y=110÷100
y=1.1
两车相遇后:(55+45)y=120+10
100y=130
y=130÷100
y=1.3
答:经过1.1小时或1.3小时两车相距10千米。
【点睛】此题考查的是行程问题,分清相遇问题与追及问题是解题的关键。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
专项12:简易方程的实际问题“提升版”(解决问题)
学校:___________姓名:___________班级:___________考号:___________
1.五年级同学参加兴趣小组,其中绘画组有36人,比书法组的2倍少4人,书法小组有多少人?(列方程求解)
2.五年级218人去参加综合实践活动,租了5辆大客车,还需要租几辆小汽车?
3.小明在校运动会跳远比赛中以4.21米的成绩打破学校记录,超过原记录0.06米。学校原跳远纪录是多少米?(用方程解答)www-2-1-cnjy-com
4.两地间的路程是500千米,甲、乙两辆汽车同时从两地开出,相向而行,经过4小时相遇,甲车每小时行65千米,乙车每小时行多少千米?(先写出等量关系,再列方程解答)
5.实验小学合唱队女生有118人,比男生人数的1.2倍少2人。合唱队男生有多少人?(列方程解答)
6.山南中央公园占地约75公顷,其中水域面积大约是景观绿化面积的1.5倍。中央公园的水域面积和景观绿化面积大约各是多少公顷?(列方程解答)
7.小红的邮票枚数是小明的4倍,小红送给小明30枚邮票后和小明同样多。小红原来有多少枚邮票?
8.小永家和小刚家相距600米,他们同时从自己家出发,相向而行,经过6分钟相遇。小永每分钟走42米,小刚每分钟走多少米?
9.小刚和小强买同样的圆珠笔6支和4支,小刚比小强多付7元,每支圆珠笔多少元?
10.某品牌彩电的价钱是4700元/台,它比一种电冰箱3台价钱的3倍还多20元,每台电冰箱多少元?
11.两个工程队共同开凿一条长675米的隧道,两队分别从两端同时相向施工,25天打通。甲队每天开凿12米,乙队每天开凿多少米?【来源:21·世纪·教育·网】
12.小芳看一本300页的故事书,她每天看x页,已经看了7天,先用式子表示这本书还剩多少页没看?再计算当x=25时,还剩多少页没看?21*cnjy*com
13.朵朵和果果各跳了多少个?(列方程解答)
14.学校图书馆购买了本故事书和本文艺书,共花了260元,已知文艺书每本16元,那么,故事书每本多少元?21·世纪*教育网
15.鸡和兔子装在同一个笼子中,并且数量相同。两种动物的腿加起来共有48条。鸡有多少只?(用方程解答)
16.甲乙两人计划加工255个零件,两人同时开工,甲每时加工48个零件,乙每时加工37个零件,两人多长时间可以完成任务?(列方程解答)
17.“嫦娥五号”探测器实现了中国首次月球无人采样的任务并成功返回。它的质量高达8.2吨,比“嫦娥四号”的任务月球车的58倍还多0.08吨,“嫦娥四号”的任务月球车的质量约重多少吨?(用方程解答)2·1·c·n·j·y
18.一件夹克衫680元,比一条牛仔裤单价的3倍还多20元。买一条牛仔裤多少钱?
19.第七届世界军人运动会吉祥物名为“兵兵”,它的设计灵感来源于中国一级重点保护野生动物中华鲟。雌性中华鲟体长2.3米,比雄性中华鲟体长的2倍少1.1米。雄性中华鲟的体长是多少米?(用方程解)
20.一个芭比娃娃118元,比一个喜羊羊毛绒玩具的1.5倍少32元,喜羊羊毛绒玩具的价格是多少?
21.小区里有一个长方形花园,面积是600平方米,它的长是30米,宽是多少米?(用方程解)
22.妈妈的年龄比小丽年龄的4倍少3岁,妈妈今年37岁,小丽今年几岁?(列方程解决问题)
23.甲乙两城相距715千米。两列火车同时甲、乙两城相向开出,5.5小时后相遇。从甲车每小时行68千米,乙车每小时行多少千米?21cnjy.com
24.小明的爸爸买了24.8元的苹果,是买回橘子钱数的2倍。买橘子用了多少钱?(用方程解)
25.某手表厂计划每天生产手表30只,26天完成任务。实际提前6天就完成了任务。实际每天生产多少只手表?21教育网
26.甲、乙两个农场一共收获了80万吨小麦,甲农场收获的小麦比乙农场的4倍多10万吨,则甲、乙两个农场各收获了多少万吨小麦?
27.上海东方电视塔高468m,是亚洲第一高的电视塔。东方电视塔比北京中央电视塔高度的1.2倍多4.2m。中央电视塔高多少米?(用方程解答)
28.小店里有单价为15元/个和10元/个的悠悠球共20个,这些悠悠球的总价是245元,两种悠悠球各有多少个?
29.李爷爷家养羊284只,其中大羊的只数是小羊只数的3倍。大羊和小羊各有多少只?
30.鸭江寨村要修一条公路,先购进了两堆沙子,第一堆比第二堆多90吨。第一堆的质量是第二堆的2.5倍。两堆沙子各有多少吨?(用方程解)【来源:21cnj*y.co*m】
31.A、B两地相距120千米,甲车的速度为每小时55千米,乙车的速度为每小时45千米。
(1)两车分别从A、B两地同时同向而行(甲在乙后),经过多长时间甲车追上乙车?
(2)两车同时从A、B两地相向而行,经过多长时间两车相距10千米?
参考答案:
1.20人
【分析】根据题意可知,“书法组的人数×2-4=绘画组的人数”,据此列方程解答即可。
【详解】解:设书法组有x人;
2x-4=36
2x=40
x=20;
答:书法小组有20人。
【点睛】明确书法组和绘画组的人数关系是解答本题的关键。
2.2辆
【分析】根据题意可知,“大客车的辆数×可乘坐的人数+小汽车的辆数×可乘坐的人数=总人数”,据此列方程解答即可。
【详解】解:设还需要租x辆小汽车。
42×5+4x=218
210+4x=218
210+4x-210=218-210
4x=8
4x÷4=8÷4
x=2
答:还需要租2辆小汽车。
【点睛】找出题目中存在的等量关系式是解答本题的关键。
3.4.15米
【分析】假设学校原跳远纪录是x米,根据题目中的数量关系:原跳远纪录+0.06=小明在跳远比赛中的跳远成绩,代入数据列出方程,解方程即可求出学校原跳远纪录是多少米。
【详解】解:设学校原跳远纪录是x米,
x+0.06=4.21
x+0.06-0.06=4.21-0.06
x=4.15
答:学校原跳远纪录是4.15米。
【点睛】此题的解题关键是弄清题意,把学校原跳远纪录设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。21世纪教育网版权所有
4.(甲车行驶的速度+乙车行驶的速度)×相遇时间=甲、乙两地的路程;60千米
【分析】找出等量关系,即(甲车行驶的速度+乙车行驶的速度)×相遇时间=甲、乙两地的路程,据此设乙车每小时行x千米,列方程解答即可。
【详解】解:设乙车每小时行x千米。
答:乙车每小时行60千米。
【点睛】明确题中的等量关系是解题的关键。
5.100人
【分析】根据题意可知“男生人数×1.2-2=女生人数”,据此列方程解答即可。
【详解】解:设合唱队男生有x人;
1.2x-2=118
1.2x=120
x=100;
答:合唱队男生有100人。
【点睛】明确男、女生人数关系是解答本题的关键。
6.45公顷;30公顷
【分析】根据题意,假设景观绿化面积为x公顷,水域面积大约是景观绿化面积的1.5倍,所以水域面积为1.5x公顷,景观绿化面积+水域面积=中央公园面积,据此列出方程,求解即可。
【详解】解:设景观绿化面积为x公顷,水域面积为1.5x公顷,
x+1.5x=75
2.5x=75
x=75÷2.5
x=30
75-30=45(公顷)
答:中央公园的水域面积大约是45公顷,景观绿化面积大约是30公顷。
【点睛】此题的解题关键是弄清题意,把景观绿化面积设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。【出处:21教育名师】
7.80枚
【分析】根据题意可知“小明的邮票枚数×4=小红的邮票枚数”“小红的邮票枚数-30=小明的邮票枚数+30”据此列方程解答即可。
【详解】解:设小明的邮票枚数为x枚,则小红的邮票枚数为4x枚;
4x-30=x+30
3x=60
x=20;
20×4=80(枚);
答:小红原来有80枚邮票。
【点睛】明确小明和小红的邮票枚数关系是解答本题的关键。
8.58米
【分析】假设小刚每分钟走x米,根据速度和×相遇时间=路程,小永和小刚的速度和是(x+42)米/分,相遇时间是6分钟,路程是600米,代入到数量关系中,列出方程,解方程即可求出小刚每分钟走多少米。
【详解】解:设小刚每分钟走x米,
(x+42)×6=600
(x+42)×6÷6=600÷6
x+42=100
x+42-42=100-42
x=58
答:小刚每分钟走58米。
【点睛】此题的解题关键是弄清题意,把小刚每分钟走路的速度设为未知数x,利用题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。www.21-cn-jy.com
9.3.5元
【分析】设每支圆珠笔X元,根据等量关系“6支圆珠笔的价钱-4支圆珠笔的价钱=7元”列方程即可.
【详解】解:设每支圆珠笔x元
6x-4x=7
2x=7
x=3.5
答:每支圆珠笔3.5元。
【点睛】本题考查了列方程解应用题,关键是根据等量关系“6支圆珠笔的价钱-4支圆珠笔的价钱=7元列方程。
10.520元
【分析】根据题意,我们可以设每台电冰箱x元,再根据等量关系“电冰箱3台价钱的3倍+20元=一台彩电的价钱4700元”列出方程求解即可解答。
【详解】解:设每台电冰箱x元。
3x×3+20=4700
9x+20-20=4700-20
9x=4680
9x÷9=4680÷9
x=520
答:每台电冰箱520元。
11.15米
【分析】假设乙队每天开凿x米,根据题目中的数量关系:甲队每天开凿的长度×时间+乙队每天开凿的长度×时间=这条隧道的总长度,代入未知数和已知数据,列出方程,即可求解。
【详解】解:设乙队每天开凿x米。
12×25+x×25=675
300+25x=675
25x=675-300
25x=375
x=375÷25
x=15
答:乙队每天开凿15米。
【点睛】此题的解题关键是弄清题意,把乙队每天开凿的长度设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。
12.(300-7x)页;125页
【分析】先用小芳每天看的页数乘7表示出7天看了的页数,用这本书的页数减去看完的页数求出还没有看的页数;再求出当x=25时,还剩的未看的页数。
【详解】300-7×x=(300-7x)页
当x=25时,代入得300-7x=300-7×25=300-175=125(页)
答:这本书还剩(300-7x)页没看,当x=25时,还剩125页没看。
【点睛】解决此题关键是先用字母表示出看了的页数,进一步表示出还没看的页数,进而求出还没看的具体的页数。
13.朵朵83个;果果153个
【分析】根据“朵朵跳的个数+果果跳的个数=总个数”列方程解答即可。
【详解】解:设朵朵跳了x个,则果果跳了(2x-13)个;
x+2x-13=236
3x=249
x=83;
83×2-13
=166-13
=153(个)
答:朵朵跳了83个,果果跳了153个。
【点睛】列方程之前,一定要找出题目中存在的等量关系式。
14.元
【分析】先求出文艺书要花多少钱,用总共花的钱减去文艺书花的钱,就可以求出故事书花的钱,再除以故事书的数量,从而求出故事书每本多少钱。
【详解】购买文艺书用的钱数:元
购买故事书用的钱数:元
故事书的单价:(元)
答:故事书每本元。
【点睛】能够用式子表示出故事书总共花了多少钱是解题的关键。
15.8只
【分析】每只鸡有2条腿,每只兔子有4条腿,因为鸡和兔子的数量相同,且它们的腿加起来共有48条,可假设鸡、兔子各有x只,可列方程:4x+2x=48。
【详解】解:设鸡和兔子各有x只,
4x+2x=48
6x=48
x=48÷6
x=8
答:鸡有8只。
【点睛】本题属于鸡兔同笼问题,应用方程解答属于顺向思维。只要把相应的数字、字母代入数量关系式,就能列出方程。
16.3小时
【分析】设两人x小时可以完成任务,根据等量关系:甲每小时加工的零件个数×时间+乙每小时加工的零件个数×时间=零件的总个数,列方程解答即可。
【详解】解:设两人x小时可以完成任务,
48×x+37×x=255
(48+37)×x=255
85x=255
x=255÷85
x=3
答:两人3小时可以完成任务。
【点睛】本题考查了列方程解应用题,关键是根据等量关系列出方程。
17.0.14吨
【分析】假设“嫦娥四号”的任务月球车的质量是x吨,求一个数的几倍是多少,用乘法,所以题目中的数量关系为:“嫦娥四号”的任务月球车的质量×58+0.08=“嫦娥五号”探测器的质量,代入数据,据此列出方程,解方程即可求出“嫦娥四号”的任务月球车的质量。
【详解】解:设“嫦娥四号”的任务月球车的质量是x吨,
x×58+0.08=8.2
58x=8.2-0.08
58x=8.12
x=8.12÷58
x=0.14
答:“嫦娥四号”的任务月球车的质量约重0.14吨。
【点睛】此题的解题关键是弄清题意,把“嫦娥四号”的任务月球车的质量设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。
18.220元
【分析】假设一条牛仔裤单价是x元,根据数量关系:牛仔裤的单价×3+20=夹克衫的单价,已知一件夹克衫680元,代入数据和未知数,列出方程,解方程即可求出买一条牛仔裤多少钱。
【详解】解:设一条牛仔裤单价是x元。
x×3+20=680
3x=680-20
3x=660
x=660÷3
x=220
答:买一条牛仔裤220元。
【点睛】此题的解题关键是弄清题意,把牛仔裤的单价设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。
19.1.7米
【分析】可设雄性中华鲟的体长为x米,根据数量关系:雌性中华鲟体长=雄性中华鲟体长×2-1.1,据此列出方程,解答方程即可。
【详解】解:设雄性中华鲟的体长是x米。
答:雄性中华鲟的体长是1.7米。
20.100元
【分析】求一个数的几倍是多少,用乘法,可列数量关系:一个喜羊羊毛绒玩具的价格×1.5-32=一个芭比娃娃的价格,假设喜羊羊毛绒玩具的价格是x元,据此列出方程,解方程即可求出喜羊羊毛绒玩具的价格是多少。
【详解】解:设喜羊羊毛绒玩具的价格是x元,
1.5×x-32=118
1.5x-32+32=118+32
1.5x=150
1.5x÷1.5=150÷1.5
x=100
答:喜羊羊毛绒玩具的价格是100元。
【点睛】此题的解题关键是弄清题意,把喜羊羊毛绒玩具的价格设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。
21.20米
【分析】因为长方形的面积=长×宽,我们知道长和面积,那么就可设宽为未知数x,依此列方程并解答即可。
【详解】解:设长方形的宽为x米。
30x=600
x=600÷30
x=20
答:长方形的宽为20米。
【点睛】熟练掌握用方程解含一个未知数的问题是解答此题的关键。
22.10岁
【分析】根据题意可知,“小丽的年龄×4-3=妈妈的年龄”据此列方程解答即可。
【详解】解:设小丽今年x岁;
4x-3=37
4x=40
x=10;
答:小丽今年10岁。
【点睛】明确妈妈年龄和小丽年龄年龄之间的数量关系是解答本题的关键。
23.62千米
【分析】根据路程中相遇问题,速度和×相遇时间=相遇路程,设乙车每小时行x千米,根据(乙车的速度+甲车的速度)×相遇时间=相遇路程,据此列方程,解方程即可。
【详解】解:设乙车每小时行x千米。
(68+x)×5.5=715
374+5.5x=715
5.5x=341
x=62
答:乙车每小时行62千米。
【点睛】本题考查用方程解决问题,明确数量关系是解题的关键。
24.12.4元
【分析】由题意可知,设买橘子用了x元,根据等量关系:买橘子的钱数×2=24.8,据此列方程解答即可。2-1-c-n-j-y
【详解】解:设买橘子用了x元。
2x=24.8
2x÷2=24.8÷2
x=12.4
答:买橘子用了12.4元。
【点睛】本题考查用方程解决实际问题,明确等量关系是解题的关键。
25.39只
【分析】提前6天就完成了任务,实际用了(26-6)天。设实际每天生产x只手表,根据实际用的天数×实际每天生产数量=计划用的天数×计划每天生产数量,列出方程解答即可。
【详解】解:设实际每天生产x只手表。
(26-6)x=26×30
20x=780
20x÷20=780÷20
x=39
答:实际每天生产39只手表。
26.66万吨;14万吨
【分析】设乙农场收获了x万吨小麦,则甲农场收获了4x+10万吨小麦,根据甲农场收获小麦吨数+乙农场收获小麦吨数=80万吨,列出方程求出x的值是乙农场收获小麦吨数,两个农场共收获小麦吨数-乙农场收获小麦吨数=甲农场收获小麦吨数,据此列式解答。
【详解】解:设乙农场收获了x万吨小麦。
4x+10+x=80
5x+10-10=80-10
5x÷5=70÷5
x=14
80-14=66(万吨)
答:甲、乙两个农场各收获了66万吨、14万吨小麦。
【点睛】用方程解决问题的关键是找到等量关系。
27.386.5米
【分析】可假设中央电视塔高x米,则东方电视塔高1.2x+4.2(米),而同时又已知东方电视塔高468米,则可列方程:1.2x+4.2=468。21教育名师原创作品
【详解】解:设中央电视塔高x米,由题意得,
1.2x+4.2=468
1.2x=468-4.2
1.2x=463.8
x=386.5
答:中央电视塔高386.5米。
【点睛】一般都是先找出1倍量,并结合题意将它设为未知数,最后依据题目里的数量关系列出恰当的方程。
28.15元/个的9个;10元/个的11个
【分析】把15元/个悠悠球的个数设为未知数,10元/个悠悠球的个数=悠悠球的总个数-15元/个悠悠球的个数,等量关系式:15元/个悠悠球的个数×15+10元/个悠悠球的个数×10=悠悠球的总价,据此列方程解答。21*cnjy*com
【详解】解:设15元/个的悠悠球有x个,则10元/个的悠悠球有(20-x)个。
15x+(20-x)×10=245
15x+20×10-10x=245
15x+200-10x=245
15x-10x+200=245
5x+200=245
5x+200-200=245-200
5x=45
5x÷5=45÷5
x=9
20-9=11(个)
答:15元/个的悠悠球有9个,10元/个的悠悠球有11个。
【点睛】准确设出未知数并找出题目中的等量关系是解答题目的关键。
29.大羊213只,小羊71只
【分析】将小羊的数量设为未知数x只,那么大羊有3x只。据此,根据“大羊+小羊=284只”这一等量关系,列方程解方程即可。21·cn·jy·com
【详解】解:设小羊有x只。
x+3x=284
4x=284
x=284÷4
x=71
71×3=213(只)
答:大羊有213只,小羊有71只。
【点睛】本题考查了简易方程的应用,解题关键在于找出等量关系并列方程。
30.第一堆150吨;第二堆60吨
【分析】把第二堆沙子的质量设为未知数,第一堆沙子的质量=第二堆沙子的质量×2.5,等量关系式:第一堆沙子的质量-第二堆沙子的质量=90吨,据此列方程解答。
【详解】解:设第二堆沙子有x吨,则第一堆沙子有2.5x吨。
2.5x-x=90
1.5x=90
x=90÷1.5
x=60
2.5×60=150(吨)
答:第一堆沙子有150吨,第二堆沙子有60吨。
【点睛】本题主要考查列方程解决实际问题,明确题目中存在的等量关系是解答本题的关键。
31.(1)12小时;(2)1.1小时或1.3小时
【分析】因为A、B两地相距120千米,得到总路程为120千米,甲车的速度为每小时55千米,乙车的速度为每小时45千米。(1)这是追及问题,我们可以设经过x小时甲车追上乙车,用甲车的速度减去乙车的速度得到甲乙两车的速度差,再用路程差除以两车速度差,即可得。(2)这是相遇问题的,要分两种情况进行讨论,未相遇时相距10千米和相遇后相距10千米,即可用需要行的路程(120-10)千米或(120+10)千米,分别除以两车速度和,即可得。【版权所有:21教育】
【详解】(1)解:设经过x小时甲车追上乙车。
(55-45)x=120
10x=120
x=120÷10
x=12
答:经过12小时甲车追上乙车。
(2)解:设经过y小时两车相距10千米。
两车未相遇时:(55+45)y=120-10
100y=110
y=110÷100
y=1.1
两车相遇后:(55+45)y=120+10
100y=130
y=130÷100
y=1.3
答:经过1.1小时或1.3小时两车相距10千米。
【点睛】此题考查的是行程问题,分清相遇问题与追及问题是解题的关键。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
同课章节目录
