湖北省恩施市小渡船初中2024-2025学年上学期八年级12月数学试题卷(含答案)
文档属性
| 名称 | 湖北省恩施市小渡船初中2024-2025学年上学期八年级12月数学试题卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 337.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 20:53:10 | ||
图片预览




文档简介
2024-2025学年八年级数学上学期12月考卷
第一部分(选择题 共30分)
一、选择题(本大题共10小题,每小题3分,满分30分.在每个小题给出的四个选项中,只有一项符合题目要求的)
1.下面四个手机应用图标中是轴对称图形的是( )
A. B. C. D.
2.下列各项计算结果是a8的是( )
A.a4 a2 B.a2+a4 C.(a3)5 D.a10÷a2
3.如图,将△ABC沿着平行于BC的直线DE折叠,点A落在点A'处,若∠B=44°,则∠A'DB的度数是( )
A.44° B.92° C.108° D.88°
4.下列运算正确的是( )
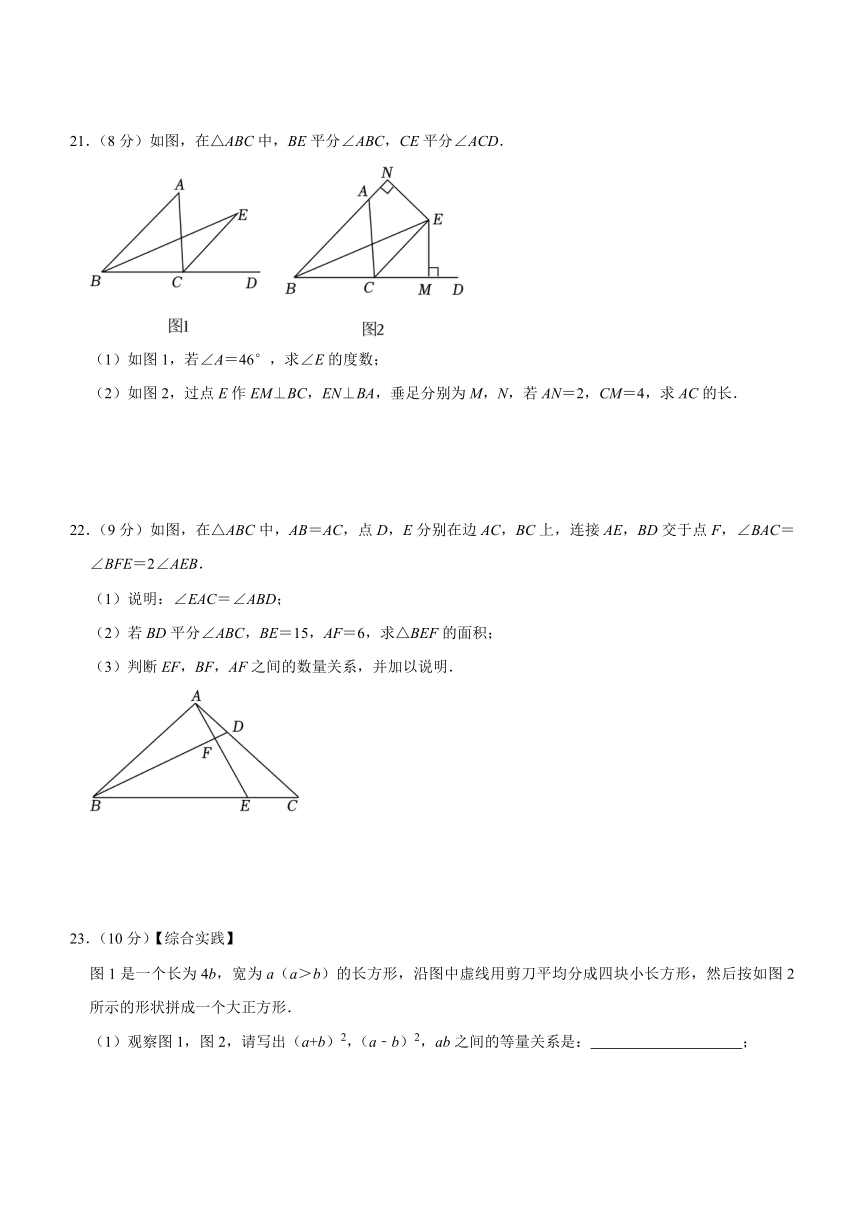
A.(﹣2a)2=﹣4a2 B.(a﹣b)2=a2﹣b2
C.(﹣m+2)(﹣m﹣2)=m2﹣4 D.(a5)2=a7
5.如图,△ABC中,BD平分∠ABC,EF垂直平分BC交BC于点E,交BD于点F,连接CF,若∠A=60°,∠ABD=25°,则∠ACF的度数为( )
A.25° B.45° C.50° D.70°
6.若(x2﹣px+q)(x﹣3)展开后不含x的一次项,则p与q的关系是( )
A.p=3q B.p+3q=0 C.q+3p=0 D.q=3p
7.如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CD于点D,BE⊥CD于点E.若BE=7,CE=3,则△ADE的面积是( )
A.6 B.21 C.12 D.24
8.已知2m﹣n=3,4m2﹣3mn+n2=14,则mn的值为( )
A.3 B.4 C.5 D.6
9.如图,在△ABC中,∠BAC=80°,边AB的垂直平分线交AB于点D,交BC于点E,边AC的垂直平分线交AC于点F,交BC于点G,连接AE,AG.则∠EAG的度数为( )
A.35° B.30° C.25° D.20°
10.如图,在△ABC中,AB=AC,BD为AC边上的高,BE平分∠ABD,点F在BD上,连接EF并延长交BC于点G,若BG=EG,∠A=2∠DEF,有下列结论:①∠DEF=∠CBD;②∠ABE+∠CBD=45°; ③EG⊥BC; ④BF=CE.其中正确的结论有( )
A.1个 B.4个 C.3个 D.2个
第二部分(选择题 共90分)
二、填空题(本大题共5小题,每小题3分,满分15分)
11.已知点A(a+3,5)与点B(5,b)关于y轴对称,则b﹣a的值是 .
12.如果x2+2(m﹣1)x+4是一个完全平方式,则m= .
13.一个正方形、一个正三角形和一个正五边形如图摆放,若∠3=34°,则∠1+∠2= °.
14.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=12cm,动点P从点A出发,沿AB向点B运动,动点Q从点B出发,沿BC向点C运动,如果动点P以2cm/s,Q以1cm/s的速度同时出发.设运动时间为t(s),P、Q在运动过程中,△PBQ的形状不断发生变化,当t 时,△PBQ是直角三角形.
15.如图,在Rt△ABC中,∠ACB=90°,BD平分∠ABC,E是AB上一点,且AE=AD,连接DE,过E作EF⊥BD,垂足为F,延长EF交BC于点G.现给出以下结论:①EF=FG;②CD=DE;③∠BEG=∠BDC;④∠DEF=45°.其中正确的是 .(写出所有正确结论的序号)
三、解答题(本大题共9小题,满分75分.解答应写出文字说明,证明过程或演算步骤)
16.(每小题3分,共6分)计算:
(1)a2 a4+(﹣2a2)3+a8÷a2; (2)y(3﹣4y)﹣(x+2y)(x﹣2y).
17.(每小题3分,共6分)因式分解:
(1) (a+1)2+2a(a+1). (2)25(m+n)2﹣9(m﹣n)2.
18.(6分)如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)若∠B=30°,∠BAC=130°,求∠E的度数;
(2)求证:∠BAC=∠B+2∠E.
19.(每小题5分,共10分)化简求值:
(1)2(x﹣5)(x+2)﹣(x﹣1)(2x+1),其中x=﹣2;
(2)[(a+3b)(﹣a+3b)﹣(2a﹣3b)2﹣5a(a﹣4b)]÷(2a),其中a=2,b.
20.(8分)如图所示,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,2),
C(2,3).
(1)在图中画出△ABC关于x轴对称的图形△A1B1C1;
(2)在图中,若B2(﹣4,2)与点B关于一条直线成轴对称,此时C点关于直线的对称点C2的坐标为 ;
(3)△A1B1C1的面积为 .
21.(8分)如图,在△ABC中,BE平分∠ABC,CE平分∠ACD.
(1)如图1,若∠A=46°,求∠E的度数;
(2)如图2,过点E作EM⊥BC,EN⊥BA,垂足分别为M,N,若AN=2,CM=4,求AC的长.
22.(9分)如图,在△ABC中,AB=AC,点D,E分别在边AC,BC上,连接AE,BD交于点F,∠BAC=∠BFE=2∠AEB.
(1)说明:∠EAC=∠ABD;
(2)若BD平分∠ABC,BE=15,AF=6,求△BEF的面积;
(3)判断EF,BF,AF之间的数量关系,并加以说明.
23.(10分)【综合实践】
图1是一个长为4b,宽为a(a>b)的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按如图2所示的形状拼成一个大正方形.
(1)观察图1,图2,请写出(a+b)2,(a﹣b)2,ab之间的等量关系是: ;
(2)已知(m+n)2=25,(m﹣n)2=16,求m2+n2的值;
(3)如图3,C是线段AB上的一点,以AC,BC为边向上分别作正方形ACDE和正方形BCFG,连接AF.若AB=7,DF=3,求△AFC的面积.
24.(12分)(1)如图1,∠BAD=90°,AB=AD,过点B作BC⊥AC于点C,过点D作DE⊥AC于点E.
求证:△ABC≌△DAE.
(2)如图2,等腰Rt△ABC中,∠BAC=90°,AB=AC,点A是y轴正半轴上的一动点,点B在x轴的正半轴上.以OA为直角边在y轴的左边作等腰Rt△OAD,AO=AD,连接CD,试问A点在运动过程中△AOB与△ACD面积的比值是否会发生变化?如果没有变化,请求出;若变化,请说明理由.
(3)如图3,在平面直角坐标系xOy中,点P的坐标为(2,6),点Q为第二象限内任一点.若△POQ是以OP为边的等腰直角三角形,请直接写出点Q的坐标.
参考答案
选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1 2 3 4 5 6 7 8 9 10
D D B C B C A C D B
二、填空题(本大题共5小题,每小题3分,共15分)
11.13 12.3或﹣1 13.
14.或6 15.①③④
三、解答题(本大题共9小题,满分75分.解答应写出文字说明,证明过程或演算步骤)
16.(每小题3分,共6分)
【解答】解:(1)a2 a4+(﹣2a2)3+a8÷a2
=a6﹣8a6+a6
=﹣6a6; …………………………(3分)
(2)y(3﹣4y)﹣(x+2y)(x﹣2y)
=3y﹣4y2﹣(x2﹣4y2)
=3y﹣4y2﹣x2+4y2
=3y﹣x2. …………………………(3分)
17.(每小题3分,共6分)
【解答】解:
(1)原式=(a+1)[(a+1)+2a]
=(a+1)(3a+1). …………………………(3分)
(2)原式=[5(m+n)]2﹣[3(m﹣n)]2
=(5m+5n)2﹣(3m﹣3n)2
=[(5m+5n)﹣(3m﹣3n)][(5m+5n)+(3m﹣3n)]
=(2m+8n)(8m+2n)
=4(m+4n)(4m+n); …………………………(3分)
18.(6分)
【解答】(1)解:∵∠B=30°,∠BAC=130°,
∴∠ACD=∠B+∠BAC=160°,
∵CE平分∠ACD,
∴∠ECD∠ACD=80°,
∴∠E=∠ECD﹣∠B=50°; …………………………(3分)
(2)证明∵CE平分∠ACD,
∴∠ECD=∠ECA,
∵∠ECD=∠B+∠E,∠BAC=∠ECA+∠E,
∴∠BAC=∠B+∠E+∠E=∠B+2∠E. …………………………(6分)
19.(每小题5分,共10分)
【解答】解:(1)2(x﹣5)(x+2)﹣(x﹣1)(2x+1),
=2(x2﹣3x﹣10)﹣(2x2﹣x﹣1)
=2x2﹣6x﹣20﹣2x2+x+1
=﹣5x﹣19, …………………………(3分)
当x=﹣2时,原式=﹣5×(﹣2)﹣19
=10﹣19
=﹣9; …………………………(5分)
(2)[(a+3b)(﹣a+3b)﹣(2a﹣3b)2﹣5a(a﹣4b)]÷(2a)
=[9b2﹣a2﹣(4a2﹣12ab+9b2)﹣5a2+20ab)÷(2a)
=(9b2﹣a2﹣4a2+12ab﹣9b2﹣5a2+20ab)÷(2a)
=(﹣10a2+32ab)÷2a
=﹣5a+16b, …………………………(3分)
当a=2,b时,原式=﹣5×2+16×()
=﹣10+(﹣8)
=﹣18. …………………………(5分)
20.(8分)
【解答】解:(1)如图,△A1B1C1即为所求, …………………………(3分)
(2)若B2(﹣4,2)与点B关于一条直线成轴对称,则此直线是y轴,
∴C(2,3)关于直线的对称点C2的坐标为(﹣2,3).
故答案为:(﹣2,3); …………………………(5分)
(3)△A1B1C1的面积为. …………………………(8分)
21.(8分)
【解答】解:(1)∵CE平分∠ACD,BE平分∠ABC,
∴,,
∵∠BAC=46°,
∴∠BAC=∠ACD﹣∠ABC=46°,
∴,
∵∠E=∠ECD﹣∠EBD,
∴∠E=23°; …………………………(4分)
(2)连接AE,作EF⊥AC于F,
∵BE平分∠ABC,EM⊥BC,EN⊥BA,
∴EM=EN,
同理,EF=EM,
∴EF=EN,
在Rt△FCE和Rt△MCE中,
,
∴Rt△FCE≌Rt△MCE(HL),
∴CF=CM=4,
同理,AF=AN=2,
∴AC=AF+CF=4+2=6. …………………………(4分)
22.(9分)
【解答】(1)证明:∵∠BAE+∠EAC=∠BAC,∠BAE+∠ABD=∠BDC,
又∵∠BAC=∠BFE,
∴∠BAE+∠EAC=∠BAE+∠ABD,
∴∠EAC=∠ABD; …………………………(3分)
(2)解:过点F作FG⊥BC于点G,如图所示:
∵AB=AC,
∴∠ABE=∠C,
∴∠BAC=180°﹣2∠ABE,
∴,
∴∠ABE+∠AEB=90°,
∴∠BAE=180°﹣90°=90°,
∴FA⊥AB,
∵BD平分∠ABC,FG⊥BC,
∴FG=AF=6,
∴; …………………………(3分)
(3)解:2AF=BF﹣EF;理由如下:
在BD上截取BH=AE,连接AH,如图所示:
在△ABH和△CAE中,
,
∴△ABH≌△CAE(SAS),
∴∠AHB=∠AEC,∠C=∠BAH,
∴,
根据解析(2)可知,∠BAE=90°,
∴∠HAF=90°﹣∠BAH=90°﹣∠C,
∴∠HAF=∠AHF,
∴AF=FH=BF﹣BH=BF﹣AE=BF﹣AF﹣EF,
∴2AF=BF﹣EF. …………………………(9分)
23.(10分)
【解答】解:(1)由图2知,阴影部分正方形的面积为(a+b)2﹣4ab=(a﹣b)2,
故答案为:(a+b)2﹣4ab=(a﹣b)2; …………………………(2分)
(2)∵(m+n)2=25,
∴m2+2mn+n2=25①,
∵(m﹣n)2=16,
∴m2﹣2mn+n2=16②,
①+②得:2(m2+n2)=41,
∴; …………………………(6分)
(3)设正方形ACDE的边长为x,正方形BCFG的边长为y,
∴x+y=7,x﹣y=3,
(x+y)2=(x﹣y)2+4xy,
∴72=32+4xy,
∴xy=10,
∴. …………………………(10分)
24.(12分)
【解答】解:(1)∵∠BAD=90°,∠BCA=90°,
∴∠1+∠2=90°,
∴∠B=90°﹣∠1=∠2,
∵BC⊥AC,DE⊥AC,
∴∠BCA=∠AED=90°,
∵AB=AD,
∴△ABC≌△DAE(AAS); …………………………(3分)
(2),理由如下, …………………………(4分)
作CE⊥y轴于点E,CD交y轴于点F,
∵∠BAC=90°,AB=AC,
同理可证△ABO≌△CAE,
∴AO=CE,S△ABO=S△CAE,
∵AO=AD,∠DAE=∠AEC=90°,
∴AO=CE=DA,AD∥CE,
∴∠ADF=∠ECF,
∴△ADF≌△ECF(ASA),
∴S△ADF=S△ECF,
∴S△ADC=S△ADF+S△AFC=S△ECF+S△AFC=S△AEC=S△ABO,
∴; …………………………(8分)
(3)点Q的坐标为(﹣4,8)或(﹣6,2)或(﹣2,4).
…………………………(12分)(写对一个得1分,2个3分).
(详解如下):①当∠POQ=90°时,过点P,Q分别作x轴的垂线,垂足分别为C,D,如图;
∵PO=QO,点P的坐标为(2,6),
同理可证△POD≌△OQC,
∴QC=OD=2,OC=PD=6,
∴点Q的坐标为(﹣6,2);
②当∠OPQ=90°时,作PD⊥x轴于点D,作QE⊥y轴于点F,交直线PD于点E,
∵PO=PQ,点P的坐标为(2,6),
同理可证△POD≌△QPE,
∴PE=OD=2,QE=PD=6,
∴QF=QE﹣EF=QE﹣OD=4,OF=ED=PE+PD=8,
∴点Q的坐标为(﹣4,8);
③当∠OQP=90°时,点Q的坐标为(﹣2,4).
综上,点Q的坐标为(﹣4,8)或(﹣6,2)或(﹣2,4).
第一部分(选择题 共30分)
一、选择题(本大题共10小题,每小题3分,满分30分.在每个小题给出的四个选项中,只有一项符合题目要求的)
1.下面四个手机应用图标中是轴对称图形的是( )
A. B. C. D.
2.下列各项计算结果是a8的是( )
A.a4 a2 B.a2+a4 C.(a3)5 D.a10÷a2
3.如图,将△ABC沿着平行于BC的直线DE折叠,点A落在点A'处,若∠B=44°,则∠A'DB的度数是( )
A.44° B.92° C.108° D.88°
4.下列运算正确的是( )
A.(﹣2a)2=﹣4a2 B.(a﹣b)2=a2﹣b2
C.(﹣m+2)(﹣m﹣2)=m2﹣4 D.(a5)2=a7
5.如图,△ABC中,BD平分∠ABC,EF垂直平分BC交BC于点E,交BD于点F,连接CF,若∠A=60°,∠ABD=25°,则∠ACF的度数为( )
A.25° B.45° C.50° D.70°
6.若(x2﹣px+q)(x﹣3)展开后不含x的一次项,则p与q的关系是( )
A.p=3q B.p+3q=0 C.q+3p=0 D.q=3p
7.如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CD于点D,BE⊥CD于点E.若BE=7,CE=3,则△ADE的面积是( )
A.6 B.21 C.12 D.24
8.已知2m﹣n=3,4m2﹣3mn+n2=14,则mn的值为( )
A.3 B.4 C.5 D.6
9.如图,在△ABC中,∠BAC=80°,边AB的垂直平分线交AB于点D,交BC于点E,边AC的垂直平分线交AC于点F,交BC于点G,连接AE,AG.则∠EAG的度数为( )
A.35° B.30° C.25° D.20°
10.如图,在△ABC中,AB=AC,BD为AC边上的高,BE平分∠ABD,点F在BD上,连接EF并延长交BC于点G,若BG=EG,∠A=2∠DEF,有下列结论:①∠DEF=∠CBD;②∠ABE+∠CBD=45°; ③EG⊥BC; ④BF=CE.其中正确的结论有( )
A.1个 B.4个 C.3个 D.2个
第二部分(选择题 共90分)
二、填空题(本大题共5小题,每小题3分,满分15分)
11.已知点A(a+3,5)与点B(5,b)关于y轴对称,则b﹣a的值是 .
12.如果x2+2(m﹣1)x+4是一个完全平方式,则m= .
13.一个正方形、一个正三角形和一个正五边形如图摆放,若∠3=34°,则∠1+∠2= °.
14.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=12cm,动点P从点A出发,沿AB向点B运动,动点Q从点B出发,沿BC向点C运动,如果动点P以2cm/s,Q以1cm/s的速度同时出发.设运动时间为t(s),P、Q在运动过程中,△PBQ的形状不断发生变化,当t 时,△PBQ是直角三角形.
15.如图,在Rt△ABC中,∠ACB=90°,BD平分∠ABC,E是AB上一点,且AE=AD,连接DE,过E作EF⊥BD,垂足为F,延长EF交BC于点G.现给出以下结论:①EF=FG;②CD=DE;③∠BEG=∠BDC;④∠DEF=45°.其中正确的是 .(写出所有正确结论的序号)
三、解答题(本大题共9小题,满分75分.解答应写出文字说明,证明过程或演算步骤)
16.(每小题3分,共6分)计算:
(1)a2 a4+(﹣2a2)3+a8÷a2; (2)y(3﹣4y)﹣(x+2y)(x﹣2y).
17.(每小题3分,共6分)因式分解:
(1) (a+1)2+2a(a+1). (2)25(m+n)2﹣9(m﹣n)2.
18.(6分)如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)若∠B=30°,∠BAC=130°,求∠E的度数;
(2)求证:∠BAC=∠B+2∠E.
19.(每小题5分,共10分)化简求值:
(1)2(x﹣5)(x+2)﹣(x﹣1)(2x+1),其中x=﹣2;
(2)[(a+3b)(﹣a+3b)﹣(2a﹣3b)2﹣5a(a﹣4b)]÷(2a),其中a=2,b.
20.(8分)如图所示,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,2),
C(2,3).
(1)在图中画出△ABC关于x轴对称的图形△A1B1C1;
(2)在图中,若B2(﹣4,2)与点B关于一条直线成轴对称,此时C点关于直线的对称点C2的坐标为 ;
(3)△A1B1C1的面积为 .
21.(8分)如图,在△ABC中,BE平分∠ABC,CE平分∠ACD.
(1)如图1,若∠A=46°,求∠E的度数;
(2)如图2,过点E作EM⊥BC,EN⊥BA,垂足分别为M,N,若AN=2,CM=4,求AC的长.
22.(9分)如图,在△ABC中,AB=AC,点D,E分别在边AC,BC上,连接AE,BD交于点F,∠BAC=∠BFE=2∠AEB.
(1)说明:∠EAC=∠ABD;
(2)若BD平分∠ABC,BE=15,AF=6,求△BEF的面积;
(3)判断EF,BF,AF之间的数量关系,并加以说明.
23.(10分)【综合实践】
图1是一个长为4b,宽为a(a>b)的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按如图2所示的形状拼成一个大正方形.
(1)观察图1,图2,请写出(a+b)2,(a﹣b)2,ab之间的等量关系是: ;
(2)已知(m+n)2=25,(m﹣n)2=16,求m2+n2的值;
(3)如图3,C是线段AB上的一点,以AC,BC为边向上分别作正方形ACDE和正方形BCFG,连接AF.若AB=7,DF=3,求△AFC的面积.
24.(12分)(1)如图1,∠BAD=90°,AB=AD,过点B作BC⊥AC于点C,过点D作DE⊥AC于点E.
求证:△ABC≌△DAE.
(2)如图2,等腰Rt△ABC中,∠BAC=90°,AB=AC,点A是y轴正半轴上的一动点,点B在x轴的正半轴上.以OA为直角边在y轴的左边作等腰Rt△OAD,AO=AD,连接CD,试问A点在运动过程中△AOB与△ACD面积的比值是否会发生变化?如果没有变化,请求出;若变化,请说明理由.
(3)如图3,在平面直角坐标系xOy中,点P的坐标为(2,6),点Q为第二象限内任一点.若△POQ是以OP为边的等腰直角三角形,请直接写出点Q的坐标.
参考答案
选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1 2 3 4 5 6 7 8 9 10
D D B C B C A C D B
二、填空题(本大题共5小题,每小题3分,共15分)
11.13 12.3或﹣1 13.
14.或6 15.①③④
三、解答题(本大题共9小题,满分75分.解答应写出文字说明,证明过程或演算步骤)
16.(每小题3分,共6分)
【解答】解:(1)a2 a4+(﹣2a2)3+a8÷a2
=a6﹣8a6+a6
=﹣6a6; …………………………(3分)
(2)y(3﹣4y)﹣(x+2y)(x﹣2y)
=3y﹣4y2﹣(x2﹣4y2)
=3y﹣4y2﹣x2+4y2
=3y﹣x2. …………………………(3分)
17.(每小题3分,共6分)
【解答】解:
(1)原式=(a+1)[(a+1)+2a]
=(a+1)(3a+1). …………………………(3分)
(2)原式=[5(m+n)]2﹣[3(m﹣n)]2
=(5m+5n)2﹣(3m﹣3n)2
=[(5m+5n)﹣(3m﹣3n)][(5m+5n)+(3m﹣3n)]
=(2m+8n)(8m+2n)
=4(m+4n)(4m+n); …………………………(3分)
18.(6分)
【解答】(1)解:∵∠B=30°,∠BAC=130°,
∴∠ACD=∠B+∠BAC=160°,
∵CE平分∠ACD,
∴∠ECD∠ACD=80°,
∴∠E=∠ECD﹣∠B=50°; …………………………(3分)
(2)证明∵CE平分∠ACD,
∴∠ECD=∠ECA,
∵∠ECD=∠B+∠E,∠BAC=∠ECA+∠E,
∴∠BAC=∠B+∠E+∠E=∠B+2∠E. …………………………(6分)
19.(每小题5分,共10分)
【解答】解:(1)2(x﹣5)(x+2)﹣(x﹣1)(2x+1),
=2(x2﹣3x﹣10)﹣(2x2﹣x﹣1)
=2x2﹣6x﹣20﹣2x2+x+1
=﹣5x﹣19, …………………………(3分)
当x=﹣2时,原式=﹣5×(﹣2)﹣19
=10﹣19
=﹣9; …………………………(5分)
(2)[(a+3b)(﹣a+3b)﹣(2a﹣3b)2﹣5a(a﹣4b)]÷(2a)
=[9b2﹣a2﹣(4a2﹣12ab+9b2)﹣5a2+20ab)÷(2a)
=(9b2﹣a2﹣4a2+12ab﹣9b2﹣5a2+20ab)÷(2a)
=(﹣10a2+32ab)÷2a
=﹣5a+16b, …………………………(3分)
当a=2,b时,原式=﹣5×2+16×()
=﹣10+(﹣8)
=﹣18. …………………………(5分)
20.(8分)
【解答】解:(1)如图,△A1B1C1即为所求, …………………………(3分)
(2)若B2(﹣4,2)与点B关于一条直线成轴对称,则此直线是y轴,
∴C(2,3)关于直线的对称点C2的坐标为(﹣2,3).
故答案为:(﹣2,3); …………………………(5分)
(3)△A1B1C1的面积为. …………………………(8分)
21.(8分)
【解答】解:(1)∵CE平分∠ACD,BE平分∠ABC,
∴,,
∵∠BAC=46°,
∴∠BAC=∠ACD﹣∠ABC=46°,
∴,
∵∠E=∠ECD﹣∠EBD,
∴∠E=23°; …………………………(4分)
(2)连接AE,作EF⊥AC于F,
∵BE平分∠ABC,EM⊥BC,EN⊥BA,
∴EM=EN,
同理,EF=EM,
∴EF=EN,
在Rt△FCE和Rt△MCE中,
,
∴Rt△FCE≌Rt△MCE(HL),
∴CF=CM=4,
同理,AF=AN=2,
∴AC=AF+CF=4+2=6. …………………………(4分)
22.(9分)
【解答】(1)证明:∵∠BAE+∠EAC=∠BAC,∠BAE+∠ABD=∠BDC,
又∵∠BAC=∠BFE,
∴∠BAE+∠EAC=∠BAE+∠ABD,
∴∠EAC=∠ABD; …………………………(3分)
(2)解:过点F作FG⊥BC于点G,如图所示:
∵AB=AC,
∴∠ABE=∠C,
∴∠BAC=180°﹣2∠ABE,
∴,
∴∠ABE+∠AEB=90°,
∴∠BAE=180°﹣90°=90°,
∴FA⊥AB,
∵BD平分∠ABC,FG⊥BC,
∴FG=AF=6,
∴; …………………………(3分)
(3)解:2AF=BF﹣EF;理由如下:
在BD上截取BH=AE,连接AH,如图所示:
在△ABH和△CAE中,
,
∴△ABH≌△CAE(SAS),
∴∠AHB=∠AEC,∠C=∠BAH,
∴,
根据解析(2)可知,∠BAE=90°,
∴∠HAF=90°﹣∠BAH=90°﹣∠C,
∴∠HAF=∠AHF,
∴AF=FH=BF﹣BH=BF﹣AE=BF﹣AF﹣EF,
∴2AF=BF﹣EF. …………………………(9分)
23.(10分)
【解答】解:(1)由图2知,阴影部分正方形的面积为(a+b)2﹣4ab=(a﹣b)2,
故答案为:(a+b)2﹣4ab=(a﹣b)2; …………………………(2分)
(2)∵(m+n)2=25,
∴m2+2mn+n2=25①,
∵(m﹣n)2=16,
∴m2﹣2mn+n2=16②,
①+②得:2(m2+n2)=41,
∴; …………………………(6分)
(3)设正方形ACDE的边长为x,正方形BCFG的边长为y,
∴x+y=7,x﹣y=3,
(x+y)2=(x﹣y)2+4xy,
∴72=32+4xy,
∴xy=10,
∴. …………………………(10分)
24.(12分)
【解答】解:(1)∵∠BAD=90°,∠BCA=90°,
∴∠1+∠2=90°,
∴∠B=90°﹣∠1=∠2,
∵BC⊥AC,DE⊥AC,
∴∠BCA=∠AED=90°,
∵AB=AD,
∴△ABC≌△DAE(AAS); …………………………(3分)
(2),理由如下, …………………………(4分)
作CE⊥y轴于点E,CD交y轴于点F,
∵∠BAC=90°,AB=AC,
同理可证△ABO≌△CAE,
∴AO=CE,S△ABO=S△CAE,
∵AO=AD,∠DAE=∠AEC=90°,
∴AO=CE=DA,AD∥CE,
∴∠ADF=∠ECF,
∴△ADF≌△ECF(ASA),
∴S△ADF=S△ECF,
∴S△ADC=S△ADF+S△AFC=S△ECF+S△AFC=S△AEC=S△ABO,
∴; …………………………(8分)
(3)点Q的坐标为(﹣4,8)或(﹣6,2)或(﹣2,4).
…………………………(12分)(写对一个得1分,2个3分).
(详解如下):①当∠POQ=90°时,过点P,Q分别作x轴的垂线,垂足分别为C,D,如图;
∵PO=QO,点P的坐标为(2,6),
同理可证△POD≌△OQC,
∴QC=OD=2,OC=PD=6,
∴点Q的坐标为(﹣6,2);
②当∠OPQ=90°时,作PD⊥x轴于点D,作QE⊥y轴于点F,交直线PD于点E,
∵PO=PQ,点P的坐标为(2,6),
同理可证△POD≌△QPE,
∴PE=OD=2,QE=PD=6,
∴QF=QE﹣EF=QE﹣OD=4,OF=ED=PE+PD=8,
∴点Q的坐标为(﹣4,8);
③当∠OQP=90°时,点Q的坐标为(﹣2,4).
综上,点Q的坐标为(﹣4,8)或(﹣6,2)或(﹣2,4).
同课章节目录
