4.1.1n次方根与分数指数幂 课件(共18张PPT)-高一上学期数学人教A版(2019)必修第一册
文档属性
| 名称 | 4.1.1n次方根与分数指数幂 课件(共18张PPT)-高一上学期数学人教A版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 17:48:51 | ||
图片预览






文档简介
(共18张PPT)
RJA
4.1.1 n次方根与分数指数幂
高中数学
必修第一册 RJ
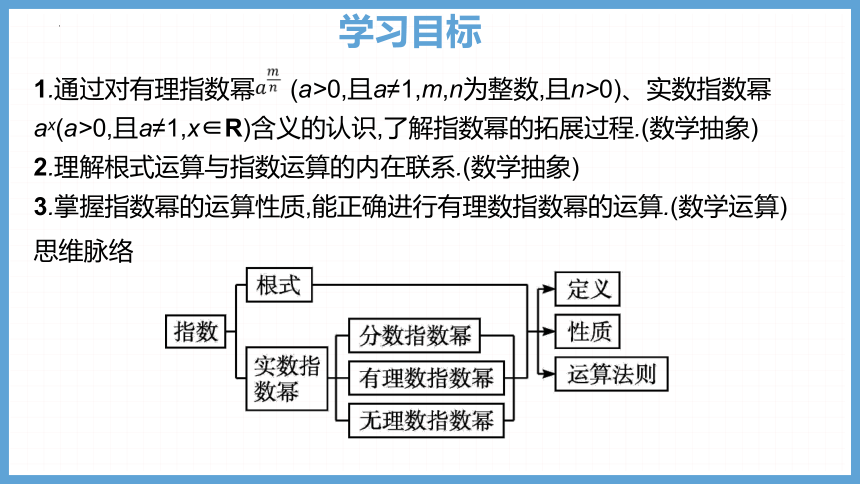
思维脉络
1.通过对有理指数幂 (a>0,且a≠1,m,n为整数,且n>0)、实数指数幂ax(a>0,且a≠1,x∈R)含义的认识,了解指数幂的拓展过程.(数学抽象)
2.理解根式运算与指数运算的内在联系.(数学抽象)
3.掌握指数幂的运算性质,能正确进行有理数指数幂的运算.(数学运算)
学习目标
希帕索斯
分数?
负整数或零
正整数
指数幂(幂)
公元前五世纪,古希腊有一个数学学派名为毕达哥拉斯学派,其学派中的一个成员希帕索斯考虑了一个问题:边长为1的正方形其对角线的长度是多少呢?他发现这一长度既不能用整数,也不能用分数来表示,希帕索斯的发现导致了数学史上第一个无理数的诞生——.
思考1.(1)16的平方根是什么?任何一个实数都有平方根吗?一个数
的平方根有几个?
(2) -27的立方根是什么?任何一个实数都有立方根吗?一个
数的立方根有几个?
(3)如果 x3=a,x4=b,x5=m,参照上面的说法,这里的x分
别叫什么名称?
(±4)2
= 16
±4是16的平方根
(-3) 3
= -27
-3是-27的立方根
x是a的立方根,
x是b的4次方根,
x是m的5次方根
新课导入
根式
根指数
被开方数
n次方根与根式
根式的运算性质
根据 次方根的意义,可得
问题 表示 的 次方根, 一定成立吗?
例题 求下列各式的值.
某种细胞分裂时,由1个分裂成2个,2个分裂成4个,
1个这样的细胞分裂x次后,得到的细胞个数y与x的
函数关系式是什么?
问题情境
分裂
次数
细胞
总数
1次
2次
3次
4次
x次
……
21
22
23
24
分数?
想一想
负整数或零
正整数
指数幂(幂)
根据n次方根的定义和数的运算,我们知道
思考:当被开方数的指数不能被根指数整除时,根式是否也可以表示为分数指数幂?
【定义】由此,我们规定,正数的正分数指数幂的意义是:
于是,在条件 下,根式都可以写成分数
指数幂的形式.正数的负分数指数幂的意义与负整数指数幂的意义相仿.
我们规定,
我们再规定,0的正分数指数幂等于0,0的负分数指数幂没意义.
新知讲解——分数指数幂
整数指数幂和分数指数幂统称有理数指数幂
整数指数幂的运算性质对于有理数指数幂也同样适用
有理数指数幂的运算性质
新知讲解——分数指数幂
例题 计算下列各式(式中字母全为正数):
-a
π-3
当堂检测(15分钟)
(1)
3.根式的性质:
1.n次方根的概念
2.根式的概念
(2)当n是奇数时,
当n是偶数时,
课堂小结
4.分数指数幂
RJA
4.1.1 n次方根与分数指数幂
高中数学
必修第一册 RJ
思维脉络
1.通过对有理指数幂 (a>0,且a≠1,m,n为整数,且n>0)、实数指数幂ax(a>0,且a≠1,x∈R)含义的认识,了解指数幂的拓展过程.(数学抽象)
2.理解根式运算与指数运算的内在联系.(数学抽象)
3.掌握指数幂的运算性质,能正确进行有理数指数幂的运算.(数学运算)
学习目标
希帕索斯
分数?
负整数或零
正整数
指数幂(幂)
公元前五世纪,古希腊有一个数学学派名为毕达哥拉斯学派,其学派中的一个成员希帕索斯考虑了一个问题:边长为1的正方形其对角线的长度是多少呢?他发现这一长度既不能用整数,也不能用分数来表示,希帕索斯的发现导致了数学史上第一个无理数的诞生——.
思考1.(1)16的平方根是什么?任何一个实数都有平方根吗?一个数
的平方根有几个?
(2) -27的立方根是什么?任何一个实数都有立方根吗?一个
数的立方根有几个?
(3)如果 x3=a,x4=b,x5=m,参照上面的说法,这里的x分
别叫什么名称?
(±4)2
= 16
±4是16的平方根
(-3) 3
= -27
-3是-27的立方根
x是a的立方根,
x是b的4次方根,
x是m的5次方根
新课导入
根式
根指数
被开方数
n次方根与根式
根式的运算性质
根据 次方根的意义,可得
问题 表示 的 次方根, 一定成立吗?
例题 求下列各式的值.
某种细胞分裂时,由1个分裂成2个,2个分裂成4个,
1个这样的细胞分裂x次后,得到的细胞个数y与x的
函数关系式是什么?
问题情境
分裂
次数
细胞
总数
1次
2次
3次
4次
x次
……
21
22
23
24
分数?
想一想
负整数或零
正整数
指数幂(幂)
根据n次方根的定义和数的运算,我们知道
思考:当被开方数的指数不能被根指数整除时,根式是否也可以表示为分数指数幂?
【定义】由此,我们规定,正数的正分数指数幂的意义是:
于是,在条件 下,根式都可以写成分数
指数幂的形式.正数的负分数指数幂的意义与负整数指数幂的意义相仿.
我们规定,
我们再规定,0的正分数指数幂等于0,0的负分数指数幂没意义.
新知讲解——分数指数幂
整数指数幂和分数指数幂统称有理数指数幂
整数指数幂的运算性质对于有理数指数幂也同样适用
有理数指数幂的运算性质
新知讲解——分数指数幂
例题 计算下列各式(式中字母全为正数):
-a
π-3
当堂检测(15分钟)
(1)
3.根式的性质:
1.n次方根的概念
2.根式的概念
(2)当n是奇数时,
当n是偶数时,
课堂小结
4.分数指数幂
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
