2.1.2两条直线平行和垂直的判定 课件(共15张PPT)-高二上学期数学人教版(2019)选择性必修第一册
文档属性
| 名称 | 2.1.2两条直线平行和垂直的判定 课件(共15张PPT)-高二上学期数学人教版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 20:11:17 | ||
图片预览






文档简介
(共15张PPT)
2.1直线的倾斜角与斜率
第二章 直线和圆的方程
课时2 两条直线平行和垂直的判定
新知探究
探究一:两条直线平行的判定
情境设置
问题1:如果两条直线中某条直线的斜率不存在,怎么判断它们的位置关系?
问题2:如何用斜率关系证明三点共线?
【解析】当直线的斜率不存在时,可以画图判断它们的位置关系.
【解析】对于 , , 三点,如果直线 的斜率等于直线 的斜率,它们有公共点 ,那么 , , 三点共线.
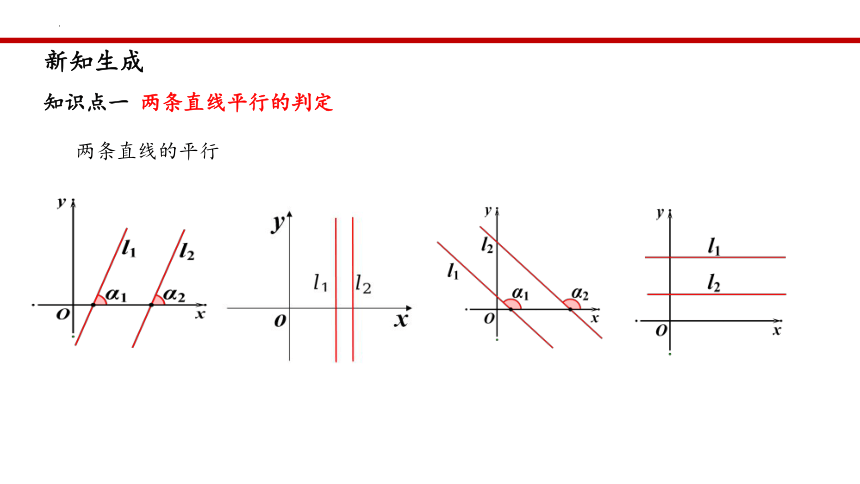
新知生成
知识点一 两条直线平行的判定
(1)两条直线都有斜率且不重合时的平行
设直线和的斜率分别为和,若它们平行,则它们的斜率相等,反之,若
它们不重合且斜率相等,则它们平行,即 (注意:该等价条件是在两条直线不重合且斜率存在的前提下才成立的,缺少这个前提,结论并不成立).
(2)特殊情况下的两条直线的平行
若两条平行直线中的一条直线的斜率不存在,则另一条直线的斜率也不存在,反之若两条不重合直线的斜率都不存在,则这两条直线平行.
特别提醒:讨论两条直线平行时,要分斜率存在和斜率不存在两种情形,缺少任
何一种情形都有可能发生错误.
新知生成
知识点一 两条直线平行的判定
两条直线的平行
一、两条直线平行的判定
例题1 根据下列给定的条件,判断直线与直线是否平行.
(1) 经过点,,经过点, ;
(2) 经过点,,经过点, ;
(3) 的倾斜角为 ,经过点, ;
(4) 平行于轴,经过点, .
【解析】(1)由题意知,,,所以直线与直线平行
或重合,又,所以 .
(2)由题意知,,,所以直线与直线平行或重合,又
,故直线与直线 重合.
(3)由题意知,,,,所以直线与直
线 平行或重合.
(4)由题意知,的斜率不存在,且不是轴,的斜率也不存在,恰好是轴,所以
.
反思感悟
方法总结
是针对斜率都存在且不重合的直线而言的,对于斜率不存在或
可能不存在的直线,要注意利用图形判断.
新知运用
跟踪训练1 (多选题)满足下列条件的直线与一定平行的是( ) .
A.经过点,,经过点,
B.的斜率为1,经过点,
C.经过点,,经过点,
D.经过点,,经过点,
CD
【解析】设直线的斜率为,直线的斜率为 .
对于A,,,,故与 不平行.
对于B,,,,故或与 重合.
对于C,,,则有.又 ,
则A,B,不共线.故 .
与均与轴垂直且不重合,故有 .
.
新知探究
探究二:两条直线垂直的判定
情境设置
问题1:如果两条直线垂直,那么这两条直线的方向向量具有怎样的关系?
问题2:斜率分别为, 的两条直线的方向向量分别是什么?
【解析】如果两条直线垂直,那么这两条直线的方向向量垂直.
【解析】 它们的方向向量分别为,.
新知生成
知识点二 两条直线垂直的判定
如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于____;反之,
如果它们的斜率之积等于____,那么它们互相垂直.即
特别提醒:成立的前提条件是两条直线的斜率都存在.
二、两条直线垂直的判定
例题2 判断下列各题中与是否垂直.
(1) 经过点,,经过点, ;
(2) 的一个方向向量为,经过点, ;
(3) 经过点,,经过点, .
【解析】(1) ,,,与 不垂直.
(2)由已知得,,, .
(3)由点,的横坐标相等,得的倾斜角为 ,则 轴.
,轴, .
反思感悟
方法总结
判断两条直线是否垂直的依据:在这两条直线都有斜率的前提下,只需看它
们的斜率之积是否等于 1即可,但应注意有一条直线与 轴垂直,另一条直线与 轴平行或重合时,这两条直线也垂直.
新知运用
跟踪训练2 (1)若不同的两点 , 的坐标分别为( , ),(3 ,3 ),且 + ≠3 ,则线段 的垂直平分线的斜率为____.
(2)已知△ 的顶点坐标分别为 (1,2), ( 1,1), (0,2),求 边上的高所在直线的斜率与倾斜角.
【解析】(1) 由过两点的直线的斜率公式可得,所以线段的垂直平分线
的斜率为 .
(2) 设边上的高所在直线的斜率为,则有 .
, ,
边上的高所在直线的斜率为,倾斜角为 .
随堂检测
1. 经过点 ( 2, )和 ( ,4)的直线平行于斜率等于1的直线,则实数 的值是( ) .
A.4 B.1
C.1或3 D.1或4
2. 过点,,的直线与过点,,的直线的位置关系为( ) .
A.垂直 B.平行
C.重合 D.以上都不正确
3.已知△ 中, (0,3), (2, 1), , 分别为 , 的中点,则直线 的斜率
为____.
B
A
随堂检测
4.当 为何值时,过两点 (1,1), 的直线:
(1)倾斜角为?
(2)与过两点(3,2),(0, 7) 的直线垂直?
(3)与过两点(2, 3),( 4,9) 的直线平行?
【解析】(1)由,解得或 .
(2),且,,解得或 .
(3) 令,解得或 .
课堂小结
1.知识清单:
(1)两条直线平行的判定;
(2)两条直线垂直的判定.
2.1直线的倾斜角与斜率
第二章 直线和圆的方程
课时2 两条直线平行和垂直的判定
新知探究
探究一:两条直线平行的判定
情境设置
问题1:如果两条直线中某条直线的斜率不存在,怎么判断它们的位置关系?
问题2:如何用斜率关系证明三点共线?
【解析】当直线的斜率不存在时,可以画图判断它们的位置关系.
【解析】对于 , , 三点,如果直线 的斜率等于直线 的斜率,它们有公共点 ,那么 , , 三点共线.
新知生成
知识点一 两条直线平行的判定
(1)两条直线都有斜率且不重合时的平行
设直线和的斜率分别为和,若它们平行,则它们的斜率相等,反之,若
它们不重合且斜率相等,则它们平行,即 (注意:该等价条件是在两条直线不重合且斜率存在的前提下才成立的,缺少这个前提,结论并不成立).
(2)特殊情况下的两条直线的平行
若两条平行直线中的一条直线的斜率不存在,则另一条直线的斜率也不存在,反之若两条不重合直线的斜率都不存在,则这两条直线平行.
特别提醒:讨论两条直线平行时,要分斜率存在和斜率不存在两种情形,缺少任
何一种情形都有可能发生错误.
新知生成
知识点一 两条直线平行的判定
两条直线的平行
一、两条直线平行的判定
例题1 根据下列给定的条件,判断直线与直线是否平行.
(1) 经过点,,经过点, ;
(2) 经过点,,经过点, ;
(3) 的倾斜角为 ,经过点, ;
(4) 平行于轴,经过点, .
【解析】(1)由题意知,,,所以直线与直线平行
或重合,又,所以 .
(2)由题意知,,,所以直线与直线平行或重合,又
,故直线与直线 重合.
(3)由题意知,,,,所以直线与直
线 平行或重合.
(4)由题意知,的斜率不存在,且不是轴,的斜率也不存在,恰好是轴,所以
.
反思感悟
方法总结
是针对斜率都存在且不重合的直线而言的,对于斜率不存在或
可能不存在的直线,要注意利用图形判断.
新知运用
跟踪训练1 (多选题)满足下列条件的直线与一定平行的是( ) .
A.经过点,,经过点,
B.的斜率为1,经过点,
C.经过点,,经过点,
D.经过点,,经过点,
CD
【解析】设直线的斜率为,直线的斜率为 .
对于A,,,,故与 不平行.
对于B,,,,故或与 重合.
对于C,,,则有.又 ,
则A,B,不共线.故 .
与均与轴垂直且不重合,故有 .
.
新知探究
探究二:两条直线垂直的判定
情境设置
问题1:如果两条直线垂直,那么这两条直线的方向向量具有怎样的关系?
问题2:斜率分别为, 的两条直线的方向向量分别是什么?
【解析】如果两条直线垂直,那么这两条直线的方向向量垂直.
【解析】 它们的方向向量分别为,.
新知生成
知识点二 两条直线垂直的判定
如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于____;反之,
如果它们的斜率之积等于____,那么它们互相垂直.即
特别提醒:成立的前提条件是两条直线的斜率都存在.
二、两条直线垂直的判定
例题2 判断下列各题中与是否垂直.
(1) 经过点,,经过点, ;
(2) 的一个方向向量为,经过点, ;
(3) 经过点,,经过点, .
【解析】(1) ,,,与 不垂直.
(2)由已知得,,, .
(3)由点,的横坐标相等,得的倾斜角为 ,则 轴.
,轴, .
反思感悟
方法总结
判断两条直线是否垂直的依据:在这两条直线都有斜率的前提下,只需看它
们的斜率之积是否等于 1即可,但应注意有一条直线与 轴垂直,另一条直线与 轴平行或重合时,这两条直线也垂直.
新知运用
跟踪训练2 (1)若不同的两点 , 的坐标分别为( , ),(3 ,3 ),且 + ≠3 ,则线段 的垂直平分线的斜率为____.
(2)已知△ 的顶点坐标分别为 (1,2), ( 1,1), (0,2),求 边上的高所在直线的斜率与倾斜角.
【解析】(1) 由过两点的直线的斜率公式可得,所以线段的垂直平分线
的斜率为 .
(2) 设边上的高所在直线的斜率为,则有 .
, ,
边上的高所在直线的斜率为,倾斜角为 .
随堂检测
1. 经过点 ( 2, )和 ( ,4)的直线平行于斜率等于1的直线,则实数 的值是( ) .
A.4 B.1
C.1或3 D.1或4
2. 过点,,的直线与过点,,的直线的位置关系为( ) .
A.垂直 B.平行
C.重合 D.以上都不正确
3.已知△ 中, (0,3), (2, 1), , 分别为 , 的中点,则直线 的斜率
为____.
B
A
随堂检测
4.当 为何值时,过两点 (1,1), 的直线:
(1)倾斜角为?
(2)与过两点(3,2),(0, 7) 的直线垂直?
(3)与过两点(2, 3),( 4,9) 的直线平行?
【解析】(1)由,解得或 .
(2),且,,解得或 .
(3) 令,解得或 .
课堂小结
1.知识清单:
(1)两条直线平行的判定;
(2)两条直线垂直的判定.
