2024-2025学年湖南省衡阳市衡阳县第一中学高三(上)期中物理试卷(含答案)
文档属性
| 名称 | 2024-2025学年湖南省衡阳市衡阳县第一中学高三(上)期中物理试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 585.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-12-07 17:12:19 | ||
图片预览




文档简介
2024-2025学年湖南省衡阳市衡阳县第一中学高三(上)期中物理试卷
一、单选题:本大题共7小题,共28分。
1.在如图所示的照片中,关于物体或人在运动过程中的一些描述正确的是( )
A. 甲图是一列在::之间由厦门北开往武汉的动车,:是指动车运动的时间间隔
B. 乙图中的电风扇在断电后会慢慢停下,原因是断电后电动机不再提供动力,失去动力导致扇叶停下
C. 丙图中运动员在跑步比赛,起跑时,地面对运动员的作用力大于运动员对地面的作用力,因此运动员才能加速启动
D. 丁图是正在做精彩表演的芭蕾舞演员,台下的观众不可以把她们视为质点
2.年月日,巴黎奥运会跳水女子双人米跳台决赛,中国选手全红婵、陈芋汐完美展现“水花消失术”,以绝对优势获得金牌,跳水过程从离开跳板开始计时,图像如下图所示,图中仅段为直线,不计空气阻力,则由图可知( )
A. 段运动员处于失重状态
B. 段为空中的运动时间,该段时间运动员的速度方向始终竖直向下
C. 段运动员的加速度逐渐增大
D. 段运动员一直处于超重状态
3.如图所示,配有调节倾角的简易支架放在水平桌面上,上语文课时,某同学将一本古汉语字典放在支架的斜面上,若字典与支架斜面间的动摩擦因数为,设最大静摩擦力等于滑动摩擦力,缓慢地调节倾角使得字典与支架始终处于静止状态,则下列说法正确的是( )
A. 倾角增大,字典受到的支持力增大
B. 倾角增大,字典受到的摩擦力减小
C. 若字典始终处于静止状态,支架对字典的作用力不变
D. 若字典始终处于静止状态,支架倾角的最大值
4.如图,不可伸长的轻绳绕过光滑的钉子,一端固定在地面上,另一端吊着一个小球。在钉子沿水平方向向左匀速运动的过程中,下列说法正确的是( )
A. 小球在竖直方向上做加速运动 B. 小球在竖直方向上做减速运动
C. 小球在竖直方向上做匀速运动 D. 小球的运动轨迹是一条倾斜直线
5.如图所示,在距地面同一高度处将三个相同的小球以相同的速率分别沿竖直向下、竖直向上、水平向右的方向抛出,不计空气阻力,比较这三个小球从抛出到落地的过程,下列说法正确的是( )
A. 重力对每个小球做的功都各不相同
B. 重力对每个小球的冲量都各不相同
C. 每个小球落地时的速度都各不相同
D. 每个小球落地时重力做功的瞬时功率都各不相同
6.与地球公转轨道“外切”的小行星甲和“内切”的小行星乙的公转轨道如图所示,假设这些小行星与地球的公转轨道都在同一平面内,已知地球的公转半径为,公转周期为,小行星甲的远日点到太阳的距离为,小行星乙的近日点到太阳的距离为,引力常量为,下列说法正确的是( )
A. 小行星甲与太阳的连线和小行星乙与太阳的连线在相同时间内扫过的面积相等
B. 小行星乙在远日点的加速度大小等于地球公转的加速度大小
C. 小行星甲的公转周期为
D. 太阳的密度为
7.水平地面上有一质量为半球型碗,内表面光滑,质量的小球从边缘由静止滚到底端的过程,碗一直保持静止,取重力加速度为在此过程中( )
A. 底座受到地面的最大摩擦力为
B. 底座对地面的最大压力为
C. 底座与地面的动摩擦因数最小为
D. 如果把碗放在光滑的水平面上,小球不能到达碗的另一侧边缘
二、多选题:本大题共3小题,共18分。
8.多选年月日,千帆极轨组卫星一箭星发射升空,此次发射的千帆极轨组卫星是我国低轨“千帆星座”的首批组网星,卫星运行的轨道高度距地面约到,已知地球半径约为,引力常量,同步卫星的轨道距地面高度约为,运行周期,卫星是组中轨道最低的,卫星是组中轨道最高的,下列说法正确的是
A. 卫星的运行周期约为 B. 、卫星的运行周期之比约为
C. 根据以上信息可以求出地球的质量 D. 千帆极轨组卫星的发射速度大于
9.某高速公路上,由于前车违规停车发生一起追尾交通事故,图乙所示为交警根据现场测量绘制的刹车痕迹勘察示意图,其中表示前后两车减速区域重叠部分的长度。将后车制动过程和碰后两车的减速过程均视为匀减速直线运动,两车均视为质点且质量相等,所受阻力大小均始终为车重的倍,碰撞时间极短,且碰撞前后两车始终在同一直线上运动,该高速路段的限速为,重力加速度。下列说法正确的是( )
A. 两车碰后瞬间前车的速度为 B. 两车碰后瞬间后车的速度为
C. 后车刹车后,经停下来 D. 后车开始刹车时,没有超速
10.如图所示,轻杆一端可绕光滑铰链在竖直平面内自由转动,另一端固定一可视为质点的小球;轻绳一
端连接小球,另一端穿过位于点正下方的小孔与相连。用沿绳斜向上的拉力作用于小球,使杆保持水平。某时刻撤去拉力,小球、带动轻杆绕点转动。已知小球、的质量均为,杆长为,长为,重力加速度为,忽略一切阻力。则下列说法正确的是( )
A. 杆保持水平时,轻杆对小球的拉力大小为
B. 运动过程中,两小球速度大小相等时的速度值为
C. 运动过程中,两小球速度大小相等时细绳对小球的拉力大小为
D. 运动过程中,两小球速度大小相等时轻杆对小球的拉力大小为
三、实验题:本大题共2小题,共14分。
11.某同学利用如图所示的装置进行探究物体之间拉力的关系。质量为、的物块、放在左端固定有光滑定滑轮的长木板上,两物块左端分别固定有拉力传感器、,拉力传感器质量不计。物块与拉力传感器通过轻绳连接,拉力传感器通过绕过定滑轮的轻绳与装有砝码的砝码盘连接。现将纸带穿过打点计时器与物块连接。实验过程中轻绳、纸带均与长木板平行,拉力传感器、对应的示数分别为、。
以物块和作为研究对象,探究加速度和拉力之间的关系。关于实验过程,下列说法正确的是_____。
A.实验过程中需要补偿阻力
B.实验过程中应先释放物块、后接通打点计时器的电源
C.实验过程中需要保证砝码和砝码盘的质量远小于两物块的总质量
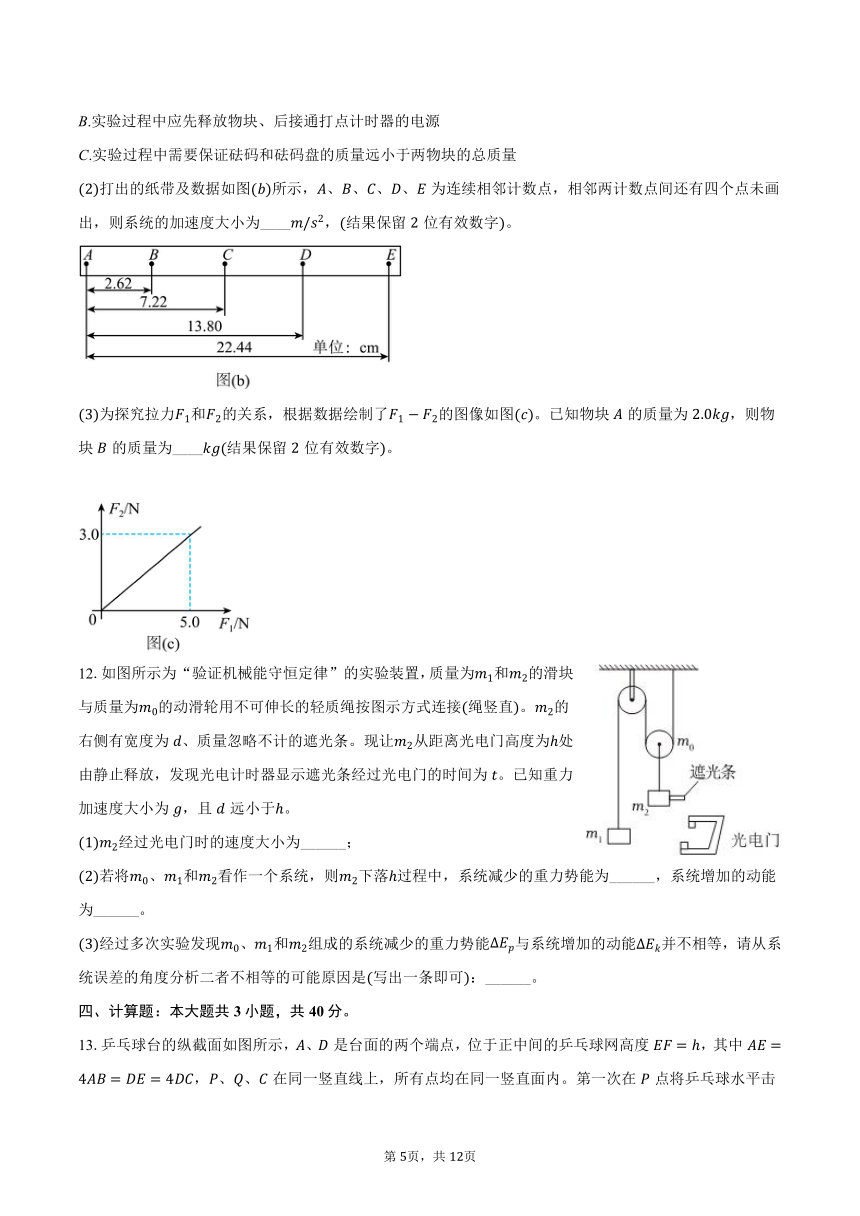
打出的纸带及数据如图所示,、、、、为连续相邻计数点,相邻两计数点间还有四个点未画出,则系统的加速度大小为____,结果保留位有效数字。
为探究拉力和的关系,根据数据绘制了的图像如图。已知物块的质量为,则物块的质量为____结果保留位有效数字。
12.如图所示为“验证机械能守恒定律”的实验装置,质量为和的滑块与质量为的动滑轮用不可伸长的轻质绳按图示方式连接绳竖直。的右侧有宽度为、质量忽略不计的遮光条。现让从距离光电门高度为处由静止释放,发现光电计时器显示遮光条经过光电门的时间为。已知重力加速度大小为,且远小于。
经过光电门时的速度大小为______;
若将、和看作一个系统,则下落过程中,系统减少的重力势能为______,系统增加的动能为______。
经过多次实验发现、和组成的系统减少的重力势能与系统增加的动能并不相等,请从系统误差的角度分析二者不相等的可能原因是写出一条即可:______。
四、计算题:本大题共3小题,共40分。
13.乒乓球台的纵截面如图所示,、是台面的两个端点,位于正中间的乒乓球网高度,其中,、、在同一竖直线上,所有点均在同一竖直面内。第一次在点将乒乓球水平击出,球恰好过球网的最高点,且刚好落到点;第二次在点将同一乒乓球斜向上击出,轨迹的最高点恰好过球网最高点,同时落在点。乒乓球可看做质点,不计空气阻力作用。求:注意:计算题中二级结论不能直接使用
点到台面的高度;
点到台面的高度。
14.汽车以某一速度在平直公路上匀速行驶,行驶过程中司机忽然发现前方处有一警示牌,立即刹车。刹车过程中,汽车加速度的大小随位移变化的关系如图所示。司机的反应时间,在这段时间内汽车仍保持匀速行驶,段为刹车系统的启动阶段,从位置开始,汽车的刹车系统稳定工作,直至汽车停止。已知从位置开始计时,汽车第内的位移为,第内的位移为。
求汽车刹车系统稳定工作后加速度的大小及位置汽车的速度大小;
若段位移大小为,求从司机发现警示牌到汽车停止过程汽车位移的大小。
15.如图所示,长的水平传送带沿逆时针方向转动,带速大小可以根据需要进行调节,传送带左右两侧光滑平台等高,左侧平台上固定着一个半径的光滑圆弧轨道和光滑圆轨道,两轨道间的平台足够长,点为圆轨道内侧最高点,最低点、点相互靠近且错开,右侧竖直墙壁上固定一个轻质弹簧。质量的物块从圆弧轨道的最高点由静止释放,与静止在轨道最低点的质量的物块发生弹性碰撞,碰后撤去圆弧轨道。已知物块与传送带间的动摩擦因数,重力加速度,物块、均可看作质点。
物块、第一次碰撞后,求物块的速度大小;
若两物块碰撞后只有物块能通过圆轨道的最高点且物块、均不脱轨:
求圆轨道半径的范围;
若中间圆轨道的半径为,当传送带沿逆时针转动的速度由增加至某一值时,保持此值不变,将仍从点由静止释放后,物块恰好与物块发生第二次弹性碰撞,求物块与传送带组成的系统先后两次因摩擦产生的热量之比。
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12. 定滑轮有质量或旋转增加了动能或存在摩擦或存在阻力
13.第一次在点将乒乓球水平击出,乒乓球做平抛运动,由 ,可知
由于平抛运动在水平方向做匀速直线运动,由 ,可知乒乓球从到的时间 与乒乓球从到的时间 相等,即
乒乓球在竖直方向上做自由落体运动,由
, ,
解得点到台面的高度
第二次在点将同一乒乓球斜向上击出,乒乓球做斜抛运动,乒乓球在水平方向上做匀速直线运动,由 ,可得
由 ,可得
乒乓球由到的运动为平抛运动,乒乓球从到的运动可看作逆向的平抛运动,竖直方向上是自由落体运动,则
,
解得点到台面的高度
14.假设第三秒内未停止,则加速度大小为
最后一秒内的位移应为
假设成立。
根据匀变速直线运动规律
解得
从,取一小段位移 ,则有
上式相加有
其中括号内之和表示 图像围成面积,可得
解得
则反应时间内
在匀减速阶段有
汽车行驶总位移
15.从点下滑到圆弧轨道最低点的过程,由机械能守恒定律
解得第一次与碰前速度大小
对、第一次弹性碰撞过程,由机械能守恒定律
由动量守恒定律
解得
,
若刚好能通过最高点,有
从点运动到最高点,由动能定理
解得
运动到与圆轨道的圆心等高处,速度减为零,恰好不脱轨,由动能定理
,
解得
则圆轨道半径范围
反弹后向左运动时,要想与碰撞,首先要通过圆轨道最高点,则
从最高点沿圆轨道滑下,到达底端,设其速度为,由动能定理
解得
从点向右运动到点,设在点的速度为,由动能定理
解得
反弹后,若从点一直减速运动到点,设在点的速度为,有
解得
由上式可知,当传送带速度传时,向左运动,既能通过传送带,又能通过最高点,之后恰好与发生第次弹性碰撞。
向右运动过程中,相对传送带滑动的时间
与传送带的相对位移
向左运动过程中,相对传送带滑动的时间
与传送带的相对位移
由于与传送带因摩擦产生的热量
故
第1页,共1页
一、单选题:本大题共7小题,共28分。
1.在如图所示的照片中,关于物体或人在运动过程中的一些描述正确的是( )
A. 甲图是一列在::之间由厦门北开往武汉的动车,:是指动车运动的时间间隔
B. 乙图中的电风扇在断电后会慢慢停下,原因是断电后电动机不再提供动力,失去动力导致扇叶停下
C. 丙图中运动员在跑步比赛,起跑时,地面对运动员的作用力大于运动员对地面的作用力,因此运动员才能加速启动
D. 丁图是正在做精彩表演的芭蕾舞演员,台下的观众不可以把她们视为质点
2.年月日,巴黎奥运会跳水女子双人米跳台决赛,中国选手全红婵、陈芋汐完美展现“水花消失术”,以绝对优势获得金牌,跳水过程从离开跳板开始计时,图像如下图所示,图中仅段为直线,不计空气阻力,则由图可知( )
A. 段运动员处于失重状态
B. 段为空中的运动时间,该段时间运动员的速度方向始终竖直向下
C. 段运动员的加速度逐渐增大
D. 段运动员一直处于超重状态
3.如图所示,配有调节倾角的简易支架放在水平桌面上,上语文课时,某同学将一本古汉语字典放在支架的斜面上,若字典与支架斜面间的动摩擦因数为,设最大静摩擦力等于滑动摩擦力,缓慢地调节倾角使得字典与支架始终处于静止状态,则下列说法正确的是( )
A. 倾角增大,字典受到的支持力增大
B. 倾角增大,字典受到的摩擦力减小
C. 若字典始终处于静止状态,支架对字典的作用力不变
D. 若字典始终处于静止状态,支架倾角的最大值
4.如图,不可伸长的轻绳绕过光滑的钉子,一端固定在地面上,另一端吊着一个小球。在钉子沿水平方向向左匀速运动的过程中,下列说法正确的是( )
A. 小球在竖直方向上做加速运动 B. 小球在竖直方向上做减速运动
C. 小球在竖直方向上做匀速运动 D. 小球的运动轨迹是一条倾斜直线
5.如图所示,在距地面同一高度处将三个相同的小球以相同的速率分别沿竖直向下、竖直向上、水平向右的方向抛出,不计空气阻力,比较这三个小球从抛出到落地的过程,下列说法正确的是( )
A. 重力对每个小球做的功都各不相同
B. 重力对每个小球的冲量都各不相同
C. 每个小球落地时的速度都各不相同
D. 每个小球落地时重力做功的瞬时功率都各不相同
6.与地球公转轨道“外切”的小行星甲和“内切”的小行星乙的公转轨道如图所示,假设这些小行星与地球的公转轨道都在同一平面内,已知地球的公转半径为,公转周期为,小行星甲的远日点到太阳的距离为,小行星乙的近日点到太阳的距离为,引力常量为,下列说法正确的是( )
A. 小行星甲与太阳的连线和小行星乙与太阳的连线在相同时间内扫过的面积相等
B. 小行星乙在远日点的加速度大小等于地球公转的加速度大小
C. 小行星甲的公转周期为
D. 太阳的密度为
7.水平地面上有一质量为半球型碗,内表面光滑,质量的小球从边缘由静止滚到底端的过程,碗一直保持静止,取重力加速度为在此过程中( )
A. 底座受到地面的最大摩擦力为
B. 底座对地面的最大压力为
C. 底座与地面的动摩擦因数最小为
D. 如果把碗放在光滑的水平面上,小球不能到达碗的另一侧边缘
二、多选题:本大题共3小题,共18分。
8.多选年月日,千帆极轨组卫星一箭星发射升空,此次发射的千帆极轨组卫星是我国低轨“千帆星座”的首批组网星,卫星运行的轨道高度距地面约到,已知地球半径约为,引力常量,同步卫星的轨道距地面高度约为,运行周期,卫星是组中轨道最低的,卫星是组中轨道最高的,下列说法正确的是
A. 卫星的运行周期约为 B. 、卫星的运行周期之比约为
C. 根据以上信息可以求出地球的质量 D. 千帆极轨组卫星的发射速度大于
9.某高速公路上,由于前车违规停车发生一起追尾交通事故,图乙所示为交警根据现场测量绘制的刹车痕迹勘察示意图,其中表示前后两车减速区域重叠部分的长度。将后车制动过程和碰后两车的减速过程均视为匀减速直线运动,两车均视为质点且质量相等,所受阻力大小均始终为车重的倍,碰撞时间极短,且碰撞前后两车始终在同一直线上运动,该高速路段的限速为,重力加速度。下列说法正确的是( )
A. 两车碰后瞬间前车的速度为 B. 两车碰后瞬间后车的速度为
C. 后车刹车后,经停下来 D. 后车开始刹车时,没有超速
10.如图所示,轻杆一端可绕光滑铰链在竖直平面内自由转动,另一端固定一可视为质点的小球;轻绳一
端连接小球,另一端穿过位于点正下方的小孔与相连。用沿绳斜向上的拉力作用于小球,使杆保持水平。某时刻撤去拉力,小球、带动轻杆绕点转动。已知小球、的质量均为,杆长为,长为,重力加速度为,忽略一切阻力。则下列说法正确的是( )
A. 杆保持水平时,轻杆对小球的拉力大小为
B. 运动过程中,两小球速度大小相等时的速度值为
C. 运动过程中,两小球速度大小相等时细绳对小球的拉力大小为
D. 运动过程中,两小球速度大小相等时轻杆对小球的拉力大小为
三、实验题:本大题共2小题,共14分。
11.某同学利用如图所示的装置进行探究物体之间拉力的关系。质量为、的物块、放在左端固定有光滑定滑轮的长木板上,两物块左端分别固定有拉力传感器、,拉力传感器质量不计。物块与拉力传感器通过轻绳连接,拉力传感器通过绕过定滑轮的轻绳与装有砝码的砝码盘连接。现将纸带穿过打点计时器与物块连接。实验过程中轻绳、纸带均与长木板平行,拉力传感器、对应的示数分别为、。
以物块和作为研究对象,探究加速度和拉力之间的关系。关于实验过程,下列说法正确的是_____。
A.实验过程中需要补偿阻力
B.实验过程中应先释放物块、后接通打点计时器的电源
C.实验过程中需要保证砝码和砝码盘的质量远小于两物块的总质量
打出的纸带及数据如图所示,、、、、为连续相邻计数点,相邻两计数点间还有四个点未画出,则系统的加速度大小为____,结果保留位有效数字。
为探究拉力和的关系,根据数据绘制了的图像如图。已知物块的质量为,则物块的质量为____结果保留位有效数字。
12.如图所示为“验证机械能守恒定律”的实验装置,质量为和的滑块与质量为的动滑轮用不可伸长的轻质绳按图示方式连接绳竖直。的右侧有宽度为、质量忽略不计的遮光条。现让从距离光电门高度为处由静止释放,发现光电计时器显示遮光条经过光电门的时间为。已知重力加速度大小为,且远小于。
经过光电门时的速度大小为______;
若将、和看作一个系统,则下落过程中,系统减少的重力势能为______,系统增加的动能为______。
经过多次实验发现、和组成的系统减少的重力势能与系统增加的动能并不相等,请从系统误差的角度分析二者不相等的可能原因是写出一条即可:______。
四、计算题:本大题共3小题,共40分。
13.乒乓球台的纵截面如图所示,、是台面的两个端点,位于正中间的乒乓球网高度,其中,、、在同一竖直线上,所有点均在同一竖直面内。第一次在点将乒乓球水平击出,球恰好过球网的最高点,且刚好落到点;第二次在点将同一乒乓球斜向上击出,轨迹的最高点恰好过球网最高点,同时落在点。乒乓球可看做质点,不计空气阻力作用。求:注意:计算题中二级结论不能直接使用
点到台面的高度;
点到台面的高度。
14.汽车以某一速度在平直公路上匀速行驶,行驶过程中司机忽然发现前方处有一警示牌,立即刹车。刹车过程中,汽车加速度的大小随位移变化的关系如图所示。司机的反应时间,在这段时间内汽车仍保持匀速行驶,段为刹车系统的启动阶段,从位置开始,汽车的刹车系统稳定工作,直至汽车停止。已知从位置开始计时,汽车第内的位移为,第内的位移为。
求汽车刹车系统稳定工作后加速度的大小及位置汽车的速度大小;
若段位移大小为,求从司机发现警示牌到汽车停止过程汽车位移的大小。
15.如图所示,长的水平传送带沿逆时针方向转动,带速大小可以根据需要进行调节,传送带左右两侧光滑平台等高,左侧平台上固定着一个半径的光滑圆弧轨道和光滑圆轨道,两轨道间的平台足够长,点为圆轨道内侧最高点,最低点、点相互靠近且错开,右侧竖直墙壁上固定一个轻质弹簧。质量的物块从圆弧轨道的最高点由静止释放,与静止在轨道最低点的质量的物块发生弹性碰撞,碰后撤去圆弧轨道。已知物块与传送带间的动摩擦因数,重力加速度,物块、均可看作质点。
物块、第一次碰撞后,求物块的速度大小;
若两物块碰撞后只有物块能通过圆轨道的最高点且物块、均不脱轨:
求圆轨道半径的范围;
若中间圆轨道的半径为,当传送带沿逆时针转动的速度由增加至某一值时,保持此值不变,将仍从点由静止释放后,物块恰好与物块发生第二次弹性碰撞,求物块与传送带组成的系统先后两次因摩擦产生的热量之比。
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12. 定滑轮有质量或旋转增加了动能或存在摩擦或存在阻力
13.第一次在点将乒乓球水平击出,乒乓球做平抛运动,由 ,可知
由于平抛运动在水平方向做匀速直线运动,由 ,可知乒乓球从到的时间 与乒乓球从到的时间 相等,即
乒乓球在竖直方向上做自由落体运动,由
, ,
解得点到台面的高度
第二次在点将同一乒乓球斜向上击出,乒乓球做斜抛运动,乒乓球在水平方向上做匀速直线运动,由 ,可得
由 ,可得
乒乓球由到的运动为平抛运动,乒乓球从到的运动可看作逆向的平抛运动,竖直方向上是自由落体运动,则
,
解得点到台面的高度
14.假设第三秒内未停止,则加速度大小为
最后一秒内的位移应为
假设成立。
根据匀变速直线运动规律
解得
从,取一小段位移 ,则有
上式相加有
其中括号内之和表示 图像围成面积,可得
解得
则反应时间内
在匀减速阶段有
汽车行驶总位移
15.从点下滑到圆弧轨道最低点的过程,由机械能守恒定律
解得第一次与碰前速度大小
对、第一次弹性碰撞过程,由机械能守恒定律
由动量守恒定律
解得
,
若刚好能通过最高点,有
从点运动到最高点,由动能定理
解得
运动到与圆轨道的圆心等高处,速度减为零,恰好不脱轨,由动能定理
,
解得
则圆轨道半径范围
反弹后向左运动时,要想与碰撞,首先要通过圆轨道最高点,则
从最高点沿圆轨道滑下,到达底端,设其速度为,由动能定理
解得
从点向右运动到点,设在点的速度为,由动能定理
解得
反弹后,若从点一直减速运动到点,设在点的速度为,有
解得
由上式可知,当传送带速度传时,向左运动,既能通过传送带,又能通过最高点,之后恰好与发生第次弹性碰撞。
向右运动过程中,相对传送带滑动的时间
与传送带的相对位移
向左运动过程中,相对传送带滑动的时间
与传送带的相对位移
由于与传送带因摩擦产生的热量
故
第1页,共1页
同课章节目录
