2024-2025学年人教版七年级数学上册5.2 第二课时 解一元一次方程——移项 课件(共24张PPT)
文档属性
| 名称 | 2024-2025学年人教版七年级数学上册5.2 第二课时 解一元一次方程——移项 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 282.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 10:30:52 | ||
图片预览








文档简介
版本:人教版
年级:七年级上册
数学
第五章 一元一次方程
5.2 解一元一次方程
第二课时 解一元一次方程——移项
学习目标
1. 理解移项的意义,掌握移项的方法.(重点)
2. 学会运用移项解形如“ax+b=cx+d”的一元一
次方程.(重点)
3. 能够抓住实际问题中的数量关系列一元一次方
程解决实际问题.(难点)
1. 解方程:
2. 观察下列一元一次方程,与上题的类型有什么区别?
怎样才能使它向 x=a (a为常数)的形式转化呢?
温故知新
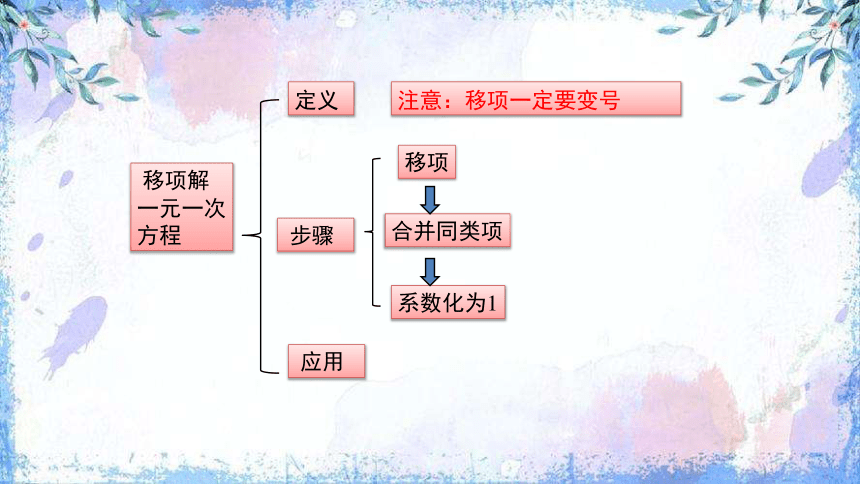
一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
移项的定义
注意:移项一定要变号
移项的依据及注意事项
移项实际上是利用等式的性质1.
易错提醒:
移项是方程中的某一项从方程的一边移到另一边,不要将其与加法的交换律或等式的性质2弄混淆.
解一元一次方程ax+b=cx+d(a,b,c,d均为常数,且a≠c)的一般步骤:
知识要点
ax-cx=d-b
移项
合并同类项
系数化为1
(a-c)x=d-b
移项解一元一次方程
定义
步骤
应用
注意:移项一定要变号
移项
合并同类项
系数化为1
让学习变的简单
PART 01
温故知新
温故知新
课堂导学
核心素养分层练
1.把等式一边的某项 后移到另一边,叫作移项.
2.方程3x=2x+1的解是( )
A.x=-1 B.x=1 C.x= D.x=-
变号
B
知识点:移项
1.若2m-3=3n+1,则2m-3n= .
2.方程3x+7=4x+5的解为x= .
3.若式子5x-7与4x+9的值相等,则x的值是 .
4
2
16
4.若x=-是方程2x-cx=-3+c的解,则c的值为(C)
A.-2 B.- C. D.2
5.王博在做课外习题时遇到如图所示的一道题,其中 是被污损而看不清的一个数,他翻看答案后得知该题的计算结果为15,则 表示的数是( )
A.10 B.-4
C.-10 D.10或-4
A
6.我国古代数学著作《增删算法统宗》记载了“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.”其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,则符合题意的方程是( )
A.2x+5=x+5 B.2x-5=x-5
C.x+5=x+5 D.x+5=x-5
D
1.方程3x=2x+7的解是( )
A.x=4
B.x=-4
C.x=7
D.x=-7
C
2.若x+1的值为6,则x等于( )
A.5 B.-5
C.7 D.-7
3.一元一次方程2x-8=0的解是x= .
4.当x= 时,式子2x-1的值比式子5x+6的值小1.
5.若m+1与-2互为相反数,则m的值为 .
A
4
-2
1
6.下列方程变形中,移项正确的是( )
A.由x+3=6,得x=6+3
B.由2x=x+1,得x-2x=1
C.由-2y=12-y,得y-2y=12
D.由x+5=1-2x,得x-2x=1+5
C
7.如果-2x+3与2x-8的值相等,则x= .
8.已知16a4b和4a2-2nb是同类项,则n2-1= .
0
9.解方程:
(1)40-x-5=20+12x; (2)5y+6-8y=3y-12.
(1)x=
(2)y=3
10.当a为何值时,关于x的方程3x+a=5的解比方程5x-4=6x+8的解大2
解:方程5x-4=6x+8的解为x=-12.
因为-12+2=-10,
所以x=-10是方程3x+a=5的解.
所以3×(-10)+a=5.
解得a=35.
11.整式ax+b的值随x的取值不同而不同,下表是当x取不同值时对应的整式ax+b的值,则关于x的方程-ax-b=6的解是 .
x -2 0 2
ax+b -6 -3 0
x=-2
12.关于x的方程kx-3=2x的解是正整数,则正整数k的可能值有( )
A.1个 B.2个 C.3个 D.4个
B
完成课本对应的习题
谢谢大家观看
年级:七年级上册
数学
第五章 一元一次方程
5.2 解一元一次方程
第二课时 解一元一次方程——移项
学习目标
1. 理解移项的意义,掌握移项的方法.(重点)
2. 学会运用移项解形如“ax+b=cx+d”的一元一
次方程.(重点)
3. 能够抓住实际问题中的数量关系列一元一次方
程解决实际问题.(难点)
1. 解方程:
2. 观察下列一元一次方程,与上题的类型有什么区别?
怎样才能使它向 x=a (a为常数)的形式转化呢?
温故知新
一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
移项的定义
注意:移项一定要变号
移项的依据及注意事项
移项实际上是利用等式的性质1.
易错提醒:
移项是方程中的某一项从方程的一边移到另一边,不要将其与加法的交换律或等式的性质2弄混淆.
解一元一次方程ax+b=cx+d(a,b,c,d均为常数,且a≠c)的一般步骤:
知识要点
ax-cx=d-b
移项
合并同类项
系数化为1
(a-c)x=d-b
移项解一元一次方程
定义
步骤
应用
注意:移项一定要变号
移项
合并同类项
系数化为1
让学习变的简单
PART 01
温故知新
温故知新
课堂导学
核心素养分层练
1.把等式一边的某项 后移到另一边,叫作移项.
2.方程3x=2x+1的解是( )
A.x=-1 B.x=1 C.x= D.x=-
变号
B
知识点:移项
1.若2m-3=3n+1,则2m-3n= .
2.方程3x+7=4x+5的解为x= .
3.若式子5x-7与4x+9的值相等,则x的值是 .
4
2
16
4.若x=-是方程2x-cx=-3+c的解,则c的值为(C)
A.-2 B.- C. D.2
5.王博在做课外习题时遇到如图所示的一道题,其中 是被污损而看不清的一个数,他翻看答案后得知该题的计算结果为15,则 表示的数是( )
A.10 B.-4
C.-10 D.10或-4
A
6.我国古代数学著作《增删算法统宗》记载了“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.”其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,则符合题意的方程是( )
A.2x+5=x+5 B.2x-5=x-5
C.x+5=x+5 D.x+5=x-5
D
1.方程3x=2x+7的解是( )
A.x=4
B.x=-4
C.x=7
D.x=-7
C
2.若x+1的值为6,则x等于( )
A.5 B.-5
C.7 D.-7
3.一元一次方程2x-8=0的解是x= .
4.当x= 时,式子2x-1的值比式子5x+6的值小1.
5.若m+1与-2互为相反数,则m的值为 .
A
4
-2
1
6.下列方程变形中,移项正确的是( )
A.由x+3=6,得x=6+3
B.由2x=x+1,得x-2x=1
C.由-2y=12-y,得y-2y=12
D.由x+5=1-2x,得x-2x=1+5
C
7.如果-2x+3与2x-8的值相等,则x= .
8.已知16a4b和4a2-2nb是同类项,则n2-1= .
0
9.解方程:
(1)40-x-5=20+12x; (2)5y+6-8y=3y-12.
(1)x=
(2)y=3
10.当a为何值时,关于x的方程3x+a=5的解比方程5x-4=6x+8的解大2
解:方程5x-4=6x+8的解为x=-12.
因为-12+2=-10,
所以x=-10是方程3x+a=5的解.
所以3×(-10)+a=5.
解得a=35.
11.整式ax+b的值随x的取值不同而不同,下表是当x取不同值时对应的整式ax+b的值,则关于x的方程-ax-b=6的解是 .
x -2 0 2
ax+b -6 -3 0
x=-2
12.关于x的方程kx-3=2x的解是正整数,则正整数k的可能值有( )
A.1个 B.2个 C.3个 D.4个
B
完成课本对应的习题
谢谢大家观看
同课章节目录
