初中数学人教版九年级上册 22.3 实际问题与二次函数 教学设计(表格式)
文档属性
| 名称 | 初中数学人教版九年级上册 22.3 实际问题与二次函数 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 59.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 00:00:00 | ||
图片预览

文档简介
《实际问题与二次函数》教学设计
学段 年级 九年级 课时名称 实际问题与二次函数一面积问题
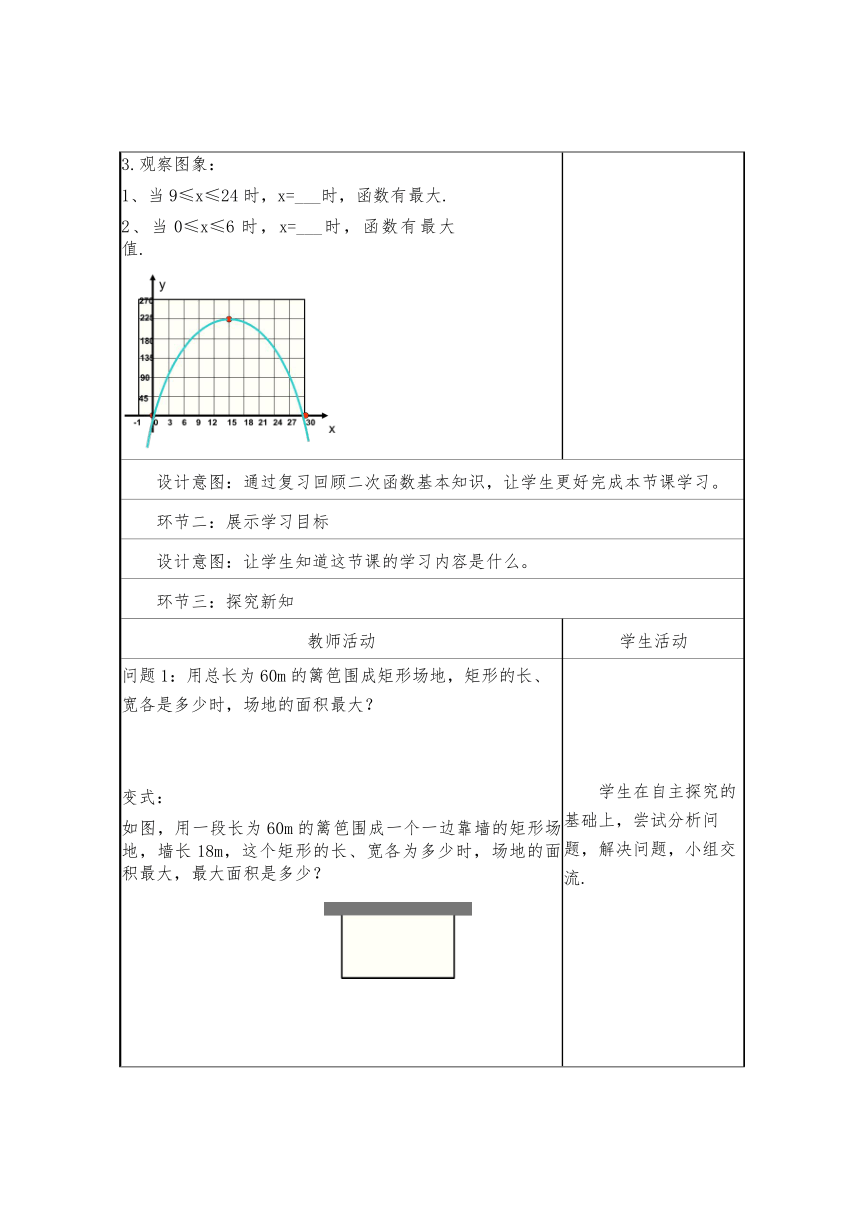
教学内容分析 二次函数是描述现实世界变量之间关系的重要数学模型,运用二次函数可以解决许多实际问题,例如生活中涉及的求最大利润、最大面积等实际问题都与二次函数的最小(大)值有关。本节课是在学生学习二次函数的图象和性质的基础上,借助于二次函数的图象研究二次函数的最小(大)值,并运用这个结论解决相关的实际问题。学情分析 学生已学习二次函数的图象和性质,对求二次函数的最值有了一定的基础,根据实际问题建立二次函数模型对学生来说是难点。学习目标 1.通过小组活动探索现实生活中几何面积问题的函数关系,感受二次函数是刻画现实世界中特定数量关系的一种数学模型. 2.通过经历对实际生活中面积问题的分析过程,能根据问题的已知条件确定二次函数解析式,并运用其性质 解决实际问题,体会数形结合的思想。重难点 1.通过小组活动探索现实生活中几何面积问题的函数关系,感受二次函数是刻画现实世界中特定数量关系的一种数学模型.教学评活动过程环节一:复习回顾教师活动学生活动1. 二次函数y=a(x-h)2+k的图象是一条 ,它的对称轴是 ,顶点坐标是 . 2 .二次函数y=ax2+bx+c的图象是一条 ,它的对称轴是 ,顶点坐标是 . 当a>0时,抛物线开口向 ,有最 点,函数有最 值,是 ;当 a<0时,抛物线开口向 ,有最 点,函数有最 值,是 。 3.观察图象: 1、当9≤x≤24时,x=___时,函数有最大. 2、当0≤x≤6时,x=___时,函数有最大值. 学生回答问题。设计意图:通过复习回顾二次函数基本知识,让学生更好完成本节课学习。环节二:展示学习目标设计意图:让学生知道这节课的学习内容是什么。环节三:探究新知教师活动学生活动问题1:用总长为60m的篱笆围成矩形场地,矩形的长、宽各是多少时,场地的面积最大? 变式: 如图,用一段长为60m的篱笆围成一个一边靠墙的矩形场地,墙长18m,这个矩形的长、宽各为多少时,场地的面积最大,最大面积是多少? 学生在自主探究的基础上,尝试分析问题,解决问题,小组交流.设计意图:问题1是较简单的图形面积最大值问题,学生基本能完成,变式稍有难度,学生通过交流合作,教师引导等将难点解决。通过以上题目的练习,让学生掌握运用二次函数的知识解决实际问题的一般步骤,同时渗透数形结合思想。
环节四:课堂小结
教师活动 学生活动
二次函数解决几何面积最值问题的思路:. 1.设变量(两个) 2.列函数关系式 3.分析自变量的取值范围. 4.求最值 5.答 学生归纳、总结发言,体会,反思。
设计意图:总结回顾学习内容,帮助学生归纳、巩固所学知识。
环节五:达标测试
教师活动 学生活动
1.如图1,用长为24cm的篱笆,一面利用墙(墙长为10m),围成中间隔有一道篱笆的矩形花圃,请求出花圃的最大面积 学生,完成检测。
设计意图:通过测评练习,加深学生对本节知识的理解应用,培养学生良好的分析问题、解决问题的能力和习惯。
板书设计 实际问题与二次函数一面积问题 一般形式:y=ax2+bx+c (k≠0,a,b,c是常数) 顶点坐标: 最值: 变式: 演板:
学段 年级 九年级 课时名称 实际问题与二次函数一面积问题
教学内容分析 二次函数是描述现实世界变量之间关系的重要数学模型,运用二次函数可以解决许多实际问题,例如生活中涉及的求最大利润、最大面积等实际问题都与二次函数的最小(大)值有关。本节课是在学生学习二次函数的图象和性质的基础上,借助于二次函数的图象研究二次函数的最小(大)值,并运用这个结论解决相关的实际问题。学情分析 学生已学习二次函数的图象和性质,对求二次函数的最值有了一定的基础,根据实际问题建立二次函数模型对学生来说是难点。学习目标 1.通过小组活动探索现实生活中几何面积问题的函数关系,感受二次函数是刻画现实世界中特定数量关系的一种数学模型. 2.通过经历对实际生活中面积问题的分析过程,能根据问题的已知条件确定二次函数解析式,并运用其性质 解决实际问题,体会数形结合的思想。重难点 1.通过小组活动探索现实生活中几何面积问题的函数关系,感受二次函数是刻画现实世界中特定数量关系的一种数学模型.教学评活动过程环节一:复习回顾教师活动学生活动1. 二次函数y=a(x-h)2+k的图象是一条 ,它的对称轴是 ,顶点坐标是 . 2 .二次函数y=ax2+bx+c的图象是一条 ,它的对称轴是 ,顶点坐标是 . 当a>0时,抛物线开口向 ,有最 点,函数有最 值,是 ;当 a<0时,抛物线开口向 ,有最 点,函数有最 值,是 。 3.观察图象: 1、当9≤x≤24时,x=___时,函数有最大. 2、当0≤x≤6时,x=___时,函数有最大值. 学生回答问题。设计意图:通过复习回顾二次函数基本知识,让学生更好完成本节课学习。环节二:展示学习目标设计意图:让学生知道这节课的学习内容是什么。环节三:探究新知教师活动学生活动问题1:用总长为60m的篱笆围成矩形场地,矩形的长、宽各是多少时,场地的面积最大? 变式: 如图,用一段长为60m的篱笆围成一个一边靠墙的矩形场地,墙长18m,这个矩形的长、宽各为多少时,场地的面积最大,最大面积是多少? 学生在自主探究的基础上,尝试分析问题,解决问题,小组交流.设计意图:问题1是较简单的图形面积最大值问题,学生基本能完成,变式稍有难度,学生通过交流合作,教师引导等将难点解决。通过以上题目的练习,让学生掌握运用二次函数的知识解决实际问题的一般步骤,同时渗透数形结合思想。
环节四:课堂小结
教师活动 学生活动
二次函数解决几何面积最值问题的思路:. 1.设变量(两个) 2.列函数关系式 3.分析自变量的取值范围. 4.求最值 5.答 学生归纳、总结发言,体会,反思。
设计意图:总结回顾学习内容,帮助学生归纳、巩固所学知识。
环节五:达标测试
教师活动 学生活动
1.如图1,用长为24cm的篱笆,一面利用墙(墙长为10m),围成中间隔有一道篱笆的矩形花圃,请求出花圃的最大面积 学生,完成检测。
设计意图:通过测评练习,加深学生对本节知识的理解应用,培养学生良好的分析问题、解决问题的能力和习惯。
板书设计 实际问题与二次函数一面积问题 一般形式:y=ax2+bx+c (k≠0,a,b,c是常数) 顶点坐标: 最值: 变式: 演板:
同课章节目录
