人教版九年级数学下名师点拨与训练第27章相似第27章 相似 小结与复习
文档属性
| 名称 | 人教版九年级数学下名师点拨与训练第27章相似第27章 相似 小结与复习 |

|
|
| 格式 | doc | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 21:14:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版九年级数学下名师点拨与训练
第27章 相似
第27章 相似 小结与复习
一、知识导图
二、知识清单
知识点一、图形的相似的概念
形状相同的图形叫做相似图形。
1)两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到;
2)全等的图形可以看成是一种特殊的相似,即不仅形状相同,大小也相同;
3)判断两个图形是否相似,就是看两个图形是不是形状相同,与其他因素无关。
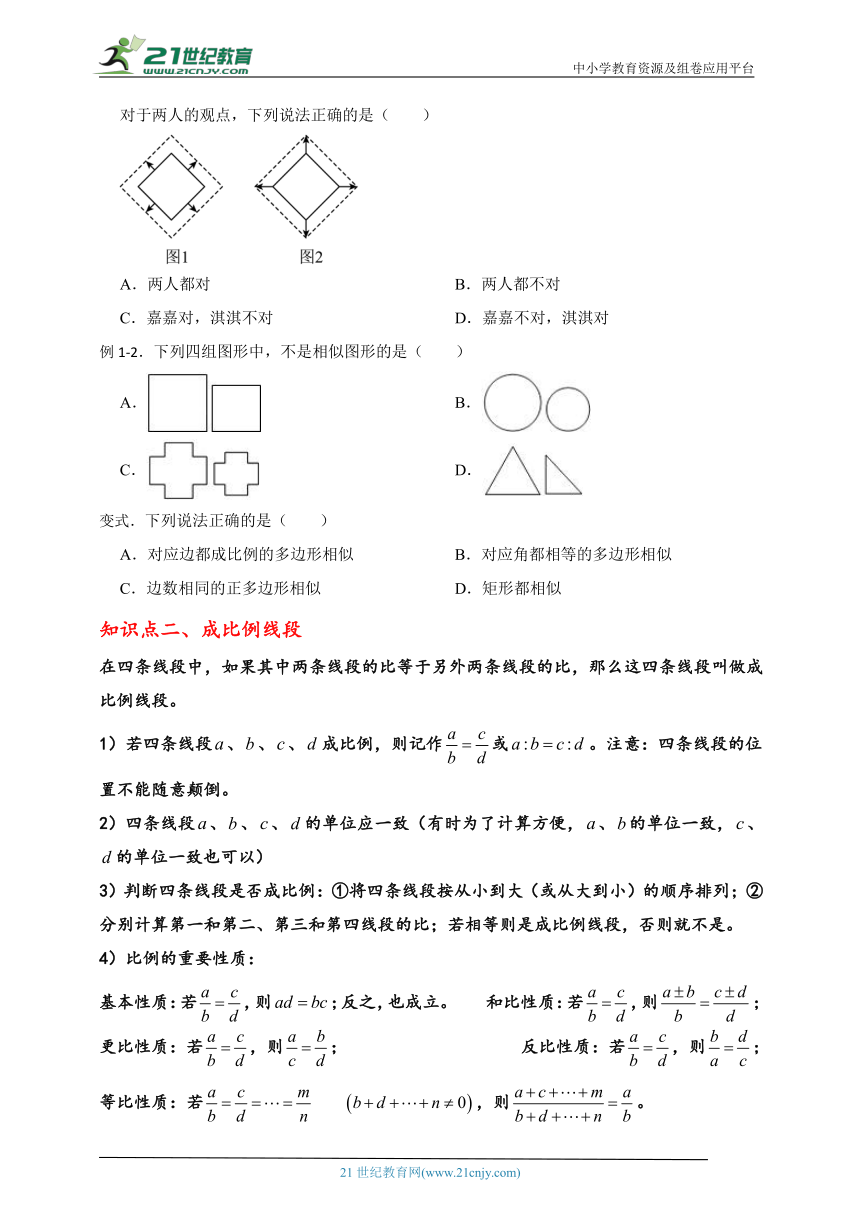
例1-1.在研究相似问题时,嘉嘉和淇淇两同学的观点如下:
嘉嘉:将边长为1的正方形按图1的方式向外扩张,得到新正方形,它们的对应边间距为1,则新正方形与原正方形相似,同时也位似;
淇淇:将边长为1的正方形按图2的方式向外扩张,得到新正方形,每条对角线向其延长线两个方向各延伸1,则新正方形与原正方形相似,同时也位似.
对于两人的观点,下列说法正确的是( )
A.两人都对 B.两人都不对
C.嘉嘉对,淇淇不对 D.嘉嘉不对,淇淇对
例1-2.下列四组图形中,不是相似图形的是( )
A. B.
C. D.
变式.下列说法正确的是( )
A.对应边都成比例的多边形相似 B.对应角都相等的多边形相似
C.边数相同的正多边形相似 D.矩形都相似
知识点二、成比例线段
在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段。
1)若四条线段、、、成比例,则记作或。注意:四条线段的位置不能随意颠倒。
2)四条线段、、、的单位应一致(有时为了计算方便,、的单位一致,、的单位一致也可以)
3)判断四条线段是否成比例:①将四条线段按从小到大(或从大到小)的顺序排列;②分别计算第一和第二、第三和第四线段的比;若相等则是成比例线段,否则就不是。
4)比例的重要性质:
基本性质:若,则;反之,也成立。 和比性质:若,则;
更比性质:若,则; 反比性质:若,则;
等比性质:若,则。
5)拓展:比例式中,或中,、叫外项,、叫内项,、叫前项,、叫后项,如果,那么叫做、的比例中项。
把线段AB分成两条线段AC和BC,使AC2=AB·BC,叫做把线段AB黄金分割,C叫做线段AB的黄金分割点。
例2-1.已知四条线段a,b,c,d是成比例线段,即=,下列说法错误的是( )
A.ad=bc B.= C.= D.=
例2-2.若x是3和6的比例中项,则x的值为( )
A. B. C. D.
变式2-1.有以下命题:
①如果线段d是线段a,b,c的第四比例项,则有 .
②如果点C是线段AB的中点,那么AC是AB、BC的比例中项.
③如果点C是线段AB的黄金分割点,且AC>BC,那么AC是AB与BC的比例中项.
④如果点C是线段AB的黄金分割点,AC>BC,且AB=2,则AC=﹣1.
其中正确的判断有( )
A.1个 B.2个 C.3个 D.4个
变式2-2.已知线段a,b,c满足 ,且a+2b+c=26,则a+2b﹣c= .
知识点三、平行线分线段成比例
平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例。
推论:平行于三角形一边的直线与其他两条直线相交,截得的对应线段成比例。
例3-1.如图,已知直线,直线分别交直线于点,直线分别交直线于点,若,则的值( )
A.大于 B.等于 C.小于 D.不能确定
例3-2.如图,在中,点、为边的三等分点,点、在边上,,交于点.若,则的长为 .
变式3-1. 如图,点D、E是边 上的点,,连接,交点为F,,那么的值是 .
变式3-2.在中,,将绕点B顺时针旋转得到,其中点A,C的对应点分别为点,.当点落在的延长线上时,连接,交于点P,若是方程的两个实数根(),则的面积为 .
知识点四、相似多边形的性质与判定
(1)相似多边形对应角相等,对应边的比相等。
(2)相似比:相似多边形对应边的比称为相似比。
(3)判断两个多边形相似,必须同时具备:(1)边数相同;(2)对应角相等;(3)对应边的比相等。
例4-1.如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E、F.
求证:四边形AFGE与四边形ABCD相似.
例4-2.如图,五边形ABCDE是由五边形FGHMN经过位似变换得到的,点O是位似中心,F、G、H、M、N分别是OA、OB、OC、OD、OE的中点,则五边形ABCDE与五边形FGHMN的面积比是( )
A.2:1 B.4:1 C.5:1 D.6:1
知识点五、相似三角形的相关概念
1)、相似三角形的概念:对应角相等,对应边的比相等的两个三角形是相似三角形。
三角形相似具有传递性。
2)、相似比的概念:相似三角形对应边的比叫做相似比。相似三角形对应边的比是有顺序的。
3、相似三角形与全等三角形的关系:相似三角形不一定是全等三角形,但全等三角形一定是相似三角形。
若两个相似三角形的相似比是1,则这两个三角形是全等三角形,由此可见,全等三角形是相似三角形的一种特例。
例5 .下列说法一定正确的是( )
(A)有两边对应成比例且一角相等的两个三角形相似
(B)对应角相等的两个三角形不一定相似
(C)有两边对应成比例且夹角相等的两个三角形相似
(D)一条直线截三角形两边所得的三角形与原三角形相似
知识点六、相似三角形的判定
判定1:如果两个三角形的三组对应边的比相等,那么这两个三角形相似。
判定2:如果两个三角形的两组对应边的比相等,并且夹角相等,那么这两个三角形相似。
判定3:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
判定4:直角三角形被斜边上的高分成的两个直角三角形与原三角形都相似(此知识常用,用时需要证明)。
例6-1.如图,在四边形中,对角线、相交于点,,且,若,则的值为 .
例6-2.在中,对角线交于点O,E是上一点,且,连结,当时,若则 °,若,则 .
变式6-1.在矩形ABCD中,E为DC边上一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F处.
(1)求证:△ABF∽△FCE;
(2)若AB=8,AD=10,求EC的长.
变式6-2.如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,求FN:ND的值.
知识点七、相似三角形的性质
1、对应角相等,对应边的比相等;
2、拓展:对应高的比,对应中线的比,对应角平分线的比都等于相似比。
3、相似三角形周长的比等于相似比,面积的比等于相似比的平方。(相似多边形周长比等于相似比,相似多边形的面积比等于相似比的平方。)
例7-1.如图,在平行四边形ABCD中,点在对角线BD上,且.
(1)求证:;
(2)若,求AB的长.
例7-2. 如图,中,,,D为边上一点,.
(1)求证:;
(2)如果,求的长.
变式7-1.如图,△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在BC上,AD交PN于点E,BC=48,AD=16.
(1)若PN=18,求DE的长;
(2)若矩形PQMN的周长为80,求矩形PQMN的面积.
知识点八、利用相似三角形测高测距离
1)、利用相似三角形的性质测量河的宽度,计算不能直接测量的物体的高度或深度。
2)、利用三角形的性质来解决实际问题的核心是构造相似三角形,在构造的相似三角形中,被测物体必须是其中一边,注意要把握其余的对应边易测这一原则。
例8-1.如图,某中学两座教学楼中间有个路灯,甲、乙两个人分别在楼上观察路灯顶端,视线所及如图①所示。根据实际情况画出平面图形如图②,CD⊥DF,AB⊥DF,EF⊥DF,甲从点C可以看到点G处,乙从点E恰巧可以看到点D处,点B是DF的中点,路灯AB高5.5米,DF=120米,BG=10.5米,求甲、乙两人的观测点到地面的距离的差。
变式8-1.又到了一年中的春游季节.某班学生利用周末去参观“三军会师纪念塔”.下面是两位同学的一段对话:
甲:我站在此处看塔顶仰角为60°;
乙:我站在此处看塔顶仰角为30°;
甲:我们的身高都是1.6m;
乙:我们相距36m.
请你根据两位同学的对话,计算纪念塔的高度.(精确到1米)
变式8-2.已知如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=2m.
(1)请你画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为4m,请你计算DE的长.
知识点九、位似的概念及性质
1)两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行,象这样的两个图形叫做位似图形,这个点叫做位似中心。这时的相似比又称为位似比。
相似图形与位似图形的区别与联系:1、区别:①位似图形对应点的连线交于一点,相似图形没有;②位似图形的对应边互相平行,相似图形没有。2、联系:位似图形是特殊的相似图形。
2)相似图形与位似图形的区别与联系:
区别:①位似图形对应点的连线交于一点,相似图形没有;
②位似图形的对应边互相平行,相似图形没有。
联系:位似图形是特殊的相似图形。
3)、位似图形是特殊的相似图形,故具有相似图形的一切性质。
4)、位似图形上任意一对对应点到位似中心的距离比等于相似比。
例9-1.如图,DC∥AB,OA=2OC,则△OCD与△OAB的位似比是 .
变式9-1.如图,和是以点为位似中心的位似图形,,则和的面积比值是 .
变式9-2.如图,在平行四边形中,以C为位似中心,作平行四边形的位似平行四边形,且与原图形的位似比为2∶3,连接,若平行四边形的面积为20,则与的面积之和为 .
知识点十、利用位似变换作图(放大或缩小图形)
利用位似变换可以把一个图形放大或缩小,若位似比大于1,则通过位似变换把原图形放大;若位似比小于1,则通过位似变换把原图形缩小。
画位似图形的一般步骤:①确定位似中心;②连线并延长(分别连接位似中心和能代表原图的关键点并延长);③根据相似比确定各线段的长度;④顺次连接上述个点,得到图形。
例10-1.如图,在平面直角坐标系内,顶点坐标分别为,,.
(1)画出关于原点O成中心对称的;
(2)以A为位似中心,在网格中画出,使与位似且面积比为4:1。
变式10-1.如图,在的正方形网格中,每个小正方形的边长均为1,且每个小正方形的顶点称为格点,的顶点均在格点上,按要求完成如下画图.(要求仅用无刻度的直尺,且保留必要的画图痕迹)
(1)在图1中,以为边,画出,使与全等,为格点,请在图1中画出满足条件的所有;
(2)在图2中,以点为位似中心.画出,使与位似,且位似比,点、为格点;
(3)在图3中,在边上找一个点,且满足.
知识点十一、图形的变换与坐标
1)、平移:(1)图形沿x轴平移后,所得新图形的各对应点的纵坐标不变,当向右平移n个单位时,横坐标应相应地加n个单位,反之则减;(2)图形沿y轴平移后,所得新图形的各对应点的横坐标不变,纵坐标上加、下减。
2)、轴对称:(1)图形沿x轴翻折后所得新图形的各对应点的横坐标不变,纵坐标互为相反数;(2)图形沿y轴翻折后所得新图形的各对应点的纵坐标不变,横坐标互为相反数。
3)、以原点为位似中心的位似变换
在平面直角坐标系中,如果位似变化是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k(对应点在位似中心同侧)或者-k(对应点在位似中心异侧)。即:若设原图形的某一点的坐标为,则其位似图形对应点的坐标为或。
例11-1.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
①以O为位似中心在第二象限作位似比为1:2变换,得到对应的△A1B1C1,画出△A1B1C1,并写出C1的坐标;
②以原点O为旋转中心,画出把△ABC顺时针旋转90°的图形△A2B2C2,并写出C2的坐标.
变式11-1.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,
(2)点C1的坐标是 ;
(3)以点B为位似中心,在网格内画出△A2B2C2,
(4)使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
三、核心素养提升
数学建模-构建相似三角形模型解决实际问题
1.在《数书九章》(宋·秦九韶)中记载了一个测量塔高的问题:如图所示,表示塔的高度,表示竹竿顶端到地面的高度,表示人眼到地面的高度,、、在同一平面内,点A、C、E在一条水平直线上.已知米,米,米,米,人从点F远眺塔顶B,视线恰好经过竹竿的顶端D,可求出塔的高度.根据以上信息,塔的高度为 米.
2.如图,小李利用镜面反射原理测树高,小李在点,镜子为点,表示树,点,,在同一水平线上,小李身高米,米,米,则树高为( )
A.4米 B.5米 C.6米 D.7米
3.小亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD处,另一部分在某一建筑的墙上CD处,分别测得其长度为9.6米和2米,求旗杆AB的高度.
2.逻辑推理-利用相似三角形的判定和性质进行推理
4.如图,点E在菱形ABCD的边BC的延长线上,AE交CD于点F,FG∥CE交DE于点G.求证:FG=FC.
5.如图,AC是⊙O的直径,弦BD交AC于点E.
(1)求证:△ADE∽△BCE;
(2)如果AD2=AE·AC,求证:CD=CB.
6.已知AD⊥BC,BE=CE,∠ABC=2∠C,BF为∠B的平分线.求证:AB=2DE.
【答案】解:连接EF.
3.分类讨论思想
7.如图,BA⊥MN,垂足为A,BA=4,点P是射线AN上的一个动点(点P与点A不重合),且∠BPC=∠BPA,BC⊥BP,过点C作CD⊥MN,垂足为D,设AP=x
(1)CD的长度是否随着的x变化而变化?若变化,请用含的x代数式表示CD的长度;若不变化,请求出线段CD的长度;
(2)当x取何值时,△ABP和△CDP相似.
8.在△ABC中,D,E分别是AC,AB边上的点,AD=3,AE=2,AC=5,当AB= 时,△ADE与△ABC相似.
9.已知Rt△ABC中,∠C=90°,∠A≠∠B,点P是边AC上一点(不与A、C重合),过P点的一条直线与△ABC的边相交,所构成的三角形与原三角形相似,这样的直线有( )条.
A.1 B.2 C.3 D.4
10.如图,在四边形,,,,,.动点从点出发,沿折线以每秒3个单位长度的速度向终点运动.当点不与点A、B、重合时,作点关于直线PD的对称点,连接、,设点的运动时间为秒.
(1)线段CD的长为 ;
(2)当为直角三角形时,求的值;
(3)作点关于直线PD的对称点,连接.
①当时,求的值;
②连接,当直线经过点A时,直接写出的值.
4.方程的思想
11.
(1)如图1,在矩形中,,,点E为边上一点,沿直线将矩形折叠,使点C落在边上的点处.求的长;
(2)如图2,展开后,将沿线段向右平移,使点的对应点与点B重合,得到,与交于点F,求线段的长;
(3)在图1中,将绕点旋转至A,,E三点共线时,请直接写出的长.
12.如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交射线BC于点E,设AP=x.
⑴当x为何值时,△APD是等腰三角形
⑵若设BE=y,求y关于x的函数关系式;
⑶若BC的长可以变化,在现在的条件下,是否存在点P,使得PQ经过点C 若存在,求出相应的AP的长;若不存在,请说明理由,并直接写出当BC的长在什么范围内时,可以存在这样的点P,使得PQ经过点C.
人教版九年级数学下名师点拨与训练
第27章 相似
第27章 相似 小结与复习
一、知识导图
二、知识清单
知识点一、图形的相似的概念
形状相同的图形叫做相似图形。
1)两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到;
2)全等的图形可以看成是一种特殊的相似,即不仅形状相同,大小也相同;
3)判断两个图形是否相似,就是看两个图形是不是形状相同,与其他因素无关。
例1-1.在研究相似问题时,嘉嘉和淇淇两同学的观点如下:
嘉嘉:将边长为1的正方形按图1的方式向外扩张,得到新正方形,它们的对应边间距为1,则新正方形与原正方形相似,同时也位似;
淇淇:将边长为1的正方形按图2的方式向外扩张,得到新正方形,每条对角线向其延长线两个方向各延伸1,则新正方形与原正方形相似,同时也位似.
对于两人的观点,下列说法正确的是( )
A.两人都对 B.两人都不对
C.嘉嘉对,淇淇不对 D.嘉嘉不对,淇淇对
【答案】A
【知识点】图形的相似;位似图形的概念
例1-2.下列四组图形中,不是相似图形的是( )
A. B.
C. D.
【答案】D
【知识点】图形的相似
【解析】【解答】解:A、形状相同,但大小不同,符合相似形的定义,故不符合题意;
B、形状相同,但大小不同,符合相似形的定义,故不符合题意;
C、形状相同,但大小不同,符合相似形的定义,故不符合题意;
D、形状不相同,不符合相似形的定义,故符合题意;
故选:D.
【分析】根据相似图形的定义,对选项进行一一分析,排除错误答案.
变式.下列说法正确的是( )
A.对应边都成比例的多边形相似 B.对应角都相等的多边形相似
C.边数相同的正多边形相似 D.矩形都相似
【答案】C
【知识点】图形的相似
【解析】【分析】根据相似图形的定义,对选项一一分析,排除错误答案。
【解答】A、对应边都成比例的多边形,属于形状不唯一确定的图形,故错误;
B、对应角都相等的多边形,属于形状不唯一确定的图形,故错误;
C、边数相同的正多边形,形状相同,大小不一定相同,故正确;
D、矩形属于形状不唯一确定的图形,故错误。
故选C.
【点评】本题考查相似变换的定义,即图形的形状相同,但大小不一定相同的是相似形。
知识点二、成比例线段
在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段。
1)若四条线段、、、成比例,则记作或。注意:四条线段的位置不能随意颠倒。
2)四条线段、、、的单位应一致(有时为了计算方便,、的单位一致,、的单位一致也可以)
3)判断四条线段是否成比例:①将四条线段按从小到大(或从大到小)的顺序排列;②分别计算第一和第二、第三和第四线段的比;若相等则是成比例线段,否则就不是。
4)比例的重要性质:
基本性质:若,则;反之,也成立。 和比性质:若,则;
更比性质:若,则; 反比性质:若,则;
等比性质:若,则。
5)拓展:比例式中,或中,、叫外项,、叫内项,、叫前项,、叫后项,如果,那么叫做、的比例中项。
把线段AB分成两条线段AC和BC,使AC2=AB·BC,叫做把线段AB黄金分割,C叫做线段AB的黄金分割点。
例2-1.已知四条线段a,b,c,d是成比例线段,即=,下列说法错误的是( )
A.ad=bc B.= C.= D.=
【答案】C
【知识点】比例线段
【解析】【分析】根据比例的性质将原式变形,分别进行判断即可,进而得出答案.
【解答】∵四条线段a,b,c,d是成比例线段,即=,
∴A.利用内项之积等于外项之积,ad=bc,故选项正确,
B.利用内项之积等于外项之积,a(b+d)=b(a+c),ab+ad=ab+bc,即ad=bc,故选项正确,
C.∵=,
∴=,故选项错误,
D.∵=∴=,故选项正确.
故选:C.
【点评】此题主要考查了比例的性质,将比例式灵活正确变形得出是解题关键.
例2-2.若x是3和6的比例中项,则x的值为( )
A. B. C. D.
【答案】D
【知识点】比例线段
【解析】【分析】根据比例中项的概念,得x2=3×6,则x可求出来.
【解答】∵x是3和6的比例中项,
∴x2=3×6=18,
解得x=.
故选D.
【点评】本题考查了比例中项的概念:当比例式中的两个内项相同时,即叫比例中项.求比例中项根据比例的基本性质进行计算.
变式2-1.有以下命题:
①如果线段d是线段a,b,c的第四比例项,则有 .
②如果点C是线段AB的中点,那么AC是AB、BC的比例中项.
③如果点C是线段AB的黄金分割点,且AC>BC,那么AC是AB与BC的比例中项.
④如果点C是线段AB的黄金分割点,AC>BC,且AB=2,则AC=﹣1.
其中正确的判断有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【知识点】比例线段;黄金分割
【解析】【解答】解:①、根据第四比例项的概念,显然正确;
②、如果点C是线段AB的中点,AB:AC=2,AC:BC=1,不成比例,错误;
③、根据黄金分割的概念,正确;
④、根据黄金分割的概念:AC= ﹣1,错误.
故选B.
【分析】根据比例中项和黄金分割的概念分析各个说法.
变式2-2.已知线段a,b,c满足 ,且a+2b+c=26,则a+2b﹣c= .
【答案】2
【知识点】比例线段
【解析】【解答】解:设 =k,则有a=3k,b=2k,c=6k,
代入已知等式得:3k+4k+6k=26,
解得:k=2,即a=6,b=4,c=12,
则原式=6+8﹣12=2,
故答案为:2
【分析】设已知比例式值为k,表示出a,b,c,代入已知等式求出k的值,确定出a,b,c的值,代入原式计算即可得到结果.
知识点三、平行线分线段成比例
平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例。
推论:平行于三角形一边的直线与其他两条直线相交,截得的对应线段成比例。
例3-1.如图,已知直线,直线分别交直线于点,直线分别交直线于点,若,则的值( )
A.大于 B.等于 C.小于 D.不能确定
【答案】A
【知识点】平行四边形的判定与性质;两条直线被一组平行线所截,所得的对应线段成比例
【解析】【解答】解:作分别交、于、,
∵,
∴四边形、四边形是平行四边形,
,
,
,即,
故答案为:A.
【分析】作分别交、于、,可得四边形、四边形是平行四边形,,然后根据平行线分线段成比例求出,再进一步计算的值即可.
例3-2.如图,在中,点、为边的三等分点,点、在边上,,交于点.若,则的长为 .
【答案】
【知识点】平行线的判定与性质;两条直线被一组平行线所截,所得的对应线段成比例;相似三角形的判定与性质
【解析】【解答】点,为边的三等分点,
∴BE=ED=AD,
,
,
,
,
,
点,为边的三等分点,,
点,为边的三等分点,
,
,
,
.
故答案为:。
【分析】先证出,再利用相似三角形的性质求得的长度,利用平行线分线段成比例定理求得,最后利用相似三角形的判定与性质解答即可得出结论.
变式3-1. 如图,点D、E是边 上的点,,连接,交点为F,,那么的值是 .
【答案】
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
【解析】【解答】解:过作,交于,如图所示:
则,即:,,
,即:,
∴.
故答案为:
【分析】过作,交于,进而根据平行线分线段成比例结合题意即可求解。
变式3-2.在中,,将绕点B顺时针旋转得到,其中点A,C的对应点分别为点,.当点落在的延长线上时,连接,交于点P,若是方程的两个实数根(),则的面积为 .
【答案】
【知识点】因式分解法解一元二次方程;两条直线被一组平行线所截,所得的对应线段成比例;旋转的性质
【解析】【解答】解:作交于,过作于,
∵是方程的两个实数根(),
∴,,
∴,
∵将绕点B顺时针旋转得到,
∴,,,,
∵
∴,
∴,
∵
∴,
∴,
∴,
∴,
∴,
∵
∴,
∴,解得,
∴,
∴,
∴,
故答案为:.
【分析】 先解方程可得AC=4,BC=3,再作CM∥BP交AB于点M,过C作CD⊥AB于点D,即可求出CD、BD的长度,再由旋转的性质和平行线的性质可得∠CBA=∠CMB,即可得到CM=BC,MD=BD,再由平行线分线段成比例求出BP,最后根据求解即可.
知识点四、相似多边形的性质与判定
(1)相似多边形对应角相等,对应边的比相等。
(2)相似比:相似多边形对应边的比称为相似比。
(3)判断两个多边形相似,必须同时具备:(1)边数相同;(2)对应角相等;(3)对应边的比相等。
例4-1.如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E、F.
求证:四边形AFGE与四边形ABCD相似.
【答案】证明:∵四边形ABCD是正方形,AC是对角线,
∴∠DAC=∠BAC=45°.
又∵GE⊥AD,GF⊥AB,
∴EG=FG,且AE=EG,AF=FG.
∴AE=EG=FG=AF,
即四边形AFGE为正方形.
∴ = = = ,且∠EAF=∠DAB,∠AFG=∠ABC,∠FGE=∠BCD,∠AEG=∠ADC.
∴四边形AFGE与四边形ABCD相似
【知识点】相似多边形
【解析】【分析】由正方形的性质可知;AC平分∠DAB,然后由角平分线的性质可知GE=GF,从而可证明四边形EGFA为正方形,故此四边形AFGE与四边形ABCD相似.本题主要考查的是相似多边形的判定、正方形的判定、角平分线的性质,证得四边形EAFG为正方形是解题的关键.
例4-2.如图,五边形ABCDE是由五边形FGHMN经过位似变换得到的,点O是位似中心,F、G、H、M、N分别是OA、OB、OC、OD、OE的中点,则五边形ABCDE与五边形FGHMN的面积比是( )
A.2:1 B.4:1 C.5:1 D.6:1
【答案】B
【知识点】相似多边形;位似变换
【解析】【解答】解:∵F为AO的中点,
∴OF:OA=1:2,
∵ 五边形ABCDE是由五边形FGHMN经过位似变换得到的 ,
∴FN∥AE,
∴△OFN∽△OAE,
∴OF∶OA=FN∶AE=1∶2
∴五边形ABCDE与五边形FGHMN的面积比为:4:1.
故答案为:B.
【分析】由五边形ABCDE与五边形FGHMN关于点O成位似关系,且OF:OA=1:2,可得位似比为1:2,根据形似图形的面积比等于相似比的平方,即可求得答案.
知识点五、相似三角形的相关概念
1)、相似三角形的概念:对应角相等,对应边的比相等的两个三角形是相似三角形。
三角形相似具有传递性。
2)、相似比的概念:相似三角形对应边的比叫做相似比。相似三角形对应边的比是有顺序的。
3、相似三角形与全等三角形的关系:相似三角形不一定是全等三角形,但全等三角形一定是相似三角形。
若两个相似三角形的相似比是1,则这两个三角形是全等三角形,由此可见,全等三角形是相似三角形的一种特例。
例5 .下列说法一定正确的是( )
(A)有两边对应成比例且一角相等的两个三角形相似
(B)对应角相等的两个三角形不一定相似
(C)有两边对应成比例且夹角相等的两个三角形相似
(D)一条直线截三角形两边所得的三角形与原三角形相似
【答案】C
【解析】根据判定定理2可知A错误,C正确;根据判定定理1可知B错误,根据相似三 角形预备定理可知只有直线与底边平行时才相似.
【总结】考查相似三角形的判定定理掌握情况和相关条件.
知识点六、相似三角形的判定
判定1:如果两个三角形的三组对应边的比相等,那么这两个三角形相似。
判定2:如果两个三角形的两组对应边的比相等,并且夹角相等,那么这两个三角形相似。
判定3:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
判定4:直角三角形被斜边上的高分成的两个直角三角形与原三角形都相似(此知识常用,用时需要证明)。
例6-1.如图,在四边形中,对角线、相交于点,,且,若,则的值为 .
【答案】
【知识点】相似三角形的判定;解直角三角形—边角关系
【解析】【解答】解:如图:
过点D作DE⊥BC于点E.
∴,
设DE=3x,DB=5x,则BE=4x.
∵DC=DB=5x,
∴CE=BE=4x,BC=8x.
过点A作AG//BC交DB于点G,
∴,∠AHD=∠CEH=90°=∠AHE.
∵,
∴∠GAD=∠GAB=∠ABC.
∴△DAH∽△ABC.
∴.
∵,
∴四边形ACEH是矩形,
∴.
∴
故答案为:.
【分析】过点D作DE⊥BC于点E.根据 ,设DE=3x,结合DC=DB可表示出BE,CE,BD.过点A作AG//BC交DB于点G,根据可证得∠GAD=∠GAB=∠ABC以及∠AHD=∠CEH=90°=∠AHE.可得△DAH∽△ABC和四边形ACEH是矩形,于是可得,可得结果.
例6-2.在中,对角线交于点O,E是上一点,且,连结,当时,若则 °,若,则 .
【答案】;
【知识点】相似三角形的性质;相似三角形的判定;四边形的综合
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AB//CD,∠BCD=∠BAD.
∵
∴,
∴∠AED=∠BAE=90°,
①∵,,AD=DA,
∴△OAD≌△EDA(SAS)
∴∠AOD=∠AED=90°,∠ODA=∠EAD.
∴AC⊥BD,
∴ 是菱形.
∴AB=BC=CD=AD.
∴∠ODC=∠ODA=∠EAD.
∵在直角三角形AED中,∠EAD+∠ODA+∠ODC=3∠EAD=90°.
∴∠ABC=∠ADC=60°.
②在DE上选取点F,使EF=CE,连接AF. 如图所示:
∵AE⊥CF,
∴AC=AF,
∴∠CAE=∠FAE,∠ACE=∠AFE.
∴.
∵∠OCD=∠FCA,
∴△OCD∽△FCA.
∴
∵AO=CO=DE,
∴
令,
∴.
解得:(舍负)
故
故答案为:60°;.
【分析】先根据平行四边形的性质以及角的换算,得出∠AED=90°,再证明△OAD≌△EDA ( SAS) ,得∠AOD=∠AED=90°,∠ODA=∠EAD.于是可得四边形ABCD为菱形,根据菱形的对角线平分对角和直角三角形两锐角互余,得3∠EAD=90°,可求∠ABC的度数;
在DE上选取点F,使EF=CE,连接AF.根据线段垂直平分线的性质得AC=AF,于是可证明△OCD∽△FCA,得,结合AO=CO=DE,可得,令,得到关于x的方程,求解即可.
变式6-1.在矩形ABCD中,E为DC边上一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F处.
(1)求证:△ABF∽△FCE;
(2)若AB=8,AD=10,求EC的长.
【答案】(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,
∴∠BAF+∠AFB=90°,
由翻折可得:
∠D=∠AFE=90°,
∴∠AFB+∠EFC=90°,
∴∠BAF=∠EFC,
∵∠B=∠C,
∴△ABF∽△FCE;
(2)解:∵四边形ABCD是矩形,AD=10,
∴BC=10,
由翻折可得:
AF=10,
在Rt△ABF中,
,
∴CF=10﹣6=4,
∵△ABF∽△FCE,
∴,
∴,
∴CE=3.
【知识点】矩形的性质;翻折变换(折叠问题);相似三角形的判定
【解析】【分析】(1)根据四边形ABCD是矩形,得出∠B=∠C=∠D=90°,由翻折可得:∠D=∠AFE=90°,利用同角的余角相等可以得出∠BAF=∠EFC,即可证出结论;
(2)由翻折可得:AF=10,根据勾股定理得出BF=6,利用 △ABF∽△FCE ,求解即可EC.
变式6-2.如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,求FN:ND的值.
【答案】解:过点F作FE∥BD,交AC于点E,∴,∵AF:BF=1:2,∴=,∴,即FE=BC,∵BC:CD=2:1,∴CD=BC,∵FE∥BD,∴.即FN:ND=2:3.
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
【解析】【分析】过点F作FE∥BD,交AC于点E,求出,得出FE=BC,根据已知推出CD=BC,根据平行线分线段成比例定理推出=,代入化简即可.本题考查了平行线分线段成比例定理的应用,注意:平行线分的线段对应成比例,此题具有一定的代表性,但是一定比较容易出错的题目.
知识点七、相似三角形的性质
1、对应角相等,对应边的比相等;
2、拓展:对应高的比,对应中线的比,对应角平分线的比都等于相似比。
3、相似三角形周长的比等于相似比,面积的比等于相似比的平方。(相似多边形周长比等于相似比,相似多边形的面积比等于相似比的平方。)
例7-1.如图,在平行四边形ABCD中,点在对角线BD上,且.
(1)求证:;
(2)若,求AB的长.
【答案】(1)证明:∵四边形ABCD为平行四边形,
,
(2)解:
.
【知识点】平行四边形的性质;相似三角形的判定与性质
【解析】【分析】(1)根据平行四边形的性质,推出从而证明;
(2)根据相似三角形对应边成比例,列出比例式,即可求出AB长.
例7-2. 如图,中,,,D为边上一点,.
(1)求证:;
(2)如果,求的长.
【答案】(1)证明:∵,,
∴,
∵,
∴
(2)解:∵,
∴
∴,
∵,
∴.
【知识点】相似三角形的判定与性质
【解析】【分析】(1)根据相似三角形的判定,对应边成比例且夹角相等证出即可.
(2)根据相似三角形对应边成比例求解即可.
变式7-1.如图,△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在BC上,AD交PN于点E,BC=48,AD=16.
(1)若PN=18,求DE的长;
(2)若矩形PQMN的周长为80,求矩形PQMN的面积.
【答案】(1)解:依题意得:PN∥BC,则△APN∽△ABC,
又AD是高,则,
设DE=,则AE=16-,
由得,,解之得,=10
(2)解:由矩形PQMN,又AD是高,则四边形PQDE为矩形,
∴DE=PQ,
设DE=PQ=,则PN=,
同理得,
解得=4
则矩形PQMN的面积=
【知识点】矩形的判定与性质;相似三角形的判定与性质
【解析】【分析】(1)先根据相似三角形的判定与性质证明△APN∽△ABC得到,设DE=,则AE=16-,进而代入即可求解;
(2)先根据矩形的判定与性质得到DE=PQ,设DE=PQ=,则PN=,进而求出y,再根据矩形的面积公式即可求解。
知识点八、利用相似三角形测高测距离
1)、利用相似三角形的性质测量河的宽度,计算不能直接测量的物体的高度或深度。
2)、利用三角形的性质来解决实际问题的核心是构造相似三角形,在构造的相似三角形中,被测物体必须是其中一边,注意要把握其余的对应边易测这一原则。
例8-1.如图,某中学两座教学楼中间有个路灯,甲、乙两个人分别在楼上观察路灯顶端,视线所及如图①所示。根据实际情况画出平面图形如图②,CD⊥DF,AB⊥DF,EF⊥DF,甲从点C可以看到点G处,乙从点E恰巧可以看到点D处,点B是DF的中点,路灯AB高5.5米,DF=120米,BG=10.5米,求甲、乙两人的观测点到地面的距离的差。
【答案】解:∵AB⊥DF,EF⊥DF,
∴∠ABD=∠F=90°,
又∵∠EDF=∠ADB,
∴△DAB~△DEF,
同理得△GAB~△GCD,
∵点B是DF的中点,
∴DB=BF= DF= ×120=60,
∵
∴EF=2AB=2x5.5=11,
∵BG=10.5,
∴DG=10.5+60=70.5
∴CD= AB= ×55≈36.9
∴甲、乙两人的观察点到地面的距离的差为:36.9-11=25.9(米)
【知识点】相似三角形的应用
【解析】【分析】利用垂直的定义可证∠ABD=∠F,再利用有两组对应角相等的两三角形相似,可证得△DAB~△DEF,同理得△GAB~△GCD,再利用相似三角形的对应边成比例,就可求出EF,DG的长,然后求出CD的长即甲、乙两人的观测点到地面的距离的差。
变式8-1.又到了一年中的春游季节.某班学生利用周末去参观“三军会师纪念塔”.下面是两位同学的一段对话:
甲:我站在此处看塔顶仰角为60°;
乙:我站在此处看塔顶仰角为30°;
甲:我们的身高都是1.6m;
乙:我们相距36m.
请你根据两位同学的对话,计算纪念塔的高度.(精确到1米)
【答案】解:如图,CD=EF=BH=1.6m,CE=DF=36m,∠ADH=30°,∠AFH=30°,
在Rt△AHF中,∵tan∠AFH=,
∴FH=,
在Rt△ADH中,∵tan∠ADH=,
∴DH=,
而DH﹣FH=DF,
∴﹣=36,即﹣=36,
∴AH=18,
∴AB=AH+BH=18+1.6≈33(m).
答:纪念塔的高度约为33m.
【知识点】相似三角形的应用
【解析】【分析】先画出几何图形,如图,CD=EF=BH=1.6m,CE=DF=36m,∠ADH=30°,∠AFH=30°,分别利用正切定义得到FH=,DH=,则﹣=36,再利用特殊角的函数值可计算出AH=18,然后计算AH+BH即可.
变式8-2.已知如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=2m.
(1)请你画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为4m,请你计算DE的长.
【答案】解:(1)如图,EF为此时DE在阳光下的投影;
(2)∵AC∥DF,
∴∠ACB=∠DFE,
∴Rt△ABC∽Rt△DEF,
∴,即,解得DE=10(m),
即DE的长为10m.
【知识点】相似三角形的应用;平行投影
【解析】【分析】(1)连结AC,过点D作DF∥AC,则EF为所求;
(2)先证明Rt△ABC∽Rt△DEF,然后利用相似比计算出DE的长.
知识点九、位似的概念及性质
1)两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行,象这样的两个图形叫做位似图形,这个点叫做位似中心。这时的相似比又称为位似比。
相似图形与位似图形的区别与联系:1、区别:①位似图形对应点的连线交于一点,相似图形没有;②位似图形的对应边互相平行,相似图形没有。2、联系:位似图形是特殊的相似图形。
2)相似图形与位似图形的区别与联系:
区别:①位似图形对应点的连线交于一点,相似图形没有;
②位似图形的对应边互相平行,相似图形没有。
联系:位似图形是特殊的相似图形。
3)、位似图形是特殊的相似图形,故具有相似图形的一切性质。
4)、位似图形上任意一对对应点到位似中心的距离比等于相似比。
例9-1.如图,DC∥AB,OA=2OC,则△OCD与△OAB的位似比是 .
【答案】1:2
【知识点】位似变换
【解析】解:∵DC∥AB
∴△OAB∽△OCD
∵△OCD与OAB的对应点的连线都过点O
∴△OCD与△OAB的位似
∴△OCD与△OAB的位似比为OC:OA=1:2.
【分析】先证明△OAB∽△OCD,△OCD与OAB的对应点的连线都过点O,所以可得△OCD与△OAB的位似,即可求得△OCD与△OAB的位似比为OC:OA=1:2.
变式9-1.如图,和是以点为位似中心的位似图形,,则和的面积比值是 .
【答案】
【知识点】相似三角形的性质;位似变换
【解析】【解答】解:∵△ABC和△DEF是以点O为位似中心的位似图形,
∴△ABC∽△DEF,
∵OA:OD=2:3,
∴AB:DE=2:3,
∴.
故答案为:.
【分析】根据位似的性质得△ABC∽△DEF,由已知OA:OD=2:3,得AB:DE=2:3,根据相似三角形的性质得,即可求解.
变式9-2.如图,在平行四边形中,以C为位似中心,作平行四边形的位似平行四边形,且与原图形的位似比为2∶3,连接,若平行四边形的面积为20,则与的面积之和为 .
【答案】10
【知识点】平行四边形的性质;位似变换
【解析】【解答】解:连接,如图所示:
∵平行四边形和平行四边形是位似图形,且位似比为2∶3,
∴,,
∴,,
∴,,
∴,
∴,
故答案为:10
【分析】连接,先根据位似结合题意得到,,进而得到,,再根据“”即可求解。
知识点十、利用位似变换作图(放大或缩小图形)
利用位似变换可以把一个图形放大或缩小,若位似比大于1,则通过位似变换把原图形放大;若位似比小于1,则通过位似变换把原图形缩小。
画位似图形的一般步骤:①确定位似中心;②连线并延长(分别连接位似中心和能代表原图的关键点并延长);③根据相似比确定各线段的长度;④顺次连接上述个点,得到图形。
例10-1.如图,在平面直角坐标系内,顶点坐标分别为,,.
(1)画出关于原点O成中心对称的;
(2)以A为位似中心,在网格中画出,使与位似且面积比为4:1。
【答案】(1)解:如图,即为所求作的三角形;
(2)解:如图,与即为所求作的三角形.
【知识点】作图﹣位似变换;作图﹣旋转
【解析】【分析】(1)根据对称性质作出A、B、C关于原点的对称点A1、B1、C1,顺次连接即可;
(2)根据位似图形的性质得出对应点位置,再顺次连接即可求解.
变式10-1.如图,在的正方形网格中,每个小正方形的边长均为1,且每个小正方形的顶点称为格点,的顶点均在格点上,按要求完成如下画图.(要求仅用无刻度的直尺,且保留必要的画图痕迹)
(1)在图1中,以为边,画出,使与全等,为格点,请在图1中画出满足条件的所有;
(2)在图2中,以点为位似中心.画出,使与位似,且位似比,点、为格点;
(3)在图3中,在边上找一个点,且满足.
【答案】(1)解:如图,和和即为所作,
;
(2)解:如图,即为所作,
;
(3)解:如图所示,取格点,,连接,交于点,则点即为所求作的点.
【知识点】作图﹣位似变换;尺规作图-作三角形
【解析】【分析】
(1)根据全等三角形的性质即可作出;
(2)根据位似图形的性质以及相似三角形的性质即可画出△EFC;
(3)取格点E,F,连接EF,交AC于P点,则点P即为所求作的点,由图可得△APF∽△CPE,从而得出.
知识点十一、图形的变换与坐标
1)、平移:(1)图形沿x轴平移后,所得新图形的各对应点的纵坐标不变,当向右平移n个单位时,横坐标应相应地加n个单位,反之则减;(2)图形沿y轴平移后,所得新图形的各对应点的横坐标不变,纵坐标上加、下减。
2)、轴对称:(1)图形沿x轴翻折后所得新图形的各对应点的横坐标不变,纵坐标互为相反数;(2)图形沿y轴翻折后所得新图形的各对应点的纵坐标不变,横坐标互为相反数。
3)、以原点为位似中心的位似变换
在平面直角坐标系中,如果位似变化是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k(对应点在位似中心同侧)或者-k(对应点在位似中心异侧)。即:若设原图形的某一点的坐标为,则其位似图形对应点的坐标为或。
例11-1.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
①以O为位似中心在第二象限作位似比为1:2变换,得到对应的△A1B1C1,画出△A1B1C1,并写出C1的坐标;
②以原点O为旋转中心,画出把△ABC顺时针旋转90°的图形△A2B2C2,并写出C2的坐标.
【答案】解:①如图所示:△A1B1C1,即为所求,
C1的坐标为:(﹣8,2);
②如图所示:△A2B2C2,即为所求,
C2的坐标为:(﹣1,﹣4).
【知识点】作图﹣位似变换
【解析】【分析】①直接利用位似图形的性质得出对应点位置进而得出答案;②直接利用旋转的性质得出对应点位置,进而得出答案.
变式11-1.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,
(2)点C1的坐标是 ;
(3)以点B为位似中心,在网格内画出△A2B2C2,
(4)使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
【答案】(1)如图△A1B1C1
(2)(2,﹣2)
(3)如图△A2B2C2
(4)(1,0)
【知识点】作图﹣位似变换
【解析】【解答】解:(1.)如图所示,画出△ABC向下平移4个单位长度得到的△A1B1C1,
(2.)点C1的坐标是(2,﹣2);
(3.)如图所示,以B为位似中心,画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,
(4.)点C2的坐标是(1,0),
【分析】(1)将△ABC向下平移4个单位长度得到的△A1B1C1,如图所示,(2)找出所求点坐标即可;(3)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,如图所示,(4)找出所求点坐标即可.
三、核心素养提升
数学建模-构建相似三角形模型解决实际问题
1.在《数书九章》(宋·秦九韶)中记载了一个测量塔高的问题:如图所示,表示塔的高度,表示竹竿顶端到地面的高度,表示人眼到地面的高度,、、在同一平面内,点A、C、E在一条水平直线上.已知米,米,米,米,人从点F远眺塔顶B,视线恰好经过竹竿的顶端D,可求出塔的高度.根据以上信息,塔的高度为 米.
【答案】
【知识点】相似三角形的应用
【解析】【解答】解:如图,过作于,交于,
则,,,,
∴,
∵,
∴,
∴,
∴,解得:,
∴(米),
故答案为:.
【分析】本题根据相似三角形的预备定理:得出,再根据相似三角形的性质:对应边成比例,列出比例式:,求出QB,再通过计算出AB即可.
2.如图,小李利用镜面反射原理测树高,小李在点,镜子为点,表示树,点,,在同一水平线上,小李身高米,米,米,则树高为( )
A.4米 B.5米 C.6米 D.7米
【答案】A
【知识点】相似三角形的应用;一线三等角相似模型(K字型相似模型)
【解析】【解答】解:根据题意可知: ∠CAO=∠DBO=90°,∠COF=∠DOF,
故∠COA+∠COF=90°,∠DOB+∠DOF=90°,
∴∠COA=∠DOB,
∴△ACO∽△BDO,
∴,
∵AC=1.6米,OA=2.4米,OB=6米,
∴,
解得: BD=4,
即树高为4米.
故答案为:A.
【分析】根据等角的余角相等得出∠COA=∠DOB,根据有两个角相等的两个三角形是相似三角形得出△ACO∽△BDO,根据相似三角形的对应边之比相等,即可代入数据,求出BD的值.
3.小亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD处,另一部分在某一建筑的墙上CD处,分别测得其长度为9.6米和2米,求旗杆AB的高度.
【答案】解:如图,
由题意得:AB:BE=1:1.2,
∵FC∥BE,
∴AF:AB=FC:BE,即AB:BE=AF:FC=1:1.2,
∴AF:9.6=1:1.2,
∴AF=8,
∴AB=AF+FB=8+2=10.
【知识点】相似三角形的应用
【解析】【分析】由不同物体影长成正比的性质,可得AB和BE的比值,再由FC平行BE,由平行线分线段成比例的性质列比例式即可求出AF的长,则AB的长可求.
2.逻辑推理-利用相似三角形的判定和性质进行推理
4.如图,点E在菱形ABCD的边BC的延长线上,AE交CD于点F,FG∥CE交DE于点G.求证:FG=FC.
【答案】证明:四边形ABCD是菱形,
∴AB=AD,DC∥AB,AD∥BC,
∵FC∥BC,
∵FG∥AD,
∴ ,
∴
∴FG=FC
【知识点】菱形的性质;两条直线被一组平行线所截,所得的对应线段成比例
【解析】【分析】由菱形的性质可知对边平行,四条边相等,然后利用平行线分线段成比例,列出比例式,等量代换即可.
5.如图,AC是⊙O的直径,弦BD交AC于点E.
(1)求证:△ADE∽△BCE;
(2)如果AD2=AE·AC,求证:CD=CB.
【答案】证明:(1)如图∵∠A与∠B是弧CD所对的圆周角,
∴∠A=∠B,又∵∠1=∠2,
∴△ADE∽△BCE.
(2)如图,∵AD2=AE·AC,∴=,
又∵∠A=∠A,
∴△ADE∽△ACD,
∴∠AED=∠ADC,
又∵AC是⊙O的直径,
∴∠ADC=90°,
即∠AED=90°,
∴直径AC⊥BD,∴CD=CB.
【知识点】垂径定理;圆周角定理;相似三角形的判定
【解析】【分析】考查圆周角定理。
6.已知AD⊥BC,BE=CE,∠ABC=2∠C,BF为∠B的平分线.求证:AB=2DE.
【答案】解:连接EF.
∵∠ABC=2∠C,BF为∠B的平分线,
∴∠FBC=∠C=∠ABC,
∴BF=CF;
又∵BE=CE,
∴EF⊥BC;
∵AD⊥BC,
∴EF∥AD,
∴AF:FC=DE:EC;
而AB:BC=AF:FC,
∴AB:BC=DE:EC,
∴,
即AB=2DE.
【知识点】三角形的角平分线、中线和高;等腰三角形的判定与性质;两条直线被一组平行线所截,所得的对应线段成比例
【解析】【分析】连接EF.根据角平分线的性质知AF:FC=DE:EC,由平行线分线段成比例知AF:FC=DE:EC,由这两个比例式和已知条件“BE=CE”知,即AB=2DE.
3.分类讨论思想
7.如图,BA⊥MN,垂足为A,BA=4,点P是射线AN上的一个动点(点P与点A不重合),且∠BPC=∠BPA,BC⊥BP,过点C作CD⊥MN,垂足为D,设AP=x
(1)CD的长度是否随着的x变化而变化?若变化,请用含的x代数式表示CD的长度;若不变化,请求出线段CD的长度;
(2)当x取何值时,△ABP和△CDP相似.
【答案】(1)解:CD的长度不变化.
理由如下:
如图1,延长CB和PA,记交点为点Q.
∵∠BPC=∠BPA,BC⊥BP,
∴QB=BC(等腰三角形“三合一”的性质).
∵BA⊥MN,CD⊥MN,
∴AB∥CD,
∴△QAB∽△QDC,
∴ = = ,
∴CD=2AB=2×4=8,
即CD=8
(2)解:当△BAP∽△CDP时,
∵∠BPC=∠BPA,∠CPD=∠BPA,
∴∠BPA=∠BPC=∠CPD=60°,
∴AP= = = ,
即x= ;
如图2,当△BAP∽△PDC时,
∵∠CPB=∠BPA,∠PCD=∠BPA,
∴3∠BPA=90°,
∴∠BPA=30°,
∴AP= = =4 ,
即x=4 ;
即当x= 或4 时,△ABP和△CDP相似.
【知识点】相似三角形的判定
【解析】【分析】(1)如图1,延长CB和PA,记交点为点Q.根据等腰△QPC“三合一”的性质证得QB=BC;由相似三角形(△QAB∽△QDC)的对应边成比例得到 = = ,则CD=2AB;(2)当△BAP∽△CDP时,易得∠BPA=60°,x=AP= = = ,当△BAP∽△PDC时,易得∠BPA=30°,AP= = =4 ,求出x的值即可.
8.在△ABC中,D,E分别是AC,AB边上的点,AD=3,AE=2,AC=5,当AB= 时,△ADE与△ABC相似.
【答案】7.5或
【知识点】相似三角形的判定
【解析】【解答】解:如图,∵AD=3,AE=2,AC=5,
∴当△ADE∽△ACB时, = ,即 = ,解得AB= ;
当△ADE∽△ABC时, = ,即 = ,解得AB=7.5.
综上所述,当AB为7.5或 时,△ADE与△ABC相似.
故答案为:7.5或 .
【分析】根据题意画出图形,再分△ADE∽△ACB与△ADE∽△ABC两种情况进行讨论即可.
9.已知Rt△ABC中,∠C=90°,∠A≠∠B,点P是边AC上一点(不与A、C重合),过P点的一条直线与△ABC的边相交,所构成的三角形与原三角形相似,这样的直线有( )条.
A.1 B.2 C.3 D.4
【答案】D
【知识点】相似三角形的判定
【解析】【解答】解:如图,过点P作AB的平行线,或作BC的平行线,或作AB的垂线,或作∠CPD=∠B,共4条直线,
故选:D.
【分析】过点D作直线与另一边平行或垂直,或∠CPD=∠B即可.
10.如图,在四边形,,,,,.动点从点出发,沿折线以每秒3个单位长度的速度向终点运动.当点不与点A、B、重合时,作点关于直线PD的对称点,连接、,设点的运动时间为秒.
(1)线段CD的长为 ;
(2)当为直角三角形时,求的值;
(3)作点关于直线PD的对称点,连接.
①当时,求的值;
②连接,当直线经过点A时,直接写出的值.
【答案】(1)5
(2)解:分两种情况:①当点P在上时,∵点不与点A、B、重合,
∴只能是,如图所示,
当时,由(1)知,,
∴,
解得:;
②当点P在上时,∵点不与点A、B、重合,
∴只能是,过点D作于E,如图所示,
由翻折得:
由(1)知:,,,
∴
∵,
∴
∴
∴
∴
∴
∴,
∴
解得:;
综上,当为直角三角形时,的值为1或.
(3)解:①分两种情况:
1)当点P在上时,延长到F,如图所示,
由(1)知:,
∵点B与点关于对称,
∴
∵
∴
∵
∴
∴
∴,
解得:;
(3)
2)当点P在上时,延长、相交于E,延长到F,如图所示,
∵
∴
∴
∴
解得:,,
∵点B与点关于对称,
∴
∵
∴
∵
∴
∴
∴
∴
∴
解得:.
综上,当时,的值为或.
故答案为:或;
②或
【知识点】等腰三角形的判定;矩形的判定与性质;翻折变换(折叠问题);相似三角形的判定与性质
【解析】【解答】(1)解:过点D作于E,如图所示,
∵,
∴,
∵,
∴,
∵,
∴,
∴四边形是矩形,
∴,,
∴,
根据勾股定理,可得.
故答案为:5;
(3)②分两种情况:
1)当点P在上时,如图所示:
由翻折可知,点C与点关于对称,
∴,,
∵,
∴,
又∵点B与点关于对称,经过点A,
∴此时,点A为重合,则,
∴,
由股定理,得,
∴,
解得:,
∴,
∴;
2)当点P在上时,过点D作于E,于F,如图所示:
由翻折可得:,,
∴点C与点关于对称,
∵,,
∴,
∴,
∴,
由(1)知:,
∴,
∴,
∵点B与点关于对称,
∴,
∵点C与点关于对称,
∴四边形与关于对称,
∴,
∴,
∴,
∵经过点A,,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
解得:,
∴,
解得:.
综上,当直线经过点A时,的值为或.
故答案为:或.
【分析】(1)过点D作于E,先证明四边形是矩形,得,,从而得出,然后由勾股定理求解;
(2)分类讨论:①当点P在上时,;②当点P在上时,,分别求解即可;
(3)①分类讨论:1)当点P在上时,2)当点P在上时,分别求解即可;
②分类讨论:1)当点P在上时,2)当点P在上时,分别求解即可.
4.方程的思想
11.
(1)如图1,在矩形中,,,点E为边上一点,沿直线将矩形折叠,使点C落在边上的点处.求的长;
(2)如图2,展开后,将沿线段向右平移,使点的对应点与点B重合,得到,与交于点F,求线段的长;
(3)在图1中,将绕点旋转至A,,E三点共线时,请直接写出的长.
【答案】(1)解:为矩形,,,
,,
;
(2)解:为平移后的图形,,,
,,
,
设长为,
,,
解得:,
,
,,
,
,
;
(3)解:将绕点旋转至A,,E三点共线,
分以下两种情况:
①当旋转到左侧时,如图所示:
作,交的延长线于点,
由(2)可知,
由旋转性质可知,,
,
,
,
四边形为矩形,
,,
,
②当旋转到右侧时,如图所示:
作,交的延长线于点,
由(2)可知,
由旋转性质可知,,
,
,
四边形为矩形,
,,
,
.
【知识点】勾股定理;矩形的性质;矩形的判定;相似三角形的判定与性质;旋转的性质
【解析】【分析】(1)根据矩形的性质、翻折的性质和勾股定理可以直接求解;
(2)根据勾股定理,可得EB的长;根据三角形相似的判定和性质,可列比例式,求出CF的长;根据线段的计算,可得EF的长;
(3)根据旋转的角度不同,进行分类讨论;根据旋转的性质,矩形的判定和性质以及勾股定理可以直接求出DC的值.
12.如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交射线BC于点E,设AP=x.
⑴当x为何值时,△APD是等腰三角形
⑵若设BE=y,求y关于x的函数关系式;
⑶若BC的长可以变化,在现在的条件下,是否存在点P,使得PQ经过点C 若存在,求出相应的AP的长;若不存在,请说明理由,并直接写出当BC的长在什么范围内时,可以存在这样的点P,使得PQ经过点C.
【答案】解:(1)过D点作DH⊥AB于H,则四边形DHBC为矩形,
∴DH=BC=4,HB=CD=6.
∴AH=2,AD=2.
∵AP=x,
∴PH=x﹣2,
情况①:当AP=AD时,即x=2.
情况②:当AD=PD时,则AH=PH.
∴2=x﹣2,解得x=4.
情况③:当AP=PD时,
则Rt△DPH中,x2=42+(x﹣2)2,解得x=5.
∵2<x<8,
∴当x为2、4、5时,△APD是等腰三角形.
(2)∵∠DPE=∠DHP=90°,
∴∠DPH+∠EPB=∠DPH+∠HDP=90°.
∴∠HDP=∠EPB.
又∵∠DHP=∠B=90°,
∴△DPH∽△PEB.
∴=,
∴=.
整理得:y=(x﹣2)(8﹣x)=﹣x2+x﹣4;
(3)存在.
设BC=a,则由(2)得△DPH∽△PEB,
∴=,
∴y=,
当y=a时,
(8﹣x)(x﹣2)=a2
x2﹣10x+(16+a2)=0,
∴△=100﹣4(16+a2),
∵△≥0,
∴100﹣64﹣4a2≥0,
4a2≤36,
又∵a>0,
∴a≤3,
∴0<a≤3,
∴满足0<BC≤3时,存在点P,使得PQ经过C.
【知识点】一元二次方程根的判别式及应用;立体图形的初步认识;相似三角形的判定与性质
【解析】【分析】(1)过D点作DH⊥AB于H,则四边形DHBC为矩形,在Rt△AHD中,由勾股定理可求得DH、AD、PH的值,若△ADP为等腰三角形,则分三种情况:①当AP=AD时,x=AP=AD,②当AD=PD时,有AH=PH,故x=AH+PH,③当AP=PD时,则在Rt△DPH中,由勾股定理可求得DP的值,有x=AP=DP.
(2)易证:△DPH∽△PEB ,即,故可求得y与x的关系式.
(3)利用△DPH∽△PEB,得出,进而利用根的判别式和一元二次不等式解集得出即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级数学下名师点拨与训练
第27章 相似
第27章 相似 小结与复习
一、知识导图
二、知识清单
知识点一、图形的相似的概念
形状相同的图形叫做相似图形。
1)两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到;
2)全等的图形可以看成是一种特殊的相似,即不仅形状相同,大小也相同;
3)判断两个图形是否相似,就是看两个图形是不是形状相同,与其他因素无关。
例1-1.在研究相似问题时,嘉嘉和淇淇两同学的观点如下:
嘉嘉:将边长为1的正方形按图1的方式向外扩张,得到新正方形,它们的对应边间距为1,则新正方形与原正方形相似,同时也位似;
淇淇:将边长为1的正方形按图2的方式向外扩张,得到新正方形,每条对角线向其延长线两个方向各延伸1,则新正方形与原正方形相似,同时也位似.
对于两人的观点,下列说法正确的是( )
A.两人都对 B.两人都不对
C.嘉嘉对,淇淇不对 D.嘉嘉不对,淇淇对
例1-2.下列四组图形中,不是相似图形的是( )
A. B.
C. D.
变式.下列说法正确的是( )
A.对应边都成比例的多边形相似 B.对应角都相等的多边形相似
C.边数相同的正多边形相似 D.矩形都相似
知识点二、成比例线段
在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段。
1)若四条线段、、、成比例,则记作或。注意:四条线段的位置不能随意颠倒。
2)四条线段、、、的单位应一致(有时为了计算方便,、的单位一致,、的单位一致也可以)
3)判断四条线段是否成比例:①将四条线段按从小到大(或从大到小)的顺序排列;②分别计算第一和第二、第三和第四线段的比;若相等则是成比例线段,否则就不是。
4)比例的重要性质:
基本性质:若,则;反之,也成立。 和比性质:若,则;
更比性质:若,则; 反比性质:若,则;
等比性质:若,则。
5)拓展:比例式中,或中,、叫外项,、叫内项,、叫前项,、叫后项,如果,那么叫做、的比例中项。
把线段AB分成两条线段AC和BC,使AC2=AB·BC,叫做把线段AB黄金分割,C叫做线段AB的黄金分割点。
例2-1.已知四条线段a,b,c,d是成比例线段,即=,下列说法错误的是( )
A.ad=bc B.= C.= D.=
例2-2.若x是3和6的比例中项,则x的值为( )
A. B. C. D.
变式2-1.有以下命题:
①如果线段d是线段a,b,c的第四比例项,则有 .
②如果点C是线段AB的中点,那么AC是AB、BC的比例中项.
③如果点C是线段AB的黄金分割点,且AC>BC,那么AC是AB与BC的比例中项.
④如果点C是线段AB的黄金分割点,AC>BC,且AB=2,则AC=﹣1.
其中正确的判断有( )
A.1个 B.2个 C.3个 D.4个
变式2-2.已知线段a,b,c满足 ,且a+2b+c=26,则a+2b﹣c= .
知识点三、平行线分线段成比例
平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例。
推论:平行于三角形一边的直线与其他两条直线相交,截得的对应线段成比例。
例3-1.如图,已知直线,直线分别交直线于点,直线分别交直线于点,若,则的值( )
A.大于 B.等于 C.小于 D.不能确定
例3-2.如图,在中,点、为边的三等分点,点、在边上,,交于点.若,则的长为 .
变式3-1. 如图,点D、E是边 上的点,,连接,交点为F,,那么的值是 .
变式3-2.在中,,将绕点B顺时针旋转得到,其中点A,C的对应点分别为点,.当点落在的延长线上时,连接,交于点P,若是方程的两个实数根(),则的面积为 .
知识点四、相似多边形的性质与判定
(1)相似多边形对应角相等,对应边的比相等。
(2)相似比:相似多边形对应边的比称为相似比。
(3)判断两个多边形相似,必须同时具备:(1)边数相同;(2)对应角相等;(3)对应边的比相等。
例4-1.如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E、F.
求证:四边形AFGE与四边形ABCD相似.
例4-2.如图,五边形ABCDE是由五边形FGHMN经过位似变换得到的,点O是位似中心,F、G、H、M、N分别是OA、OB、OC、OD、OE的中点,则五边形ABCDE与五边形FGHMN的面积比是( )
A.2:1 B.4:1 C.5:1 D.6:1
知识点五、相似三角形的相关概念
1)、相似三角形的概念:对应角相等,对应边的比相等的两个三角形是相似三角形。
三角形相似具有传递性。
2)、相似比的概念:相似三角形对应边的比叫做相似比。相似三角形对应边的比是有顺序的。
3、相似三角形与全等三角形的关系:相似三角形不一定是全等三角形,但全等三角形一定是相似三角形。
若两个相似三角形的相似比是1,则这两个三角形是全等三角形,由此可见,全等三角形是相似三角形的一种特例。
例5 .下列说法一定正确的是( )
(A)有两边对应成比例且一角相等的两个三角形相似
(B)对应角相等的两个三角形不一定相似
(C)有两边对应成比例且夹角相等的两个三角形相似
(D)一条直线截三角形两边所得的三角形与原三角形相似
知识点六、相似三角形的判定
判定1:如果两个三角形的三组对应边的比相等,那么这两个三角形相似。
判定2:如果两个三角形的两组对应边的比相等,并且夹角相等,那么这两个三角形相似。
判定3:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
判定4:直角三角形被斜边上的高分成的两个直角三角形与原三角形都相似(此知识常用,用时需要证明)。
例6-1.如图,在四边形中,对角线、相交于点,,且,若,则的值为 .
例6-2.在中,对角线交于点O,E是上一点,且,连结,当时,若则 °,若,则 .
变式6-1.在矩形ABCD中,E为DC边上一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F处.
(1)求证:△ABF∽△FCE;
(2)若AB=8,AD=10,求EC的长.
变式6-2.如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,求FN:ND的值.
知识点七、相似三角形的性质
1、对应角相等,对应边的比相等;
2、拓展:对应高的比,对应中线的比,对应角平分线的比都等于相似比。
3、相似三角形周长的比等于相似比,面积的比等于相似比的平方。(相似多边形周长比等于相似比,相似多边形的面积比等于相似比的平方。)
例7-1.如图,在平行四边形ABCD中,点在对角线BD上,且.
(1)求证:;
(2)若,求AB的长.
例7-2. 如图,中,,,D为边上一点,.
(1)求证:;
(2)如果,求的长.
变式7-1.如图,△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在BC上,AD交PN于点E,BC=48,AD=16.
(1)若PN=18,求DE的长;
(2)若矩形PQMN的周长为80,求矩形PQMN的面积.
知识点八、利用相似三角形测高测距离
1)、利用相似三角形的性质测量河的宽度,计算不能直接测量的物体的高度或深度。
2)、利用三角形的性质来解决实际问题的核心是构造相似三角形,在构造的相似三角形中,被测物体必须是其中一边,注意要把握其余的对应边易测这一原则。
例8-1.如图,某中学两座教学楼中间有个路灯,甲、乙两个人分别在楼上观察路灯顶端,视线所及如图①所示。根据实际情况画出平面图形如图②,CD⊥DF,AB⊥DF,EF⊥DF,甲从点C可以看到点G处,乙从点E恰巧可以看到点D处,点B是DF的中点,路灯AB高5.5米,DF=120米,BG=10.5米,求甲、乙两人的观测点到地面的距离的差。
变式8-1.又到了一年中的春游季节.某班学生利用周末去参观“三军会师纪念塔”.下面是两位同学的一段对话:
甲:我站在此处看塔顶仰角为60°;
乙:我站在此处看塔顶仰角为30°;
甲:我们的身高都是1.6m;
乙:我们相距36m.
请你根据两位同学的对话,计算纪念塔的高度.(精确到1米)
变式8-2.已知如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=2m.
(1)请你画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为4m,请你计算DE的长.
知识点九、位似的概念及性质
1)两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行,象这样的两个图形叫做位似图形,这个点叫做位似中心。这时的相似比又称为位似比。
相似图形与位似图形的区别与联系:1、区别:①位似图形对应点的连线交于一点,相似图形没有;②位似图形的对应边互相平行,相似图形没有。2、联系:位似图形是特殊的相似图形。
2)相似图形与位似图形的区别与联系:
区别:①位似图形对应点的连线交于一点,相似图形没有;
②位似图形的对应边互相平行,相似图形没有。
联系:位似图形是特殊的相似图形。
3)、位似图形是特殊的相似图形,故具有相似图形的一切性质。
4)、位似图形上任意一对对应点到位似中心的距离比等于相似比。
例9-1.如图,DC∥AB,OA=2OC,则△OCD与△OAB的位似比是 .
变式9-1.如图,和是以点为位似中心的位似图形,,则和的面积比值是 .
变式9-2.如图,在平行四边形中,以C为位似中心,作平行四边形的位似平行四边形,且与原图形的位似比为2∶3,连接,若平行四边形的面积为20,则与的面积之和为 .
知识点十、利用位似变换作图(放大或缩小图形)
利用位似变换可以把一个图形放大或缩小,若位似比大于1,则通过位似变换把原图形放大;若位似比小于1,则通过位似变换把原图形缩小。
画位似图形的一般步骤:①确定位似中心;②连线并延长(分别连接位似中心和能代表原图的关键点并延长);③根据相似比确定各线段的长度;④顺次连接上述个点,得到图形。
例10-1.如图,在平面直角坐标系内,顶点坐标分别为,,.
(1)画出关于原点O成中心对称的;
(2)以A为位似中心,在网格中画出,使与位似且面积比为4:1。
变式10-1.如图,在的正方形网格中,每个小正方形的边长均为1,且每个小正方形的顶点称为格点,的顶点均在格点上,按要求完成如下画图.(要求仅用无刻度的直尺,且保留必要的画图痕迹)
(1)在图1中,以为边,画出,使与全等,为格点,请在图1中画出满足条件的所有;
(2)在图2中,以点为位似中心.画出,使与位似,且位似比,点、为格点;
(3)在图3中,在边上找一个点,且满足.
知识点十一、图形的变换与坐标
1)、平移:(1)图形沿x轴平移后,所得新图形的各对应点的纵坐标不变,当向右平移n个单位时,横坐标应相应地加n个单位,反之则减;(2)图形沿y轴平移后,所得新图形的各对应点的横坐标不变,纵坐标上加、下减。
2)、轴对称:(1)图形沿x轴翻折后所得新图形的各对应点的横坐标不变,纵坐标互为相反数;(2)图形沿y轴翻折后所得新图形的各对应点的纵坐标不变,横坐标互为相反数。
3)、以原点为位似中心的位似变换
在平面直角坐标系中,如果位似变化是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k(对应点在位似中心同侧)或者-k(对应点在位似中心异侧)。即:若设原图形的某一点的坐标为,则其位似图形对应点的坐标为或。
例11-1.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
①以O为位似中心在第二象限作位似比为1:2变换,得到对应的△A1B1C1,画出△A1B1C1,并写出C1的坐标;
②以原点O为旋转中心,画出把△ABC顺时针旋转90°的图形△A2B2C2,并写出C2的坐标.
变式11-1.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,
(2)点C1的坐标是 ;
(3)以点B为位似中心,在网格内画出△A2B2C2,
(4)使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
三、核心素养提升
数学建模-构建相似三角形模型解决实际问题
1.在《数书九章》(宋·秦九韶)中记载了一个测量塔高的问题:如图所示,表示塔的高度,表示竹竿顶端到地面的高度,表示人眼到地面的高度,、、在同一平面内,点A、C、E在一条水平直线上.已知米,米,米,米,人从点F远眺塔顶B,视线恰好经过竹竿的顶端D,可求出塔的高度.根据以上信息,塔的高度为 米.
2.如图,小李利用镜面反射原理测树高,小李在点,镜子为点,表示树,点,,在同一水平线上,小李身高米,米,米,则树高为( )
A.4米 B.5米 C.6米 D.7米
3.小亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD处,另一部分在某一建筑的墙上CD处,分别测得其长度为9.6米和2米,求旗杆AB的高度.
2.逻辑推理-利用相似三角形的判定和性质进行推理
4.如图,点E在菱形ABCD的边BC的延长线上,AE交CD于点F,FG∥CE交DE于点G.求证:FG=FC.
5.如图,AC是⊙O的直径,弦BD交AC于点E.
(1)求证:△ADE∽△BCE;
(2)如果AD2=AE·AC,求证:CD=CB.
6.已知AD⊥BC,BE=CE,∠ABC=2∠C,BF为∠B的平分线.求证:AB=2DE.
【答案】解:连接EF.
3.分类讨论思想
7.如图,BA⊥MN,垂足为A,BA=4,点P是射线AN上的一个动点(点P与点A不重合),且∠BPC=∠BPA,BC⊥BP,过点C作CD⊥MN,垂足为D,设AP=x
(1)CD的长度是否随着的x变化而变化?若变化,请用含的x代数式表示CD的长度;若不变化,请求出线段CD的长度;
(2)当x取何值时,△ABP和△CDP相似.
8.在△ABC中,D,E分别是AC,AB边上的点,AD=3,AE=2,AC=5,当AB= 时,△ADE与△ABC相似.
9.已知Rt△ABC中,∠C=90°,∠A≠∠B,点P是边AC上一点(不与A、C重合),过P点的一条直线与△ABC的边相交,所构成的三角形与原三角形相似,这样的直线有( )条.
A.1 B.2 C.3 D.4
10.如图,在四边形,,,,,.动点从点出发,沿折线以每秒3个单位长度的速度向终点运动.当点不与点A、B、重合时,作点关于直线PD的对称点,连接、,设点的运动时间为秒.
(1)线段CD的长为 ;
(2)当为直角三角形时,求的值;
(3)作点关于直线PD的对称点,连接.
①当时,求的值;
②连接,当直线经过点A时,直接写出的值.
4.方程的思想
11.
(1)如图1,在矩形中,,,点E为边上一点,沿直线将矩形折叠,使点C落在边上的点处.求的长;
(2)如图2,展开后,将沿线段向右平移,使点的对应点与点B重合,得到,与交于点F,求线段的长;
(3)在图1中,将绕点旋转至A,,E三点共线时,请直接写出的长.
12.如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交射线BC于点E,设AP=x.
⑴当x为何值时,△APD是等腰三角形
⑵若设BE=y,求y关于x的函数关系式;
⑶若BC的长可以变化,在现在的条件下,是否存在点P,使得PQ经过点C 若存在,求出相应的AP的长;若不存在,请说明理由,并直接写出当BC的长在什么范围内时,可以存在这样的点P,使得PQ经过点C.
人教版九年级数学下名师点拨与训练
第27章 相似
第27章 相似 小结与复习
一、知识导图
二、知识清单
知识点一、图形的相似的概念
形状相同的图形叫做相似图形。
1)两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到;
2)全等的图形可以看成是一种特殊的相似,即不仅形状相同,大小也相同;
3)判断两个图形是否相似,就是看两个图形是不是形状相同,与其他因素无关。
例1-1.在研究相似问题时,嘉嘉和淇淇两同学的观点如下:
嘉嘉:将边长为1的正方形按图1的方式向外扩张,得到新正方形,它们的对应边间距为1,则新正方形与原正方形相似,同时也位似;
淇淇:将边长为1的正方形按图2的方式向外扩张,得到新正方形,每条对角线向其延长线两个方向各延伸1,则新正方形与原正方形相似,同时也位似.
对于两人的观点,下列说法正确的是( )
A.两人都对 B.两人都不对
C.嘉嘉对,淇淇不对 D.嘉嘉不对,淇淇对
【答案】A
【知识点】图形的相似;位似图形的概念
例1-2.下列四组图形中,不是相似图形的是( )
A. B.
C. D.
【答案】D
【知识点】图形的相似
【解析】【解答】解:A、形状相同,但大小不同,符合相似形的定义,故不符合题意;
B、形状相同,但大小不同,符合相似形的定义,故不符合题意;
C、形状相同,但大小不同,符合相似形的定义,故不符合题意;
D、形状不相同,不符合相似形的定义,故符合题意;
故选:D.
【分析】根据相似图形的定义,对选项进行一一分析,排除错误答案.
变式.下列说法正确的是( )
A.对应边都成比例的多边形相似 B.对应角都相等的多边形相似
C.边数相同的正多边形相似 D.矩形都相似
【答案】C
【知识点】图形的相似
【解析】【分析】根据相似图形的定义,对选项一一分析,排除错误答案。
【解答】A、对应边都成比例的多边形,属于形状不唯一确定的图形,故错误;
B、对应角都相等的多边形,属于形状不唯一确定的图形,故错误;
C、边数相同的正多边形,形状相同,大小不一定相同,故正确;
D、矩形属于形状不唯一确定的图形,故错误。
故选C.
【点评】本题考查相似变换的定义,即图形的形状相同,但大小不一定相同的是相似形。
知识点二、成比例线段
在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段。
1)若四条线段、、、成比例,则记作或。注意:四条线段的位置不能随意颠倒。
2)四条线段、、、的单位应一致(有时为了计算方便,、的单位一致,、的单位一致也可以)
3)判断四条线段是否成比例:①将四条线段按从小到大(或从大到小)的顺序排列;②分别计算第一和第二、第三和第四线段的比;若相等则是成比例线段,否则就不是。
4)比例的重要性质:
基本性质:若,则;反之,也成立。 和比性质:若,则;
更比性质:若,则; 反比性质:若,则;
等比性质:若,则。
5)拓展:比例式中,或中,、叫外项,、叫内项,、叫前项,、叫后项,如果,那么叫做、的比例中项。
把线段AB分成两条线段AC和BC,使AC2=AB·BC,叫做把线段AB黄金分割,C叫做线段AB的黄金分割点。
例2-1.已知四条线段a,b,c,d是成比例线段,即=,下列说法错误的是( )
A.ad=bc B.= C.= D.=
【答案】C
【知识点】比例线段
【解析】【分析】根据比例的性质将原式变形,分别进行判断即可,进而得出答案.
【解答】∵四条线段a,b,c,d是成比例线段,即=,
∴A.利用内项之积等于外项之积,ad=bc,故选项正确,
B.利用内项之积等于外项之积,a(b+d)=b(a+c),ab+ad=ab+bc,即ad=bc,故选项正确,
C.∵=,
∴=,故选项错误,
D.∵=∴=,故选项正确.
故选:C.
【点评】此题主要考查了比例的性质,将比例式灵活正确变形得出是解题关键.
例2-2.若x是3和6的比例中项,则x的值为( )
A. B. C. D.
【答案】D
【知识点】比例线段
【解析】【分析】根据比例中项的概念,得x2=3×6,则x可求出来.
【解答】∵x是3和6的比例中项,
∴x2=3×6=18,
解得x=.
故选D.
【点评】本题考查了比例中项的概念:当比例式中的两个内项相同时,即叫比例中项.求比例中项根据比例的基本性质进行计算.
变式2-1.有以下命题:
①如果线段d是线段a,b,c的第四比例项,则有 .
②如果点C是线段AB的中点,那么AC是AB、BC的比例中项.
③如果点C是线段AB的黄金分割点,且AC>BC,那么AC是AB与BC的比例中项.
④如果点C是线段AB的黄金分割点,AC>BC,且AB=2,则AC=﹣1.
其中正确的判断有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【知识点】比例线段;黄金分割
【解析】【解答】解:①、根据第四比例项的概念,显然正确;
②、如果点C是线段AB的中点,AB:AC=2,AC:BC=1,不成比例,错误;
③、根据黄金分割的概念,正确;
④、根据黄金分割的概念:AC= ﹣1,错误.
故选B.
【分析】根据比例中项和黄金分割的概念分析各个说法.
变式2-2.已知线段a,b,c满足 ,且a+2b+c=26,则a+2b﹣c= .
【答案】2
【知识点】比例线段
【解析】【解答】解:设 =k,则有a=3k,b=2k,c=6k,
代入已知等式得:3k+4k+6k=26,
解得:k=2,即a=6,b=4,c=12,
则原式=6+8﹣12=2,
故答案为:2
【分析】设已知比例式值为k,表示出a,b,c,代入已知等式求出k的值,确定出a,b,c的值,代入原式计算即可得到结果.
知识点三、平行线分线段成比例
平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例。
推论:平行于三角形一边的直线与其他两条直线相交,截得的对应线段成比例。
例3-1.如图,已知直线,直线分别交直线于点,直线分别交直线于点,若,则的值( )
A.大于 B.等于 C.小于 D.不能确定
【答案】A
【知识点】平行四边形的判定与性质;两条直线被一组平行线所截,所得的对应线段成比例
【解析】【解答】解:作分别交、于、,
∵,
∴四边形、四边形是平行四边形,
,
,
,即,
故答案为:A.
【分析】作分别交、于、,可得四边形、四边形是平行四边形,,然后根据平行线分线段成比例求出,再进一步计算的值即可.
例3-2.如图,在中,点、为边的三等分点,点、在边上,,交于点.若,则的长为 .
【答案】
【知识点】平行线的判定与性质;两条直线被一组平行线所截,所得的对应线段成比例;相似三角形的判定与性质
【解析】【解答】点,为边的三等分点,
∴BE=ED=AD,
,
,
,
,
,
点,为边的三等分点,,
点,为边的三等分点,
,
,
,
.
故答案为:。
【分析】先证出,再利用相似三角形的性质求得的长度,利用平行线分线段成比例定理求得,最后利用相似三角形的判定与性质解答即可得出结论.
变式3-1. 如图,点D、E是边 上的点,,连接,交点为F,,那么的值是 .
【答案】
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
【解析】【解答】解:过作,交于,如图所示:
则,即:,,
,即:,
∴.
故答案为:
【分析】过作,交于,进而根据平行线分线段成比例结合题意即可求解。
变式3-2.在中,,将绕点B顺时针旋转得到,其中点A,C的对应点分别为点,.当点落在的延长线上时,连接,交于点P,若是方程的两个实数根(),则的面积为 .
【答案】
【知识点】因式分解法解一元二次方程;两条直线被一组平行线所截,所得的对应线段成比例;旋转的性质
【解析】【解答】解:作交于,过作于,
∵是方程的两个实数根(),
∴,,
∴,
∵将绕点B顺时针旋转得到,
∴,,,,
∵
∴,
∴,
∵
∴,
∴,
∴,
∴,
∴,
∵
∴,
∴,解得,
∴,
∴,
∴,
故答案为:.
【分析】 先解方程可得AC=4,BC=3,再作CM∥BP交AB于点M,过C作CD⊥AB于点D,即可求出CD、BD的长度,再由旋转的性质和平行线的性质可得∠CBA=∠CMB,即可得到CM=BC,MD=BD,再由平行线分线段成比例求出BP,最后根据求解即可.
知识点四、相似多边形的性质与判定
(1)相似多边形对应角相等,对应边的比相等。
(2)相似比:相似多边形对应边的比称为相似比。
(3)判断两个多边形相似,必须同时具备:(1)边数相同;(2)对应角相等;(3)对应边的比相等。
例4-1.如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E、F.
求证:四边形AFGE与四边形ABCD相似.
【答案】证明:∵四边形ABCD是正方形,AC是对角线,
∴∠DAC=∠BAC=45°.
又∵GE⊥AD,GF⊥AB,
∴EG=FG,且AE=EG,AF=FG.
∴AE=EG=FG=AF,
即四边形AFGE为正方形.
∴ = = = ,且∠EAF=∠DAB,∠AFG=∠ABC,∠FGE=∠BCD,∠AEG=∠ADC.
∴四边形AFGE与四边形ABCD相似
【知识点】相似多边形
【解析】【分析】由正方形的性质可知;AC平分∠DAB,然后由角平分线的性质可知GE=GF,从而可证明四边形EGFA为正方形,故此四边形AFGE与四边形ABCD相似.本题主要考查的是相似多边形的判定、正方形的判定、角平分线的性质,证得四边形EAFG为正方形是解题的关键.
例4-2.如图,五边形ABCDE是由五边形FGHMN经过位似变换得到的,点O是位似中心,F、G、H、M、N分别是OA、OB、OC、OD、OE的中点,则五边形ABCDE与五边形FGHMN的面积比是( )
A.2:1 B.4:1 C.5:1 D.6:1
【答案】B
【知识点】相似多边形;位似变换
【解析】【解答】解:∵F为AO的中点,
∴OF:OA=1:2,
∵ 五边形ABCDE是由五边形FGHMN经过位似变换得到的 ,
∴FN∥AE,
∴△OFN∽△OAE,
∴OF∶OA=FN∶AE=1∶2
∴五边形ABCDE与五边形FGHMN的面积比为:4:1.
故答案为:B.
【分析】由五边形ABCDE与五边形FGHMN关于点O成位似关系,且OF:OA=1:2,可得位似比为1:2,根据形似图形的面积比等于相似比的平方,即可求得答案.
知识点五、相似三角形的相关概念
1)、相似三角形的概念:对应角相等,对应边的比相等的两个三角形是相似三角形。
三角形相似具有传递性。
2)、相似比的概念:相似三角形对应边的比叫做相似比。相似三角形对应边的比是有顺序的。
3、相似三角形与全等三角形的关系:相似三角形不一定是全等三角形,但全等三角形一定是相似三角形。
若两个相似三角形的相似比是1,则这两个三角形是全等三角形,由此可见,全等三角形是相似三角形的一种特例。
例5 .下列说法一定正确的是( )
(A)有两边对应成比例且一角相等的两个三角形相似
(B)对应角相等的两个三角形不一定相似
(C)有两边对应成比例且夹角相等的两个三角形相似
(D)一条直线截三角形两边所得的三角形与原三角形相似
【答案】C
【解析】根据判定定理2可知A错误,C正确;根据判定定理1可知B错误,根据相似三 角形预备定理可知只有直线与底边平行时才相似.
【总结】考查相似三角形的判定定理掌握情况和相关条件.
知识点六、相似三角形的判定
判定1:如果两个三角形的三组对应边的比相等,那么这两个三角形相似。
判定2:如果两个三角形的两组对应边的比相等,并且夹角相等,那么这两个三角形相似。
判定3:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
判定4:直角三角形被斜边上的高分成的两个直角三角形与原三角形都相似(此知识常用,用时需要证明)。
例6-1.如图,在四边形中,对角线、相交于点,,且,若,则的值为 .
【答案】
【知识点】相似三角形的判定;解直角三角形—边角关系
【解析】【解答】解:如图:
过点D作DE⊥BC于点E.
∴,
设DE=3x,DB=5x,则BE=4x.
∵DC=DB=5x,
∴CE=BE=4x,BC=8x.
过点A作AG//BC交DB于点G,
∴,∠AHD=∠CEH=90°=∠AHE.
∵,
∴∠GAD=∠GAB=∠ABC.
∴△DAH∽△ABC.
∴.
∵,
∴四边形ACEH是矩形,
∴.
∴
故答案为:.
【分析】过点D作DE⊥BC于点E.根据 ,设DE=3x,结合DC=DB可表示出BE,CE,BD.过点A作AG//BC交DB于点G,根据可证得∠GAD=∠GAB=∠ABC以及∠AHD=∠CEH=90°=∠AHE.可得△DAH∽△ABC和四边形ACEH是矩形,于是可得,可得结果.
例6-2.在中,对角线交于点O,E是上一点,且,连结,当时,若则 °,若,则 .
【答案】;
【知识点】相似三角形的性质;相似三角形的判定;四边形的综合
【解析】【解答】解:∵四边形ABCD是平行四边形,
∴AB//CD,∠BCD=∠BAD.
∵
∴,
∴∠AED=∠BAE=90°,
①∵,,AD=DA,
∴△OAD≌△EDA(SAS)
∴∠AOD=∠AED=90°,∠ODA=∠EAD.
∴AC⊥BD,
∴ 是菱形.
∴AB=BC=CD=AD.
∴∠ODC=∠ODA=∠EAD.
∵在直角三角形AED中,∠EAD+∠ODA+∠ODC=3∠EAD=90°.
∴∠ABC=∠ADC=60°.
②在DE上选取点F,使EF=CE,连接AF. 如图所示:
∵AE⊥CF,
∴AC=AF,
∴∠CAE=∠FAE,∠ACE=∠AFE.
∴.
∵∠OCD=∠FCA,
∴△OCD∽△FCA.
∴
∵AO=CO=DE,
∴
令,
∴.
解得:(舍负)
故
故答案为:60°;.
【分析】先根据平行四边形的性质以及角的换算,得出∠AED=90°,再证明△OAD≌△EDA ( SAS) ,得∠AOD=∠AED=90°,∠ODA=∠EAD.于是可得四边形ABCD为菱形,根据菱形的对角线平分对角和直角三角形两锐角互余,得3∠EAD=90°,可求∠ABC的度数;
在DE上选取点F,使EF=CE,连接AF.根据线段垂直平分线的性质得AC=AF,于是可证明△OCD∽△FCA,得,结合AO=CO=DE,可得,令,得到关于x的方程,求解即可.
变式6-1.在矩形ABCD中,E为DC边上一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F处.
(1)求证:△ABF∽△FCE;
(2)若AB=8,AD=10,求EC的长.
【答案】(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,
∴∠BAF+∠AFB=90°,
由翻折可得:
∠D=∠AFE=90°,
∴∠AFB+∠EFC=90°,
∴∠BAF=∠EFC,
∵∠B=∠C,
∴△ABF∽△FCE;
(2)解:∵四边形ABCD是矩形,AD=10,
∴BC=10,
由翻折可得:
AF=10,
在Rt△ABF中,
,
∴CF=10﹣6=4,
∵△ABF∽△FCE,
∴,
∴,
∴CE=3.
【知识点】矩形的性质;翻折变换(折叠问题);相似三角形的判定
【解析】【分析】(1)根据四边形ABCD是矩形,得出∠B=∠C=∠D=90°,由翻折可得:∠D=∠AFE=90°,利用同角的余角相等可以得出∠BAF=∠EFC,即可证出结论;
(2)由翻折可得:AF=10,根据勾股定理得出BF=6,利用 △ABF∽△FCE ,求解即可EC.
变式6-2.如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,求FN:ND的值.
【答案】解:过点F作FE∥BD,交AC于点E,∴,∵AF:BF=1:2,∴=,∴,即FE=BC,∵BC:CD=2:1,∴CD=BC,∵FE∥BD,∴.即FN:ND=2:3.
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
【解析】【分析】过点F作FE∥BD,交AC于点E,求出,得出FE=BC,根据已知推出CD=BC,根据平行线分线段成比例定理推出=,代入化简即可.本题考查了平行线分线段成比例定理的应用,注意:平行线分的线段对应成比例,此题具有一定的代表性,但是一定比较容易出错的题目.
知识点七、相似三角形的性质
1、对应角相等,对应边的比相等;
2、拓展:对应高的比,对应中线的比,对应角平分线的比都等于相似比。
3、相似三角形周长的比等于相似比,面积的比等于相似比的平方。(相似多边形周长比等于相似比,相似多边形的面积比等于相似比的平方。)
例7-1.如图,在平行四边形ABCD中,点在对角线BD上,且.
(1)求证:;
(2)若,求AB的长.
【答案】(1)证明:∵四边形ABCD为平行四边形,
,
(2)解:
.
【知识点】平行四边形的性质;相似三角形的判定与性质
【解析】【分析】(1)根据平行四边形的性质,推出从而证明;
(2)根据相似三角形对应边成比例,列出比例式,即可求出AB长.
例7-2. 如图,中,,,D为边上一点,.
(1)求证:;
(2)如果,求的长.
【答案】(1)证明:∵,,
∴,
∵,
∴
(2)解:∵,
∴
∴,
∵,
∴.
【知识点】相似三角形的判定与性质
【解析】【分析】(1)根据相似三角形的判定,对应边成比例且夹角相等证出即可.
(2)根据相似三角形对应边成比例求解即可.
变式7-1.如图,△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在BC上,AD交PN于点E,BC=48,AD=16.
(1)若PN=18,求DE的长;
(2)若矩形PQMN的周长为80,求矩形PQMN的面积.
【答案】(1)解:依题意得:PN∥BC,则△APN∽△ABC,
又AD是高,则,
设DE=,则AE=16-,
由得,,解之得,=10
(2)解:由矩形PQMN,又AD是高,则四边形PQDE为矩形,
∴DE=PQ,
设DE=PQ=,则PN=,
同理得,
解得=4
则矩形PQMN的面积=
【知识点】矩形的判定与性质;相似三角形的判定与性质
【解析】【分析】(1)先根据相似三角形的判定与性质证明△APN∽△ABC得到,设DE=,则AE=16-,进而代入即可求解;
(2)先根据矩形的判定与性质得到DE=PQ,设DE=PQ=,则PN=,进而求出y,再根据矩形的面积公式即可求解。
知识点八、利用相似三角形测高测距离
1)、利用相似三角形的性质测量河的宽度,计算不能直接测量的物体的高度或深度。
2)、利用三角形的性质来解决实际问题的核心是构造相似三角形,在构造的相似三角形中,被测物体必须是其中一边,注意要把握其余的对应边易测这一原则。
例8-1.如图,某中学两座教学楼中间有个路灯,甲、乙两个人分别在楼上观察路灯顶端,视线所及如图①所示。根据实际情况画出平面图形如图②,CD⊥DF,AB⊥DF,EF⊥DF,甲从点C可以看到点G处,乙从点E恰巧可以看到点D处,点B是DF的中点,路灯AB高5.5米,DF=120米,BG=10.5米,求甲、乙两人的观测点到地面的距离的差。
【答案】解:∵AB⊥DF,EF⊥DF,
∴∠ABD=∠F=90°,
又∵∠EDF=∠ADB,
∴△DAB~△DEF,
同理得△GAB~△GCD,
∵点B是DF的中点,
∴DB=BF= DF= ×120=60,
∵
∴EF=2AB=2x5.5=11,
∵BG=10.5,
∴DG=10.5+60=70.5
∴CD= AB= ×55≈36.9
∴甲、乙两人的观察点到地面的距离的差为:36.9-11=25.9(米)
【知识点】相似三角形的应用
【解析】【分析】利用垂直的定义可证∠ABD=∠F,再利用有两组对应角相等的两三角形相似,可证得△DAB~△DEF,同理得△GAB~△GCD,再利用相似三角形的对应边成比例,就可求出EF,DG的长,然后求出CD的长即甲、乙两人的观测点到地面的距离的差。
变式8-1.又到了一年中的春游季节.某班学生利用周末去参观“三军会师纪念塔”.下面是两位同学的一段对话:
甲:我站在此处看塔顶仰角为60°;
乙:我站在此处看塔顶仰角为30°;
甲:我们的身高都是1.6m;
乙:我们相距36m.
请你根据两位同学的对话,计算纪念塔的高度.(精确到1米)
【答案】解:如图,CD=EF=BH=1.6m,CE=DF=36m,∠ADH=30°,∠AFH=30°,
在Rt△AHF中,∵tan∠AFH=,
∴FH=,
在Rt△ADH中,∵tan∠ADH=,
∴DH=,
而DH﹣FH=DF,
∴﹣=36,即﹣=36,
∴AH=18,
∴AB=AH+BH=18+1.6≈33(m).
答:纪念塔的高度约为33m.
【知识点】相似三角形的应用
【解析】【分析】先画出几何图形,如图,CD=EF=BH=1.6m,CE=DF=36m,∠ADH=30°,∠AFH=30°,分别利用正切定义得到FH=,DH=,则﹣=36,再利用特殊角的函数值可计算出AH=18,然后计算AH+BH即可.
变式8-2.已知如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=2m.
(1)请你画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为4m,请你计算DE的长.
【答案】解:(1)如图,EF为此时DE在阳光下的投影;
(2)∵AC∥DF,
∴∠ACB=∠DFE,
∴Rt△ABC∽Rt△DEF,
∴,即,解得DE=10(m),
即DE的长为10m.
【知识点】相似三角形的应用;平行投影
【解析】【分析】(1)连结AC,过点D作DF∥AC,则EF为所求;
(2)先证明Rt△ABC∽Rt△DEF,然后利用相似比计算出DE的长.
知识点九、位似的概念及性质
1)两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行,象这样的两个图形叫做位似图形,这个点叫做位似中心。这时的相似比又称为位似比。
相似图形与位似图形的区别与联系:1、区别:①位似图形对应点的连线交于一点,相似图形没有;②位似图形的对应边互相平行,相似图形没有。2、联系:位似图形是特殊的相似图形。
2)相似图形与位似图形的区别与联系:
区别:①位似图形对应点的连线交于一点,相似图形没有;
②位似图形的对应边互相平行,相似图形没有。
联系:位似图形是特殊的相似图形。
3)、位似图形是特殊的相似图形,故具有相似图形的一切性质。
4)、位似图形上任意一对对应点到位似中心的距离比等于相似比。
例9-1.如图,DC∥AB,OA=2OC,则△OCD与△OAB的位似比是 .
【答案】1:2
【知识点】位似变换
【解析】解:∵DC∥AB
∴△OAB∽△OCD
∵△OCD与OAB的对应点的连线都过点O
∴△OCD与△OAB的位似
∴△OCD与△OAB的位似比为OC:OA=1:2.
【分析】先证明△OAB∽△OCD,△OCD与OAB的对应点的连线都过点O,所以可得△OCD与△OAB的位似,即可求得△OCD与△OAB的位似比为OC:OA=1:2.
变式9-1.如图,和是以点为位似中心的位似图形,,则和的面积比值是 .
【答案】
【知识点】相似三角形的性质;位似变换
【解析】【解答】解:∵△ABC和△DEF是以点O为位似中心的位似图形,
∴△ABC∽△DEF,
∵OA:OD=2:3,
∴AB:DE=2:3,
∴.
故答案为:.
【分析】根据位似的性质得△ABC∽△DEF,由已知OA:OD=2:3,得AB:DE=2:3,根据相似三角形的性质得,即可求解.
变式9-2.如图,在平行四边形中,以C为位似中心,作平行四边形的位似平行四边形,且与原图形的位似比为2∶3,连接,若平行四边形的面积为20,则与的面积之和为 .
【答案】10
【知识点】平行四边形的性质;位似变换
【解析】【解答】解:连接,如图所示:
∵平行四边形和平行四边形是位似图形,且位似比为2∶3,
∴,,
∴,,
∴,,
∴,
∴,
故答案为:10
【分析】连接,先根据位似结合题意得到,,进而得到,,再根据“”即可求解。
知识点十、利用位似变换作图(放大或缩小图形)
利用位似变换可以把一个图形放大或缩小,若位似比大于1,则通过位似变换把原图形放大;若位似比小于1,则通过位似变换把原图形缩小。
画位似图形的一般步骤:①确定位似中心;②连线并延长(分别连接位似中心和能代表原图的关键点并延长);③根据相似比确定各线段的长度;④顺次连接上述个点,得到图形。
例10-1.如图,在平面直角坐标系内,顶点坐标分别为,,.
(1)画出关于原点O成中心对称的;
(2)以A为位似中心,在网格中画出,使与位似且面积比为4:1。
【答案】(1)解:如图,即为所求作的三角形;
(2)解:如图,与即为所求作的三角形.
【知识点】作图﹣位似变换;作图﹣旋转
【解析】【分析】(1)根据对称性质作出A、B、C关于原点的对称点A1、B1、C1,顺次连接即可;
(2)根据位似图形的性质得出对应点位置,再顺次连接即可求解.
变式10-1.如图,在的正方形网格中,每个小正方形的边长均为1,且每个小正方形的顶点称为格点,的顶点均在格点上,按要求完成如下画图.(要求仅用无刻度的直尺,且保留必要的画图痕迹)
(1)在图1中,以为边,画出,使与全等,为格点,请在图1中画出满足条件的所有;
(2)在图2中,以点为位似中心.画出,使与位似,且位似比,点、为格点;
(3)在图3中,在边上找一个点,且满足.
【答案】(1)解:如图,和和即为所作,
;
(2)解:如图,即为所作,
;
(3)解:如图所示,取格点,,连接,交于点,则点即为所求作的点.
【知识点】作图﹣位似变换;尺规作图-作三角形
【解析】【分析】
(1)根据全等三角形的性质即可作出;
(2)根据位似图形的性质以及相似三角形的性质即可画出△EFC;
(3)取格点E,F,连接EF,交AC于P点,则点P即为所求作的点,由图可得△APF∽△CPE,从而得出.
知识点十一、图形的变换与坐标
1)、平移:(1)图形沿x轴平移后,所得新图形的各对应点的纵坐标不变,当向右平移n个单位时,横坐标应相应地加n个单位,反之则减;(2)图形沿y轴平移后,所得新图形的各对应点的横坐标不变,纵坐标上加、下减。
2)、轴对称:(1)图形沿x轴翻折后所得新图形的各对应点的横坐标不变,纵坐标互为相反数;(2)图形沿y轴翻折后所得新图形的各对应点的纵坐标不变,横坐标互为相反数。
3)、以原点为位似中心的位似变换
在平面直角坐标系中,如果位似变化是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k(对应点在位似中心同侧)或者-k(对应点在位似中心异侧)。即:若设原图形的某一点的坐标为,则其位似图形对应点的坐标为或。
例11-1.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
①以O为位似中心在第二象限作位似比为1:2变换,得到对应的△A1B1C1,画出△A1B1C1,并写出C1的坐标;
②以原点O为旋转中心,画出把△ABC顺时针旋转90°的图形△A2B2C2,并写出C2的坐标.
【答案】解:①如图所示:△A1B1C1,即为所求,
C1的坐标为:(﹣8,2);
②如图所示:△A2B2C2,即为所求,
C2的坐标为:(﹣1,﹣4).
【知识点】作图﹣位似变换
【解析】【分析】①直接利用位似图形的性质得出对应点位置进而得出答案;②直接利用旋转的性质得出对应点位置,进而得出答案.
变式11-1.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,
(2)点C1的坐标是 ;
(3)以点B为位似中心,在网格内画出△A2B2C2,
(4)使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
【答案】(1)如图△A1B1C1
(2)(2,﹣2)
(3)如图△A2B2C2
(4)(1,0)
【知识点】作图﹣位似变换
【解析】【解答】解:(1.)如图所示,画出△ABC向下平移4个单位长度得到的△A1B1C1,
(2.)点C1的坐标是(2,﹣2);
(3.)如图所示,以B为位似中心,画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,
(4.)点C2的坐标是(1,0),
【分析】(1)将△ABC向下平移4个单位长度得到的△A1B1C1,如图所示,(2)找出所求点坐标即可;(3)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,如图所示,(4)找出所求点坐标即可.
三、核心素养提升
数学建模-构建相似三角形模型解决实际问题
1.在《数书九章》(宋·秦九韶)中记载了一个测量塔高的问题:如图所示,表示塔的高度,表示竹竿顶端到地面的高度,表示人眼到地面的高度,、、在同一平面内,点A、C、E在一条水平直线上.已知米,米,米,米,人从点F远眺塔顶B,视线恰好经过竹竿的顶端D,可求出塔的高度.根据以上信息,塔的高度为 米.
【答案】
【知识点】相似三角形的应用
【解析】【解答】解:如图,过作于,交于,
则,,,,
∴,
∵,
∴,
∴,
∴,解得:,
∴(米),
故答案为:.
【分析】本题根据相似三角形的预备定理:得出,再根据相似三角形的性质:对应边成比例,列出比例式:,求出QB,再通过计算出AB即可.
2.如图,小李利用镜面反射原理测树高,小李在点,镜子为点,表示树,点,,在同一水平线上,小李身高米,米,米,则树高为( )
A.4米 B.5米 C.6米 D.7米
【答案】A
【知识点】相似三角形的应用;一线三等角相似模型(K字型相似模型)
【解析】【解答】解:根据题意可知: ∠CAO=∠DBO=90°,∠COF=∠DOF,
故∠COA+∠COF=90°,∠DOB+∠DOF=90°,
∴∠COA=∠DOB,
∴△ACO∽△BDO,
∴,
∵AC=1.6米,OA=2.4米,OB=6米,
∴,
解得: BD=4,
即树高为4米.
故答案为:A.
【分析】根据等角的余角相等得出∠COA=∠DOB,根据有两个角相等的两个三角形是相似三角形得出△ACO∽△BDO,根据相似三角形的对应边之比相等,即可代入数据,求出BD的值.
3.小亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD处,另一部分在某一建筑的墙上CD处,分别测得其长度为9.6米和2米,求旗杆AB的高度.
【答案】解:如图,
由题意得:AB:BE=1:1.2,
∵FC∥BE,
∴AF:AB=FC:BE,即AB:BE=AF:FC=1:1.2,
∴AF:9.6=1:1.2,
∴AF=8,
∴AB=AF+FB=8+2=10.
【知识点】相似三角形的应用
【解析】【分析】由不同物体影长成正比的性质,可得AB和BE的比值,再由FC平行BE,由平行线分线段成比例的性质列比例式即可求出AF的长,则AB的长可求.
2.逻辑推理-利用相似三角形的判定和性质进行推理
4.如图,点E在菱形ABCD的边BC的延长线上,AE交CD于点F,FG∥CE交DE于点G.求证:FG=FC.
【答案】证明:四边形ABCD是菱形,
∴AB=AD,DC∥AB,AD∥BC,
∵FC∥BC,
∵FG∥AD,
∴ ,
∴
∴FG=FC
【知识点】菱形的性质;两条直线被一组平行线所截,所得的对应线段成比例
【解析】【分析】由菱形的性质可知对边平行,四条边相等,然后利用平行线分线段成比例,列出比例式,等量代换即可.
5.如图,AC是⊙O的直径,弦BD交AC于点E.
(1)求证:△ADE∽△BCE;
(2)如果AD2=AE·AC,求证:CD=CB.
【答案】证明:(1)如图∵∠A与∠B是弧CD所对的圆周角,
∴∠A=∠B,又∵∠1=∠2,
∴△ADE∽△BCE.
(2)如图,∵AD2=AE·AC,∴=,
又∵∠A=∠A,
∴△ADE∽△ACD,
∴∠AED=∠ADC,
又∵AC是⊙O的直径,
∴∠ADC=90°,
即∠AED=90°,
∴直径AC⊥BD,∴CD=CB.
【知识点】垂径定理;圆周角定理;相似三角形的判定
【解析】【分析】考查圆周角定理。
6.已知AD⊥BC,BE=CE,∠ABC=2∠C,BF为∠B的平分线.求证:AB=2DE.
【答案】解:连接EF.
∵∠ABC=2∠C,BF为∠B的平分线,
∴∠FBC=∠C=∠ABC,
∴BF=CF;
又∵BE=CE,
∴EF⊥BC;
∵AD⊥BC,
∴EF∥AD,
∴AF:FC=DE:EC;
而AB:BC=AF:FC,
∴AB:BC=DE:EC,
∴,
即AB=2DE.
【知识点】三角形的角平分线、中线和高;等腰三角形的判定与性质;两条直线被一组平行线所截,所得的对应线段成比例
【解析】【分析】连接EF.根据角平分线的性质知AF:FC=DE:EC,由平行线分线段成比例知AF:FC=DE:EC,由这两个比例式和已知条件“BE=CE”知,即AB=2DE.
3.分类讨论思想
7.如图,BA⊥MN,垂足为A,BA=4,点P是射线AN上的一个动点(点P与点A不重合),且∠BPC=∠BPA,BC⊥BP,过点C作CD⊥MN,垂足为D,设AP=x
(1)CD的长度是否随着的x变化而变化?若变化,请用含的x代数式表示CD的长度;若不变化,请求出线段CD的长度;
(2)当x取何值时,△ABP和△CDP相似.
【答案】(1)解:CD的长度不变化.
理由如下:
如图1,延长CB和PA,记交点为点Q.
∵∠BPC=∠BPA,BC⊥BP,
∴QB=BC(等腰三角形“三合一”的性质).
∵BA⊥MN,CD⊥MN,
∴AB∥CD,
∴△QAB∽△QDC,
∴ = = ,
∴CD=2AB=2×4=8,
即CD=8
(2)解:当△BAP∽△CDP时,
∵∠BPC=∠BPA,∠CPD=∠BPA,
∴∠BPA=∠BPC=∠CPD=60°,
∴AP= = = ,
即x= ;
如图2,当△BAP∽△PDC时,
∵∠CPB=∠BPA,∠PCD=∠BPA,
∴3∠BPA=90°,
∴∠BPA=30°,
∴AP= = =4 ,
即x=4 ;
即当x= 或4 时,△ABP和△CDP相似.
【知识点】相似三角形的判定
【解析】【分析】(1)如图1,延长CB和PA,记交点为点Q.根据等腰△QPC“三合一”的性质证得QB=BC;由相似三角形(△QAB∽△QDC)的对应边成比例得到 = = ,则CD=2AB;(2)当△BAP∽△CDP时,易得∠BPA=60°,x=AP= = = ,当△BAP∽△PDC时,易得∠BPA=30°,AP= = =4 ,求出x的值即可.
8.在△ABC中,D,E分别是AC,AB边上的点,AD=3,AE=2,AC=5,当AB= 时,△ADE与△ABC相似.
【答案】7.5或
【知识点】相似三角形的判定
【解析】【解答】解:如图,∵AD=3,AE=2,AC=5,
∴当△ADE∽△ACB时, = ,即 = ,解得AB= ;
当△ADE∽△ABC时, = ,即 = ,解得AB=7.5.
综上所述,当AB为7.5或 时,△ADE与△ABC相似.
故答案为:7.5或 .
【分析】根据题意画出图形,再分△ADE∽△ACB与△ADE∽△ABC两种情况进行讨论即可.
9.已知Rt△ABC中,∠C=90°,∠A≠∠B,点P是边AC上一点(不与A、C重合),过P点的一条直线与△ABC的边相交,所构成的三角形与原三角形相似,这样的直线有( )条.
A.1 B.2 C.3 D.4
【答案】D
【知识点】相似三角形的判定
【解析】【解答】解:如图,过点P作AB的平行线,或作BC的平行线,或作AB的垂线,或作∠CPD=∠B,共4条直线,
故选:D.
【分析】过点D作直线与另一边平行或垂直,或∠CPD=∠B即可.
10.如图,在四边形,,,,,.动点从点出发,沿折线以每秒3个单位长度的速度向终点运动.当点不与点A、B、重合时,作点关于直线PD的对称点,连接、,设点的运动时间为秒.
(1)线段CD的长为 ;
(2)当为直角三角形时,求的值;
(3)作点关于直线PD的对称点,连接.
①当时,求的值;
②连接,当直线经过点A时,直接写出的值.
【答案】(1)5
(2)解:分两种情况:①当点P在上时,∵点不与点A、B、重合,
∴只能是,如图所示,
当时,由(1)知,,
∴,
解得:;
②当点P在上时,∵点不与点A、B、重合,
∴只能是,过点D作于E,如图所示,
由翻折得:
由(1)知:,,,
∴
∵,
∴
∴
∴
∴
∴
∴,
∴
解得:;
综上,当为直角三角形时,的值为1或.
(3)解:①分两种情况:
1)当点P在上时,延长到F,如图所示,
由(1)知:,
∵点B与点关于对称,
∴
∵
∴
∵
∴
∴
∴,
解得:;
(3)
2)当点P在上时,延长、相交于E,延长到F,如图所示,
∵
∴
∴
∴
解得:,,
∵点B与点关于对称,
∴
∵
∴
∵
∴
∴
∴
∴
∴
解得:.
综上,当时,的值为或.
故答案为:或;
②或
【知识点】等腰三角形的判定;矩形的判定与性质;翻折变换(折叠问题);相似三角形的判定与性质
【解析】【解答】(1)解:过点D作于E,如图所示,
∵,
∴,
∵,
∴,
∵,
∴,
∴四边形是矩形,
∴,,
∴,
根据勾股定理,可得.
故答案为:5;
(3)②分两种情况:
1)当点P在上时,如图所示:
由翻折可知,点C与点关于对称,
∴,,
∵,
∴,
又∵点B与点关于对称,经过点A,
∴此时,点A为重合,则,
∴,
由股定理,得,
∴,
解得:,
∴,
∴;
2)当点P在上时,过点D作于E,于F,如图所示:
由翻折可得:,,
∴点C与点关于对称,
∵,,
∴,
∴,
∴,
由(1)知:,
∴,
∴,
∵点B与点关于对称,
∴,
∵点C与点关于对称,
∴四边形与关于对称,
∴,
∴,
∴,
∵经过点A,,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
解得:,
∴,
解得:.
综上,当直线经过点A时,的值为或.
故答案为:或.
【分析】(1)过点D作于E,先证明四边形是矩形,得,,从而得出,然后由勾股定理求解;
(2)分类讨论:①当点P在上时,;②当点P在上时,,分别求解即可;
(3)①分类讨论:1)当点P在上时,2)当点P在上时,分别求解即可;
②分类讨论:1)当点P在上时,2)当点P在上时,分别求解即可.
4.方程的思想
11.
(1)如图1,在矩形中,,,点E为边上一点,沿直线将矩形折叠,使点C落在边上的点处.求的长;
(2)如图2,展开后,将沿线段向右平移,使点的对应点与点B重合,得到,与交于点F,求线段的长;
(3)在图1中,将绕点旋转至A,,E三点共线时,请直接写出的长.
【答案】(1)解:为矩形,,,
,,
;
(2)解:为平移后的图形,,,
,,
,
设长为,
,,
解得:,
,
,,
,
,
;
(3)解:将绕点旋转至A,,E三点共线,
分以下两种情况:
①当旋转到左侧时,如图所示:
作,交的延长线于点,
由(2)可知,
由旋转性质可知,,
,
,
,
四边形为矩形,
,,
,
②当旋转到右侧时,如图所示:
作,交的延长线于点,
由(2)可知,
由旋转性质可知,,
,
,
四边形为矩形,
,,
,
.
【知识点】勾股定理;矩形的性质;矩形的判定;相似三角形的判定与性质;旋转的性质
【解析】【分析】(1)根据矩形的性质、翻折的性质和勾股定理可以直接求解;
(2)根据勾股定理,可得EB的长;根据三角形相似的判定和性质,可列比例式,求出CF的长;根据线段的计算,可得EF的长;
(3)根据旋转的角度不同,进行分类讨论;根据旋转的性质,矩形的判定和性质以及勾股定理可以直接求出DC的值.
12.如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交射线BC于点E,设AP=x.
⑴当x为何值时,△APD是等腰三角形
⑵若设BE=y,求y关于x的函数关系式;
⑶若BC的长可以变化,在现在的条件下,是否存在点P,使得PQ经过点C 若存在,求出相应的AP的长;若不存在,请说明理由,并直接写出当BC的长在什么范围内时,可以存在这样的点P,使得PQ经过点C.
【答案】解:(1)过D点作DH⊥AB于H,则四边形DHBC为矩形,
∴DH=BC=4,HB=CD=6.
∴AH=2,AD=2.
∵AP=x,
∴PH=x﹣2,
情况①:当AP=AD时,即x=2.
情况②:当AD=PD时,则AH=PH.
∴2=x﹣2,解得x=4.
情况③:当AP=PD时,
则Rt△DPH中,x2=42+(x﹣2)2,解得x=5.
∵2<x<8,
∴当x为2、4、5时,△APD是等腰三角形.
(2)∵∠DPE=∠DHP=90°,
∴∠DPH+∠EPB=∠DPH+∠HDP=90°.
∴∠HDP=∠EPB.
又∵∠DHP=∠B=90°,
∴△DPH∽△PEB.
∴=,
∴=.
整理得:y=(x﹣2)(8﹣x)=﹣x2+x﹣4;
(3)存在.
设BC=a,则由(2)得△DPH∽△PEB,
∴=,
∴y=,
当y=a时,
(8﹣x)(x﹣2)=a2
x2﹣10x+(16+a2)=0,
∴△=100﹣4(16+a2),
∵△≥0,
∴100﹣64﹣4a2≥0,
4a2≤36,
又∵a>0,
∴a≤3,
∴0<a≤3,
∴满足0<BC≤3时,存在点P,使得PQ经过C.
【知识点】一元二次方程根的判别式及应用;立体图形的初步认识;相似三角形的判定与性质
【解析】【分析】(1)过D点作DH⊥AB于H,则四边形DHBC为矩形,在Rt△AHD中,由勾股定理可求得DH、AD、PH的值,若△ADP为等腰三角形,则分三种情况:①当AP=AD时,x=AP=AD,②当AD=PD时,有AH=PH,故x=AH+PH,③当AP=PD时,则在Rt△DPH中,由勾股定理可求得DP的值,有x=AP=DP.
(2)易证:△DPH∽△PEB ,即,故可求得y与x的关系式.
(3)利用△DPH∽△PEB,得出,进而利用根的判别式和一元二次不等式解集得出即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
