人教版九年级数学下名师点拨与训练第27章相似第27章 综合质量检测卷(含解析)
文档属性
| 名称 | 人教版九年级数学下名师点拨与训练第27章相似第27章 综合质量检测卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版九年级数学下名师点拨与训练
第27章 相似
第27章 综合质量检测卷
一、选择题(每小题3分,共30分)
1.若与相似且对应中线之比为,则周长之比和面积比分别是( )
A., B.,
C., D.,
2.如图,点D,E分别在△ABC的AB,AC边上,且DE∥BC,若CE∶AE=2∶3,BC=10,则DE的长为( )
A.4 B.5 C.6 D.7
3.比值为(约0.618)的比例被公认为是最能引起美感的比例,因此被称为黄金分割比,我们中国的国旗宽与长之比就非常接近这个比例,如果某面国旗长为2米,则其宽约为( )
A.1.5米 B.1.2米 C.1.0米 D.0.8米
4.如图,矩形中,,,以点为圆心,适当长为半径画弧,分别交,于点E、F,再分别以点E、F为圆心,大于长为半径画弧,两弧交于点,作射线,过点作的垂线分别交,于点M、N,则的长为( )
A. B. C. D.5
5.如图,等边中,点,分别在边,上,,交于点. 若. 则的长为( )
A. B. C. D.
6.大约在两千四五百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验(如图),解释了小孔成倒像的原理,并在《墨经》中有这样的记录:“景到,在午有端,与景长,说在端”.物理课上,小明记录了他和同桌所做的小孔成像实验数据(如图):物距为,像距为,蜡烛火焰倒立的像的高度是,则蜡烛火焰的高度是( ).
A. B. C. D.
7.如图,C是以为直径的上的一点,是的切线,,E为的中点,连接并延长交于点D,若,则的长度为( ).
A. B. C. D.2
8.如图,五边形ABCDE是由五边形FGHMN经过位似变换得到的,点O是位似中心,F、G、H、M、N分别是OA、OB、OC、OD、OE的中点,则五边形ABCDE与五边形FGHMN的面积比是( )
A.2:1 B.4:1 C.5:1 D.6:1
9.某数学兴趣小组为了估算河的宽度,在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QR=60m,则河的宽度PQ为( )
A.30m B.60m C.90m D.120m
10.有一块锐角三角形余料,边的长为,边上的高为,现要把它分割成若干个邻边长分别为和的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小长方形的长为的边在上,则按如图方式分割成的小长方形零件最多有( )
A.5个 B.6个 C.7个 D.8个
二、填空题(每小题3分,共15分)
11. 已知,则 .
12.如图,在等边中,点在BC上,,把沿直线MN对折,使点恰好落在点,则 .
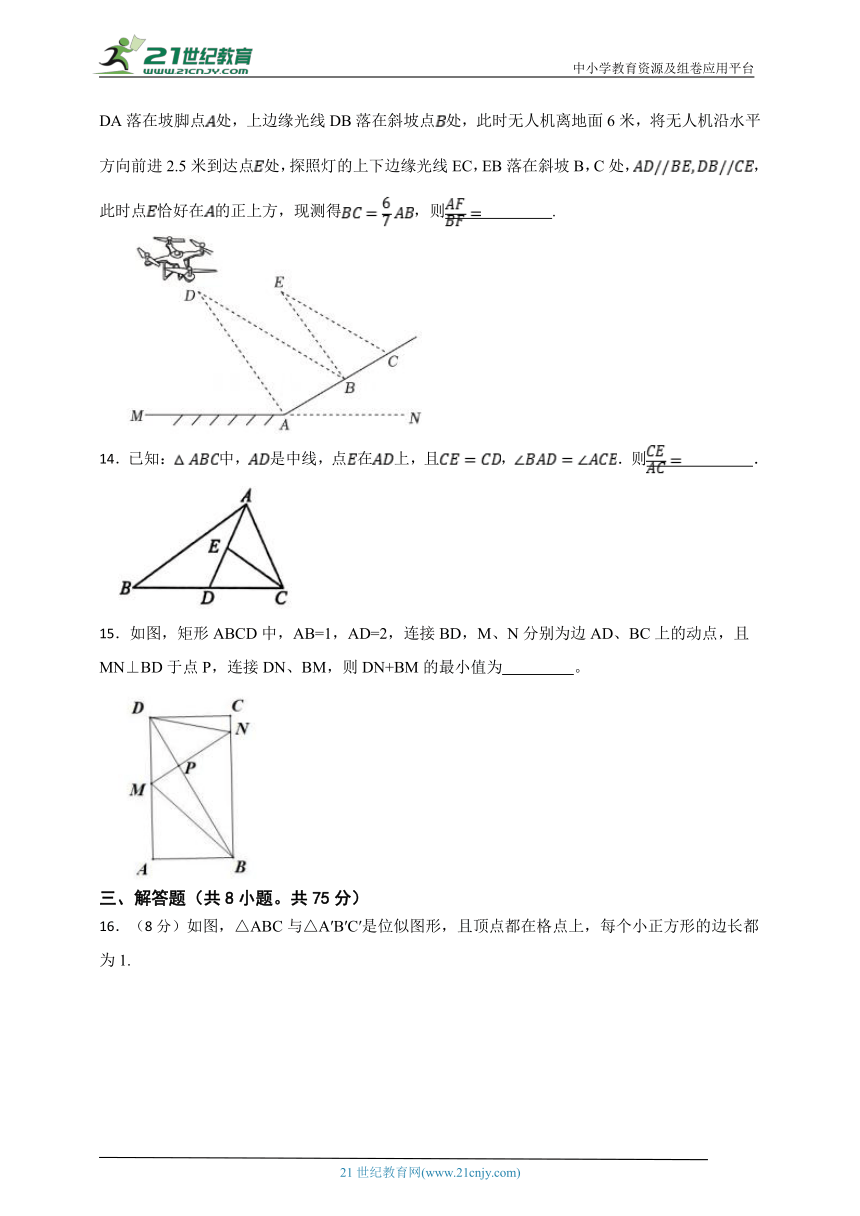
13.利用无人机探照灯测量坡面的角度.如图,一架无人机探照灯在点处,测得它的下边缘光线DA落在坡脚点处,上边缘光线DB落在斜坡点处,此时无人机离地面6米,将无人机沿水平方向前进2.5米到达点处,探照灯的上下边缘光线EC,EB落在斜坡B,C处,,此时点恰好在的正上方,现测得,则 .
14.已知:中,是中线,点在上,且,.则 .
15.如图,矩形ABCD中,AB=1,AD=2,连接BD,M、N分别为边AD、BC上的动点,且MN⊥BD于点P,连接DN、BM,则DN+BM的最小值为 。
三、解答题(共8小题。共75分)
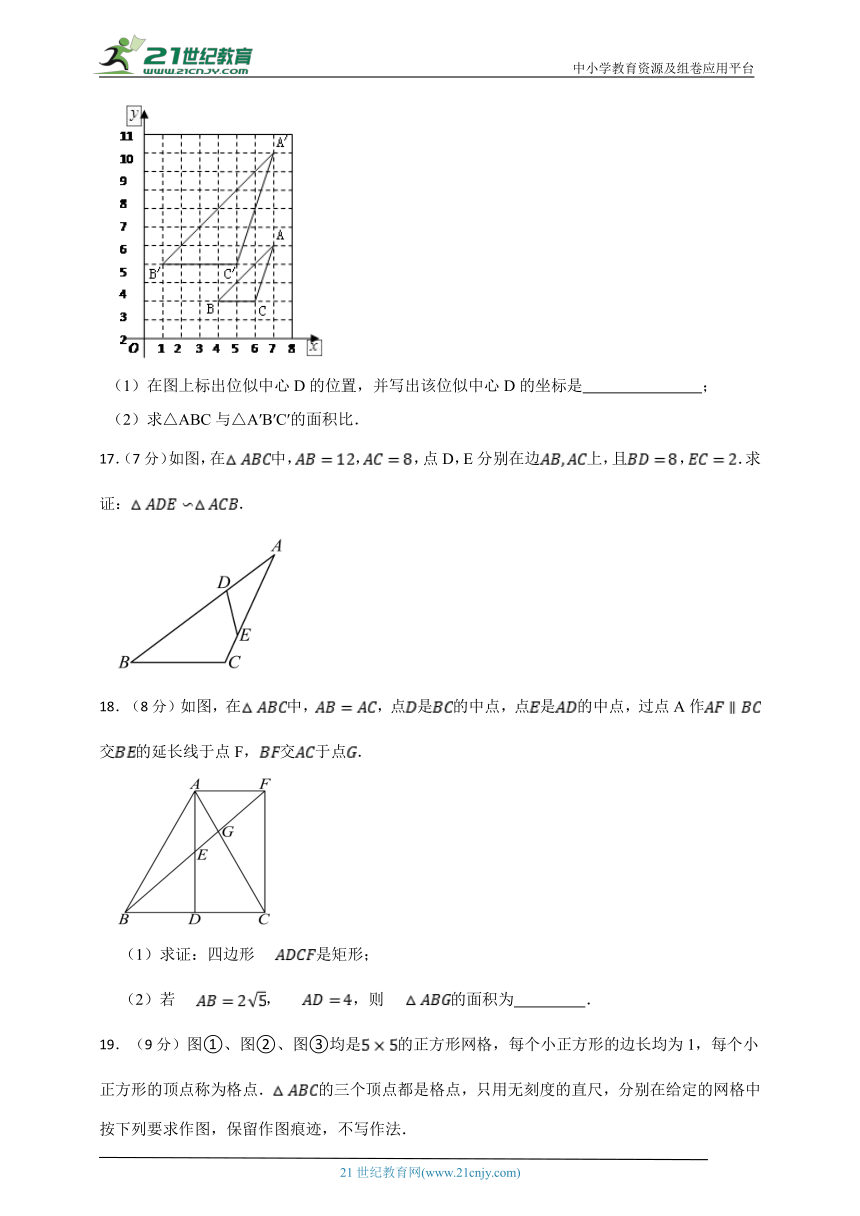
16.(8分)如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,每个小正方形的边长都为1.
(1)在图上标出位似中心D的位置,并写出该位似中心D的坐标是 ;
(2)求△ABC与△A′B′C′的面积比.
17.(7分)如图,在中,,,点D,E分别在边上,且,.求证:.
18.(8分)如图,在中,,点是的中点,点是的中点,过点A作交的延长线于点F,交于点.
(1)求证:四边形是矩形;
(2)若,,则的面积为 .
19.(9分)图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.的三个顶点都是格点,只用无刻度的直尺,分别在给定的网格中按下列要求作图,保留作图痕迹,不写作法.
(1)以点为位似中心,把缩小为原来的,得到,在图①中画出;
(2)在图②中,作出的高线;
(3)在图③中,在边上作点,使线段的长度为.
20.(9分)根据以下素材,探索解决问题.
测量旗杆的高度
素材1 可以利用影子测量旗杆的高度.如图1,光线,DN,BM分别是旗杆和小陈同学在同一时刻的影子.
素材2 可以利用镜子测量旗杆的高度.如图2,小陈同学从镜子E中刚好可以看见旗杆的顶端C,测得.
素材3 可以利用标杆测量旗杆的高度.如图3,点G,P,C在同一直线上,标杆,测得,.(说明:小陈同学、旗杆CD与标杆PQ均垂直于地面,小陈同学的眼睛G离地面的距离)
(1)任务1 利用素材1证明△ABM△CDN;
(2)任务2 在素材2中,小陈同学还要测量图中哪条线段的长度(旗杆无法直接测量),才能求出旗杆的高度?若把该线段的长度记为a,请你用含a的式子表示出旗杆的高度;
(3)任务3 利用素材3求出旗杆的高度.
21.(9分)阅读理解:
如图1,若在四边形ABCD的边AB上任取一点E(点E与点A,B不重合),分别连结ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,若∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,请直接写出的值.
图1 图2 图3
21.(12分) 小明在学习过程中,对教材的一个习题做如下探究:
(1)【习题回顾】:如图,在等边三角形ABC的AC、BC边上各取一点P,Q使AP=CQ,AQ,BP相交于点O,求∠BOQ的度数.请你解答该习题.
(2)【拓展延伸】:如图1,在等腰Rt△ABC的AC,BC边上各取一点P,Q,使AP=CQ,BP平分∠ABC, AQ=,∠BAC=90°,求BP的长.小明的思路:过点A作AG∥BC交BP延长线于点G,证明△AQC≌△GPA,
(3)如图2,在Rt△ABC的AC、BC边上各取一点P、Q,使CQ=2AP,BP平分∠ABC,,∠BAC=90°,求AQ,BP的数量关系,请你解答小明提出的问题.
22.(12分)如图,在平面直角坐标系中,抛物线:经过点和.
(1)求抛物线的对称轴.
(2)当时,将抛物线向左平移2个单位,再向下平移1个单位,得到抛物线.
①求抛物线的解析式.
②设抛物线与轴交于,两点(点在点的右侧),与轴交于点,连接.点为第一象限内抛物线上一动点,过点作于点.设点的横坐标为.是否存在点,使得以点,,为顶点的三角形与相似,若存在,求出的值;若不存在,请说明理由.
23 .(13分)小明在学习过程中,对教材的一个习题做如下探究:
(1)【习题回顾】:如图,在等边三角形ABC的AC、BC边上各取一点P,Q使AP=CQ,AQ,BP相交于点O,求∠BOQ的度数.请你解答该习题.
(2)【拓展延伸】:如图1,在等腰Rt△ABC的AC,BC边上各取一点P,Q,使AP=CQ,BP平分∠ABC, AQ=,∠BAC=90°,求BP的长.小明的思路:过点A作AG∥BC交BP延长线于点G,证明△AQC≌△GPA,
(3)如图2,在Rt△ABC的AC、BC边上各取一点P、Q,使CQ=2AP,BP平分∠ABC,,∠BAC=90°,求AQ,BP的数量关系,请你解答小明提出的问题.
人教版九年级数学下名师点拨与训练
第27章 相似
第27章 综合质量检测卷
一、选择题(每小题3分,共30分)
1.若与相似且对应中线之比为,则周长之比和面积比分别是( )
A., B.,
C., D.,
【答案】B
【知识点】相似三角形的性质
【解析】【解答】解:与相似,且对应中线之比为,
其相似比为,
与周长之比为,
与面积比为,
故答案为:B.
【分析】根据相似三角形的性质求解即可。
2.如图,点D,E分别在△ABC的AB,AC边上,且DE∥BC,若CE∶AE=2∶3,BC=10,则DE的长为( )
A.4 B.5 C.6 D.7
【答案】C
【知识点】相似三角形的判定与性质
【解析】【解答】解:∵CE∶AE=2∶3,
∴AE∶CE=3∶2,
∴AE∶(AE+CE)=3∶(3+2),
∵DE∥BC,
∴ ADE∽ ABC,
∴=,
∵BC=10,
∴=,
∴DE=6,
故答案为:C.
【分析】根据比例的性质求出AE∶AC=3∶5,根据平行于三角形一边得直线,截其它两边,所截的三角形与原三角形相似得△ADE∽△ABC,再根据相似三角形的对应边成比例建立方程,可求出DE的长.
3.比值为(约0.618)的比例被公认为是最能引起美感的比例,因此被称为黄金分割比,我们中国的国旗宽与长之比就非常接近这个比例,如果某面国旗长为2米,则其宽约为( )
A.1.5米 B.1.2米 C.1.0米 D.0.8米
【答案】B
【知识点】黄金分割
【解析】【解答】解:设国旗的宽为x米,
由题意得x∶2=0.618,
解得x≈1.2.
故答案为:B.
【分析】根据中国的国旗宽与长之比等于黄金分割比例出方程,求解即可.
4.如图,矩形中,,,以点为圆心,适当长为半径画弧,分别交,于点E、F,再分别以点E、F为圆心,大于长为半径画弧,两弧交于点,作射线,过点作的垂线分别交,于点M、N,则的长为( )
A. B. C. D.5
【答案】C
【知识点】勾股定理;矩形的性质;相似三角形的判定与性质
【解析】【解答】解:在矩形中,,,,
由勾股定理可得,
∵的平分线是BP
,
,,
,
,
,
,
,
,
,
,
∴由勾股定理可得.
故选:C.
【分析】先利用勾股定理求出,再证明,利用相似三角形的性质可得,求得,最后利用勾股定理求出的长即可.
5.如图,等边中,点,分别在边,上,,交于点. 若. 则的长为( )
A. B. C. D.
【答案】D
【知识点】等边三角形的性质;勾股定理;相似三角形的判定与性质
【解析】【解答】解:如图,过点E作EG⊥BC于点G,
,,
,
是等边三角形,
,
,,
,
,
,
,
,
,
,
,
,
,
故答案为:D.
【分析】过点E作EG⊥BC于点G,根据题意易得CE=2,由等边三角形性质得∠ABD=∠C=60°,由含30°角直角三角形性质求出CG=1,利用勾股定理算出GE、BE的长,然后利用SAS判断出△ABD≌△BCE,得∠FDB=∠CEB,结合公共角∠FBD=∠CBE,由有两组角对应相等的两个三角形相似得△FBD∽△CBE,由相似三角形对应边成比例建立方程可算出BF的长,进而根据EF=BE-BF可算出答案.
6.大约在两千四五百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验(如图),解释了小孔成倒像的原理,并在《墨经》中有这样的记录:“景到,在午有端,与景长,说在端”.物理课上,小明记录了他和同桌所做的小孔成像实验数据(如图):物距为,像距为,蜡烛火焰倒立的像的高度是,则蜡烛火焰的高度是( ).
A. B. C. D.
【答案】A
【知识点】相似三角形的应用
【解析】【解答】解:设蜡烛火焰的高度是x cm,
则有,
解得=4,
即蜡烛火焰的高度是4cm.
故答案为:A.
【分析】根据小孔成像以及相似三角形的性质可知,蜡烛火焰的高度与蜡烛火焰倒立像的高度的比值,等于物距与像距的比值.根据小孔成像以及相似三角形的性质可知,蜡烛火焰的高度与蜡烛火焰倒立像的高度的比值,等于物距与像距的比值.
7.如图,C是以为直径的上的一点,是的切线,,E为的中点,连接并延长交于点D,若,则的长度为( ).
A. B. C. D.2
【答案】C
【知识点】勾股定理;切线的性质;相似三角形的判定与性质
【解析】【解答】解:如图:连接并延长,过点D作延长线于点F,连接,
∵直径,E为的中点,
∴,
∴,
∵
∴
设,则,
∴,即,解得:,
在中,,
∴,解得:(负值已舍去),
∴,,
∴在中,,
又∵是的切线,,
∴,
在中,
∴.
故选:C.
【分析】连接OC并延长,过点D作DF⊥OC延长线于点F,连接OD,由PC∥AB,证,设OF=x,则CF=x+2,然后利用相似三角形的性质,结合切线的性质和勾股定理求得求解即可.
8.如图,五边形ABCDE是由五边形FGHMN经过位似变换得到的,点O是位似中心,F、G、H、M、N分别是OA、OB、OC、OD、OE的中点,则五边形ABCDE与五边形FGHMN的面积比是( )
A.2:1 B.4:1 C.5:1 D.6:1
【答案】B
【知识点】相似多边形;位似变换
【解析】【解答】解:∵F为AO的中点,
∴OF:OA=1:2,
∵ 五边形ABCDE是由五边形FGHMN经过位似变换得到的 ,
∴FN∥AE,
∴△OFN∽△OAE,
∴OF∶OA=FN∶AE=1∶2
∴五边形ABCDE与五边形FGHMN的面积比为:4:1.
故答案为:B.
【分析】由五边形ABCDE与五边形FGHMN关于点O成位似关系,且OF:OA=1:2,可得位似比为1:2,根据形似图形的面积比等于相似比的平方,即可求得答案.
9.某数学兴趣小组为了估算河的宽度,在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QR=60m,则河的宽度PQ为( )
A.30m B.60m C.90m D.120m
【答案】C
【知识点】相似三角形的应用
【解析】【解答】解:根据题意得QR∥ST,
∴△PQR∽△PST
∴,即,
解得:PQ=90m
故答案为:C.
【分析】根据相似三角形的性质得出,代数计算求解即可.
10.有一块锐角三角形余料,边的长为,边上的高为,现要把它分割成若干个邻边长分别为和的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小长方形的长为的边在上,则按如图方式分割成的小长方形零件最多有( )
A.5个 B.6个 C.7个 D.8个
【答案】B
【知识点】矩形的性质;相似三角形的应用
【解析】【解答】解:如图:当最上层的小长方形的一边与交于点E、F时,,于,交于,
∴,
∴,即,
解得,,
∴,
∵小长方形的宽为
∴能分割三层小长方形,且最上一层正好能分割一个小长方形,
设第二层靠近点A的边为x,
根据三角形相似可得:,
解得,即第二层正好能分割两个小长方形,
设最下层靠近点A的边为,
根据三角形相似可得:,
解得,即最下层正好能分割三个小长方形,
∴按如图方式分割成的小长方形零件最多有个,
故答案为:B.
【分析】 当最上层的小长方形的一边与AB、AC交于点E、F时,EF∥BC,AD⊥BC于D,交EF于G,则△AEF∽△ABC,由相似三角形对应边成比例建立方程可求出AG的长,然后根据DG=AD-AG可求出DG的长, 所以△ABC能分割三层小长方形,且最上一层正好能分割一个小长方形,设第二层靠近点A的边为x,根据相似三角形对应边成比例建立方程求出x=10,即第二层正好能分割两个小长方形,设最下层靠近点A的边为y,根据相似三角形对应边成比例建立方程求出y=15,即最下层正好能分割三个小长方形,从而即可得出答案.
二、填空题(每小题3分,共15分)
11. 已知,则 .
【答案】
【知识点】比例的性质
【解析】【解答】解:∵设,
∴a=3k,b=4k,
∴.
故答案为:.
【分析】根据等比的性质,设,则a=3k,b=4k,然后代入待求式子,合并后约分化简即可.
12.如图,在等边中,点在BC上,,把沿直线MN对折,使点恰好落在点,则 .
【答案】
【知识点】等边三角形的性质;轴对称的性质;相似三角形的判定与性质
【解析】【解答】解:∵BD:DC=2:3,
∴设BD=2a,则CD=3a,BC=5a.
∵△ABC是等边三角形,
∴AB=BC=AC=5a,∠ABC=∠ACB=∠BAC=60°,
由折叠的性质可知:MN是线段AD的垂直平分线,
∴AM=DM,AN=DN,
∴BM+MD+BD=7a,DN+NC+DC=8a,
∵∠MDN=∠BAC=∠ABC=60°,
∴∠NDC+∠MDB=∠BMD+∠MDB=120°,
∴∠NDC=∠BMD,
∵∠ABC=∠ACB=60°,
∴△BMD∽△CDN,
∴(BM+MD+BD):(DN+NC+CD)=MD:DN=AM:AN,
即AM:AN=7:8,
故答案为: .
【分析】设BD=2a,则CD=3a,根据折叠的性质可得AM=DM,AN=DN,根据等边三角形的性质准备条件,证△BMD∽△CDN,根据相似三角形周长的性质求解即可。
13.利用无人机探照灯测量坡面的角度.如图,一架无人机探照灯在点处,测得它的下边缘光线DA落在坡脚点处,上边缘光线DB落在斜坡点处,此时无人机离地面6米,将无人机沿水平方向前进2.5米到达点处,探照灯的上下边缘光线EC,EB落在斜坡B,C处,,此时点恰好在的正上方,现测得,则 .
【答案】
【知识点】相似三角形的应用;锐角三角函数的定义
【解析】【解答】解:如图,连接,作于,
点恰好在的正上方,
是直角三角形,
又,,
根据勾股定理得,
,
∵ ,
,,
,
,
又∵,
,
,
,
,
,,
,
,
,
,
,
故答案为:.
【分析】通过做辅助线,构造直角,根据勾股定理求出的长,易证,依据相似的性质得出,求出BE,作于,由,列比例解出和,进而求出,根据,,进而求出
14.已知:中,是中线,点在上,且,.则 .
【答案】
【知识点】三角形的外角性质;等腰三角形的判定与性质;相似三角形的判定与性质
【解析】【解答】解:是边上的中线,
.
,
.
.
,
.
又,
.
.
.
.
.
故答案为:
【分析】本题考查相似三角形的判定与性质、等腰三角形的性质、三角形外角与内角的关系.先利用等腰三角形的性质,三角形外角与内角的关系可推出,再根据已知条件可证明,利用相似三角形的性质可得:,化简可用表示出,再代入比例式可求出答案.
15.如图,矩形ABCD中,AB=1,AD=2,连接BD,M、N分别为边AD、BC上的动点,且MN⊥BD于点P,连接DN、BM,则DN+BM的最小值为 。
【答案】
【知识点】平行四边形的性质;相似三角形的判定与性质;将军饮马模型-一线两点(一动两定)
【解析】【解答】解:如图,过点M作ME⊥BC,垂足为点E,
∵四边形ABCD是矩形,
∴∠A=∠ABC=∠BCD=∠CDA=90°,
∴四边形ABEM和四边形CDME均为矩形,
∴ME=AB=1,∠MPD+∠PDM=90°,
又∵MN⊥BD,
∴∠EMN+∠MPD=90°,
∴∠EMN=∠ADB,
∴在Rt△BAD和Rt△NEM中,
,
∴,解得:NE=,
以MN和BM作为平行四边形的两边向右侧构造平行四边形MBGN,过点G作HF⊥AB交AB延长线于点F,交DC延长线于点H,
由同角余角相等,即同理可证∠FBG=∠ADB,四边形BFHC为矩形,
∴BG=MN,NG=BM,FH=BC,BF=CH,
又∵BG=MN,∠F=∠MEN=90°,
∴△BFH≌△MEN(AAS),
∴CH=BF=ME=1,FG=NE=,HG=HF-FG=BC-FG=,
在Rt△DHG中,DG=,
又∵ DN+BM=DN+NG≥DG,
当且仅当D、N、G三点共线时,.
故答案为:.
【分析】利用MN⊥BD先分析边角关系,构造相似或利用同角三角函数值,即分析得MN为定长,故目标线段最值为“造桥选址”最值问题,即构造平行四边形的性质进行线段转移,将双动点转换为单动点的“将军饮马”线段和最值,利用勾股定理构造直角解之即可.
三、解答题(共8小题。共75分)
16.(8分)如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,每个小正方形的边长都为1.
(1)在图上标出位似中心D的位置,并写出该位似中心D的坐标是 ;
(2)求△ABC与△A′B′C′的面积比.
【答案】解:(1)如图:D(7,0);
(2)∵△ABC∽△A′B′C′
∴
【知识点】相似三角形的性质;作图﹣位似变换
【解析】【分析】考查位似.
17.(7分)如图,在中,,,点D,E分别在边上,且,.求证:.
【答案】【解答】
解:∵,,,,∴,,
∴,,
∴,
又∵,
∴.
【知识点】相似三角形的判定
【解析】【分析】首先求出,的长,再求出,又因为,根据相似三角形的判定可证得
18.(8分)如图,在中,,点是的中点,点是的中点,过点A作交的延长线于点F,交于点.
(1)求证:四边形是矩形;
(2)若,,则的面积为 .
【答案】(1)证明:,
,
∵点E是的中点,
,
在和中,
,
;
,点是线段的中点,
,,
,AF=CD,
四边形是矩形;
(2)
【知识点】等腰三角形的性质;矩形的判定;相似三角形的判定与性质
【解析】【解答】(2)解:根据(1)得,∴根据勾股定理可得,
,,
,
,
,
,
,
.
故答案为:.
【分析】(1)由二直线平行,内错角相等可得∠AFE=∠DBE,由中点定义可得AE=DE,从而可用“AAS”证出△BDE≌△FAE,由全等三角形的对应边相等可得AF=BD,再根据等腰三角形的三线合一可得AD⊥BC,BD=CD,则AF=CD,从而即可得到平行四边形ADCF是矩形;
(2)在Rt△ABD中,用勾股定理求得BD的长,从而求得AF=BD=2,BC=2BD=4,根据三角形面积公式算出△ABC的面积;由平行于三角形一边得直线,截其它两边的延长线,所截的三角形与原三角形相似得△AGF∽△CGB,利用相似三角形的对应边成比例得到,然后格局同高三角形的面积之比等于对应底之比可得,最后由求解即可.
19.(9分)图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.的三个顶点都是格点,只用无刻度的直尺,分别在给定的网格中按下列要求作图,保留作图痕迹,不写作法.
(1)以点为位似中心,把缩小为原来的,得到,在图①中画出;
(2)在图②中,作出的高线;
(3)在图③中,在边上作点,使线段的长度为.
【答案】(1)见详解
(2)见详解
(3)见详解
【知识点】三角形的角平分线、中线和高;勾股定理;作图﹣位似变换
【解析】【解答】(1)如图所示:即为所求;
(2)如图所示,即为所求;
(3)如图所示:点即为所求.
【分析】(1)根据题意再结合网格,找到、中点,然后相连接,即可得到答案;
(2)根据题意再结合网格,利用直角三角形中两锐角互余的性质,即可得到答案;
(3)根据题意再结合网格,求出的长度为,,即,找到的五等分点,即可得到答案.
20.(9分)根据以下素材,探索解决问题.
测量旗杆的高度
素材1 可以利用影子测量旗杆的高度.如图1,光线,DN,BM分别是旗杆和小陈同学在同一时刻的影子.
素材2 可以利用镜子测量旗杆的高度.如图2,小陈同学从镜子E中刚好可以看见旗杆的顶端C,测得.
素材3 可以利用标杆测量旗杆的高度.如图3,点G,P,C在同一直线上,标杆,测得,.(说明:小陈同学、旗杆CD与标杆PQ均垂直于地面,小陈同学的眼睛G离地面的距离)
(1)任务1 利用素材1证明△ABM△CDN;
(2)任务2 在素材2中,小陈同学还要测量图中哪条线段的长度(旗杆无法直接测量),才能求出旗杆的高度?若把该线段的长度记为a,请你用含a的式子表示出旗杆的高度;
(3)任务3 利用素材3求出旗杆的高度.
【答案】(1)证明:由题意知:,,
即,
∵,
∴,
∴.
(2)解:小陈同学还要测量图中线段DE的长度,记为a.
由题意知:,
∵,,
∴,
∴.
∴,
∵,,,
∴.
(3)解:过点G作于点H,交PQ于点F.
由题意知:,,,
即,
,,
∵,,
∴,
∴,
∴,
∴,
∴,
∴.
【知识点】相似三角形的应用
【解析】【分析】(1)由题意得到:,然后根据平行线的性质得到:,进而即可求证;
(2)把线段DE的长度记为a,由题意得到:,进而证明,得到:,进而可得到CD的长;
(3)过点G作于点H,交PQ于点F,由题意得到:,,,进而求出PF的长度,然后根据垂直的定义和平行线的性质即可证明,得到:,进而即可求出CD的长.
21.(9分)阅读理解:
如图1,若在四边形ABCD的边AB上任取一点E(点E与点A,B不重合),分别连结ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,若∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,请直接写出的值.
图1 图2 图3
【答案】解:(1)点E是四边形ABCD的边AB上的相似点.
理由:∵∠A=55°,
∴∠ADE+∠DEA=125°.
∵∠DEC=55°,
∴∠BEC+∠DEA=125°.
∴∠ADE=∠BEC.
∵∠A=∠B,
∴△ADE∽△BEC.
∴点E是四边形ABCD的AB边上的相似点
(2)作图如下:
图1图2
(3).
【知识点】矩形的性质;梯形;相似三角形的判定与性质
【解析】【分析】(1)要证明点E是四边形ABCD的边AB上的相似点,只要证明有一组三角形相似就行,很容易证明△ADE∽△BEC,所以问题得解.
(2)根据两个直角三角形相似得到强相似点的两种情况即可.
(3)因为点E是梯形ABCD的边AB上的一个强相似点,所以就有相似三角形出现,根据相似三角形的对应线段成比例,可以判断出BC和AB的数量关系,从而可求出解.
21.(12分) 小明在学习过程中,对教材的一个习题做如下探究:
(1)【习题回顾】:如图,在等边三角形ABC的AC、BC边上各取一点P,Q使AP=CQ,AQ,BP相交于点O,求∠BOQ的度数.请你解答该习题.
(2)【拓展延伸】:如图1,在等腰Rt△ABC的AC,BC边上各取一点P,Q,使AP=CQ,BP平分∠ABC, AQ=,∠BAC=90°,求BP的长.小明的思路:过点A作AG∥BC交BP延长线于点G,证明△AQC≌△GPA,
(3)如图2,在Rt△ABC的AC、BC边上各取一点P、Q,使CQ=2AP,BP平分∠ABC,,∠BAC=90°,求AQ,BP的数量关系,请你解答小明提出的问题.
【答案】(1)解:在等边△ABC中,AB=AC,∠BAP=∠C=60°,AP=CQ,
∴△ABP≌△CAQ(SAS),
∴∠ABP=∠CAQ.
∵∠BOQ=∠BAO+∠ABP,
∴∠BOQ=∠BAO+∠CAQ=∠BAC=60°;
(2)解:过点A作AG∥BC交BP的延长线于点G,
∴∠PAG=∠C,∠PBC=∠G,
∵BP平分∠ABC,
∴∠PBC=∠ABP,
∴∠G=∠ABP,
∴AG=AB,
∵AC=AB,
∴AG=AC,
∵AP=CQ,
∴△CAQ≌△AGP(SAS),
∴PG=AQ=.
∵AG∥BC,
∴△APG∽△CPB,
∴,
而,
∴,
∴,
∵PG=,
∴BP=2;
(3)解:如图2,过点A作AG∥BC交BP的延长线于点G,
由(1)知∠PAG=∠C,AG=AB,
∵,
∴,
∵CQ=2AP,
∴,
∴△APG∽△CQA,
∴,
∴,
Rt△ABC中,,
∴,
∴,
∵AG∥BC,
∴△APG∽△CPB,
∴,
∴,
∴,
∴2BP=AQ.
【知识点】角平分线的性质;相似三角形的判定与性质;三角形全等的判定-SAS
【解析】【分析】(1)根据三角形全等的判定(SAS)和性质,可得∠ABP=∠CAQ;根据交的计算,即可求出∠BOQ的度数;
(2)根据角平分线的性质,可得∠PBC=∠ABP;根据三角形全等的判定(SAS)和性质,可得PG=AQ;根据三角形相似的判定和性质,可列比例式,进而求出BP的值;
(3)根据三角形相似的判定和性质,可列比例式,得到,,进而可得AQ和BP的数量关系.
22.(12分)如图,在平面直角坐标系中,抛物线:经过点和.
(1)求抛物线的对称轴.
(2)当时,将抛物线向左平移2个单位,再向下平移1个单位,得到抛物线.
①求抛物线的解析式.
②设抛物线与轴交于,两点(点在点的右侧),与轴交于点,连接.点为第一象限内抛物线上一动点,过点作于点.设点的横坐标为.是否存在点,使得以点,,为顶点的三角形与相似,若存在,求出的值;若不存在,请说明理由.
【答案】(1)x=2.5;(2)①;②1或
【分析】(1)根据函数图像所过的点的特点结合函数性质,可知两点中点横坐标即为对称轴;
(2)①根据平移可得已知点平移后点的坐标,平移过程中a的值不发生改变,所以利用交点式可以求出函数解析式;
②根据条件求出A、B、C、D四点的坐标,由条件可知三角形相似有两种情况,分别讨论两种情况,根据相似的性质可求出m的值.
【详解】解:(1)因为抛物线图像过(1,1)、(4,1)两点,
这两点的纵坐标相同,根据抛物线的性质可知,对称轴是x=(1+4)÷2=2.5,;
(2)①将点(1,1)、(4,1)向左平移2个单位,再向下平移1个单位,得到(-1,0),(2,0),将点(-1,0),(2,0),a=-1,
根据交点式可求出C1二次函数表达式为;
②根据①中的函数关系式,可得A(2,0),B(-1,0),C(0,2),D(m,),且m>0
由图像可知∠BOC=∠DEO=90°,
则以点,,为顶点的三角形与相似有两种情况,
(i)当△ODE∽△BCO时,
则,即,
解得m=1或-2(舍),
(ii)当△ODE∽△CBO时,
则,即,
解得
所以满足条件的m的值为1或.
【点睛】本题主要考查了一元二次函数图形的平移、表达式求法、相似三角形等知识点,熟练运用数形结合是解决问题的关键.
23 .(13分)小明在学习过程中,对教材的一个习题做如下探究:
(1)【习题回顾】:如图,在等边三角形ABC的AC、BC边上各取一点P,Q使AP=CQ,AQ,BP相交于点O,求∠BOQ的度数.请你解答该习题.
(2)【拓展延伸】:如图1,在等腰Rt△ABC的AC,BC边上各取一点P,Q,使AP=CQ,BP平分∠ABC, AQ=,∠BAC=90°,求BP的长.小明的思路:过点A作AG∥BC交BP延长线于点G,证明△AQC≌△GPA,
(3)如图2,在Rt△ABC的AC、BC边上各取一点P、Q,使CQ=2AP,BP平分∠ABC,,∠BAC=90°,求AQ,BP的数量关系,请你解答小明提出的问题.
【答案】(1)解:在等边△ABC中,AB=AC,∠BAP=∠C=60°,AP=CQ,
∴△ABP≌△CAQ(SAS),
∴∠ABP=∠CAQ.
∵∠BOQ=∠BAO+∠ABP,
∴∠BOQ=∠BAO+∠CAQ=∠BAC=60°;
(2)解:过点A作AG∥BC交BP的延长线于点G,
∴∠PAG=∠C,∠PBC=∠G,
∵BP平分∠ABC,
∴∠PBC=∠ABP,
∴∠G=∠ABP,
∴AG=AB,
∵AC=AB,
∴AG=AC,
∵AP=CQ,
∴△CAQ≌△AGP(SAS),
∴PG=AQ=.
∵AG∥BC,
∴△APG∽△CPB,
∴,
而,
∴,
∴,
∵PG=,
∴BP=2;
(3)解:如图2,过点A作AG∥BC交BP的延长线于点G,
由(1)知∠PAG=∠C,AG=AB,
∵,
∴,
∵CQ=2AP,
∴,
∴△APG∽△CQA,
∴,
∴,
Rt△ABC中,,
∴,
∴,
∵AG∥BC,
∴△APG∽△CPB,
∴,
∴,
∴,
∴2BP=AQ.
【知识点】角平分线的性质;相似三角形的判定与性质;三角形全等的判定-SAS
【解析】【分析】(1)根据三角形全等的判定(SAS)和性质,可得∠ABP=∠CAQ;根据交的计算,即可求出∠BOQ的度数;
(2)根据角平分线的性质,可得∠PBC=∠ABP;根据三角形全等的判定(SAS)和性质,可得PG=AQ;根据三角形相似的判定和性质,可列比例式,进而求出BP的值;
(3)根据三角形相似的判定和性质,可列比例式,得到,,进而可得AQ和BP的数量关系.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级数学下名师点拨与训练
第27章 相似
第27章 综合质量检测卷
一、选择题(每小题3分,共30分)
1.若与相似且对应中线之比为,则周长之比和面积比分别是( )
A., B.,
C., D.,
2.如图,点D,E分别在△ABC的AB,AC边上,且DE∥BC,若CE∶AE=2∶3,BC=10,则DE的长为( )
A.4 B.5 C.6 D.7
3.比值为(约0.618)的比例被公认为是最能引起美感的比例,因此被称为黄金分割比,我们中国的国旗宽与长之比就非常接近这个比例,如果某面国旗长为2米,则其宽约为( )
A.1.5米 B.1.2米 C.1.0米 D.0.8米
4.如图,矩形中,,,以点为圆心,适当长为半径画弧,分别交,于点E、F,再分别以点E、F为圆心,大于长为半径画弧,两弧交于点,作射线,过点作的垂线分别交,于点M、N,则的长为( )
A. B. C. D.5
5.如图,等边中,点,分别在边,上,,交于点. 若. 则的长为( )
A. B. C. D.
6.大约在两千四五百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验(如图),解释了小孔成倒像的原理,并在《墨经》中有这样的记录:“景到,在午有端,与景长,说在端”.物理课上,小明记录了他和同桌所做的小孔成像实验数据(如图):物距为,像距为,蜡烛火焰倒立的像的高度是,则蜡烛火焰的高度是( ).
A. B. C. D.
7.如图,C是以为直径的上的一点,是的切线,,E为的中点,连接并延长交于点D,若,则的长度为( ).
A. B. C. D.2
8.如图,五边形ABCDE是由五边形FGHMN经过位似变换得到的,点O是位似中心,F、G、H、M、N分别是OA、OB、OC、OD、OE的中点,则五边形ABCDE与五边形FGHMN的面积比是( )
A.2:1 B.4:1 C.5:1 D.6:1
9.某数学兴趣小组为了估算河的宽度,在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QR=60m,则河的宽度PQ为( )
A.30m B.60m C.90m D.120m
10.有一块锐角三角形余料,边的长为,边上的高为,现要把它分割成若干个邻边长分别为和的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小长方形的长为的边在上,则按如图方式分割成的小长方形零件最多有( )
A.5个 B.6个 C.7个 D.8个
二、填空题(每小题3分,共15分)
11. 已知,则 .
12.如图,在等边中,点在BC上,,把沿直线MN对折,使点恰好落在点,则 .
13.利用无人机探照灯测量坡面的角度.如图,一架无人机探照灯在点处,测得它的下边缘光线DA落在坡脚点处,上边缘光线DB落在斜坡点处,此时无人机离地面6米,将无人机沿水平方向前进2.5米到达点处,探照灯的上下边缘光线EC,EB落在斜坡B,C处,,此时点恰好在的正上方,现测得,则 .
14.已知:中,是中线,点在上,且,.则 .
15.如图,矩形ABCD中,AB=1,AD=2,连接BD,M、N分别为边AD、BC上的动点,且MN⊥BD于点P,连接DN、BM,则DN+BM的最小值为 。
三、解答题(共8小题。共75分)
16.(8分)如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,每个小正方形的边长都为1.
(1)在图上标出位似中心D的位置,并写出该位似中心D的坐标是 ;
(2)求△ABC与△A′B′C′的面积比.
17.(7分)如图,在中,,,点D,E分别在边上,且,.求证:.
18.(8分)如图,在中,,点是的中点,点是的中点,过点A作交的延长线于点F,交于点.
(1)求证:四边形是矩形;
(2)若,,则的面积为 .
19.(9分)图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.的三个顶点都是格点,只用无刻度的直尺,分别在给定的网格中按下列要求作图,保留作图痕迹,不写作法.
(1)以点为位似中心,把缩小为原来的,得到,在图①中画出;
(2)在图②中,作出的高线;
(3)在图③中,在边上作点,使线段的长度为.
20.(9分)根据以下素材,探索解决问题.
测量旗杆的高度
素材1 可以利用影子测量旗杆的高度.如图1,光线,DN,BM分别是旗杆和小陈同学在同一时刻的影子.
素材2 可以利用镜子测量旗杆的高度.如图2,小陈同学从镜子E中刚好可以看见旗杆的顶端C,测得.
素材3 可以利用标杆测量旗杆的高度.如图3,点G,P,C在同一直线上,标杆,测得,.(说明:小陈同学、旗杆CD与标杆PQ均垂直于地面,小陈同学的眼睛G离地面的距离)
(1)任务1 利用素材1证明△ABM△CDN;
(2)任务2 在素材2中,小陈同学还要测量图中哪条线段的长度(旗杆无法直接测量),才能求出旗杆的高度?若把该线段的长度记为a,请你用含a的式子表示出旗杆的高度;
(3)任务3 利用素材3求出旗杆的高度.
21.(9分)阅读理解:
如图1,若在四边形ABCD的边AB上任取一点E(点E与点A,B不重合),分别连结ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,若∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,请直接写出的值.
图1 图2 图3
21.(12分) 小明在学习过程中,对教材的一个习题做如下探究:
(1)【习题回顾】:如图,在等边三角形ABC的AC、BC边上各取一点P,Q使AP=CQ,AQ,BP相交于点O,求∠BOQ的度数.请你解答该习题.
(2)【拓展延伸】:如图1,在等腰Rt△ABC的AC,BC边上各取一点P,Q,使AP=CQ,BP平分∠ABC, AQ=,∠BAC=90°,求BP的长.小明的思路:过点A作AG∥BC交BP延长线于点G,证明△AQC≌△GPA,
(3)如图2,在Rt△ABC的AC、BC边上各取一点P、Q,使CQ=2AP,BP平分∠ABC,,∠BAC=90°,求AQ,BP的数量关系,请你解答小明提出的问题.
22.(12分)如图,在平面直角坐标系中,抛物线:经过点和.
(1)求抛物线的对称轴.
(2)当时,将抛物线向左平移2个单位,再向下平移1个单位,得到抛物线.
①求抛物线的解析式.
②设抛物线与轴交于,两点(点在点的右侧),与轴交于点,连接.点为第一象限内抛物线上一动点,过点作于点.设点的横坐标为.是否存在点,使得以点,,为顶点的三角形与相似,若存在,求出的值;若不存在,请说明理由.
23 .(13分)小明在学习过程中,对教材的一个习题做如下探究:
(1)【习题回顾】:如图,在等边三角形ABC的AC、BC边上各取一点P,Q使AP=CQ,AQ,BP相交于点O,求∠BOQ的度数.请你解答该习题.
(2)【拓展延伸】:如图1,在等腰Rt△ABC的AC,BC边上各取一点P,Q,使AP=CQ,BP平分∠ABC, AQ=,∠BAC=90°,求BP的长.小明的思路:过点A作AG∥BC交BP延长线于点G,证明△AQC≌△GPA,
(3)如图2,在Rt△ABC的AC、BC边上各取一点P、Q,使CQ=2AP,BP平分∠ABC,,∠BAC=90°,求AQ,BP的数量关系,请你解答小明提出的问题.
人教版九年级数学下名师点拨与训练
第27章 相似
第27章 综合质量检测卷
一、选择题(每小题3分,共30分)
1.若与相似且对应中线之比为,则周长之比和面积比分别是( )
A., B.,
C., D.,
【答案】B
【知识点】相似三角形的性质
【解析】【解答】解:与相似,且对应中线之比为,
其相似比为,
与周长之比为,
与面积比为,
故答案为:B.
【分析】根据相似三角形的性质求解即可。
2.如图,点D,E分别在△ABC的AB,AC边上,且DE∥BC,若CE∶AE=2∶3,BC=10,则DE的长为( )
A.4 B.5 C.6 D.7
【答案】C
【知识点】相似三角形的判定与性质
【解析】【解答】解:∵CE∶AE=2∶3,
∴AE∶CE=3∶2,
∴AE∶(AE+CE)=3∶(3+2),
∵DE∥BC,
∴ ADE∽ ABC,
∴=,
∵BC=10,
∴=,
∴DE=6,
故答案为:C.
【分析】根据比例的性质求出AE∶AC=3∶5,根据平行于三角形一边得直线,截其它两边,所截的三角形与原三角形相似得△ADE∽△ABC,再根据相似三角形的对应边成比例建立方程,可求出DE的长.
3.比值为(约0.618)的比例被公认为是最能引起美感的比例,因此被称为黄金分割比,我们中国的国旗宽与长之比就非常接近这个比例,如果某面国旗长为2米,则其宽约为( )
A.1.5米 B.1.2米 C.1.0米 D.0.8米
【答案】B
【知识点】黄金分割
【解析】【解答】解:设国旗的宽为x米,
由题意得x∶2=0.618,
解得x≈1.2.
故答案为:B.
【分析】根据中国的国旗宽与长之比等于黄金分割比例出方程,求解即可.
4.如图,矩形中,,,以点为圆心,适当长为半径画弧,分别交,于点E、F,再分别以点E、F为圆心,大于长为半径画弧,两弧交于点,作射线,过点作的垂线分别交,于点M、N,则的长为( )
A. B. C. D.5
【答案】C
【知识点】勾股定理;矩形的性质;相似三角形的判定与性质
【解析】【解答】解:在矩形中,,,,
由勾股定理可得,
∵的平分线是BP
,
,,
,
,
,
,
,
,
,
,
∴由勾股定理可得.
故选:C.
【分析】先利用勾股定理求出,再证明,利用相似三角形的性质可得,求得,最后利用勾股定理求出的长即可.
5.如图,等边中,点,分别在边,上,,交于点. 若. 则的长为( )
A. B. C. D.
【答案】D
【知识点】等边三角形的性质;勾股定理;相似三角形的判定与性质
【解析】【解答】解:如图,过点E作EG⊥BC于点G,
,,
,
是等边三角形,
,
,,
,
,
,
,
,
,
,
,
,
,
故答案为:D.
【分析】过点E作EG⊥BC于点G,根据题意易得CE=2,由等边三角形性质得∠ABD=∠C=60°,由含30°角直角三角形性质求出CG=1,利用勾股定理算出GE、BE的长,然后利用SAS判断出△ABD≌△BCE,得∠FDB=∠CEB,结合公共角∠FBD=∠CBE,由有两组角对应相等的两个三角形相似得△FBD∽△CBE,由相似三角形对应边成比例建立方程可算出BF的长,进而根据EF=BE-BF可算出答案.
6.大约在两千四五百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验(如图),解释了小孔成倒像的原理,并在《墨经》中有这样的记录:“景到,在午有端,与景长,说在端”.物理课上,小明记录了他和同桌所做的小孔成像实验数据(如图):物距为,像距为,蜡烛火焰倒立的像的高度是,则蜡烛火焰的高度是( ).
A. B. C. D.
【答案】A
【知识点】相似三角形的应用
【解析】【解答】解:设蜡烛火焰的高度是x cm,
则有,
解得=4,
即蜡烛火焰的高度是4cm.
故答案为:A.
【分析】根据小孔成像以及相似三角形的性质可知,蜡烛火焰的高度与蜡烛火焰倒立像的高度的比值,等于物距与像距的比值.根据小孔成像以及相似三角形的性质可知,蜡烛火焰的高度与蜡烛火焰倒立像的高度的比值,等于物距与像距的比值.
7.如图,C是以为直径的上的一点,是的切线,,E为的中点,连接并延长交于点D,若,则的长度为( ).
A. B. C. D.2
【答案】C
【知识点】勾股定理;切线的性质;相似三角形的判定与性质
【解析】【解答】解:如图:连接并延长,过点D作延长线于点F,连接,
∵直径,E为的中点,
∴,
∴,
∵
∴
设,则,
∴,即,解得:,
在中,,
∴,解得:(负值已舍去),
∴,,
∴在中,,
又∵是的切线,,
∴,
在中,
∴.
故选:C.
【分析】连接OC并延长,过点D作DF⊥OC延长线于点F,连接OD,由PC∥AB,证,设OF=x,则CF=x+2,然后利用相似三角形的性质,结合切线的性质和勾股定理求得求解即可.
8.如图,五边形ABCDE是由五边形FGHMN经过位似变换得到的,点O是位似中心,F、G、H、M、N分别是OA、OB、OC、OD、OE的中点,则五边形ABCDE与五边形FGHMN的面积比是( )
A.2:1 B.4:1 C.5:1 D.6:1
【答案】B
【知识点】相似多边形;位似变换
【解析】【解答】解:∵F为AO的中点,
∴OF:OA=1:2,
∵ 五边形ABCDE是由五边形FGHMN经过位似变换得到的 ,
∴FN∥AE,
∴△OFN∽△OAE,
∴OF∶OA=FN∶AE=1∶2
∴五边形ABCDE与五边形FGHMN的面积比为:4:1.
故答案为:B.
【分析】由五边形ABCDE与五边形FGHMN关于点O成位似关系,且OF:OA=1:2,可得位似比为1:2,根据形似图形的面积比等于相似比的平方,即可求得答案.
9.某数学兴趣小组为了估算河的宽度,在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QR=60m,则河的宽度PQ为( )
A.30m B.60m C.90m D.120m
【答案】C
【知识点】相似三角形的应用
【解析】【解答】解:根据题意得QR∥ST,
∴△PQR∽△PST
∴,即,
解得:PQ=90m
故答案为:C.
【分析】根据相似三角形的性质得出,代数计算求解即可.
10.有一块锐角三角形余料,边的长为,边上的高为,现要把它分割成若干个邻边长分别为和的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小长方形的长为的边在上,则按如图方式分割成的小长方形零件最多有( )
A.5个 B.6个 C.7个 D.8个
【答案】B
【知识点】矩形的性质;相似三角形的应用
【解析】【解答】解:如图:当最上层的小长方形的一边与交于点E、F时,,于,交于,
∴,
∴,即,
解得,,
∴,
∵小长方形的宽为
∴能分割三层小长方形,且最上一层正好能分割一个小长方形,
设第二层靠近点A的边为x,
根据三角形相似可得:,
解得,即第二层正好能分割两个小长方形,
设最下层靠近点A的边为,
根据三角形相似可得:,
解得,即最下层正好能分割三个小长方形,
∴按如图方式分割成的小长方形零件最多有个,
故答案为:B.
【分析】 当最上层的小长方形的一边与AB、AC交于点E、F时,EF∥BC,AD⊥BC于D,交EF于G,则△AEF∽△ABC,由相似三角形对应边成比例建立方程可求出AG的长,然后根据DG=AD-AG可求出DG的长, 所以△ABC能分割三层小长方形,且最上一层正好能分割一个小长方形,设第二层靠近点A的边为x,根据相似三角形对应边成比例建立方程求出x=10,即第二层正好能分割两个小长方形,设最下层靠近点A的边为y,根据相似三角形对应边成比例建立方程求出y=15,即最下层正好能分割三个小长方形,从而即可得出答案.
二、填空题(每小题3分,共15分)
11. 已知,则 .
【答案】
【知识点】比例的性质
【解析】【解答】解:∵设,
∴a=3k,b=4k,
∴.
故答案为:.
【分析】根据等比的性质,设,则a=3k,b=4k,然后代入待求式子,合并后约分化简即可.
12.如图,在等边中,点在BC上,,把沿直线MN对折,使点恰好落在点,则 .
【答案】
【知识点】等边三角形的性质;轴对称的性质;相似三角形的判定与性质
【解析】【解答】解:∵BD:DC=2:3,
∴设BD=2a,则CD=3a,BC=5a.
∵△ABC是等边三角形,
∴AB=BC=AC=5a,∠ABC=∠ACB=∠BAC=60°,
由折叠的性质可知:MN是线段AD的垂直平分线,
∴AM=DM,AN=DN,
∴BM+MD+BD=7a,DN+NC+DC=8a,
∵∠MDN=∠BAC=∠ABC=60°,
∴∠NDC+∠MDB=∠BMD+∠MDB=120°,
∴∠NDC=∠BMD,
∵∠ABC=∠ACB=60°,
∴△BMD∽△CDN,
∴(BM+MD+BD):(DN+NC+CD)=MD:DN=AM:AN,
即AM:AN=7:8,
故答案为: .
【分析】设BD=2a,则CD=3a,根据折叠的性质可得AM=DM,AN=DN,根据等边三角形的性质准备条件,证△BMD∽△CDN,根据相似三角形周长的性质求解即可。
13.利用无人机探照灯测量坡面的角度.如图,一架无人机探照灯在点处,测得它的下边缘光线DA落在坡脚点处,上边缘光线DB落在斜坡点处,此时无人机离地面6米,将无人机沿水平方向前进2.5米到达点处,探照灯的上下边缘光线EC,EB落在斜坡B,C处,,此时点恰好在的正上方,现测得,则 .
【答案】
【知识点】相似三角形的应用;锐角三角函数的定义
【解析】【解答】解:如图,连接,作于,
点恰好在的正上方,
是直角三角形,
又,,
根据勾股定理得,
,
∵ ,
,,
,
,
又∵,
,
,
,
,
,,
,
,
,
,
,
故答案为:.
【分析】通过做辅助线,构造直角,根据勾股定理求出的长,易证,依据相似的性质得出,求出BE,作于,由,列比例解出和,进而求出,根据,,进而求出
14.已知:中,是中线,点在上,且,.则 .
【答案】
【知识点】三角形的外角性质;等腰三角形的判定与性质;相似三角形的判定与性质
【解析】【解答】解:是边上的中线,
.
,
.
.
,
.
又,
.
.
.
.
.
故答案为:
【分析】本题考查相似三角形的判定与性质、等腰三角形的性质、三角形外角与内角的关系.先利用等腰三角形的性质,三角形外角与内角的关系可推出,再根据已知条件可证明,利用相似三角形的性质可得:,化简可用表示出,再代入比例式可求出答案.
15.如图,矩形ABCD中,AB=1,AD=2,连接BD,M、N分别为边AD、BC上的动点,且MN⊥BD于点P,连接DN、BM,则DN+BM的最小值为 。
【答案】
【知识点】平行四边形的性质;相似三角形的判定与性质;将军饮马模型-一线两点(一动两定)
【解析】【解答】解:如图,过点M作ME⊥BC,垂足为点E,
∵四边形ABCD是矩形,
∴∠A=∠ABC=∠BCD=∠CDA=90°,
∴四边形ABEM和四边形CDME均为矩形,
∴ME=AB=1,∠MPD+∠PDM=90°,
又∵MN⊥BD,
∴∠EMN+∠MPD=90°,
∴∠EMN=∠ADB,
∴在Rt△BAD和Rt△NEM中,
,
∴,解得:NE=,
以MN和BM作为平行四边形的两边向右侧构造平行四边形MBGN,过点G作HF⊥AB交AB延长线于点F,交DC延长线于点H,
由同角余角相等,即同理可证∠FBG=∠ADB,四边形BFHC为矩形,
∴BG=MN,NG=BM,FH=BC,BF=CH,
又∵BG=MN,∠F=∠MEN=90°,
∴△BFH≌△MEN(AAS),
∴CH=BF=ME=1,FG=NE=,HG=HF-FG=BC-FG=,
在Rt△DHG中,DG=,
又∵ DN+BM=DN+NG≥DG,
当且仅当D、N、G三点共线时,.
故答案为:.
【分析】利用MN⊥BD先分析边角关系,构造相似或利用同角三角函数值,即分析得MN为定长,故目标线段最值为“造桥选址”最值问题,即构造平行四边形的性质进行线段转移,将双动点转换为单动点的“将军饮马”线段和最值,利用勾股定理构造直角解之即可.
三、解答题(共8小题。共75分)
16.(8分)如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,每个小正方形的边长都为1.
(1)在图上标出位似中心D的位置,并写出该位似中心D的坐标是 ;
(2)求△ABC与△A′B′C′的面积比.
【答案】解:(1)如图:D(7,0);
(2)∵△ABC∽△A′B′C′
∴
【知识点】相似三角形的性质;作图﹣位似变换
【解析】【分析】考查位似.
17.(7分)如图,在中,,,点D,E分别在边上,且,.求证:.
【答案】【解答】
解:∵,,,,∴,,
∴,,
∴,
又∵,
∴.
【知识点】相似三角形的判定
【解析】【分析】首先求出,的长,再求出,又因为,根据相似三角形的判定可证得
18.(8分)如图,在中,,点是的中点,点是的中点,过点A作交的延长线于点F,交于点.
(1)求证:四边形是矩形;
(2)若,,则的面积为 .
【答案】(1)证明:,
,
∵点E是的中点,
,
在和中,
,
;
,点是线段的中点,
,,
,AF=CD,
四边形是矩形;
(2)
【知识点】等腰三角形的性质;矩形的判定;相似三角形的判定与性质
【解析】【解答】(2)解:根据(1)得,∴根据勾股定理可得,
,,
,
,
,
,
,
.
故答案为:.
【分析】(1)由二直线平行,内错角相等可得∠AFE=∠DBE,由中点定义可得AE=DE,从而可用“AAS”证出△BDE≌△FAE,由全等三角形的对应边相等可得AF=BD,再根据等腰三角形的三线合一可得AD⊥BC,BD=CD,则AF=CD,从而即可得到平行四边形ADCF是矩形;
(2)在Rt△ABD中,用勾股定理求得BD的长,从而求得AF=BD=2,BC=2BD=4,根据三角形面积公式算出△ABC的面积;由平行于三角形一边得直线,截其它两边的延长线,所截的三角形与原三角形相似得△AGF∽△CGB,利用相似三角形的对应边成比例得到,然后格局同高三角形的面积之比等于对应底之比可得,最后由求解即可.
19.(9分)图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.的三个顶点都是格点,只用无刻度的直尺,分别在给定的网格中按下列要求作图,保留作图痕迹,不写作法.
(1)以点为位似中心,把缩小为原来的,得到,在图①中画出;
(2)在图②中,作出的高线;
(3)在图③中,在边上作点,使线段的长度为.
【答案】(1)见详解
(2)见详解
(3)见详解
【知识点】三角形的角平分线、中线和高;勾股定理;作图﹣位似变换
【解析】【解答】(1)如图所示:即为所求;
(2)如图所示,即为所求;
(3)如图所示:点即为所求.
【分析】(1)根据题意再结合网格,找到、中点,然后相连接,即可得到答案;
(2)根据题意再结合网格,利用直角三角形中两锐角互余的性质,即可得到答案;
(3)根据题意再结合网格,求出的长度为,,即,找到的五等分点,即可得到答案.
20.(9分)根据以下素材,探索解决问题.
测量旗杆的高度
素材1 可以利用影子测量旗杆的高度.如图1,光线,DN,BM分别是旗杆和小陈同学在同一时刻的影子.
素材2 可以利用镜子测量旗杆的高度.如图2,小陈同学从镜子E中刚好可以看见旗杆的顶端C,测得.
素材3 可以利用标杆测量旗杆的高度.如图3,点G,P,C在同一直线上,标杆,测得,.(说明:小陈同学、旗杆CD与标杆PQ均垂直于地面,小陈同学的眼睛G离地面的距离)
(1)任务1 利用素材1证明△ABM△CDN;
(2)任务2 在素材2中,小陈同学还要测量图中哪条线段的长度(旗杆无法直接测量),才能求出旗杆的高度?若把该线段的长度记为a,请你用含a的式子表示出旗杆的高度;
(3)任务3 利用素材3求出旗杆的高度.
【答案】(1)证明:由题意知:,,
即,
∵,
∴,
∴.
(2)解:小陈同学还要测量图中线段DE的长度,记为a.
由题意知:,
∵,,
∴,
∴.
∴,
∵,,,
∴.
(3)解:过点G作于点H,交PQ于点F.
由题意知:,,,
即,
,,
∵,,
∴,
∴,
∴,
∴,
∴,
∴.
【知识点】相似三角形的应用
【解析】【分析】(1)由题意得到:,然后根据平行线的性质得到:,进而即可求证;
(2)把线段DE的长度记为a,由题意得到:,进而证明,得到:,进而可得到CD的长;
(3)过点G作于点H,交PQ于点F,由题意得到:,,,进而求出PF的长度,然后根据垂直的定义和平行线的性质即可证明,得到:,进而即可求出CD的长.
21.(9分)阅读理解:
如图1,若在四边形ABCD的边AB上任取一点E(点E与点A,B不重合),分别连结ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,若∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,请直接写出的值.
图1 图2 图3
【答案】解:(1)点E是四边形ABCD的边AB上的相似点.
理由:∵∠A=55°,
∴∠ADE+∠DEA=125°.
∵∠DEC=55°,
∴∠BEC+∠DEA=125°.
∴∠ADE=∠BEC.
∵∠A=∠B,
∴△ADE∽△BEC.
∴点E是四边形ABCD的AB边上的相似点
(2)作图如下:
图1图2
(3).
【知识点】矩形的性质;梯形;相似三角形的判定与性质
【解析】【分析】(1)要证明点E是四边形ABCD的边AB上的相似点,只要证明有一组三角形相似就行,很容易证明△ADE∽△BEC,所以问题得解.
(2)根据两个直角三角形相似得到强相似点的两种情况即可.
(3)因为点E是梯形ABCD的边AB上的一个强相似点,所以就有相似三角形出现,根据相似三角形的对应线段成比例,可以判断出BC和AB的数量关系,从而可求出解.
21.(12分) 小明在学习过程中,对教材的一个习题做如下探究:
(1)【习题回顾】:如图,在等边三角形ABC的AC、BC边上各取一点P,Q使AP=CQ,AQ,BP相交于点O,求∠BOQ的度数.请你解答该习题.
(2)【拓展延伸】:如图1,在等腰Rt△ABC的AC,BC边上各取一点P,Q,使AP=CQ,BP平分∠ABC, AQ=,∠BAC=90°,求BP的长.小明的思路:过点A作AG∥BC交BP延长线于点G,证明△AQC≌△GPA,
(3)如图2,在Rt△ABC的AC、BC边上各取一点P、Q,使CQ=2AP,BP平分∠ABC,,∠BAC=90°,求AQ,BP的数量关系,请你解答小明提出的问题.
【答案】(1)解:在等边△ABC中,AB=AC,∠BAP=∠C=60°,AP=CQ,
∴△ABP≌△CAQ(SAS),
∴∠ABP=∠CAQ.
∵∠BOQ=∠BAO+∠ABP,
∴∠BOQ=∠BAO+∠CAQ=∠BAC=60°;
(2)解:过点A作AG∥BC交BP的延长线于点G,
∴∠PAG=∠C,∠PBC=∠G,
∵BP平分∠ABC,
∴∠PBC=∠ABP,
∴∠G=∠ABP,
∴AG=AB,
∵AC=AB,
∴AG=AC,
∵AP=CQ,
∴△CAQ≌△AGP(SAS),
∴PG=AQ=.
∵AG∥BC,
∴△APG∽△CPB,
∴,
而,
∴,
∴,
∵PG=,
∴BP=2;
(3)解:如图2,过点A作AG∥BC交BP的延长线于点G,
由(1)知∠PAG=∠C,AG=AB,
∵,
∴,
∵CQ=2AP,
∴,
∴△APG∽△CQA,
∴,
∴,
Rt△ABC中,,
∴,
∴,
∵AG∥BC,
∴△APG∽△CPB,
∴,
∴,
∴,
∴2BP=AQ.
【知识点】角平分线的性质;相似三角形的判定与性质;三角形全等的判定-SAS
【解析】【分析】(1)根据三角形全等的判定(SAS)和性质,可得∠ABP=∠CAQ;根据交的计算,即可求出∠BOQ的度数;
(2)根据角平分线的性质,可得∠PBC=∠ABP;根据三角形全等的判定(SAS)和性质,可得PG=AQ;根据三角形相似的判定和性质,可列比例式,进而求出BP的值;
(3)根据三角形相似的判定和性质,可列比例式,得到,,进而可得AQ和BP的数量关系.
22.(12分)如图,在平面直角坐标系中,抛物线:经过点和.
(1)求抛物线的对称轴.
(2)当时,将抛物线向左平移2个单位,再向下平移1个单位,得到抛物线.
①求抛物线的解析式.
②设抛物线与轴交于,两点(点在点的右侧),与轴交于点,连接.点为第一象限内抛物线上一动点,过点作于点.设点的横坐标为.是否存在点,使得以点,,为顶点的三角形与相似,若存在,求出的值;若不存在,请说明理由.
【答案】(1)x=2.5;(2)①;②1或
【分析】(1)根据函数图像所过的点的特点结合函数性质,可知两点中点横坐标即为对称轴;
(2)①根据平移可得已知点平移后点的坐标,平移过程中a的值不发生改变,所以利用交点式可以求出函数解析式;
②根据条件求出A、B、C、D四点的坐标,由条件可知三角形相似有两种情况,分别讨论两种情况,根据相似的性质可求出m的值.
【详解】解:(1)因为抛物线图像过(1,1)、(4,1)两点,
这两点的纵坐标相同,根据抛物线的性质可知,对称轴是x=(1+4)÷2=2.5,;
(2)①将点(1,1)、(4,1)向左平移2个单位,再向下平移1个单位,得到(-1,0),(2,0),将点(-1,0),(2,0),a=-1,
根据交点式可求出C1二次函数表达式为;
②根据①中的函数关系式,可得A(2,0),B(-1,0),C(0,2),D(m,),且m>0
由图像可知∠BOC=∠DEO=90°,
则以点,,为顶点的三角形与相似有两种情况,
(i)当△ODE∽△BCO时,
则,即,
解得m=1或-2(舍),
(ii)当△ODE∽△CBO时,
则,即,
解得
所以满足条件的m的值为1或.
【点睛】本题主要考查了一元二次函数图形的平移、表达式求法、相似三角形等知识点,熟练运用数形结合是解决问题的关键.
23 .(13分)小明在学习过程中,对教材的一个习题做如下探究:
(1)【习题回顾】:如图,在等边三角形ABC的AC、BC边上各取一点P,Q使AP=CQ,AQ,BP相交于点O,求∠BOQ的度数.请你解答该习题.
(2)【拓展延伸】:如图1,在等腰Rt△ABC的AC,BC边上各取一点P,Q,使AP=CQ,BP平分∠ABC, AQ=,∠BAC=90°,求BP的长.小明的思路:过点A作AG∥BC交BP延长线于点G,证明△AQC≌△GPA,
(3)如图2,在Rt△ABC的AC、BC边上各取一点P、Q,使CQ=2AP,BP平分∠ABC,,∠BAC=90°,求AQ,BP的数量关系,请你解答小明提出的问题.
【答案】(1)解:在等边△ABC中,AB=AC,∠BAP=∠C=60°,AP=CQ,
∴△ABP≌△CAQ(SAS),
∴∠ABP=∠CAQ.
∵∠BOQ=∠BAO+∠ABP,
∴∠BOQ=∠BAO+∠CAQ=∠BAC=60°;
(2)解:过点A作AG∥BC交BP的延长线于点G,
∴∠PAG=∠C,∠PBC=∠G,
∵BP平分∠ABC,
∴∠PBC=∠ABP,
∴∠G=∠ABP,
∴AG=AB,
∵AC=AB,
∴AG=AC,
∵AP=CQ,
∴△CAQ≌△AGP(SAS),
∴PG=AQ=.
∵AG∥BC,
∴△APG∽△CPB,
∴,
而,
∴,
∴,
∵PG=,
∴BP=2;
(3)解:如图2,过点A作AG∥BC交BP的延长线于点G,
由(1)知∠PAG=∠C,AG=AB,
∵,
∴,
∵CQ=2AP,
∴,
∴△APG∽△CQA,
∴,
∴,
Rt△ABC中,,
∴,
∴,
∵AG∥BC,
∴△APG∽△CPB,
∴,
∴,
∴,
∴2BP=AQ.
【知识点】角平分线的性质;相似三角形的判定与性质;三角形全等的判定-SAS
【解析】【分析】(1)根据三角形全等的判定(SAS)和性质,可得∠ABP=∠CAQ;根据交的计算,即可求出∠BOQ的度数;
(2)根据角平分线的性质,可得∠PBC=∠ABP;根据三角形全等的判定(SAS)和性质,可得PG=AQ;根据三角形相似的判定和性质,可列比例式,进而求出BP的值;
(3)根据三角形相似的判定和性质,可列比例式,得到,,进而可得AQ和BP的数量关系.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
