2023-2024学年山东省青岛十七中高三(上)期末数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年山东省青岛十七中高三(上)期末数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 94.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 09:19:02 | ||
图片预览




文档简介
2023-2024学年山东省青岛十七中高三(上)期末数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知,则( )
A. B. C. D.
2.已知集合,则( )
A. B. C. D.
3.若是抛物线位于第一象限的点,是抛物线的焦点,,则直线的斜率为( )
A. B. C. D.
4.第届夏季奥运会预计在年月日至月日在法国巴黎举办,这届奥运会将新增电子竞技和冲浪两个竞赛项目以及滑板等个表演项目现有三个场地,,分别承担竞赛项目与表演项目比赛,其中电子竞技和冲浪两个项目仅能,两地承办,且各自承办其中一项个表演项目分别由,,三个场地承办,且每个场地至少承办其中一个项目,则不同的安排方法有( )
A. 种 B. 种 C. 种 D. 种
5.若数列的首项,且满足,则( )
A. B. C. D.
6.已知,若,则( )
A. B. C. D.
7.一个封闭的圆台容器容器壁厚度忽略不计的上底面半径为,下底面半径为,母线与底面所成的角为在圆台容器内放置一个可以任意转动的正方体,则此正方体棱长的最大值是( )
A. B. C. D.
8.定义在上的可导函数,满足,且,若,,,则,,的大小关系是( )
A. B. C. D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.新式茶饮是指以上等茶叶通过萃取浓缩液,再根据消费者偏好,添加牛奶、坚果、柠檬等小料调制而成的饮料如图为年我国消费者购买新式茶饮的频次扇形图及月均消费新式茶饮金额的条形图根据所给统计图,下列结论中正确的是( )
A. 每周都消费新式茶饮的消费者占比不到
B. 每天都消费新式茶饮的消费者占比超过
C. 月均消费新式茶饮元的消费者占比超过
D. 月均消费新式茶饮超过元的消费者占比超过
10.有关平面向量的说法,下列错误的是( )
A. 若,,则
B. 若与共线且模长相等,则
C. 若且与方向相同,则
D. 恒成立
11.已知定义域在上的函数满足:是奇函数,且,当,,则下列结论正确的是( )
A. 的周期 B.
C. 在上单调递增 D. 是偶函数
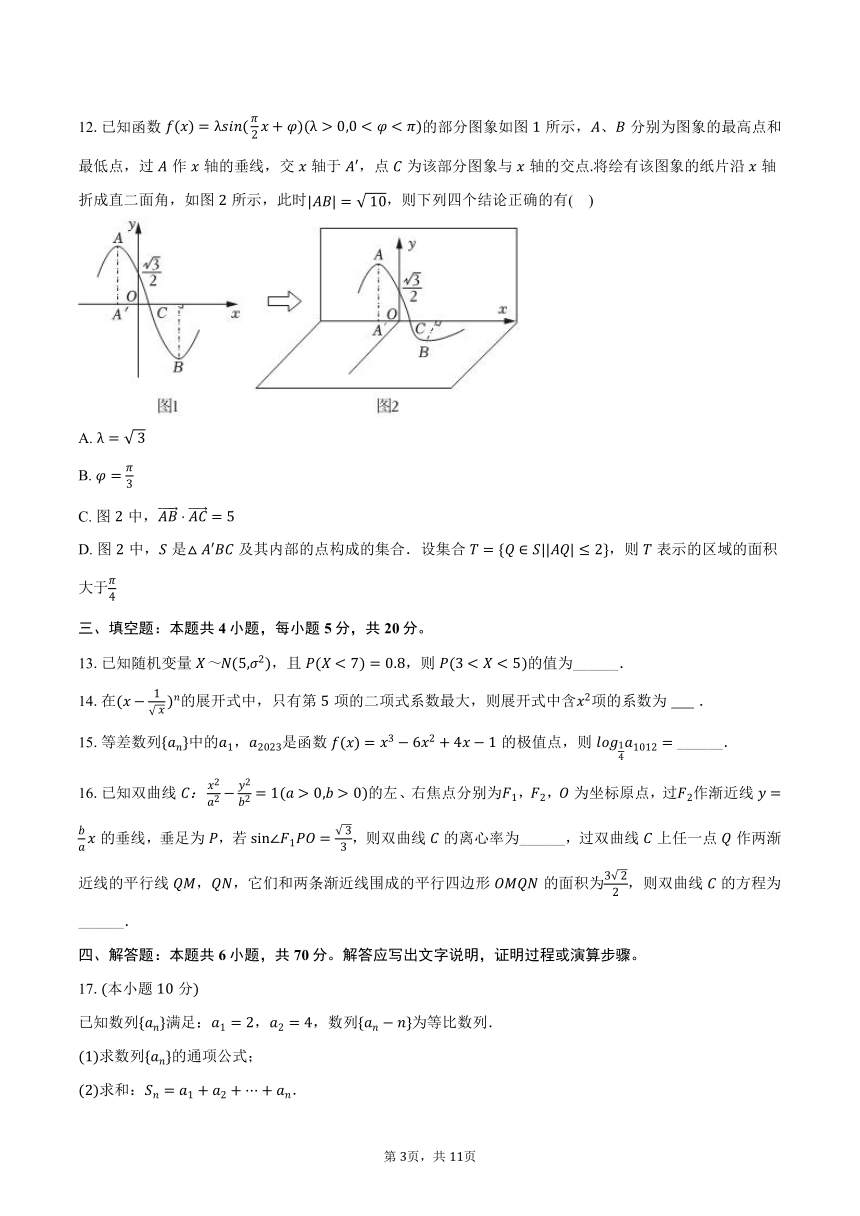
12.已知函数的部分图象如图所示,、分别为图象的最高点和最低点,过作轴的垂线,交轴于,点为该部分图象与轴的交点将绘有该图象的纸片沿轴折成直二面角,如图所示,此时,则下列四个结论正确的有( )
A.
B.
C. 图中,
D. 图中,是及其内部的点构成的集合.设集合,则表示的区域的面积大于
三、填空题:本题共4小题,每小题5分,共20分。
13.已知随机变量,且,则的值为______.
14.在的展开式中,只有第项的二项式系数最大,则展开式中含项的系数为 .
15.等差数列中的,是函数的极值点,则 ______.
16.已知双曲线的左、右焦点分别为,,为坐标原点,过作渐近线的垂线,垂足为,若,则双曲线的离心率为______,过双曲线上任一点作两渐近线的平行线,,它们和两条渐近线围成的平行四边形的面积为,则双曲线的方程为______.
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知数列满足:,,数列为等比数列.
求数列的通项公式;
求和:.
18.本小题分
在中,角,,所对的边长为,,,,.
Ⅰ若,求的面积;
Ⅱ是否存在正整数,使得为钝角三角形?若存在,求出的值;若不存在,说明理由.
19.本小题分
某单位组织“乡村振兴”知识竞赛,有甲、乙两类问题每位参加比赛的选手先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误,则该选手比赛结束;若回答正确,则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该选手比赛结束甲类问题中的每个问题回答正确得分,否则得分;乙类问题中的每个问题回答正确得分,否则得分已知选手张某能正确回答甲类问题的概率为,能正确回答乙类问题的概率为,且能正确回答问题的概率与回答次序无关.
若选甲、乙两类问题是等可能的,求张某至少答对一道问题的概率;
如果答题顺序由张某选择,以累计得分多为决策依据,说明张某应选择先回答哪类问题.
20.本小题分
如图,在直角梯形中,为的中点,四边形为正方形,将沿折起,使点到达点,如图,为的中点,且,点为线段上的一点.
证明:;
当与夹角最小时,求平面与平面所成锐二面角的余弦值.
21.本小题分
已知椭圆:的离心率为,左右顶点分别为,是上异于,的点,满足,的斜率之积为.
求的方程;
,是椭圆上的两点在的左侧,,的斜率为,,且与相交于,求的取值范围.
22.本小题分
已知函数.
若,求的单调区间与极值
若当时,恒有,求的取值范围;
设,证明:.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:因为,,数列为等比数列,
所以,,则,
即是以为首项,为公比的等比数列,
所以,则.
.
18.解:,
根据正弦定理可得,
,,
,,,
在中,运用余弦定理可得,
,
,
.
,
为钝角三角形时,必角为钝角,
,
,
,
,
三角形的任意两边之和大于第三边,
,即,即,
,
为正整数,
.
19.解:记为“张某选择甲类问题”,为“张某答对所选问题”,为“张某至少答对一道问题”,为“张某选择乙类问题”,为“张某未答对所选问题”,为“张某一道问题都没答对”,
易知,,,,,
所以,
则;
若张某先回答甲类问题,
此时张某的累计得分的可能取值为,,,
因为张某能正确回答甲类问题的概率为,能正确回答乙类问题的概率为,
所以,,,
则的分布列为:
故E;
若张某先回答乙类问题,
此时张某的累计得分的可能取值为,,,
所以,,,
则,
因为.
所以,以累计得分多为决策依据,张某应选择先回答甲类问题.
20.解:由为正方形,得,,
为的中点,,
,即.
设,建立以为坐标原点的空间直角坐标系,如图所示,
则,,,,,.
点在线段上,设,
又,,
又,,
又,,
又,,
,即,
由知,,
,
当时,最大,最小,此时.
由题知,平面的一个法向量为,
设平面的一个法向量,
,即,
取,得,则,
.
平面与平面所成锐二面角的余弦值为.
21.解:设,,,
因为,的斜率之积为,
所以,
因为是上的点,所以,
所以,
故,又,所以,又,
解得:,,
故椭圆的方程为:;
设,的斜率为,,,的斜率为,,
因为,在椭圆上,所以,,
所以,
同理,
所以,又,所以,
设的方程为:,的方程为:,
联立,则,解得:,
联立,可得:,
因为直线与椭圆交于,两点,
所以,解得:,
联立,可得:,
因为直线与椭圆交于,两点,
即,解得:,
由可得:,
即,
解得:,
所以
,
因为,所以,,
的取值范围为.
22.解:当时,,
,
令,得,
所以在上,单调递减,
在上,单调递增,
所以在处取得极小值,无极大值.
所以的单调减区间为,增区间为,极小值为,无极大值.
令,
则当时,,
,
,
令,则,
,
当时,,
则在上存在点,使得当时,,
在上单调递增,
在上单调递增,
此时,
在上单调递增,则,不合题意;
当时,,
令,则,
在上单调递减,
,即,
,则,
,
在上单调递减,
在上单调递减,
,
在上单调递减,
,满足题意,
综上所述:的取值范围为.
证明:当时,由知:当时,恒成立,
令,则,,
,
,即对任意恒成立,
对,,即,
.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知,则( )
A. B. C. D.
2.已知集合,则( )
A. B. C. D.
3.若是抛物线位于第一象限的点,是抛物线的焦点,,则直线的斜率为( )
A. B. C. D.
4.第届夏季奥运会预计在年月日至月日在法国巴黎举办,这届奥运会将新增电子竞技和冲浪两个竞赛项目以及滑板等个表演项目现有三个场地,,分别承担竞赛项目与表演项目比赛,其中电子竞技和冲浪两个项目仅能,两地承办,且各自承办其中一项个表演项目分别由,,三个场地承办,且每个场地至少承办其中一个项目,则不同的安排方法有( )
A. 种 B. 种 C. 种 D. 种
5.若数列的首项,且满足,则( )
A. B. C. D.
6.已知,若,则( )
A. B. C. D.
7.一个封闭的圆台容器容器壁厚度忽略不计的上底面半径为,下底面半径为,母线与底面所成的角为在圆台容器内放置一个可以任意转动的正方体,则此正方体棱长的最大值是( )
A. B. C. D.
8.定义在上的可导函数,满足,且,若,,,则,,的大小关系是( )
A. B. C. D.
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.新式茶饮是指以上等茶叶通过萃取浓缩液,再根据消费者偏好,添加牛奶、坚果、柠檬等小料调制而成的饮料如图为年我国消费者购买新式茶饮的频次扇形图及月均消费新式茶饮金额的条形图根据所给统计图,下列结论中正确的是( )
A. 每周都消费新式茶饮的消费者占比不到
B. 每天都消费新式茶饮的消费者占比超过
C. 月均消费新式茶饮元的消费者占比超过
D. 月均消费新式茶饮超过元的消费者占比超过
10.有关平面向量的说法,下列错误的是( )
A. 若,,则
B. 若与共线且模长相等,则
C. 若且与方向相同,则
D. 恒成立
11.已知定义域在上的函数满足:是奇函数,且,当,,则下列结论正确的是( )
A. 的周期 B.
C. 在上单调递增 D. 是偶函数
12.已知函数的部分图象如图所示,、分别为图象的最高点和最低点,过作轴的垂线,交轴于,点为该部分图象与轴的交点将绘有该图象的纸片沿轴折成直二面角,如图所示,此时,则下列四个结论正确的有( )
A.
B.
C. 图中,
D. 图中,是及其内部的点构成的集合.设集合,则表示的区域的面积大于
三、填空题:本题共4小题,每小题5分,共20分。
13.已知随机变量,且,则的值为______.
14.在的展开式中,只有第项的二项式系数最大,则展开式中含项的系数为 .
15.等差数列中的,是函数的极值点,则 ______.
16.已知双曲线的左、右焦点分别为,,为坐标原点,过作渐近线的垂线,垂足为,若,则双曲线的离心率为______,过双曲线上任一点作两渐近线的平行线,,它们和两条渐近线围成的平行四边形的面积为,则双曲线的方程为______.
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知数列满足:,,数列为等比数列.
求数列的通项公式;
求和:.
18.本小题分
在中,角,,所对的边长为,,,,.
Ⅰ若,求的面积;
Ⅱ是否存在正整数,使得为钝角三角形?若存在,求出的值;若不存在,说明理由.
19.本小题分
某单位组织“乡村振兴”知识竞赛,有甲、乙两类问题每位参加比赛的选手先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误,则该选手比赛结束;若回答正确,则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该选手比赛结束甲类问题中的每个问题回答正确得分,否则得分;乙类问题中的每个问题回答正确得分,否则得分已知选手张某能正确回答甲类问题的概率为,能正确回答乙类问题的概率为,且能正确回答问题的概率与回答次序无关.
若选甲、乙两类问题是等可能的,求张某至少答对一道问题的概率;
如果答题顺序由张某选择,以累计得分多为决策依据,说明张某应选择先回答哪类问题.
20.本小题分
如图,在直角梯形中,为的中点,四边形为正方形,将沿折起,使点到达点,如图,为的中点,且,点为线段上的一点.
证明:;
当与夹角最小时,求平面与平面所成锐二面角的余弦值.
21.本小题分
已知椭圆:的离心率为,左右顶点分别为,是上异于,的点,满足,的斜率之积为.
求的方程;
,是椭圆上的两点在的左侧,,的斜率为,,且与相交于,求的取值范围.
22.本小题分
已知函数.
若,求的单调区间与极值
若当时,恒有,求的取值范围;
设,证明:.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:因为,,数列为等比数列,
所以,,则,
即是以为首项,为公比的等比数列,
所以,则.
.
18.解:,
根据正弦定理可得,
,,
,,,
在中,运用余弦定理可得,
,
,
.
,
为钝角三角形时,必角为钝角,
,
,
,
,
三角形的任意两边之和大于第三边,
,即,即,
,
为正整数,
.
19.解:记为“张某选择甲类问题”,为“张某答对所选问题”,为“张某至少答对一道问题”,为“张某选择乙类问题”,为“张某未答对所选问题”,为“张某一道问题都没答对”,
易知,,,,,
所以,
则;
若张某先回答甲类问题,
此时张某的累计得分的可能取值为,,,
因为张某能正确回答甲类问题的概率为,能正确回答乙类问题的概率为,
所以,,,
则的分布列为:
故E;
若张某先回答乙类问题,
此时张某的累计得分的可能取值为,,,
所以,,,
则,
因为.
所以,以累计得分多为决策依据,张某应选择先回答甲类问题.
20.解:由为正方形,得,,
为的中点,,
,即.
设,建立以为坐标原点的空间直角坐标系,如图所示,
则,,,,,.
点在线段上,设,
又,,
又,,
又,,
又,,
,即,
由知,,
,
当时,最大,最小,此时.
由题知,平面的一个法向量为,
设平面的一个法向量,
,即,
取,得,则,
.
平面与平面所成锐二面角的余弦值为.
21.解:设,,,
因为,的斜率之积为,
所以,
因为是上的点,所以,
所以,
故,又,所以,又,
解得:,,
故椭圆的方程为:;
设,的斜率为,,,的斜率为,,
因为,在椭圆上,所以,,
所以,
同理,
所以,又,所以,
设的方程为:,的方程为:,
联立,则,解得:,
联立,可得:,
因为直线与椭圆交于,两点,
所以,解得:,
联立,可得:,
因为直线与椭圆交于,两点,
即,解得:,
由可得:,
即,
解得:,
所以
,
因为,所以,,
的取值范围为.
22.解:当时,,
,
令,得,
所以在上,单调递减,
在上,单调递增,
所以在处取得极小值,无极大值.
所以的单调减区间为,增区间为,极小值为,无极大值.
令,
则当时,,
,
,
令,则,
,
当时,,
则在上存在点,使得当时,,
在上单调递增,
在上单调递增,
此时,
在上单调递增,则,不合题意;
当时,,
令,则,
在上单调递减,
,即,
,则,
,
在上单调递减,
在上单调递减,
,
在上单调递减,
,满足题意,
综上所述:的取值范围为.
证明:当时,由知:当时,恒成立,
令,则,,
,
,即对任意恒成立,
对,,即,
.
第1页,共1页
同课章节目录
