人教版六年级下册数学数学广角——鸽巢问题 课件(共20张PPT)
文档属性
| 名称 | 人教版六年级下册数学数学广角——鸽巢问题 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 13:52:28 | ||
图片预览





文档简介
(共20张PPT)
给大家表演一个“魔术”。一副牌,取出大小王,还剩52张,你们5人每人随意抽一张,我知道至少有2张牌是同花色的。相信吗?
《义务教育教科书·数学》人教版六年级下册
数学广角--鸽巢问题(一)
把4支铅笔放进3个笔筒中,不管怎么放,总有1个笔筒里至少有2支铅笔。
“总有”和“至少”是什么意思?
总有 表示一定有
至少 表示最少
二、探索新知
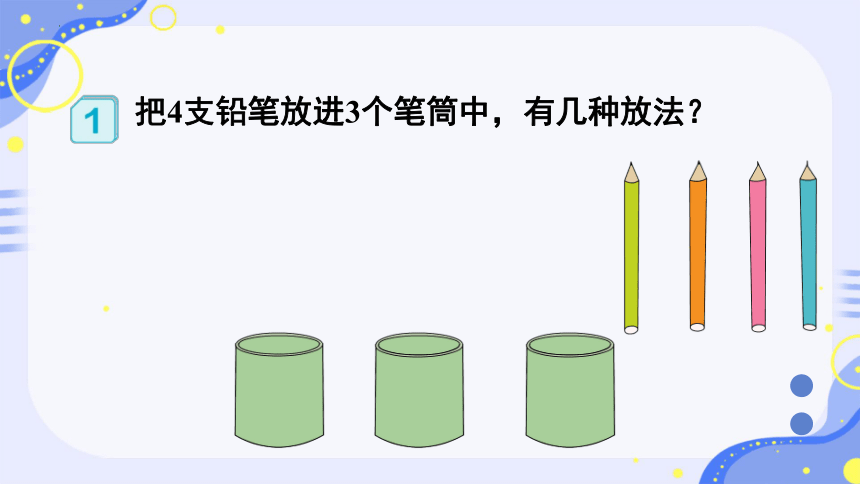
把4支铅笔放进3个笔筒中,有几种放法?
要求:
1.所有的笔必须放进笔筒,不考虑笔筒的顺序,没有放笔的用0表示。
2.想一想,怎样才能做到不重复,不遗漏。
3.分组合作,把摆放结果记录在草稿本上。
小组合作
把四支铅笔放进三个笔筒中,有几种放法
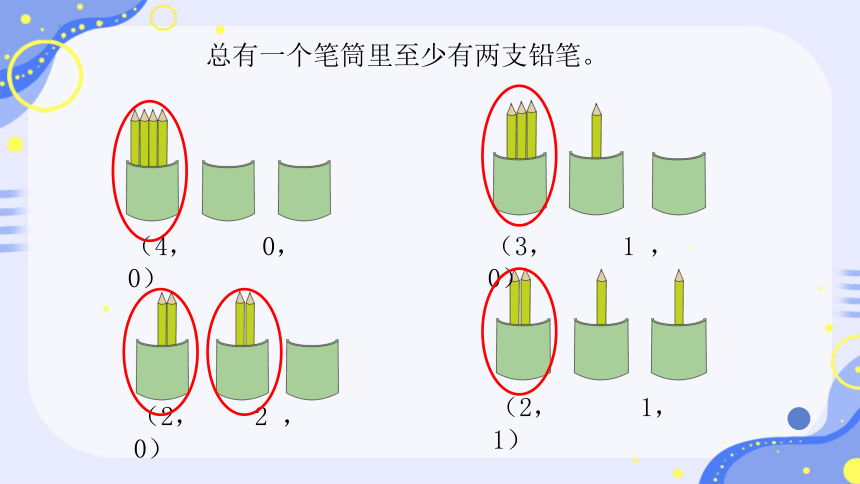
(2, 1, 1)
总有一个笔筒里至少有两支铅笔。
(4, 0, 0)
(2, 2 , 0)
(3, 1 , 0)
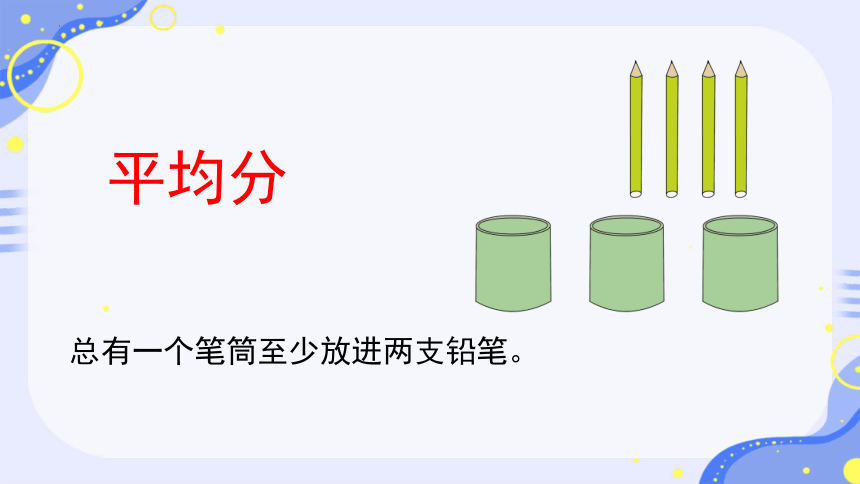
平均分
总有一个笔筒至少放进两支铅笔。
把5支笔放到4个笔筒里,总有一个笔筒里至少有( )支笔
自测 :
把100支笔放到99个笔筒里呢? ......
把6支笔放到5个笔筒里,总有一个笔筒里至少有( )支笔
把7支笔放到6个笔筒里,总有一个笔筒里至少有( )支笔
总结:
只要笔的数量比笔筒的数量多1,不管怎么放,总有一个笔筒里至少有2支笔。
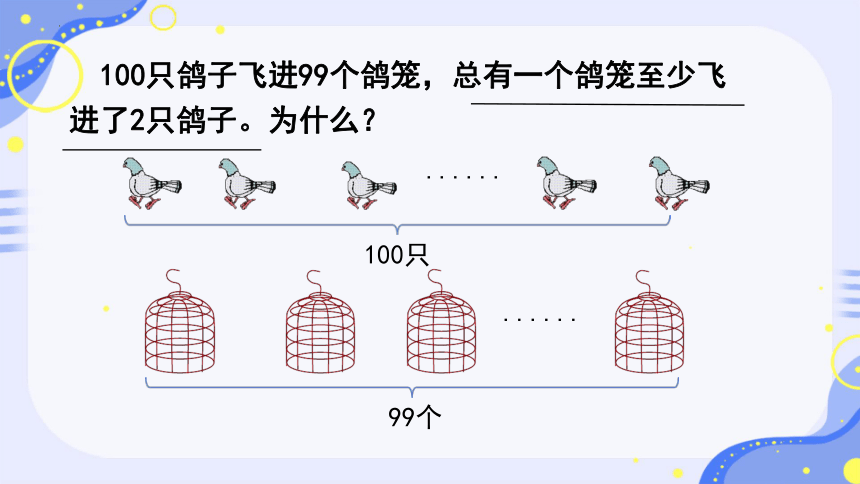
100只鸽子飞进99个鸽笼,总有一个鸽笼至少飞进了2只鸽子。为什么?
......
......
99个
100只
把9个苹果放进个4抽屉里,不管怎么放,总有一个抽屉里至少放进多少个个苹果呢?
100只鸽子飞进99个鸽笼:
4支铅笔放进3个笔筒:
9个苹果放进4个抽屉里。
物体数
抽屉数
7只鸽子飞进了3个鸽笼,不管怎么飞,总有一个鸽笼至少飞进了多少只鸽子?
8只鸽子飞进了3个鸽笼,不管怎么飞,总有一个鸽笼至少飞进了多少只鸽子?
“鸽巢原理”又称“抽屉原理”,是组合数学中的一个重要原理,它最早是由德国数学家狄利克雷提出并运用于解决数学问题中的,所以该原理又称“狄利克雷原理”。
狄利克雷
(1805-1859)
你知道吗?
1、8只鸽子飞入5个鸽巢,总有一个鸽笼至少飞进多少只鸽子?
三、知识运用
8 ÷ 5 =1 3
......
至少数:1 + 1 = 2(只)
答:总有一个鸽笼至少飞进2只鸽子。
2、9个苹果放进3个抽屉里,总有一个抽屉里至少放进多少个苹果
9 ÷ 3 = 3(本)
答:总有一个抽屉里至少放进3个苹果。
3、一副牌,取出大小王后,还剩52张,抽出5张牌,至少有2张牌是同花色的。你知道为什么了吗?
5 ÷ 4 =1 1
......
1 + 1 = 2 (张)
4、我们班有46名同学,其中至少有多少名同学是同一个月过生日?你是怎么想的?
思考:幼儿园有15名小朋友,每个小朋友都要有苹果,而且有一个小朋友至少要有2个苹果,老师至少要准备多少个苹果?
1、随意找13位同学,他们中至少有2个人的属相相同。为什么?(67页做一做第1题。)
五、作业布置:请你从两类作业中,任选一类作业完成。
A类:
1、5只鸽子飞进了3个鸽笼,总有一个鸽笼至少飞进了2只鸽子。为什么?(67页做一做第2题。)
B类:
2、有46个小朋友要进5间屋子,至少有几个小朋友要选择意见屋子?
2、从扑克牌中取出两张王牌,在剩下的52张扑克牌中任意挑选18张牌,至少有几张是同花色?
给大家表演一个“魔术”。一副牌,取出大小王,还剩52张,你们5人每人随意抽一张,我知道至少有2张牌是同花色的。相信吗?
《义务教育教科书·数学》人教版六年级下册
数学广角--鸽巢问题(一)
把4支铅笔放进3个笔筒中,不管怎么放,总有1个笔筒里至少有2支铅笔。
“总有”和“至少”是什么意思?
总有 表示一定有
至少 表示最少
二、探索新知
把4支铅笔放进3个笔筒中,有几种放法?
要求:
1.所有的笔必须放进笔筒,不考虑笔筒的顺序,没有放笔的用0表示。
2.想一想,怎样才能做到不重复,不遗漏。
3.分组合作,把摆放结果记录在草稿本上。
小组合作
把四支铅笔放进三个笔筒中,有几种放法
(2, 1, 1)
总有一个笔筒里至少有两支铅笔。
(4, 0, 0)
(2, 2 , 0)
(3, 1 , 0)
平均分
总有一个笔筒至少放进两支铅笔。
把5支笔放到4个笔筒里,总有一个笔筒里至少有( )支笔
自测 :
把100支笔放到99个笔筒里呢? ......
把6支笔放到5个笔筒里,总有一个笔筒里至少有( )支笔
把7支笔放到6个笔筒里,总有一个笔筒里至少有( )支笔
总结:
只要笔的数量比笔筒的数量多1,不管怎么放,总有一个笔筒里至少有2支笔。
100只鸽子飞进99个鸽笼,总有一个鸽笼至少飞进了2只鸽子。为什么?
......
......
99个
100只
把9个苹果放进个4抽屉里,不管怎么放,总有一个抽屉里至少放进多少个个苹果呢?
100只鸽子飞进99个鸽笼:
4支铅笔放进3个笔筒:
9个苹果放进4个抽屉里。
物体数
抽屉数
7只鸽子飞进了3个鸽笼,不管怎么飞,总有一个鸽笼至少飞进了多少只鸽子?
8只鸽子飞进了3个鸽笼,不管怎么飞,总有一个鸽笼至少飞进了多少只鸽子?
“鸽巢原理”又称“抽屉原理”,是组合数学中的一个重要原理,它最早是由德国数学家狄利克雷提出并运用于解决数学问题中的,所以该原理又称“狄利克雷原理”。
狄利克雷
(1805-1859)
你知道吗?
1、8只鸽子飞入5个鸽巢,总有一个鸽笼至少飞进多少只鸽子?
三、知识运用
8 ÷ 5 =1 3
......
至少数:1 + 1 = 2(只)
答:总有一个鸽笼至少飞进2只鸽子。
2、9个苹果放进3个抽屉里,总有一个抽屉里至少放进多少个苹果
9 ÷ 3 = 3(本)
答:总有一个抽屉里至少放进3个苹果。
3、一副牌,取出大小王后,还剩52张,抽出5张牌,至少有2张牌是同花色的。你知道为什么了吗?
5 ÷ 4 =1 1
......
1 + 1 = 2 (张)
4、我们班有46名同学,其中至少有多少名同学是同一个月过生日?你是怎么想的?
思考:幼儿园有15名小朋友,每个小朋友都要有苹果,而且有一个小朋友至少要有2个苹果,老师至少要准备多少个苹果?
1、随意找13位同学,他们中至少有2个人的属相相同。为什么?(67页做一做第1题。)
五、作业布置:请你从两类作业中,任选一类作业完成。
A类:
1、5只鸽子飞进了3个鸽笼,总有一个鸽笼至少飞进了2只鸽子。为什么?(67页做一做第2题。)
B类:
2、有46个小朋友要进5间屋子,至少有几个小朋友要选择意见屋子?
2、从扑克牌中取出两张王牌,在剩下的52张扑克牌中任意挑选18张牌,至少有几张是同花色?
