青岛版五年级上册数学《梯形的面积》教学 课件(共18张PPT)
文档属性
| 名称 | 青岛版五年级上册数学《梯形的面积》教学 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 14:06:03 | ||
图片预览






文档简介
(共18张PPT)
梯形的面积
【教学目标】
1.在自主探索、合作交流中经历梯形面积公式的推导过程,掌握梯形面积的计算方法,并能灵活运用公式解决相关的数学问题。
2.通过猜想、验证、实践等数学活动,发展空间观念和推理能力,获得解决问题的多种策略,感受数学方法的内在魅力。
3.通过探索活动,激发学习兴趣、培养严谨、科学的学习态度、勇于探索、乐于合作的精神。
【教学重点】理解并掌握梯形面积计算公式。
【教学难点】理解平行四边形的面积计算公式的推导过程。
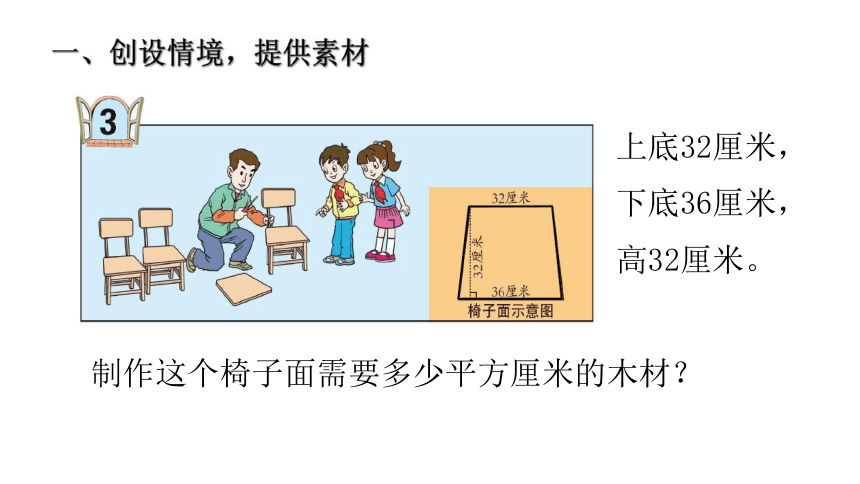
制作这个椅子面需要多少平方厘米的木材?
上底32厘米,
下底36厘米,
高32厘米。
1.试一试:借助学具剪一剪、拼一拼,自主探究梯形的面
积公式。
2.说一说:小组交流,把探究的过程互相说一说。
探究提示
箕
田
术
曰
并
踵
舌
而
半
之
以
乘
正
从
箕
田
术
曰
并
踵
舌
而
半
之
以
乘
正
从
刘徽
舌
踵
虚
盈
虚
盈
(32+36)×32÷2
制作这个椅子面需要多少平方厘米的木材?
=68×32÷2
=2176÷2
=1088(平方厘米)
答:制作这个椅子面需要1088平方厘米的木材。
梯形的面积=(上底+下底)×高÷2
梯形的面积=(上底+下底)×(高÷2)
梯形的面积=(上底+下底)÷2×高
= 每行面积单位的个数 × 行数
×
面积单位的总个数
S = a
S = a
h
h ÷ 2
S =(a+b) h ÷ 2
=
1.春秋兽面纹牌,为地方玉制成,玉料呈青
灰色,局部有深褐色浸斑,半透明。体扁平,
作倒梯形,上底约7厘米,下底约8厘米,高
约6厘米,这块春秋兽面纹牌的牌面面积大
约是多少平方厘米?
7+8)×6÷2
=15×6÷2
=90÷2
=45(平方厘米)
答:牌面面积大约是45平方厘米。
C.平行四边形的面积最大
2.哪种说法正确?
B.梯形的面积最大
D.三种图形的面积一样大
=5×
A.三角形的面积最大
=5×高
三角形面积=10×高÷2 =5×高
梯形面积=(4+6)×高÷2 =5×高
平行四边形的面积=5×高
D
)。
当堂检测:
1.比较右面三个图形面积的大小,我们发现(
A.三角形的面积最大
B.梯形的面积最大
C.一样大
2.王大伯用45米长的篱笆在河边围了一块高为20米的直角梯形
菜园(如图,河岸不围篱笆),这块菜园的面积是多少平方米
必做作业:
课本74页自主练习第3、4题。
选做作业:
一个加工厂运来一批钢管。把它堆成梯形形状,最高层
有10根,最下层有18根。每相邻两层都相差1根,这对钢管
共有多少根
梯形的面积
【教学目标】
1.在自主探索、合作交流中经历梯形面积公式的推导过程,掌握梯形面积的计算方法,并能灵活运用公式解决相关的数学问题。
2.通过猜想、验证、实践等数学活动,发展空间观念和推理能力,获得解决问题的多种策略,感受数学方法的内在魅力。
3.通过探索活动,激发学习兴趣、培养严谨、科学的学习态度、勇于探索、乐于合作的精神。
【教学重点】理解并掌握梯形面积计算公式。
【教学难点】理解平行四边形的面积计算公式的推导过程。
制作这个椅子面需要多少平方厘米的木材?
上底32厘米,
下底36厘米,
高32厘米。
1.试一试:借助学具剪一剪、拼一拼,自主探究梯形的面
积公式。
2.说一说:小组交流,把探究的过程互相说一说。
探究提示
箕
田
术
曰
并
踵
舌
而
半
之
以
乘
正
从
箕
田
术
曰
并
踵
舌
而
半
之
以
乘
正
从
刘徽
舌
踵
虚
盈
虚
盈
(32+36)×32÷2
制作这个椅子面需要多少平方厘米的木材?
=68×32÷2
=2176÷2
=1088(平方厘米)
答:制作这个椅子面需要1088平方厘米的木材。
梯形的面积=(上底+下底)×高÷2
梯形的面积=(上底+下底)×(高÷2)
梯形的面积=(上底+下底)÷2×高
= 每行面积单位的个数 × 行数
×
面积单位的总个数
S = a
S = a
h
h ÷ 2
S =(a+b) h ÷ 2
=
1.春秋兽面纹牌,为地方玉制成,玉料呈青
灰色,局部有深褐色浸斑,半透明。体扁平,
作倒梯形,上底约7厘米,下底约8厘米,高
约6厘米,这块春秋兽面纹牌的牌面面积大
约是多少平方厘米?
7+8)×6÷2
=15×6÷2
=90÷2
=45(平方厘米)
答:牌面面积大约是45平方厘米。
C.平行四边形的面积最大
2.哪种说法正确?
B.梯形的面积最大
D.三种图形的面积一样大
=5×
A.三角形的面积最大
=5×高
三角形面积=10×高÷2 =5×高
梯形面积=(4+6)×高÷2 =5×高
平行四边形的面积=5×高
D
)。
当堂检测:
1.比较右面三个图形面积的大小,我们发现(
A.三角形的面积最大
B.梯形的面积最大
C.一样大
2.王大伯用45米长的篱笆在河边围了一块高为20米的直角梯形
菜园(如图,河岸不围篱笆),这块菜园的面积是多少平方米
必做作业:
课本74页自主练习第3、4题。
选做作业:
一个加工厂运来一批钢管。把它堆成梯形形状,最高层
有10根,最下层有18根。每相邻两层都相差1根,这对钢管
共有多少根
