2025年中考压轴题型解析 题型二 填空压轴题 课件(共61张PPT)
文档属性
| 名称 | 2025年中考压轴题型解析 题型二 填空压轴题 课件(共61张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 00:00:00 | ||
图片预览








文档简介
(共61张PPT)
题型二
填空压轴题
2025年中考题型解析
类型1 几何双空题
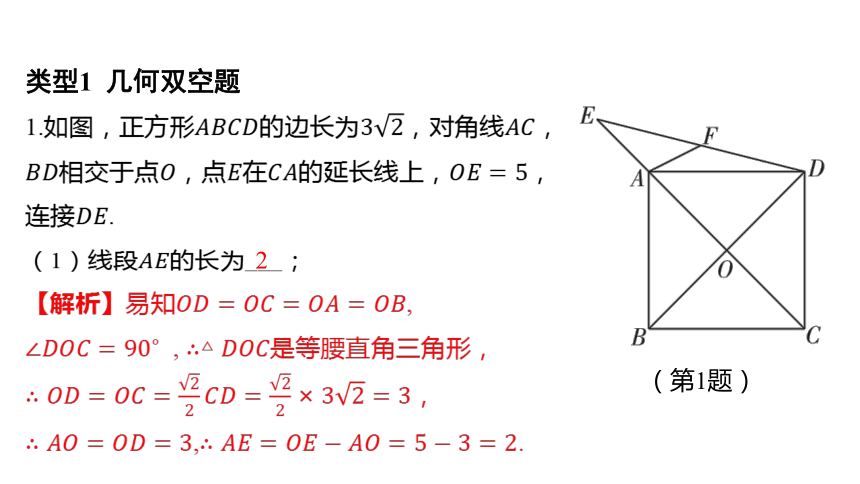
(第1题)
1.如图,正方形的边长为,对角线 ,
相交于点,点在的延长线上, ,
连接 .
(1)线段 的长为___;
2
【解析】易知 ,
, 是等腰直角三角形,
,
, .
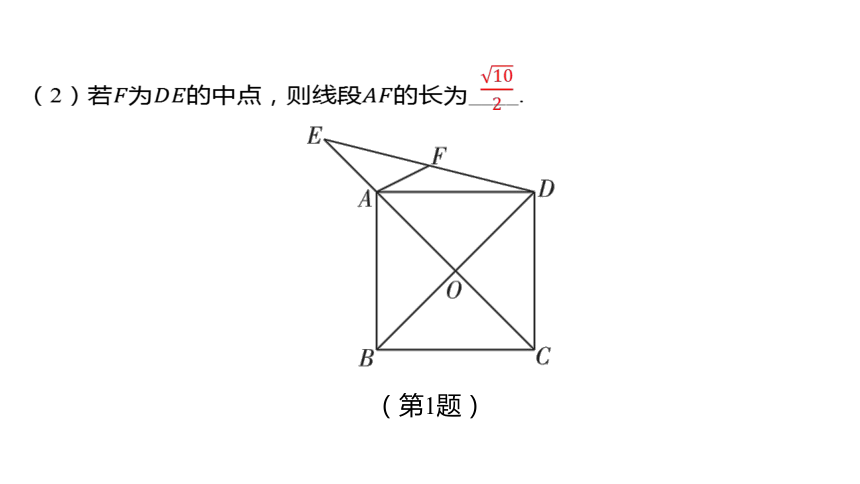
(2)若为的中点,则线段 的长为_ ___.
(第1题)
【解析】如图,延长到点,使得,连接,过点 作
,垂足为.在中, ,
, ,
. 点为的中点,点为的中点,
为的中位线, (依据:三角形的中位线定理).
. .
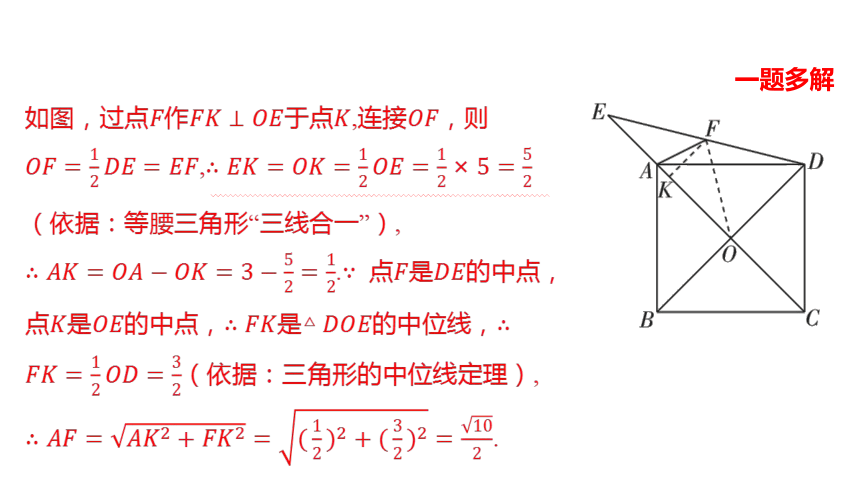
一题多解
如图,过点作于点,连接 ,则
,
(依据:等腰三角形“三线合一”),
. 点是 的中点,
点是的中点,是的中位线,
(依据:三角形的中位线定理),
.
. .
(第2题)
2.如图,在四边形中, ,
,,延长至点 ,使得
,连接 .
(1)____ ;
45
(第2题)
【解析】如图,连接.设 ,与 交于
点 ,, 垂直平分线
段, ,
,
,
,
, .
(2)若,,则 的长为_________.
(第2题)
(第2题)
【解析】,.连接 ,如图,则
, , 是等
腰直角三角形, ,
,
.
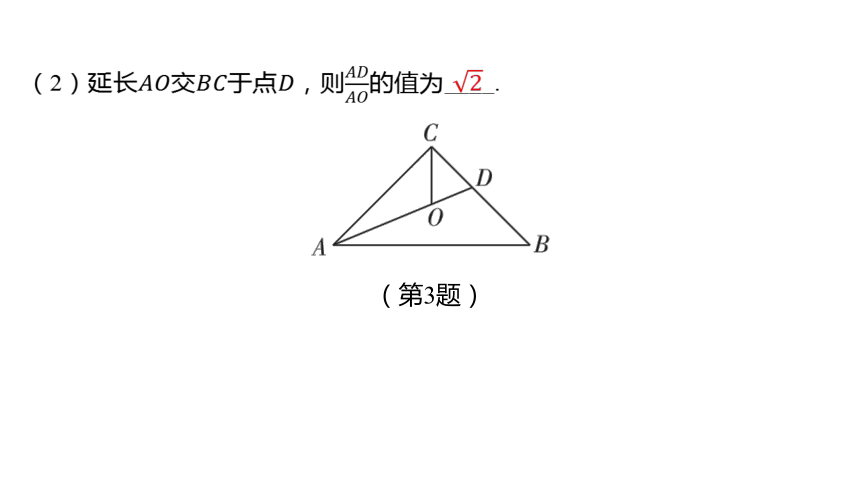
(第3题)
3.如图,在中,, ,
和的平分线相交于点 .
(1)______ ;
112.5
【解析】 是等腰直角三角形,
, 平分,平分 ,
, ,
.
(2)延长交于点,则 的值为____.
(第3题)
(第3题)
【解析】如图,过点作,交 的延长线
于点, , , .
,
,
,, .
,, .
4.如图,在边长为2的正六边形中,连接 .
(第4题)
(第4题)
(1)____ ;
30
【解析】 ,
, .
(2)点为的中点,连接,交于点,则 _ ___.
(第4题)
【解析】如图,延长,交于点 ,延长
,交于点,易得 为等边三角
形,, 点
为的中点,, .
易证, ,
.易证,.易得 ,
.
5.如图(1),在三角形纸片中, ,折叠三角形纸片,使得点
与点重合,展开后得到折痕,再次折叠纸片,使得点与点 重合,
展开后得到折痕,折痕与交于点,连接, ,如图(2).
(第5题)
(1)若 ,则____ .
20
(第5题)
【解析】如图(1),连接,由折叠可知点是的中点,点是 的
中点,是的中位线,, ,
, .易知 ,
,,,, 四点共圆,
.
(2)若,,则 的值是____.
(第5题)
【解析】,, ,
,, .易证
,,即 ,
,, ,
.易证 ,
,即, ,
,.易知 ,
,.如图(2),过点 作
于点,则 (提示:三角形
面积公式), ,
.
. .
6.如图,在菱形中, ,,点为对角线
上一动点,连接 .
(第6题)
(1)当时, ______;
图(1)
【解析】在菱形中, ,
, .若
,如图(1),则
,
,
,
.
(2)延长到点,使得,连接,当 的周长最小时,
____.
12
(第6题)
【解析】如图(2),在上截取,连接 ,
,,.又 ,
, (依据:相似三角形的周长之
比等于相似比), 当的周长最小时, 的周长也最小.易知
,的周长为, 当点
,,共线时, 的周长最小(提示:两点之间线段最短),如图
(3).
. .
. .
. .
,,.易得 ,
.
图(2)
图(3)
7.如图,在矩形中,点在上,连接 ,
将绕点逆时针旋转,得到,点 正好
落在上的点处,连接,延长交于点 ,
连接 .
(1)若,则 的长为_________;
【解析】由旋转可得, ,
, , 是
等腰直角三角形., ,
, .
(2) 的值是_______.
【解析】易得 ,
.易证 ,
, .由旋转的性质得,
,
, ,
,, 点为的中点,,
(点拨:直角三角形斜边上的中线等于斜边的一
半), ,
.
. .
8.将一张正方形纸片(如图①)按如图所示方式折叠得到一只小猫,已知图
⑤中 , .
(1)图③中____ ;
30
【解析】如图,过点作于点 ,由题可知
,由对称性易知
.
(2)该正方形纸片的边长为_________.
【解析】易知在中,,.
在 中,,,
,即正方形纸片的对角线长为,
易得正方形纸片的边长为 .
9.如图,标号为①,②,③,④的矩形不重叠地围成
矩形 ,已知矩形①和矩形②能够重合,矩形③
和矩形④能够重合,这四个矩形的面积都是5,
,,且 .
(1)若,是整数,则 的长是___;
4
【解析】分析易得 矩形①和矩形③的面积都是5,, 是整
数,且,,, 的长为4.
(2)若代数式的值为零,则 的值是_________.
【解析】由题意知,
,
或 ,即
(不符合题意,舍去)或 矩形①和矩形③的
面积都是5,,,,, ,
,
,, .
类型2 函数双空题
(第10题)
10.如图,在平面直角坐标系中,直线与
轴、轴分别交于点,,直线与 相交于点
.已知直线与轴交于点 .
(1)若的中点恰好落在轴上,则 的面积为___;
3
【解析】如图,过点作轴于点 ,则
.又, ,
, 点在直线上, ,
,,.将, 分
别代入,得解得 直线 的
解析式为.令,得 ;令
,解得 ,
.
(第10题)
(2)若,则 的取值范围为____________.
【解析】易知.又,, 点是 的中点.
易知当时,点与点或点重合,可知当点 在线
段上运动时,.易得当点与点重合时, ,
当点与点重合时, .利用数形结合思想分析可知,
若,则 .
(第11题)
11.如图,在平面直角坐标系中,已知直线
和直线,点 是直
线上一点,过点作轴的垂线交于点
(1) __.
【解析】当时,, ,
故 .
(第11题)
(2)过点作轴的垂线交于点,过点作
轴的垂线交于点,过点作轴的垂线交 于
点,过点作轴的垂线交于点 依次进
行下去,则点 的横坐标为________.
【解析】由题意可知, ,
,,, ,
, 的横坐标为
, 点的横坐标为 .
(第12题)
12.如图,在平面直角坐标系中,经过坐标原点
的直线与反比例函数的图象交于 ,
两点,点在反比例函数 的
图象上.
(1) 的值为_____;
【解析】, 关于原点对称,则
, ,由题意可知
, .
(2)若,,则 的值为____.
(第12题)
【解析】如图,连接 .由反比例函数的中心对
称性可知,又, .
过点作轴于点,过点作 轴于
点,易证, ,
由可设, ,则
,, .设点
的坐标为,则, ,
,, ,
, .
(第13题)
13.如图,在平面直角坐标系中,正方形 的顶
点在直线上,轴,已知,点
的横坐标为9,双曲线与正方形
有交点.
(1)若双曲线经过点,则 ___;
9
【解析】轴,,点 的横坐标为9,
点的横坐标为3.又点在直线上, 点 的
坐标为, .
(第13题)
(2)若双曲线与正方形 有两个
公共点,则 的取值范围为___________.
【解析】轴,, 点 的纵坐标为
,轴. ,点
, 点的坐标为 .当双曲线
经过点时, ;当双曲线
经过点时,.故的取值范围为 .
(第14题)
14.如图,等边三角形的边, 分别与反比例
函数的图象交于点,,点在 轴的
负半轴上.已知点的横坐标为
(1) 的值为_______;
【解析】由题意易知点的纵坐标为 ,
点的坐标为 .
(2) 的值为____.
12
(第14题)
【解析】如图,过点作轴于点,过点 作
于点,易得 .
15.在平面直角坐标系中,点为坐标原点,已知抛物线
(其中为常数)的顶点为 .
(1)设点到轴的距离为,则 的最小值为___;
4
【解析】是抛物线 的顶点,
,, 的最小值为4.
(2)若直线与抛物线交于, 两点,且
,则当时, 的取值范围是____________.
【解析】易知 ,
点,在直线 上,
, 点,关于点对称,
(突破点:根据题干条件,用含
的式子表示出点的坐标). 点 在
. .
抛物线 上(关键点),
,解得 .
当时,, ,如图(1),
观察图象可知当 ,即抛物线在直线下方
时,.当时, ,
,如图(2),观察图象可知当 ,
即抛物线在直线下方时, .综上可知,
当时,的取值范围是 .
16.在平面直角坐标系中,点,, 在抛物线
上.
(1)若, ,则该抛物线的表达式为____________;
【解析】,,, 抛物线的对称轴是直线
,,, 在该抛物
线上,,,,, 该抛物线的表达式为
.
(2)已知抛物线的对称轴为直线,若,则 的取值范
围为__________.
【解析】对于,当 时,
, 该抛物线经过原点.分两种情况讨论.
①当 时,抛物线开口向上.
, 点在轴下方,点,
在轴上方,且点,中,点 距抛物线的对称
轴较近,如图. 点在 轴上方,
. 点,中,点 距抛物线的对称
轴较近,的中点在直线 左侧,
,当 时,抛
物线开口向下,若,则 ,与
题中条件矛盾;若,则 ,与题中条
件矛盾;若, ,与题中条件矛
盾.故此种情况不存在.综上所述, 的取值范围
为 .
17.点是直线上一点且位于第一象限,过点作轴与
轴的垂线,垂线与坐标轴围成的矩形周长为8.
(1) ___;
4
【解析】设点,则, .
(2)抛物线与直线 只有一个有
公共点时,则 的取值范围为_________________.
或
【解析】对于,当时,,当时, .对于
,当时,,当时,, 当
时,抛物线 与直线有1个公共点.
,整理,得,令 ,即
,解得 ,此时,抛物线
与直线的交点为 ,符合题意,
综上所述,当抛物线 与直线只有一个公共点
时,的取值范围是或 .
(第18题)
18.如图,反比例函数 的图象过点
,,轴于点 ,二次函数
的图象过点,顶点为 .
(1)若点的横坐标为,请用含 的式子表示
点 的纵坐标:______.
【解析】由题意知,, 点 的坐标
为,,即 点 的横坐
标为,即, 点的纵坐标为 .
(2)当值变化时, 的最小值为_ _____.
(第18题)
【解析】由(1)可知,点 在直线
上,且在轴左侧.如图,作点
关于直线的对称点,连接
交直线于点,此时 的
值最小,最小值为的长. 点, 在反
比例函数的图象上,, 解得,, .
易得 ,
,即
的最小值为 .
感谢观看
题型二
填空压轴题
2025年中考题型解析
类型1 几何双空题
(第1题)
1.如图,正方形的边长为,对角线 ,
相交于点,点在的延长线上, ,
连接 .
(1)线段 的长为___;
2
【解析】易知 ,
, 是等腰直角三角形,
,
, .
(2)若为的中点,则线段 的长为_ ___.
(第1题)
【解析】如图,延长到点,使得,连接,过点 作
,垂足为.在中, ,
, ,
. 点为的中点,点为的中点,
为的中位线, (依据:三角形的中位线定理).
. .
一题多解
如图,过点作于点,连接 ,则
,
(依据:等腰三角形“三线合一”),
. 点是 的中点,
点是的中点,是的中位线,
(依据:三角形的中位线定理),
.
. .
(第2题)
2.如图,在四边形中, ,
,,延长至点 ,使得
,连接 .
(1)____ ;
45
(第2题)
【解析】如图,连接.设 ,与 交于
点 ,, 垂直平分线
段, ,
,
,
,
, .
(2)若,,则 的长为_________.
(第2题)
(第2题)
【解析】,.连接 ,如图,则
, , 是等
腰直角三角形, ,
,
.
(第3题)
3.如图,在中,, ,
和的平分线相交于点 .
(1)______ ;
112.5
【解析】 是等腰直角三角形,
, 平分,平分 ,
, ,
.
(2)延长交于点,则 的值为____.
(第3题)
(第3题)
【解析】如图,过点作,交 的延长线
于点, , , .
,
,
,, .
,, .
4.如图,在边长为2的正六边形中,连接 .
(第4题)
(第4题)
(1)____ ;
30
【解析】 ,
, .
(2)点为的中点,连接,交于点,则 _ ___.
(第4题)
【解析】如图,延长,交于点 ,延长
,交于点,易得 为等边三角
形,, 点
为的中点,, .
易证, ,
.易证,.易得 ,
.
5.如图(1),在三角形纸片中, ,折叠三角形纸片,使得点
与点重合,展开后得到折痕,再次折叠纸片,使得点与点 重合,
展开后得到折痕,折痕与交于点,连接, ,如图(2).
(第5题)
(1)若 ,则____ .
20
(第5题)
【解析】如图(1),连接,由折叠可知点是的中点,点是 的
中点,是的中位线,, ,
, .易知 ,
,,,, 四点共圆,
.
(2)若,,则 的值是____.
(第5题)
【解析】,, ,
,, .易证
,,即 ,
,, ,
.易证 ,
,即, ,
,.易知 ,
,.如图(2),过点 作
于点,则 (提示:三角形
面积公式), ,
.
. .
6.如图,在菱形中, ,,点为对角线
上一动点,连接 .
(第6题)
(1)当时, ______;
图(1)
【解析】在菱形中, ,
, .若
,如图(1),则
,
,
,
.
(2)延长到点,使得,连接,当 的周长最小时,
____.
12
(第6题)
【解析】如图(2),在上截取,连接 ,
,,.又 ,
, (依据:相似三角形的周长之
比等于相似比), 当的周长最小时, 的周长也最小.易知
,的周长为, 当点
,,共线时, 的周长最小(提示:两点之间线段最短),如图
(3).
. .
. .
. .
,,.易得 ,
.
图(2)
图(3)
7.如图,在矩形中,点在上,连接 ,
将绕点逆时针旋转,得到,点 正好
落在上的点处,连接,延长交于点 ,
连接 .
(1)若,则 的长为_________;
【解析】由旋转可得, ,
, , 是
等腰直角三角形., ,
, .
(2) 的值是_______.
【解析】易得 ,
.易证 ,
, .由旋转的性质得,
,
, ,
,, 点为的中点,,
(点拨:直角三角形斜边上的中线等于斜边的一
半), ,
.
. .
8.将一张正方形纸片(如图①)按如图所示方式折叠得到一只小猫,已知图
⑤中 , .
(1)图③中____ ;
30
【解析】如图,过点作于点 ,由题可知
,由对称性易知
.
(2)该正方形纸片的边长为_________.
【解析】易知在中,,.
在 中,,,
,即正方形纸片的对角线长为,
易得正方形纸片的边长为 .
9.如图,标号为①,②,③,④的矩形不重叠地围成
矩形 ,已知矩形①和矩形②能够重合,矩形③
和矩形④能够重合,这四个矩形的面积都是5,
,,且 .
(1)若,是整数,则 的长是___;
4
【解析】分析易得 矩形①和矩形③的面积都是5,, 是整
数,且,,, 的长为4.
(2)若代数式的值为零,则 的值是_________.
【解析】由题意知,
,
或 ,即
(不符合题意,舍去)或 矩形①和矩形③的
面积都是5,,,,, ,
,
,, .
类型2 函数双空题
(第10题)
10.如图,在平面直角坐标系中,直线与
轴、轴分别交于点,,直线与 相交于点
.已知直线与轴交于点 .
(1)若的中点恰好落在轴上,则 的面积为___;
3
【解析】如图,过点作轴于点 ,则
.又, ,
, 点在直线上, ,
,,.将, 分
别代入,得解得 直线 的
解析式为.令,得 ;令
,解得 ,
.
(第10题)
(2)若,则 的取值范围为____________.
【解析】易知.又,, 点是 的中点.
易知当时,点与点或点重合,可知当点 在线
段上运动时,.易得当点与点重合时, ,
当点与点重合时, .利用数形结合思想分析可知,
若,则 .
(第11题)
11.如图,在平面直角坐标系中,已知直线
和直线,点 是直
线上一点,过点作轴的垂线交于点
(1) __.
【解析】当时,, ,
故 .
(第11题)
(2)过点作轴的垂线交于点,过点作
轴的垂线交于点,过点作轴的垂线交 于
点,过点作轴的垂线交于点 依次进
行下去,则点 的横坐标为________.
【解析】由题意可知, ,
,,, ,
, 的横坐标为
, 点的横坐标为 .
(第12题)
12.如图,在平面直角坐标系中,经过坐标原点
的直线与反比例函数的图象交于 ,
两点,点在反比例函数 的
图象上.
(1) 的值为_____;
【解析】, 关于原点对称,则
, ,由题意可知
, .
(2)若,,则 的值为____.
(第12题)
【解析】如图,连接 .由反比例函数的中心对
称性可知,又, .
过点作轴于点,过点作 轴于
点,易证, ,
由可设, ,则
,, .设点
的坐标为,则, ,
,, ,
, .
(第13题)
13.如图,在平面直角坐标系中,正方形 的顶
点在直线上,轴,已知,点
的横坐标为9,双曲线与正方形
有交点.
(1)若双曲线经过点,则 ___;
9
【解析】轴,,点 的横坐标为9,
点的横坐标为3.又点在直线上, 点 的
坐标为, .
(第13题)
(2)若双曲线与正方形 有两个
公共点,则 的取值范围为___________.
【解析】轴,, 点 的纵坐标为
,轴. ,点
, 点的坐标为 .当双曲线
经过点时, ;当双曲线
经过点时,.故的取值范围为 .
(第14题)
14.如图,等边三角形的边, 分别与反比例
函数的图象交于点,,点在 轴的
负半轴上.已知点的横坐标为
(1) 的值为_______;
【解析】由题意易知点的纵坐标为 ,
点的坐标为 .
(2) 的值为____.
12
(第14题)
【解析】如图,过点作轴于点,过点 作
于点,易得 .
15.在平面直角坐标系中,点为坐标原点,已知抛物线
(其中为常数)的顶点为 .
(1)设点到轴的距离为,则 的最小值为___;
4
【解析】是抛物线 的顶点,
,, 的最小值为4.
(2)若直线与抛物线交于, 两点,且
,则当时, 的取值范围是____________.
【解析】易知 ,
点,在直线 上,
, 点,关于点对称,
(突破点:根据题干条件,用含
的式子表示出点的坐标). 点 在
. .
抛物线 上(关键点),
,解得 .
当时,, ,如图(1),
观察图象可知当 ,即抛物线在直线下方
时,.当时, ,
,如图(2),观察图象可知当 ,
即抛物线在直线下方时, .综上可知,
当时,的取值范围是 .
16.在平面直角坐标系中,点,, 在抛物线
上.
(1)若, ,则该抛物线的表达式为____________;
【解析】,,, 抛物线的对称轴是直线
,,, 在该抛物
线上,,,,, 该抛物线的表达式为
.
(2)已知抛物线的对称轴为直线,若,则 的取值范
围为__________.
【解析】对于,当 时,
, 该抛物线经过原点.分两种情况讨论.
①当 时,抛物线开口向上.
, 点在轴下方,点,
在轴上方,且点,中,点 距抛物线的对称
轴较近,如图. 点在 轴上方,
. 点,中,点 距抛物线的对称
轴较近,的中点在直线 左侧,
,当 时,抛
物线开口向下,若,则 ,与
题中条件矛盾;若,则 ,与题中条
件矛盾;若, ,与题中条件矛
盾.故此种情况不存在.综上所述, 的取值范围
为 .
17.点是直线上一点且位于第一象限,过点作轴与
轴的垂线,垂线与坐标轴围成的矩形周长为8.
(1) ___;
4
【解析】设点,则, .
(2)抛物线与直线 只有一个有
公共点时,则 的取值范围为_________________.
或
【解析】对于,当时,,当时, .对于
,当时,,当时,, 当
时,抛物线 与直线有1个公共点.
,整理,得,令 ,即
,解得 ,此时,抛物线
与直线的交点为 ,符合题意,
综上所述,当抛物线 与直线只有一个公共点
时,的取值范围是或 .
(第18题)
18.如图,反比例函数 的图象过点
,,轴于点 ,二次函数
的图象过点,顶点为 .
(1)若点的横坐标为,请用含 的式子表示
点 的纵坐标:______.
【解析】由题意知,, 点 的坐标
为,,即 点 的横坐
标为,即, 点的纵坐标为 .
(2)当值变化时, 的最小值为_ _____.
(第18题)
【解析】由(1)可知,点 在直线
上,且在轴左侧.如图,作点
关于直线的对称点,连接
交直线于点,此时 的
值最小,最小值为的长. 点, 在反
比例函数的图象上,, 解得,, .
易得 ,
,即
的最小值为 .
感谢观看
同课章节目录
