2025年中考压轴题型解析 题型五 几何探究题 课件(共66张PPT)
文档属性
| 名称 | 2025年中考压轴题型解析 题型五 几何探究题 课件(共66张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 00:00:00 | ||
图片预览






文档简介
(共66张PPT)
题型五
几何探究题
2025年中考题型解析
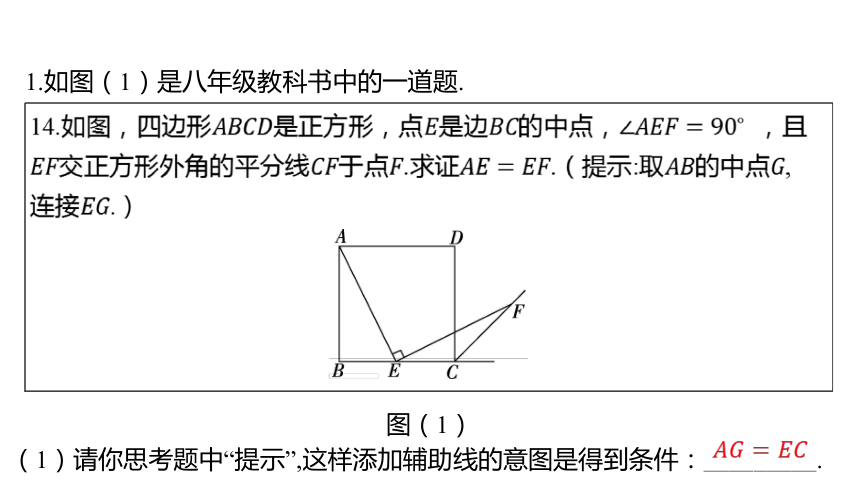
1.如图(1)是八年级教科书中的一道题.
14.如图,四边形是正方形,点是边的中点, ,且
交正方形外角的平分线于点.求证.(提示:取的中点 ,
连接 .)
__________________________________________________
图(1)
(1)请你思考题中“提示”,这样添加辅助线的意图是得到条件:_________.
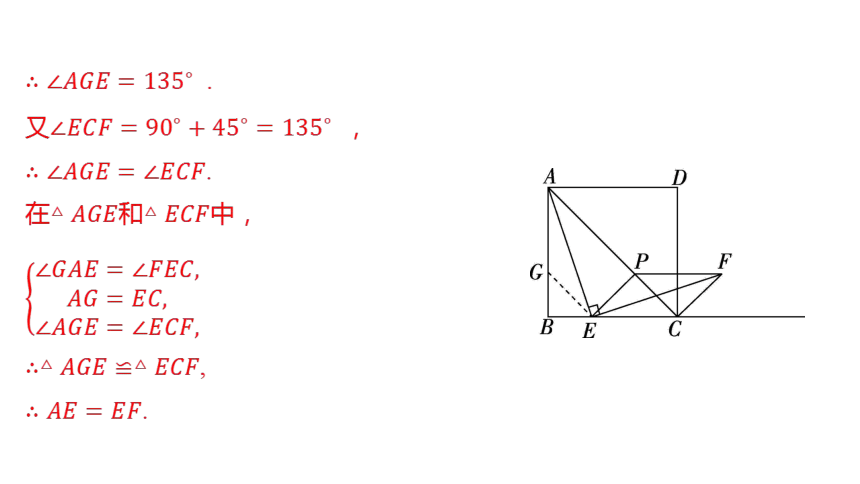
(2)如图(2),若点是边上任意一点(不与点, 重合),其他条件不
变.求证: .
证明:在上取点,使 .
四边形是正方形, , ,
.
, ,
.
,, ,
图(2)
.
又 ,
.
在和 中,
,
.
(3)在(2)的条件下,连接,过点作,垂足为.设,当 为
何值时,四边形 是平行四边形?并给予证明.
【答案】当时,四边形 是平行四边形.
证明:如图,在上取点,使 .
设正方形的边长为1,则由,得 ,
,, .
由(2)得, .
四边形 是平行四边形,
.
由易得 是等腰直角三角形,
,即 ,
.
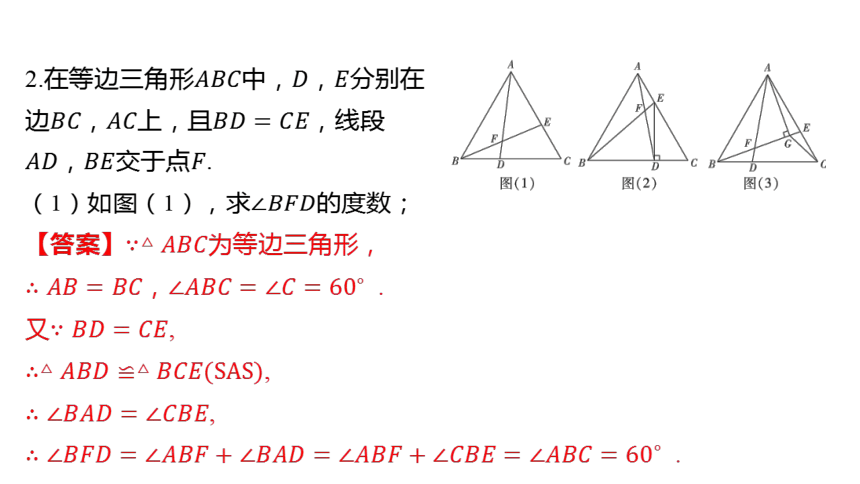
2.在等边三角形中,, 分别在
边,上,且 ,线段
,交于点 .
(1)如图(1),求 的度数;
【答案】 为等边三角形,
, .
又 ,
,
,
.
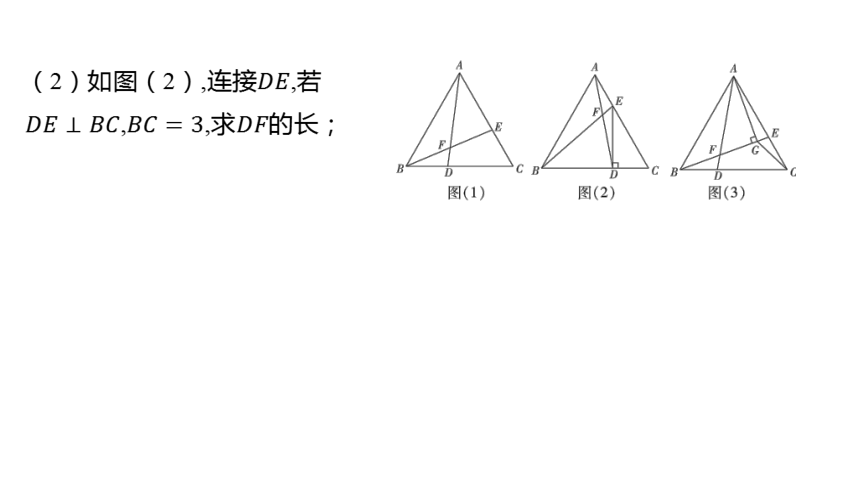
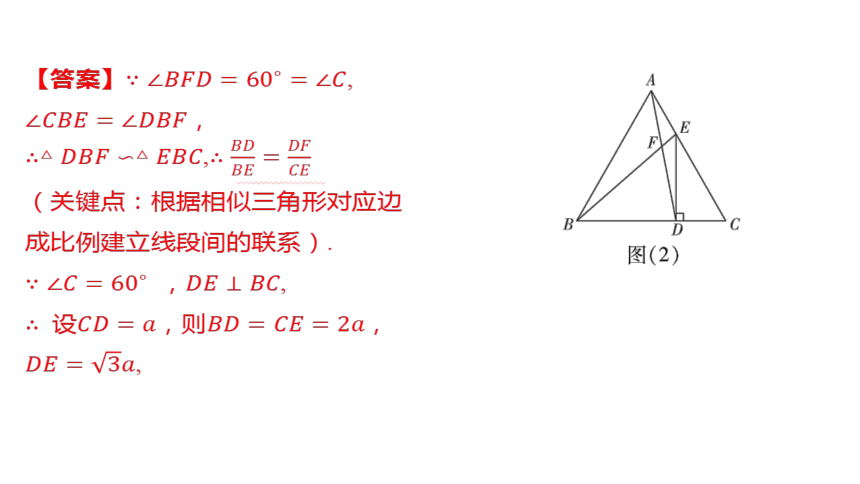
(2)如图(2),连接 ,若
,,求 的长;
【答案】 ,
,
,
(关键点:根据相似三角形对应边
成比例建立线段间的联系).
, ,
设,则 ,
,
. .
, ,
, ,
,
, .
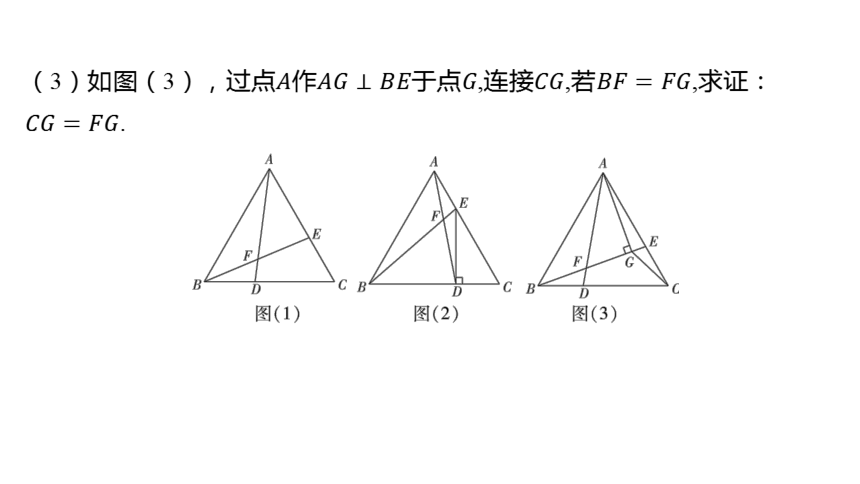
(3)如图(3),过点作于点,连接,若 ,求证:
.
证明:如图,延长到点,使,连接 ,
(点拨:构造等边三角形,转化待证线段).
, ,
是等边三角形(依据:有一个角是 的等腰
三角形是等边三角形),
, ,
.
又,, ,
. .
. .
. .
, ,
.
是等边三角形, ,
.
又,, ,
是等边三角形,
, .
3.为平行四边形内一点,分别连接,, .
(1)如图(1),过点作交于点,延长交于点 .
①若,,求 的长;
【答案】, .
又, .
又 ,
,
.
,, ,
.
②连接,,求证: .
图(1)
证明:如图(1),延长交于点 ,
则四边形和四边形 均是平行四边形,
, .
, .
由(1)知 .
又 ,
.
,
, ,
,
, ,
,
,即 .
(2)如图(2),为平行四边形外一点,连接 并延长,分别交
,于点,,连接.若,, ,
求证: .
证明:如图(2),连接 .
图(2)
, .
又, ,
, .
在上找一点,连接,使得 ,
.
,
, .
, ,
,
,即 .
4.问题背景 如图(1),在矩形中,点,分别是,的中点,连接 ,
,求证: .
证明: 四边形 是矩形,
, .
,分别是, 的中点,
,即 ,
.
问题探究 如图(2),在四边形中,, ,点是 的
中点,点在边上,,与交于点,求证: .
图(1)
证明:如图(1),过点作 于
点,延长,,交于点 ,
则四边形是矩形, ,
.
,, .
, .
又, ,
(提示:“8”字型全
等),
, .
又 ,
,
, ,
.
. .
问题拓展 如图(3),在“问题探究”的条件下,连接,, ,
直接写出 的值.
图(1)
图(2)
图(3)
【答案】 .
图(2)
【解析】解法提示:如图(2),延长, ,
交于点,过点作于点,连接 .
设,则, ,
.
,, .
又是的中点,垂直平分 ,
.
, (提示:“8”字
型相似),
,
, .
. .
5.在中, ,是边上的高,将绕点 顺时针
旋转,得到,点,的对应点分别为, .
图(1)
图(2)
图(3)
(1)如图(1),若,,分别与,交于点, ,求证:四
边形 是矩形.
证明:是边上的高, .
由旋转的性质得 .
, .
又 ,
四边形 是矩形(依据:有三个角是直角的四边形是矩形).
. .
图(1)
(2)如图(2),若点恰好落在上,点恰好落在上,延长 交
于点,连接,求 的度数.
【答案】如图,过点分别作于点,
于点 .
由旋转可得 .
又 ,
图(2)
,
.
,
, ,
,
.
又, ,
点在 的平分线上(依据:到一个角的两边距离相等的点,在这个
角的平分线上),
.
. .
(3)如图(3),若,与交于点,, ,求
的面积.
【答案】在中, .
易证 ,
,
, .
,
图(3)
.
又 ,
,
.
又 , ,
,
,
,
点是 的中点,
.
图(3)
6.如图,点为正方形的边上一点(不与点,重合),以 为边
在正方形外作正方形,的延长线交对角线于点 .
图(1)
图(2)
图(3)
(1)如图(1),连接,,写出四边形 的形状,并说明理由.
【答案】四边形 是平行四边形.
理由: 四边形和四边形 都是正方形,
, ,
, ,
, ,
, ,
,即 ,
四边形 是平行四边形.
图(1)
(2)如图(2),过点作于点,连接, ,求证:
.
证明:由题意知 ,
四边形 是矩形,
,, .
由正方形的性质,可知 ,
,
,
图(2)
,
.
,
,
.
图(2)
(3)如图(3),若的延长线恰好经过点,求 的值.
【答案】如图,过点作于点,
则 .
由(2)得 .
设,则 .
图(3)
点不与, 重合,
.
易知, ,
, ,
,
,即 ,
,
解得 (负值已舍去,结果已检验),
.
7.如图(1),四边形是菱形, ,点是上一动点,点
是对角线延长线上一点,且,连接,,交于点 .
图(1)
图(2)
(1)求 的度数.
【答案】 四边形是菱形, ,
, , ,
,
.
又 ,
,
,
.
图(1)
(2)如图(2),连接,交于点,延长交于点,试判断
与 的数量关系,并加以证明.
【答案】 .
证明:由(1)知, ,
, 是等边三角形,
.
, ,
,
,
,
.
图(2)
(3)在(2)的基础上,若,点为的三等分点,且靠近点 ,
求 的长.
【答案】易得,, ,
.
如图,过点作于点 ,
则, ,
, .
由(2)知 是等边三角形,
.
方法一: ,
, ,
, ,
,, ,
,
.
方法二:如图,过点作,交 的延
长线于点 ,
则 , ,
是等边三角形,
.
,
,
,
.
8.如图,四边形 为正方形,四边形
为矩形,点在边上,点在边
的延长线上,连接,, .
(1)连接,若平分,求 的长.
【答案】平分 ,
.
四边形 为矩形,
,, ,
,
,
,
,
.
在正方形中, .
设,则 ,
.
在中, ,
,
解得,即 .
(2)连接交于点,连接交于点 ,
若 ,
①求 的度数;
【答案】 四边形 为正方形,
, .
在矩形中, ,
四边形 是正方形,
, ,
, ,
, ,
.
又, ,
,
,
,
.
②求 的长.
【答案】方法一:四边形 为正方形,
.
由①知 ,
,
,
.
又 ,
.
又 ,
,
,
又, ,
,
,
.
方法二:延长交于点 .
由①知 .
又 ,
点是 的中点,
, ,
.
易知 ,
, ,
,
,
.
,
.
9.在中,, ,是斜边上的中线, ,
分别是和上的点,于点,连接 .
(1)如图(1),若平分,求 的度数.
【答案】 ,
, 是斜
边 上的中线,
, .
又平分, ,
, (依据:等腰三角形“三线合一”),
.
在中,是斜边 上的中线,
,
.
. .
. .
(2)若平分 边,其他条件不变.
(ⅰ)如图(2),求 的值;
【答案】在和 中,
,
.
过点作于点 ,如图.
,平分 边,
是的中位线,则 .
易知 是等腰直角三角形,
.
又 ,
,
,
.
(ⅱ)如图(3),过点作,交于点,设与交于点 ,
求证: .
证明: ,
,,,四点共圆(提示:四点在以 为直径的圆上),
(依据:同弧所对的圆周角相等).
,
(依据:两直线平行,内错角相等),
,
, ,
. .
. .
. .
.
又 ,
,
.
易得 ,
.
, ,
,
.
,
(提示:“8”字型相似),
,
.
名师敲重点
知识积累
常见的相似模型
类型 图示及结论
平行线型(“A”字型,“8” 字型)
若,则 .
类型 图示及结论
斜交型
若,则 .
续表
类型 图示及结论
“一线三等角”型
若 ,
则 .
续表
感谢观看
题型五
几何探究题
2025年中考题型解析
1.如图(1)是八年级教科书中的一道题.
14.如图,四边形是正方形,点是边的中点, ,且
交正方形外角的平分线于点.求证.(提示:取的中点 ,
连接 .)
__________________________________________________
图(1)
(1)请你思考题中“提示”,这样添加辅助线的意图是得到条件:_________.
(2)如图(2),若点是边上任意一点(不与点, 重合),其他条件不
变.求证: .
证明:在上取点,使 .
四边形是正方形, , ,
.
, ,
.
,, ,
图(2)
.
又 ,
.
在和 中,
,
.
(3)在(2)的条件下,连接,过点作,垂足为.设,当 为
何值时,四边形 是平行四边形?并给予证明.
【答案】当时,四边形 是平行四边形.
证明:如图,在上取点,使 .
设正方形的边长为1,则由,得 ,
,, .
由(2)得, .
四边形 是平行四边形,
.
由易得 是等腰直角三角形,
,即 ,
.
2.在等边三角形中,, 分别在
边,上,且 ,线段
,交于点 .
(1)如图(1),求 的度数;
【答案】 为等边三角形,
, .
又 ,
,
,
.
(2)如图(2),连接 ,若
,,求 的长;
【答案】 ,
,
,
(关键点:根据相似三角形对应边
成比例建立线段间的联系).
, ,
设,则 ,
,
. .
, ,
, ,
,
, .
(3)如图(3),过点作于点,连接,若 ,求证:
.
证明:如图,延长到点,使,连接 ,
(点拨:构造等边三角形,转化待证线段).
, ,
是等边三角形(依据:有一个角是 的等腰
三角形是等边三角形),
, ,
.
又,, ,
. .
. .
. .
, ,
.
是等边三角形, ,
.
又,, ,
是等边三角形,
, .
3.为平行四边形内一点,分别连接,, .
(1)如图(1),过点作交于点,延长交于点 .
①若,,求 的长;
【答案】, .
又, .
又 ,
,
.
,, ,
.
②连接,,求证: .
图(1)
证明:如图(1),延长交于点 ,
则四边形和四边形 均是平行四边形,
, .
, .
由(1)知 .
又 ,
.
,
, ,
,
, ,
,
,即 .
(2)如图(2),为平行四边形外一点,连接 并延长,分别交
,于点,,连接.若,, ,
求证: .
证明:如图(2),连接 .
图(2)
, .
又, ,
, .
在上找一点,连接,使得 ,
.
,
, .
, ,
,
,即 .
4.问题背景 如图(1),在矩形中,点,分别是,的中点,连接 ,
,求证: .
证明: 四边形 是矩形,
, .
,分别是, 的中点,
,即 ,
.
问题探究 如图(2),在四边形中,, ,点是 的
中点,点在边上,,与交于点,求证: .
图(1)
证明:如图(1),过点作 于
点,延长,,交于点 ,
则四边形是矩形, ,
.
,, .
, .
又, ,
(提示:“8”字型全
等),
, .
又 ,
,
, ,
.
. .
问题拓展 如图(3),在“问题探究”的条件下,连接,, ,
直接写出 的值.
图(1)
图(2)
图(3)
【答案】 .
图(2)
【解析】解法提示:如图(2),延长, ,
交于点,过点作于点,连接 .
设,则, ,
.
,, .
又是的中点,垂直平分 ,
.
, (提示:“8”字
型相似),
,
, .
. .
5.在中, ,是边上的高,将绕点 顺时针
旋转,得到,点,的对应点分别为, .
图(1)
图(2)
图(3)
(1)如图(1),若,,分别与,交于点, ,求证:四
边形 是矩形.
证明:是边上的高, .
由旋转的性质得 .
, .
又 ,
四边形 是矩形(依据:有三个角是直角的四边形是矩形).
. .
图(1)
(2)如图(2),若点恰好落在上,点恰好落在上,延长 交
于点,连接,求 的度数.
【答案】如图,过点分别作于点,
于点 .
由旋转可得 .
又 ,
图(2)
,
.
,
, ,
,
.
又, ,
点在 的平分线上(依据:到一个角的两边距离相等的点,在这个
角的平分线上),
.
. .
(3)如图(3),若,与交于点,, ,求
的面积.
【答案】在中, .
易证 ,
,
, .
,
图(3)
.
又 ,
,
.
又 , ,
,
,
,
点是 的中点,
.
图(3)
6.如图,点为正方形的边上一点(不与点,重合),以 为边
在正方形外作正方形,的延长线交对角线于点 .
图(1)
图(2)
图(3)
(1)如图(1),连接,,写出四边形 的形状,并说明理由.
【答案】四边形 是平行四边形.
理由: 四边形和四边形 都是正方形,
, ,
, ,
, ,
, ,
,即 ,
四边形 是平行四边形.
图(1)
(2)如图(2),过点作于点,连接, ,求证:
.
证明:由题意知 ,
四边形 是矩形,
,, .
由正方形的性质,可知 ,
,
,
图(2)
,
.
,
,
.
图(2)
(3)如图(3),若的延长线恰好经过点,求 的值.
【答案】如图,过点作于点,
则 .
由(2)得 .
设,则 .
图(3)
点不与, 重合,
.
易知, ,
, ,
,
,即 ,
,
解得 (负值已舍去,结果已检验),
.
7.如图(1),四边形是菱形, ,点是上一动点,点
是对角线延长线上一点,且,连接,,交于点 .
图(1)
图(2)
(1)求 的度数.
【答案】 四边形是菱形, ,
, , ,
,
.
又 ,
,
,
.
图(1)
(2)如图(2),连接,交于点,延长交于点,试判断
与 的数量关系,并加以证明.
【答案】 .
证明:由(1)知, ,
, 是等边三角形,
.
, ,
,
,
,
.
图(2)
(3)在(2)的基础上,若,点为的三等分点,且靠近点 ,
求 的长.
【答案】易得,, ,
.
如图,过点作于点 ,
则, ,
, .
由(2)知 是等边三角形,
.
方法一: ,
, ,
, ,
,, ,
,
.
方法二:如图,过点作,交 的延
长线于点 ,
则 , ,
是等边三角形,
.
,
,
,
.
8.如图,四边形 为正方形,四边形
为矩形,点在边上,点在边
的延长线上,连接,, .
(1)连接,若平分,求 的长.
【答案】平分 ,
.
四边形 为矩形,
,, ,
,
,
,
,
.
在正方形中, .
设,则 ,
.
在中, ,
,
解得,即 .
(2)连接交于点,连接交于点 ,
若 ,
①求 的度数;
【答案】 四边形 为正方形,
, .
在矩形中, ,
四边形 是正方形,
, ,
, ,
, ,
.
又, ,
,
,
,
.
②求 的长.
【答案】方法一:四边形 为正方形,
.
由①知 ,
,
,
.
又 ,
.
又 ,
,
,
又, ,
,
,
.
方法二:延长交于点 .
由①知 .
又 ,
点是 的中点,
, ,
.
易知 ,
, ,
,
,
.
,
.
9.在中,, ,是斜边上的中线, ,
分别是和上的点,于点,连接 .
(1)如图(1),若平分,求 的度数.
【答案】 ,
, 是斜
边 上的中线,
, .
又平分, ,
, (依据:等腰三角形“三线合一”),
.
在中,是斜边 上的中线,
,
.
. .
. .
(2)若平分 边,其他条件不变.
(ⅰ)如图(2),求 的值;
【答案】在和 中,
,
.
过点作于点 ,如图.
,平分 边,
是的中位线,则 .
易知 是等腰直角三角形,
.
又 ,
,
,
.
(ⅱ)如图(3),过点作,交于点,设与交于点 ,
求证: .
证明: ,
,,,四点共圆(提示:四点在以 为直径的圆上),
(依据:同弧所对的圆周角相等).
,
(依据:两直线平行,内错角相等),
,
, ,
. .
. .
. .
.
又 ,
,
.
易得 ,
.
, ,
,
.
,
(提示:“8”字型相似),
,
.
名师敲重点
知识积累
常见的相似模型
类型 图示及结论
平行线型(“A”字型,“8” 字型)
若,则 .
类型 图示及结论
斜交型
若,则 .
续表
类型 图示及结论
“一线三等角”型
若 ,
则 .
续表
感谢观看
同课章节目录
