2025年中考数学压轴题型解析 题型六 二次函数实际应用题 课件(共55张PPT)
文档属性
| 名称 | 2025年中考数学压轴题型解析 题型六 二次函数实际应用题 课件(共55张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 16:00:58 | ||
图片预览








文档简介
(共55张PPT)
题型六
二次函数实际应用题
2025年中考题型解析
类型1 抛物线形问题
1.如图,一厂房的顶部为抛物线的一部分,测得两端点,(点, 也
为抛物线上的对称点)之间的距离为,在上距点 处房顶的高
度 .
(1)建立适当的平面直角坐标系,并求出抛物线的表达式.
图(1)
【答案】以线段所在直线为轴,线段的中点
为坐标原点,建立平面直角坐标系如图(1)所示.
,,, .
, ,
.
设抛物线的表达式为 ,
将代入,得 ,
解得 ,
故抛物线的表达式为
.
(2)为了通风需要,房主想利用线段 与抛物线之间的部分建造通风口,
现有两种设计方案:
①建造一个正方形通风口,且面积最大;
②建造两个相同的面积最大的正方形通风口,且两通风口之间的距离为
.
通过计算说明哪种方案通风效果更好(通风口面积越大,通风效果越好.参
考数据: )
图(2)
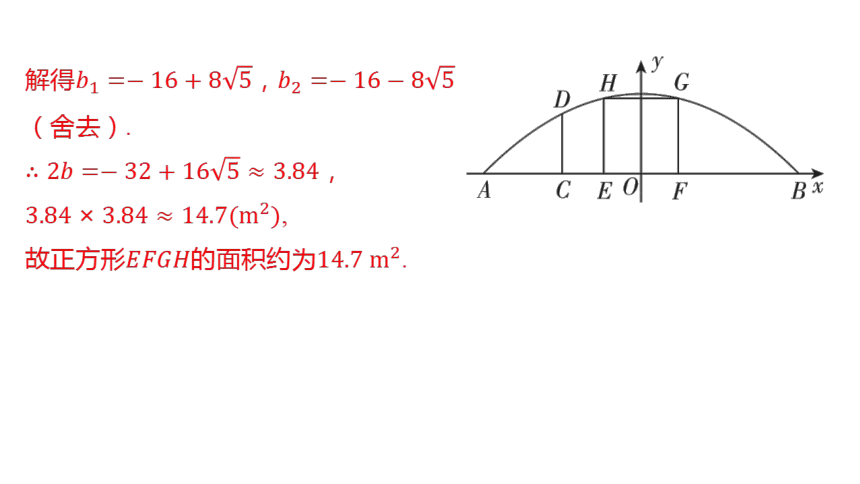
【答案】第①种方案:如图(2),当正
方形通风口的面积最大时,点 ,
在轴上,点, 在抛物线上,且
,
设正方形的边长为 ,
则,代入 ,
得 ,
解得,
(舍去).
,
,
故正方形的面积约为 .
图(3)
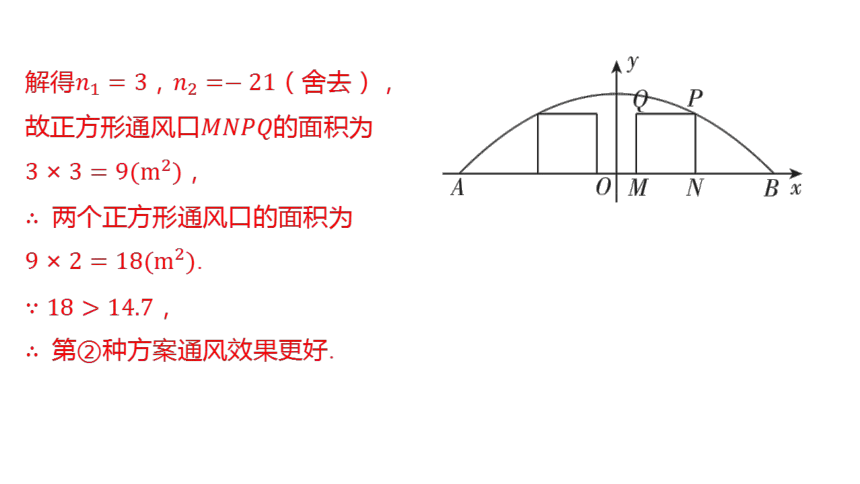
第②种方案:如图(3),当两个相同通
风口的面积最大且它们之间的距离为
时,则两个正方形通风口关于 轴对
称,且正方形通风口的点, 在
轴上,点在抛物线上,且 .
设正方形的边长为 ,
则,代入 ,
得 ,
解得, (舍去),
故正方形通风口 的面积为
,
两个正方形通风口的面积为
.
,
第②种方案通风效果更好.
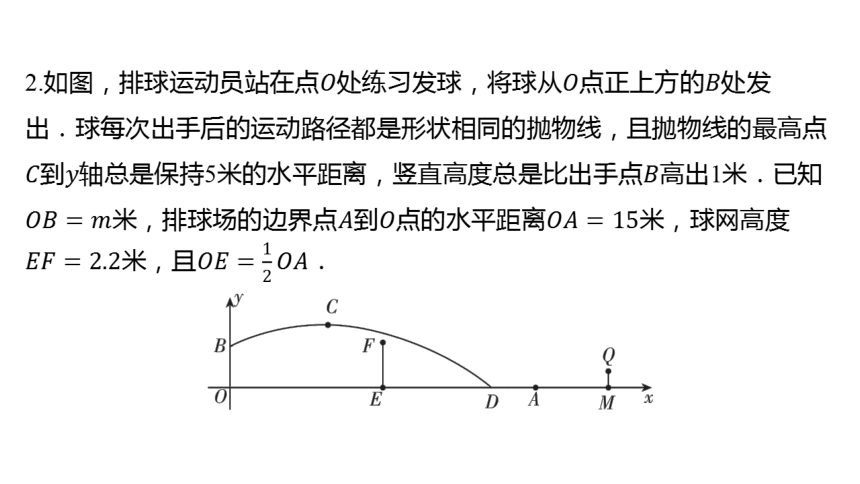
2.如图,排球运动员站在点处练习发球,将球从点正上方的 处发
出.球每次出手后的运动路径都是形状相同的抛物线,且抛物线的最高点
到轴总是保持5米的水平距离,竖直高度总是比出手点 高出1米.已知
米,排球场的边界点到点的水平距离 米,球网高度
米,且 .
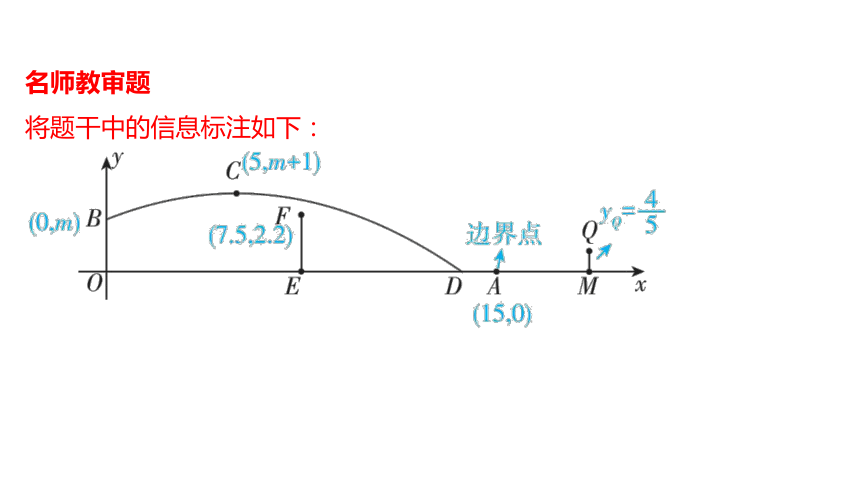
名师教审题
将题干中的信息标注如下:
①求排球运动路径所在抛物线的表达式.
【答案】由题意可得, ,
当时,, ,
可设抛物线的表达式为 ,
将代入,得 .
解得 ,
抛物线的表达式为 .
(1)当 时,
②排球能否越过球网?如果过网是否会出界?请说明理由.
【答案】球能越过球网,球不会出界,理由如下:
由①知,当时,抛物线的表达式为 .
米,, 米.
又米, .
当时, .
, 球能越过球网.
令,则 .
解得, ,
,0 .
, 球不会出界.
(2)若该运动员调整起跳高度,使球在点 处落地,此时形成的抛物线记
为,球落地后立即向右弹起,形成另一条与形状相同的抛物线 ,且
此时排球运行的最大高度为1米,球场外有一个标志牌, 轴于
点,米.若排球向右反弹后,沿 的路径在下落过程中恰好碰到
点,则点到点 的距离为__________米.
【解析】解法提示:设抛物线的表达式为 ,
将代入,得 ,
解得(舍去), ,
则抛物线的表达式为 ,
令 ,
解得 (不合题意的值已舍去).
故点到点的距离为 米.
3.新情境 模拟火箭的运行过程 16世纪中叶,我国发明了一种新式火箭“火龙
出水”(如图(1)),它是二级火箭的始祖.火箭第一级运行路径形如抛物线,
当火箭运行一定水平距离时,自动引发火箭第二级,火箭第二级沿直线运行.
图(1)
图(2)
某科技小组运用信息技术模拟火箭运行过程.如图(2),以发射点为原点,地
平线为轴,垂直于地面的直线为 轴,建立平面直角坐标系,分别得到抛物线
和直线.其中,当火箭运行的水平距离为 时,自
动引发火箭的第二级.
(1)若火箭第二级的引发点的高度为 ,
①直接写出, 的值.
【答案】,
【解析】解法提示: 火箭第二级的引发点的高度为3. ,
抛物线和直线均经过点 ,
, ,
, .
②火箭在运行过程中,有两个位置的高度比火箭运行的最高点低 ,求
这两个位置之间的距离.
【答案】由①知,直线,抛物线 ,
,
当时,取得最大值,为 .
.
令,解得(不符合题意,舍去),
(易错点:根据题意,抛物线上的点的横坐标满足 ).
令,解得 .
,
这两个位置之间的距离为 .
. .
(2)直接写出 满足什么条件时,火箭落地点与发射点的水平距离超过
.
【答案】 .
【解析】解法提示:把代入,得 ,
火箭第二级的引发点为 .
将代入,得 ,
.
令,解得 .
由题意,得,解得 ,
.
类型2 销售利润问题
4.某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单
价不低于进价时,日销售量(单位:盒)与销售单价 (单位:元)是一
次函数关系,下表是与 的几组对应值.
销售单价 元 … 12 14 16 18 20 …
日销售量 盒 … 56 52 48 44 40 …
(1)求与 的函数表达式.
【答案】设与的函数表达式为 .
把, 分别代入,
得解得
与的函数表达式为 .
(2)当糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少
【答案】设日销售利润为 元,
根据题意,得
,
当时, 有最大值,最大值为450.
答:当糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元.
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为 元的礼
品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求 的值.
【答案】设日销售利润为 元,
根据题意,得
,
当时, 有最大值,为
,
令 ,
化简得 ,
解得, ,
当时,, ,
的值为
5.综合与实践
问题情境
小莹妈妈的花卉超市以15元/盆的价格新购进了某种盆栽花卉,为了确定
售价,小莹帮妈妈调查了附近A,B,C,D, 五家花卉店近期该种盆栽
花卉的售价与日销售量情况,记录如下:
售价/(元/盆) 日销售量/盆
A 20 50
B 30 30
C 18 54
D 22 46
26 38
数据整理
(1)请将以上调查数据按照一定顺序重新整理,填写在下表中.
售价/(元/盆)
日销售量/盆
【答案】按照售价从低到高排列列出表格如下:
售价/(元/盆) 18 20 22 26 30
日销售量/盆 54 50 46 38 30
模型建立
(2)分析数据的变化规律,找出日销售量与售价间的关系.
【答案】售价每增加2元,日销售量少4盆,
或售价每增加1元,日销售量少2盆.
拓展应用
(3)根据以上信息,小莹妈妈在销售该种花卉时,
①要想每天获得400元的利润,应如何定价?
【答案】设定价为 元/盆,由题意,得
,
整理,得 ,
解得, ,
答:定价为每盆25元或每盆35元时,每天获得400元的利润.
②售价定为多少时,每天能够获得最大利润?
【答案】(第一步:设出未知数.)
设售价定为元/盆时,每天的利润为 元.
(第二步:找出关于 的关系式.)
由题意,得
,
,
(第三步:根据函数性质求出 的最大值.)
,
当时, 有最大值,最大值为450.
答:售价定为30元/盆时,每天能够获得最大利润.
6.请根据以下素材,完成探究任务.
制定加工方案 生 产 背 景 背景1 ◆ 某民族服装厂安排70名工人加工一批夏季服装,有“风”“雅”“正”三种样式.
◆ 因工艺需要,每位工人每天可加工且只能加工“风”服装2件,或
“雅”服装1件,或“正”服装1件.
◆ 要求全厂每天加工“雅”服装至少10件,“正”服装总件数和“风”服装相等.
生 产 背 景 背 景2 每天加工的服装都能销售出去,扣除各种成本,服装厂的获利情况为:
①“风”服装:24元/件;
②“正”服装:48元/件;
③“雅”服装:当每天加工10件时,每件获利100元;如果每天多加工1件,那么平均每件获利将减少2元.
信息整 理 现安排名工人加工“雅”服装, 名工人加工“风”服装,列表如下:
______________________________________________________________________________________________________
续表
名师教审题
题干①:某民族服装厂安排70名工人加工一批夏季服装,有“风”“雅”“正”
三种样式.
提取信息:“正”服装加工人数“风”服装加工人数 “雅”服装加工人数
.
题干②:因工艺需要,每位工人每天可加工且只能加工“风”服装2件,或
“雅”服装1件,或“正”服装1件.要求全厂每天加工“雅”服装至少10件,“正”
服装总件数和“风”服装相等.
提取信息:“正”服装加工人数“风”服装加工人数 .
题干③:“雅”服装:当每天加工10件时,每件获利100元;如果每天多加
工1件,那么平均每件获利将减少2元.
提取信息:“雅”服装平均每件获利为 元.
探究任务
任务1 探寻变量关系
求, 之间的数量关系.
【答案】 安排名工人加工“雅”服装, 名工人加工“风”服装,
加工“正”服装的有 人.
“正”服装总件数和“风”服装总件数相等,
,
整理,得 .
任务2 建立数学模型
设该工厂每天的总利润为元,求关于 的函数表达式.
______________________________________________________________________________________________________
【答案】根据题意,得“雅”服装每天获利为 ,
,
即 .
任务3 拟定加工方案
制定使每天总利润最大的加工方案.
【答案】由任务2,得 ,
由题意得, ,
,且 为整数.
,
当 时,获得最大利润.
又 ,不合题意,
.
当时,随 的增大而增大,
当时, ,不符合题意;
当时,随 的增大而减小,
当时, ,符合题意.
.
答:安排19名工人加工“雅”服装,17名工人加工“风”服装,34名工人加工“正”
服装,即可获得最大利润.
类型3 面积问题
7.如图,某校劳动实践基地用总长为 的栅栏,围成一块一边靠墙的矩形
实验田,墙长为 .栅栏在安装过程中不重叠、无损耗.设矩形实验田与墙
垂直的一边长为(单位:),与墙平行的一边长为(单位:),面积为
(单位: ).
名师教审题
题干:……某校劳动实践基地用总长为 的栅栏,围成一块一边靠墙的
矩形实验田,墙长为 .栅栏在安装过程中不重叠、无耗损.设矩形实验
田与墙垂直的一边长为单位:,与墙平行的一边长为单位: ,面
积为单位: .
提取信息:,, .
(1)直接写出与,与之间的函数解析式(不要求写 的取值范围).
【答案】, .
【解析】解法提示:由题意,得 ,
,
.
(2)矩形实验田的面积能达到吗 如果能,求 的值;如果不能,请说
明理由.
【答案】矩形实验田的面积能达到 .
令,则 ,
整理,得 ,
解得, .(5分)
墙长为 (易错点:易忽略墙长这一条件),
,
,
解得 ,
.
. .
(3)当的值是多少时,矩形实验田的面积 最大 最大面积是多少
【答案】 .
, ,
当时,取得最大值,此时 ,
即当时,最大,最大面积是 .
类型4 其他问题
8.从地面竖直向上发射的物体离地面的高度 满足关系式
,其中是物体运动的时间, 是物体被发射时的速
度.社团活动时,科学小组在实验楼前从地面竖直向上发射小球.
(1)小球被发射后___时离地面的高度最大(用含 的式子表示).
(2)若小球离地面的最大高度为 ,求小球被发射时的速度.
【答案】根据题意,得当时, ,
,
,即小球被发射时的速度为 .
(3)按(2)中的速度发射小球,小球离地面的高度有两次与实验楼的高度
相同.小明说:“这两次间隔的时间为.”已知实验楼高 ,请判断他的说法
是否正确,并说明理由.
【答案】小明的说法不正确.
理由如下:
由(2),得 .
当时, ,
解得, .
,
小明的说法不正确.
9.新情境 无人机滑行测试 某科研单位为保障某种型号的无人机能安全投
产,随机选择一架该种型号的无人机进行测试,测试该无人机在跑道上着
陆后滑行的情况,收集到的数据如下表.
滑行时间 0 1 2 3 4 …
滑行速度 30 28 26 24 22 …
滑行距离 0 29 56 81 104 …
已知该无人机在跑道上着陆后的滑行速度与滑行时间 之间满足一次函数
关系,滑行距离与滑行时间 之间满足二次函数关系.
(1)求关于的函数表达式和关于 的函数表达式.
【答案】设,将, 分别代入,
得解得
.
由题可知,当时, ,
可设 ,
将, 分别代入,
得解得
.
(2)求该无人机在跑道上着陆后滑行 时,无人机的滑行速度.
【答案】对于,当时, ,
无人机滑行 后停止.
对于 ,
当时, ,
解得, (不合题意,舍去).
当时, ,
无人机的滑行速度为 .
(3)求该无人机着陆后,以不大于 的速度滑行了多少米.
【答案】对于 ,
,随 的增大而减小.
令,解得 .
当时, ,
当时, .
,
该无人机着陆后,以不大于的速度滑行了 .
(4)若该无人机在跑道上开始滑行时,发现前方 处有另外一架无人
机以为整数,且 的速度匀速同向滑行,要保证被测试的无
人机无法追上前方的无人机,请直接写出 的最小值.
【答案】 的最小值为11.
【解析】解法提示:由题意知 .
设 ,
则 .
, ,
二次函数的图象的对称轴在 轴右侧,
,即 ,
,
又为整数, 的最小值为11.
感谢观看
题型六
二次函数实际应用题
2025年中考题型解析
类型1 抛物线形问题
1.如图,一厂房的顶部为抛物线的一部分,测得两端点,(点, 也
为抛物线上的对称点)之间的距离为,在上距点 处房顶的高
度 .
(1)建立适当的平面直角坐标系,并求出抛物线的表达式.
图(1)
【答案】以线段所在直线为轴,线段的中点
为坐标原点,建立平面直角坐标系如图(1)所示.
,,, .
, ,
.
设抛物线的表达式为 ,
将代入,得 ,
解得 ,
故抛物线的表达式为
.
(2)为了通风需要,房主想利用线段 与抛物线之间的部分建造通风口,
现有两种设计方案:
①建造一个正方形通风口,且面积最大;
②建造两个相同的面积最大的正方形通风口,且两通风口之间的距离为
.
通过计算说明哪种方案通风效果更好(通风口面积越大,通风效果越好.参
考数据: )
图(2)
【答案】第①种方案:如图(2),当正
方形通风口的面积最大时,点 ,
在轴上,点, 在抛物线上,且
,
设正方形的边长为 ,
则,代入 ,
得 ,
解得,
(舍去).
,
,
故正方形的面积约为 .
图(3)
第②种方案:如图(3),当两个相同通
风口的面积最大且它们之间的距离为
时,则两个正方形通风口关于 轴对
称,且正方形通风口的点, 在
轴上,点在抛物线上,且 .
设正方形的边长为 ,
则,代入 ,
得 ,
解得, (舍去),
故正方形通风口 的面积为
,
两个正方形通风口的面积为
.
,
第②种方案通风效果更好.
2.如图,排球运动员站在点处练习发球,将球从点正上方的 处发
出.球每次出手后的运动路径都是形状相同的抛物线,且抛物线的最高点
到轴总是保持5米的水平距离,竖直高度总是比出手点 高出1米.已知
米,排球场的边界点到点的水平距离 米,球网高度
米,且 .
名师教审题
将题干中的信息标注如下:
①求排球运动路径所在抛物线的表达式.
【答案】由题意可得, ,
当时,, ,
可设抛物线的表达式为 ,
将代入,得 .
解得 ,
抛物线的表达式为 .
(1)当 时,
②排球能否越过球网?如果过网是否会出界?请说明理由.
【答案】球能越过球网,球不会出界,理由如下:
由①知,当时,抛物线的表达式为 .
米,, 米.
又米, .
当时, .
, 球能越过球网.
令,则 .
解得, ,
,0 .
, 球不会出界.
(2)若该运动员调整起跳高度,使球在点 处落地,此时形成的抛物线记
为,球落地后立即向右弹起,形成另一条与形状相同的抛物线 ,且
此时排球运行的最大高度为1米,球场外有一个标志牌, 轴于
点,米.若排球向右反弹后,沿 的路径在下落过程中恰好碰到
点,则点到点 的距离为__________米.
【解析】解法提示:设抛物线的表达式为 ,
将代入,得 ,
解得(舍去), ,
则抛物线的表达式为 ,
令 ,
解得 (不合题意的值已舍去).
故点到点的距离为 米.
3.新情境 模拟火箭的运行过程 16世纪中叶,我国发明了一种新式火箭“火龙
出水”(如图(1)),它是二级火箭的始祖.火箭第一级运行路径形如抛物线,
当火箭运行一定水平距离时,自动引发火箭第二级,火箭第二级沿直线运行.
图(1)
图(2)
某科技小组运用信息技术模拟火箭运行过程.如图(2),以发射点为原点,地
平线为轴,垂直于地面的直线为 轴,建立平面直角坐标系,分别得到抛物线
和直线.其中,当火箭运行的水平距离为 时,自
动引发火箭的第二级.
(1)若火箭第二级的引发点的高度为 ,
①直接写出, 的值.
【答案】,
【解析】解法提示: 火箭第二级的引发点的高度为3. ,
抛物线和直线均经过点 ,
, ,
, .
②火箭在运行过程中,有两个位置的高度比火箭运行的最高点低 ,求
这两个位置之间的距离.
【答案】由①知,直线,抛物线 ,
,
当时,取得最大值,为 .
.
令,解得(不符合题意,舍去),
(易错点:根据题意,抛物线上的点的横坐标满足 ).
令,解得 .
,
这两个位置之间的距离为 .
. .
(2)直接写出 满足什么条件时,火箭落地点与发射点的水平距离超过
.
【答案】 .
【解析】解法提示:把代入,得 ,
火箭第二级的引发点为 .
将代入,得 ,
.
令,解得 .
由题意,得,解得 ,
.
类型2 销售利润问题
4.某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单
价不低于进价时,日销售量(单位:盒)与销售单价 (单位:元)是一
次函数关系,下表是与 的几组对应值.
销售单价 元 … 12 14 16 18 20 …
日销售量 盒 … 56 52 48 44 40 …
(1)求与 的函数表达式.
【答案】设与的函数表达式为 .
把, 分别代入,
得解得
与的函数表达式为 .
(2)当糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少
【答案】设日销售利润为 元,
根据题意,得
,
当时, 有最大值,最大值为450.
答:当糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元.
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为 元的礼
品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求 的值.
【答案】设日销售利润为 元,
根据题意,得
,
当时, 有最大值,为
,
令 ,
化简得 ,
解得, ,
当时,, ,
的值为
5.综合与实践
问题情境
小莹妈妈的花卉超市以15元/盆的价格新购进了某种盆栽花卉,为了确定
售价,小莹帮妈妈调查了附近A,B,C,D, 五家花卉店近期该种盆栽
花卉的售价与日销售量情况,记录如下:
售价/(元/盆) 日销售量/盆
A 20 50
B 30 30
C 18 54
D 22 46
26 38
数据整理
(1)请将以上调查数据按照一定顺序重新整理,填写在下表中.
售价/(元/盆)
日销售量/盆
【答案】按照售价从低到高排列列出表格如下:
售价/(元/盆) 18 20 22 26 30
日销售量/盆 54 50 46 38 30
模型建立
(2)分析数据的变化规律,找出日销售量与售价间的关系.
【答案】售价每增加2元,日销售量少4盆,
或售价每增加1元,日销售量少2盆.
拓展应用
(3)根据以上信息,小莹妈妈在销售该种花卉时,
①要想每天获得400元的利润,应如何定价?
【答案】设定价为 元/盆,由题意,得
,
整理,得 ,
解得, ,
答:定价为每盆25元或每盆35元时,每天获得400元的利润.
②售价定为多少时,每天能够获得最大利润?
【答案】(第一步:设出未知数.)
设售价定为元/盆时,每天的利润为 元.
(第二步:找出关于 的关系式.)
由题意,得
,
,
(第三步:根据函数性质求出 的最大值.)
,
当时, 有最大值,最大值为450.
答:售价定为30元/盆时,每天能够获得最大利润.
6.请根据以下素材,完成探究任务.
制定加工方案 生 产 背 景 背景1 ◆ 某民族服装厂安排70名工人加工一批夏季服装,有“风”“雅”“正”三种样式.
◆ 因工艺需要,每位工人每天可加工且只能加工“风”服装2件,或
“雅”服装1件,或“正”服装1件.
◆ 要求全厂每天加工“雅”服装至少10件,“正”服装总件数和“风”服装相等.
生 产 背 景 背 景2 每天加工的服装都能销售出去,扣除各种成本,服装厂的获利情况为:
①“风”服装:24元/件;
②“正”服装:48元/件;
③“雅”服装:当每天加工10件时,每件获利100元;如果每天多加工1件,那么平均每件获利将减少2元.
信息整 理 现安排名工人加工“雅”服装, 名工人加工“风”服装,列表如下:
______________________________________________________________________________________________________
续表
名师教审题
题干①:某民族服装厂安排70名工人加工一批夏季服装,有“风”“雅”“正”
三种样式.
提取信息:“正”服装加工人数“风”服装加工人数 “雅”服装加工人数
.
题干②:因工艺需要,每位工人每天可加工且只能加工“风”服装2件,或
“雅”服装1件,或“正”服装1件.要求全厂每天加工“雅”服装至少10件,“正”
服装总件数和“风”服装相等.
提取信息:“正”服装加工人数“风”服装加工人数 .
题干③:“雅”服装:当每天加工10件时,每件获利100元;如果每天多加
工1件,那么平均每件获利将减少2元.
提取信息:“雅”服装平均每件获利为 元.
探究任务
任务1 探寻变量关系
求, 之间的数量关系.
【答案】 安排名工人加工“雅”服装, 名工人加工“风”服装,
加工“正”服装的有 人.
“正”服装总件数和“风”服装总件数相等,
,
整理,得 .
任务2 建立数学模型
设该工厂每天的总利润为元,求关于 的函数表达式.
______________________________________________________________________________________________________
【答案】根据题意,得“雅”服装每天获利为 ,
,
即 .
任务3 拟定加工方案
制定使每天总利润最大的加工方案.
【答案】由任务2,得 ,
由题意得, ,
,且 为整数.
,
当 时,获得最大利润.
又 ,不合题意,
.
当时,随 的增大而增大,
当时, ,不符合题意;
当时,随 的增大而减小,
当时, ,符合题意.
.
答:安排19名工人加工“雅”服装,17名工人加工“风”服装,34名工人加工“正”
服装,即可获得最大利润.
类型3 面积问题
7.如图,某校劳动实践基地用总长为 的栅栏,围成一块一边靠墙的矩形
实验田,墙长为 .栅栏在安装过程中不重叠、无损耗.设矩形实验田与墙
垂直的一边长为(单位:),与墙平行的一边长为(单位:),面积为
(单位: ).
名师教审题
题干:……某校劳动实践基地用总长为 的栅栏,围成一块一边靠墙的
矩形实验田,墙长为 .栅栏在安装过程中不重叠、无耗损.设矩形实验
田与墙垂直的一边长为单位:,与墙平行的一边长为单位: ,面
积为单位: .
提取信息:,, .
(1)直接写出与,与之间的函数解析式(不要求写 的取值范围).
【答案】, .
【解析】解法提示:由题意,得 ,
,
.
(2)矩形实验田的面积能达到吗 如果能,求 的值;如果不能,请说
明理由.
【答案】矩形实验田的面积能达到 .
令,则 ,
整理,得 ,
解得, .(5分)
墙长为 (易错点:易忽略墙长这一条件),
,
,
解得 ,
.
. .
(3)当的值是多少时,矩形实验田的面积 最大 最大面积是多少
【答案】 .
, ,
当时,取得最大值,此时 ,
即当时,最大,最大面积是 .
类型4 其他问题
8.从地面竖直向上发射的物体离地面的高度 满足关系式
,其中是物体运动的时间, 是物体被发射时的速
度.社团活动时,科学小组在实验楼前从地面竖直向上发射小球.
(1)小球被发射后___时离地面的高度最大(用含 的式子表示).
(2)若小球离地面的最大高度为 ,求小球被发射时的速度.
【答案】根据题意,得当时, ,
,
,即小球被发射时的速度为 .
(3)按(2)中的速度发射小球,小球离地面的高度有两次与实验楼的高度
相同.小明说:“这两次间隔的时间为.”已知实验楼高 ,请判断他的说法
是否正确,并说明理由.
【答案】小明的说法不正确.
理由如下:
由(2),得 .
当时, ,
解得, .
,
小明的说法不正确.
9.新情境 无人机滑行测试 某科研单位为保障某种型号的无人机能安全投
产,随机选择一架该种型号的无人机进行测试,测试该无人机在跑道上着
陆后滑行的情况,收集到的数据如下表.
滑行时间 0 1 2 3 4 …
滑行速度 30 28 26 24 22 …
滑行距离 0 29 56 81 104 …
已知该无人机在跑道上着陆后的滑行速度与滑行时间 之间满足一次函数
关系,滑行距离与滑行时间 之间满足二次函数关系.
(1)求关于的函数表达式和关于 的函数表达式.
【答案】设,将, 分别代入,
得解得
.
由题可知,当时, ,
可设 ,
将, 分别代入,
得解得
.
(2)求该无人机在跑道上着陆后滑行 时,无人机的滑行速度.
【答案】对于,当时, ,
无人机滑行 后停止.
对于 ,
当时, ,
解得, (不合题意,舍去).
当时, ,
无人机的滑行速度为 .
(3)求该无人机着陆后,以不大于 的速度滑行了多少米.
【答案】对于 ,
,随 的增大而减小.
令,解得 .
当时, ,
当时, .
,
该无人机着陆后,以不大于的速度滑行了 .
(4)若该无人机在跑道上开始滑行时,发现前方 处有另外一架无人
机以为整数,且 的速度匀速同向滑行,要保证被测试的无
人机无法追上前方的无人机,请直接写出 的最小值.
【答案】 的最小值为11.
【解析】解法提示:由题意知 .
设 ,
则 .
, ,
二次函数的图象的对称轴在 轴右侧,
,即 ,
,
又为整数, 的最小值为11.
感谢观看
同课章节目录
