2025年中考数学压轴题型解析 题型七 二次函数图象与性质综合题 课件(共69张PPT)
文档属性
| 名称 | 2025年中考数学压轴题型解析 题型七 二次函数图象与性质综合题 课件(共69张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 16:00:18 | ||
图片预览




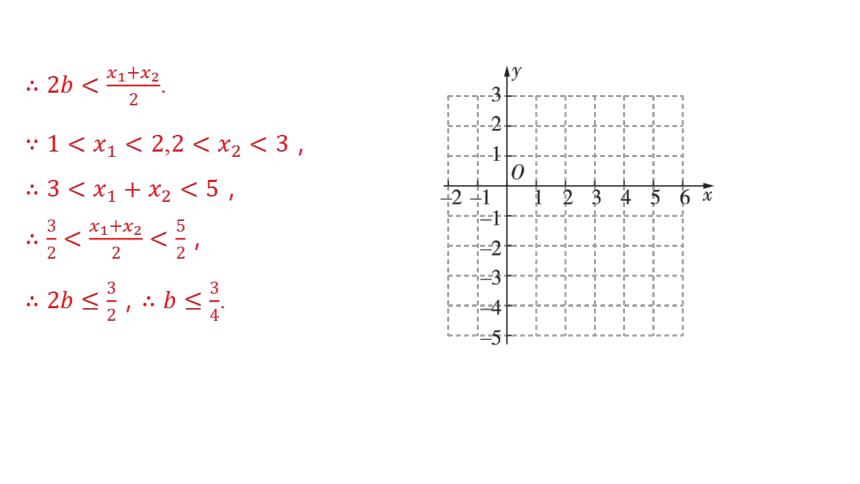




文档简介
(共69张PPT)
题型七
二次函数图象与性质综合题
2025年中考题型解析
类型1 含参问题
1.已知抛物线 .
(1)当 时:
①求该抛物线的顶点坐标,并直接在如图所示的平面直角坐标系中画出该
抛物线.
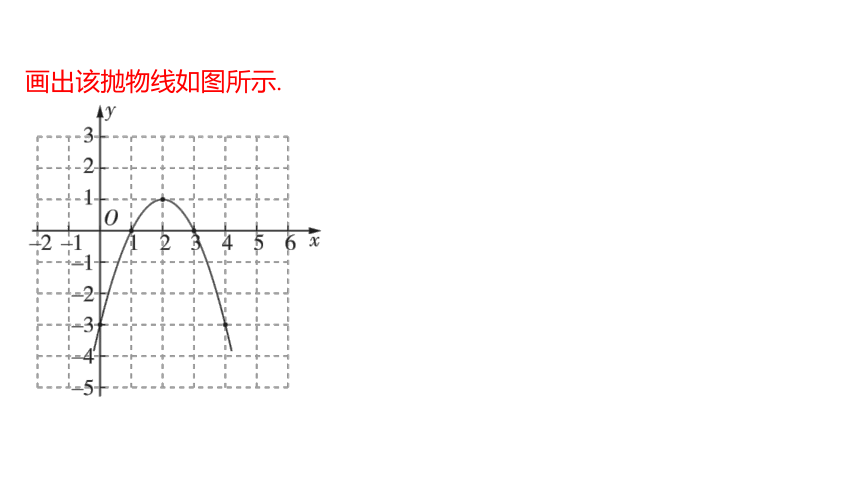
【答案】当时, ,
抛物线的顶点坐标为 .
画出该抛物线如图所示.
②若点是抛物线上一点,点的坐标为,直线 与抛物
线交于点(异于点),请直接用含的式子表示点 的横坐标,并求出
当时 的值.
【答案】点的横坐标为 .
,
(关键点),
,
,
或 .
. .
(2)点, 在抛物线上
,若对于, 的
任意取值,都有,求 的取值范
围.
【答案】 抛物线开口向下,
抛物线上离对称轴越近的点纵坐标越大.
又,抛物线的对称轴为直线 ,
点到直线的距离小于点 到直线
的距离.
由题意知点在点 左侧.
连接,则中点的横坐标为 .
由可知的中点在直线 右侧,
.
, ,
,
,
, .
2.新定义:我们把抛物线与抛物线
(其中)称为“伴随抛物线”.例如:抛物线 的“伴随
抛物线”为抛物线 .已知抛物线
的“伴随抛物线”为 .
(1)求出抛物线的解析式(用含 的式子表示)及顶点坐标.
【答案】根据“伴随抛物线”的定义可知,抛物线 的函数解析式为
.
,
抛物线的顶点坐标为 .
(2)过轴上一点,作轴的垂线分别交抛物线,于点, .当
时,求点 的坐标.
【答案】设点 ,
则, ,
.
,
,
或 .
对于,其根的判别式 ,
此方程无解,
对于 ,
解得, ,
点的坐标为或 .
(3)当时,抛物线的最大值与最小值的差为,求 的值.
【答案】对于抛物线 ,
当时, .
当时, ;
当时, .
,, ,故需要分两种情况讨论:
Ⅰ.当,即 时,
若,即 ,
则, ,
,
(不合题意的值已舍去);
若,即 ,
则, ,
,
(不合题意的值已舍去).
Ⅱ.当,即 时,
, ,
,
解得或 ,均不符合题意.
综上所述,的值为或 .
名师放大招
高分技法
利用二次函数的性质比较函数值大小的方法
1.代入比较法:若已知二次函数的解析式,可将各点的横坐标代入解析式,
求出各点的纵坐标,继而比较大小.
2.增减性比较法:利用二次函数图象的对称性,将已知点转化到对称轴的
同侧,再利用二次函数的增减性比较大小.
3.距离比较法:根据点到对称轴的距离比较大小,具体如下.
对于二次函数
①当 时,抛物线上的点到对称轴的距离越小,对应的函数值越小,
如图(1);
②当 时,抛物线上的点到对称轴的距离越小,对应的函数值越大,
如图(2).
图(1)
图(2)
3.如图,抛物线与轴交于, 两
点,与轴交于点,点为动点,且,过点作 轴的垂
线,交抛物线于点,交直线于点 .
(1)求,的值及抛物线 的顶点坐标.
【答案】将, 分别代入
,
得解得
,
抛物线的顶点坐标为, .
(2)若,求 的值.
【答案】由(1)可知 .
易知点的坐标为 ,
结合,可得直线 的解析式为
,
,
, ,
若,则 ,
解得, (舍去),
的值为1.
(3)平移抛物线得到抛物线,使抛物线 的
顶点为,将抛物线在 轴上方的部分记为图
象,若图象始终在抛物线的下方,求 的取
值范围.
【答案】由,可知抛物线 的解析
式为 .
当抛物线经过点(如抛物线)或经过点
(如抛物线 )时,如图所示.
把点的坐标 代入
,
得 ,
解得, (舍去).
把点的坐标代入 ,
得 ,
解得, (舍去).
综上可知,若图象始终在抛物线的下方,
的取值范围为 .
4.已知抛物线的顶点的横坐标比抛物线
的顶点的横坐标大4.
(1)求 的值.
【答案】 ,
抛物线的顶点坐标为 ,
抛物线的顶点的横坐标为 ,
, .
(2)若和都是抛物线上的点,且 ,求
的最小值.
【答案】由(1)可知抛物线 .
和都是抛物线 上的点,
, ,
.
,
,
.
,
的最小值是 .
(3)若点和都是抛物线上的点,且 ,对于某一
个确定的实数,若的最小值为1,求 的最大值.
【答案】 抛物线 ,
抛物线开口向上,对称轴为直线 .
点和都在抛物线上,且 ,
当取最小值1时,点和 都在对称轴的右侧.
此时, ,
①, ,
,解得 ,
,
此时点的坐标为,点的坐标为 .
当点是点关于直线的对称点时, 的值最大.
易知点关于直线的对称点的坐标为 ,
最大时, ,
的最大值为 .
5.在平面直角坐标系中,抛物线(是常数)与 轴交于点
,,与轴交于点,点 在抛物线上.
(1)求出抛物线的函数表达式和 的值.
【答案】将代入 ,
得, ,
抛物线的函数表达式为 .
对于,当时, ,
解得,, .
(2)点为轴下方的抛物线上一点,过点作轴的平行线,与直线
交于点,若线段的长为,求点 的横坐标.
【答案】设点 .
易知,由,可知直线的函数表达式为 .
对于,令 ,
则,故 .
设的长为 .
当时, ,
当时,取最大值 .
故此种情况舍去.
当时, .令
,则, (舍去).
故点的横坐标为 .
(3)点为直线上一动点,横坐标为,将点 向左平移1个单位长度,
得到点,若线段与抛物线恰好只有一个交点,求 的取值范围.
【答案】易知,则 .
当点落在抛物线上时, ,解得
, .
若,则线段 与抛物线无交点.
若,则当时,线段 与抛物线恰好只有一个交
点.
若,则当时,线段 与抛物线恰好只有一个交点.
综上,的取值范围为或 .
6.已知抛物线过点,,点是 轴正半轴上一
点,过点作轴的垂线,与抛物线交于点,点是 轴上一点,其纵坐标
为2,连接 .
(1)求抛物线的解析式.
【答案】将,代入 ,
得
解得
抛物线的解析式为 .
(2)试判断线段与 的数量关系,并说明理由.
【答案】 .
理由:根据题意画出符合题意的大致图象如图所示,
过点作 直线于点 ,
,, 轴,
, ,
,, ,
,
,
.
(3)点是轴上一点.设以,,, 为顶点的四边形的对角线的交
点为,是否存在点,使得?若存在,请求出 的值;若
不存在,请说明理由.
【答案】存在.
分两种情况讨论.
①当点在点上方时, ,
,
,
即 ,
,
解得, .
②当点在线段上时, ,
,
,
,
,
解得, (舍去).
综上可知,的值是2或6或 .
7.新考法 结合程序框图考查函数 小明利用一次函数和二次函数知识,设
计了一个计算程序,其程序框图如图(1)所示,输入的值为 时,输
出的值为1;输入的值为2时,输出的值为3;输入的值为3时,输出
的值为6.
图(1)
图(2)
(1)直接写出,, 的值.
【答案】,, .
(2)小明在平面直角坐标系中画出了关于 的函数图象,如图(2).
Ⅰ.当随的增大而增大时,求 的取值范围.
【答案】易知抛物线的对称轴为直线 .
结合图象可知,随的增大而增大时,或 .
Ⅱ.若关于的方程(为实数),在 时无解,
求 的取值范围.
【答案】方程可化为 .
由方程在时无解,可知当 时,抛物
线与直线 无交点.
当时,, 点 是抛物线的顶点.
当时, .
画出直线和 的位置,如图(1)所示,
图(1)
分析图象可知,当或时,抛物线与直线 在
的情况下无交点,即方程在 时无解.
Ⅲ.若在函数图象上有点,(与不重合)的横坐标为, 的横坐标
为.小明对,之间(含, 两点)的图象进行研究,当图象对应
函数的最大值与最小值均不随的变化而变化时,直接写出 的取值范围.
【答案】或 .
【解析】解法提示: ,
点,到直线 的距离相等.
如图(2),将代入,得, .
图(2)
将代入,得 .
作直线,, ,
分析可知,当点在直线和轴之间的图象上,或在直线 和直
线之间的图象上时(均含边界点),点, 之间的图象对应函数的
最大值与最小值分别为3和2,不随的变化而变化,故 的取值范围为
或 .
类型2 与几何图形有关
8.在平面直角坐标系中,点是坐标原点,直线 为常数,且
与轴交于点,抛物线的顶点为,且与 轴交
于点, .
(1)当点在直线上时,求 的值;
【答案】由抛物线经过坐标原点 ,
可知 ,
,
点的坐标是 .
当点在直线上时, .
又 ,
.
(2)当点在直线下方时,求点到直线 距离的最大值;
【答案】设点到直线的距离为 .
当点在直线下方时, ,
配方,得 .
当时, ,
点与直线 距离的最大值是1.
(3)当时,求 的面积.
【答案】将代入,得 ,
解得, ,
,
,
.
,
点在直线 上方.
如图,过点作轴于点,则 ,
.
,, ,
,解得(舍去), ,
, ,
, ,
.
9.已知抛物线与轴交于点,,与轴交于点 ,
抛物线的对称轴为直线 .
(1)求, 的值.
【答案】 抛物线与轴交于点, ,且对称轴为
直线 ,
点的坐标为 .
将,分别代入 ,
得
解得
(2)点是直线下方的抛物线上一动点,过点分别作 轴交直线
于点,轴交直线于点 .
(ⅰ)求线段 的最大值;
【答案】对于,当时, ,
,
.
又 , .
又轴, 轴,
,
.
设直线的表达式为 ,
将,分别代入,得
解得
直线的表达式为 .
设, ,
则 .
,
当时, 取最大值2,
的最大值为 .
(ⅱ)连接,当线段把的面积分成的两部分时,求点 的
横坐标.
【答案】如图,延长交轴于点 .
, ,
当线段把的面积分成的两部分时, 或
.
设, ,
则, .
.当时, ,
整理,得,解得(舍去), .
.当时, ,
整理,得,解得(舍去), .
综上可知,当线段把的面积分成的两部分时,点 的横坐标
为或 .
10.如图,在平面直角坐标系中,抛物线 的顶点为
.直线过点,且平行于轴,与抛物线交于, 两
点(在的右侧).将抛物线沿直线翻折得到抛物线,抛物线交
轴于点,顶点为 .
备用图
(1)当时,求点 的坐标;
【答案】 ,
抛物线的顶点的坐标为 .
,点和点关于直线 对称,
.
(2)连接,,,若为直角三角形,求此时抛物线 所对
应的函数表达式;
【答案】由题意,得抛物线的顶点与抛物线的顶点 关于直线
对称(关键点),
, 抛物线
.
当时,可得 .
图(1)
①当 时,如图(1),过点作 轴,垂足
为 .
, .
,, .
, .
直线轴, ,
, .
, ,
.
又 点在抛物线 上,
,
解得或 .
当时,可得,,此时, 重合,舍去.
当 时,符合题意.
将代入抛物线 ,得
.
图(2)
②当 时,如图(2),过点作 轴于点
,过点作,交的延长线于点 .
同理可得 .
, .
, ,
.
又 点在抛物线 上,
,解得或 .
,.此时, 符合题意.
将代入抛物线 ,得
.
③易知,当 时,此情况不存在.
综上,抛物线所对应的函数表达式为 或
.
(3)在(2)的条件下,若的面积为3,,两点分别在边 ,
上运动,且,以为一边作正方形,连接,写出
长度的最小值,并简要说明理由.
【答案】长度的最小值为.理由:由(2)知,当 时,
,此时 的面积为1,不合题意,舍去.
图(3)
如图(3),当 时,,此时 的面积为
3,符合题意.
由题意可求得 .
取的中点,连接 .
在中可求得 .
在中可求得 .
易知当,,三点共线时,取最小值,最小值为 .
感谢观看
题型七
二次函数图象与性质综合题
2025年中考题型解析
类型1 含参问题
1.已知抛物线 .
(1)当 时:
①求该抛物线的顶点坐标,并直接在如图所示的平面直角坐标系中画出该
抛物线.
【答案】当时, ,
抛物线的顶点坐标为 .
画出该抛物线如图所示.
②若点是抛物线上一点,点的坐标为,直线 与抛物
线交于点(异于点),请直接用含的式子表示点 的横坐标,并求出
当时 的值.
【答案】点的横坐标为 .
,
(关键点),
,
,
或 .
. .
(2)点, 在抛物线上
,若对于, 的
任意取值,都有,求 的取值范
围.
【答案】 抛物线开口向下,
抛物线上离对称轴越近的点纵坐标越大.
又,抛物线的对称轴为直线 ,
点到直线的距离小于点 到直线
的距离.
由题意知点在点 左侧.
连接,则中点的横坐标为 .
由可知的中点在直线 右侧,
.
, ,
,
,
, .
2.新定义:我们把抛物线与抛物线
(其中)称为“伴随抛物线”.例如:抛物线 的“伴随
抛物线”为抛物线 .已知抛物线
的“伴随抛物线”为 .
(1)求出抛物线的解析式(用含 的式子表示)及顶点坐标.
【答案】根据“伴随抛物线”的定义可知,抛物线 的函数解析式为
.
,
抛物线的顶点坐标为 .
(2)过轴上一点,作轴的垂线分别交抛物线,于点, .当
时,求点 的坐标.
【答案】设点 ,
则, ,
.
,
,
或 .
对于,其根的判别式 ,
此方程无解,
对于 ,
解得, ,
点的坐标为或 .
(3)当时,抛物线的最大值与最小值的差为,求 的值.
【答案】对于抛物线 ,
当时, .
当时, ;
当时, .
,, ,故需要分两种情况讨论:
Ⅰ.当,即 时,
若,即 ,
则, ,
,
(不合题意的值已舍去);
若,即 ,
则, ,
,
(不合题意的值已舍去).
Ⅱ.当,即 时,
, ,
,
解得或 ,均不符合题意.
综上所述,的值为或 .
名师放大招
高分技法
利用二次函数的性质比较函数值大小的方法
1.代入比较法:若已知二次函数的解析式,可将各点的横坐标代入解析式,
求出各点的纵坐标,继而比较大小.
2.增减性比较法:利用二次函数图象的对称性,将已知点转化到对称轴的
同侧,再利用二次函数的增减性比较大小.
3.距离比较法:根据点到对称轴的距离比较大小,具体如下.
对于二次函数
①当 时,抛物线上的点到对称轴的距离越小,对应的函数值越小,
如图(1);
②当 时,抛物线上的点到对称轴的距离越小,对应的函数值越大,
如图(2).
图(1)
图(2)
3.如图,抛物线与轴交于, 两
点,与轴交于点,点为动点,且,过点作 轴的垂
线,交抛物线于点,交直线于点 .
(1)求,的值及抛物线 的顶点坐标.
【答案】将, 分别代入
,
得解得
,
抛物线的顶点坐标为, .
(2)若,求 的值.
【答案】由(1)可知 .
易知点的坐标为 ,
结合,可得直线 的解析式为
,
,
, ,
若,则 ,
解得, (舍去),
的值为1.
(3)平移抛物线得到抛物线,使抛物线 的
顶点为,将抛物线在 轴上方的部分记为图
象,若图象始终在抛物线的下方,求 的取
值范围.
【答案】由,可知抛物线 的解析
式为 .
当抛物线经过点(如抛物线)或经过点
(如抛物线 )时,如图所示.
把点的坐标 代入
,
得 ,
解得, (舍去).
把点的坐标代入 ,
得 ,
解得, (舍去).
综上可知,若图象始终在抛物线的下方,
的取值范围为 .
4.已知抛物线的顶点的横坐标比抛物线
的顶点的横坐标大4.
(1)求 的值.
【答案】 ,
抛物线的顶点坐标为 ,
抛物线的顶点的横坐标为 ,
, .
(2)若和都是抛物线上的点,且 ,求
的最小值.
【答案】由(1)可知抛物线 .
和都是抛物线 上的点,
, ,
.
,
,
.
,
的最小值是 .
(3)若点和都是抛物线上的点,且 ,对于某一
个确定的实数,若的最小值为1,求 的最大值.
【答案】 抛物线 ,
抛物线开口向上,对称轴为直线 .
点和都在抛物线上,且 ,
当取最小值1时,点和 都在对称轴的右侧.
此时, ,
①, ,
,解得 ,
,
此时点的坐标为,点的坐标为 .
当点是点关于直线的对称点时, 的值最大.
易知点关于直线的对称点的坐标为 ,
最大时, ,
的最大值为 .
5.在平面直角坐标系中,抛物线(是常数)与 轴交于点
,,与轴交于点,点 在抛物线上.
(1)求出抛物线的函数表达式和 的值.
【答案】将代入 ,
得, ,
抛物线的函数表达式为 .
对于,当时, ,
解得,, .
(2)点为轴下方的抛物线上一点,过点作轴的平行线,与直线
交于点,若线段的长为,求点 的横坐标.
【答案】设点 .
易知,由,可知直线的函数表达式为 .
对于,令 ,
则,故 .
设的长为 .
当时, ,
当时,取最大值 .
故此种情况舍去.
当时, .令
,则, (舍去).
故点的横坐标为 .
(3)点为直线上一动点,横坐标为,将点 向左平移1个单位长度,
得到点,若线段与抛物线恰好只有一个交点,求 的取值范围.
【答案】易知,则 .
当点落在抛物线上时, ,解得
, .
若,则线段 与抛物线无交点.
若,则当时,线段 与抛物线恰好只有一个交
点.
若,则当时,线段 与抛物线恰好只有一个交点.
综上,的取值范围为或 .
6.已知抛物线过点,,点是 轴正半轴上一
点,过点作轴的垂线,与抛物线交于点,点是 轴上一点,其纵坐标
为2,连接 .
(1)求抛物线的解析式.
【答案】将,代入 ,
得
解得
抛物线的解析式为 .
(2)试判断线段与 的数量关系,并说明理由.
【答案】 .
理由:根据题意画出符合题意的大致图象如图所示,
过点作 直线于点 ,
,, 轴,
, ,
,, ,
,
,
.
(3)点是轴上一点.设以,,, 为顶点的四边形的对角线的交
点为,是否存在点,使得?若存在,请求出 的值;若
不存在,请说明理由.
【答案】存在.
分两种情况讨论.
①当点在点上方时, ,
,
,
即 ,
,
解得, .
②当点在线段上时, ,
,
,
,
,
解得, (舍去).
综上可知,的值是2或6或 .
7.新考法 结合程序框图考查函数 小明利用一次函数和二次函数知识,设
计了一个计算程序,其程序框图如图(1)所示,输入的值为 时,输
出的值为1;输入的值为2时,输出的值为3;输入的值为3时,输出
的值为6.
图(1)
图(2)
(1)直接写出,, 的值.
【答案】,, .
(2)小明在平面直角坐标系中画出了关于 的函数图象,如图(2).
Ⅰ.当随的增大而增大时,求 的取值范围.
【答案】易知抛物线的对称轴为直线 .
结合图象可知,随的增大而增大时,或 .
Ⅱ.若关于的方程(为实数),在 时无解,
求 的取值范围.
【答案】方程可化为 .
由方程在时无解,可知当 时,抛物
线与直线 无交点.
当时,, 点 是抛物线的顶点.
当时, .
画出直线和 的位置,如图(1)所示,
图(1)
分析图象可知,当或时,抛物线与直线 在
的情况下无交点,即方程在 时无解.
Ⅲ.若在函数图象上有点,(与不重合)的横坐标为, 的横坐标
为.小明对,之间(含, 两点)的图象进行研究,当图象对应
函数的最大值与最小值均不随的变化而变化时,直接写出 的取值范围.
【答案】或 .
【解析】解法提示: ,
点,到直线 的距离相等.
如图(2),将代入,得, .
图(2)
将代入,得 .
作直线,, ,
分析可知,当点在直线和轴之间的图象上,或在直线 和直
线之间的图象上时(均含边界点),点, 之间的图象对应函数的
最大值与最小值分别为3和2,不随的变化而变化,故 的取值范围为
或 .
类型2 与几何图形有关
8.在平面直角坐标系中,点是坐标原点,直线 为常数,且
与轴交于点,抛物线的顶点为,且与 轴交
于点, .
(1)当点在直线上时,求 的值;
【答案】由抛物线经过坐标原点 ,
可知 ,
,
点的坐标是 .
当点在直线上时, .
又 ,
.
(2)当点在直线下方时,求点到直线 距离的最大值;
【答案】设点到直线的距离为 .
当点在直线下方时, ,
配方,得 .
当时, ,
点与直线 距离的最大值是1.
(3)当时,求 的面积.
【答案】将代入,得 ,
解得, ,
,
,
.
,
点在直线 上方.
如图,过点作轴于点,则 ,
.
,, ,
,解得(舍去), ,
, ,
, ,
.
9.已知抛物线与轴交于点,,与轴交于点 ,
抛物线的对称轴为直线 .
(1)求, 的值.
【答案】 抛物线与轴交于点, ,且对称轴为
直线 ,
点的坐标为 .
将,分别代入 ,
得
解得
(2)点是直线下方的抛物线上一动点,过点分别作 轴交直线
于点,轴交直线于点 .
(ⅰ)求线段 的最大值;
【答案】对于,当时, ,
,
.
又 , .
又轴, 轴,
,
.
设直线的表达式为 ,
将,分别代入,得
解得
直线的表达式为 .
设, ,
则 .
,
当时, 取最大值2,
的最大值为 .
(ⅱ)连接,当线段把的面积分成的两部分时,求点 的
横坐标.
【答案】如图,延长交轴于点 .
, ,
当线段把的面积分成的两部分时, 或
.
设, ,
则, .
.当时, ,
整理,得,解得(舍去), .
.当时, ,
整理,得,解得(舍去), .
综上可知,当线段把的面积分成的两部分时,点 的横坐标
为或 .
10.如图,在平面直角坐标系中,抛物线 的顶点为
.直线过点,且平行于轴,与抛物线交于, 两
点(在的右侧).将抛物线沿直线翻折得到抛物线,抛物线交
轴于点,顶点为 .
备用图
(1)当时,求点 的坐标;
【答案】 ,
抛物线的顶点的坐标为 .
,点和点关于直线 对称,
.
(2)连接,,,若为直角三角形,求此时抛物线 所对
应的函数表达式;
【答案】由题意,得抛物线的顶点与抛物线的顶点 关于直线
对称(关键点),
, 抛物线
.
当时,可得 .
图(1)
①当 时,如图(1),过点作 轴,垂足
为 .
, .
,, .
, .
直线轴, ,
, .
, ,
.
又 点在抛物线 上,
,
解得或 .
当时,可得,,此时, 重合,舍去.
当 时,符合题意.
将代入抛物线 ,得
.
图(2)
②当 时,如图(2),过点作 轴于点
,过点作,交的延长线于点 .
同理可得 .
, .
, ,
.
又 点在抛物线 上,
,解得或 .
,.此时, 符合题意.
将代入抛物线 ,得
.
③易知,当 时,此情况不存在.
综上,抛物线所对应的函数表达式为 或
.
(3)在(2)的条件下,若的面积为3,,两点分别在边 ,
上运动,且,以为一边作正方形,连接,写出
长度的最小值,并简要说明理由.
【答案】长度的最小值为.理由:由(2)知,当 时,
,此时 的面积为1,不合题意,舍去.
图(3)
如图(3),当 时,,此时 的面积为
3,符合题意.
由题意可求得 .
取的中点,连接 .
在中可求得 .
在中可求得 .
易知当,,三点共线时,取最小值,最小值为 .
感谢观看
同课章节目录
