2.5 一元一次不等式与一次函数 分层训练(含答案)初中数学北师大版八年级下册
文档属性
| 名称 | 2.5 一元一次不等式与一次函数 分层训练(含答案)初中数学北师大版八年级下册 | 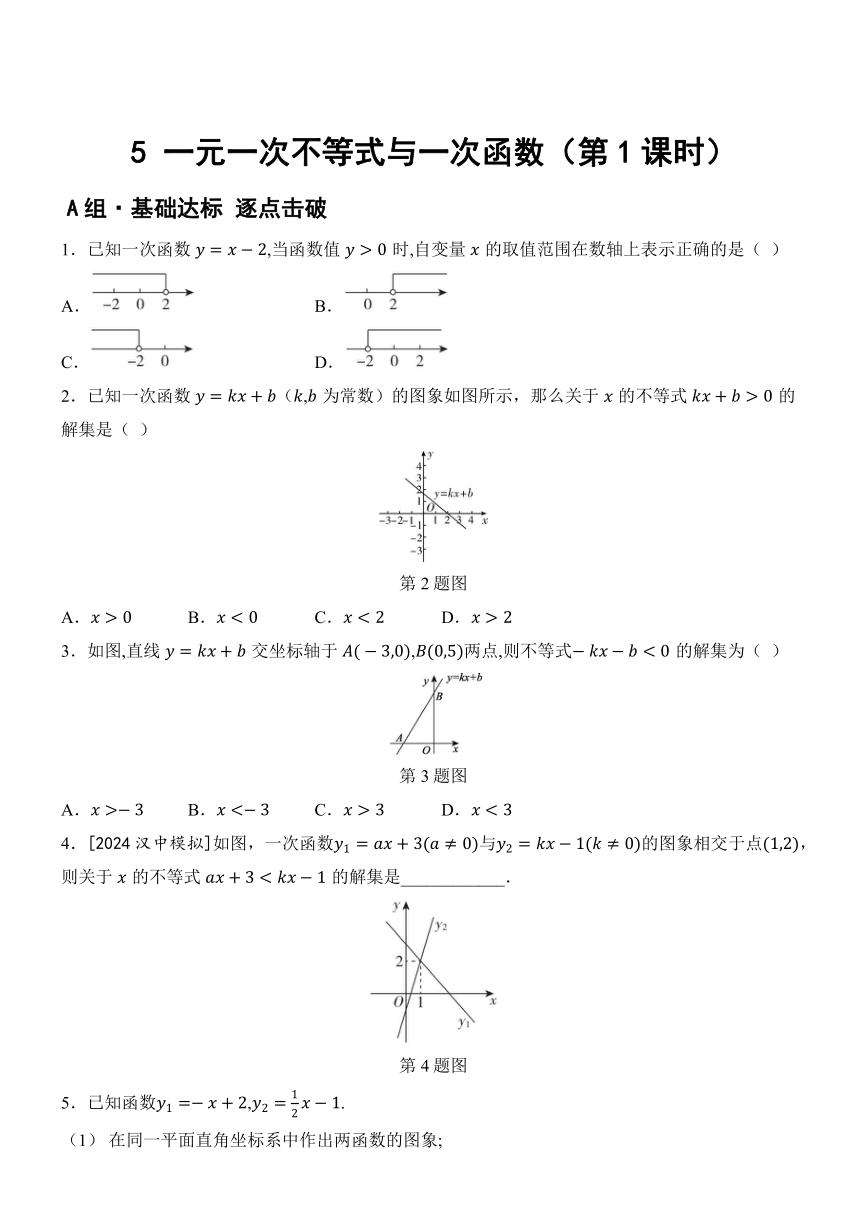 | |
| 格式 | docx | ||
| 文件大小 | 133.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 22:15:20 | ||
图片预览



文档简介
5 一元一次不等式与一次函数(第1课时)
A组·基础达标 逐点击破
1.已知一次函数,当函数值时,自变量的取值范围在数轴上表示正确的是( )
A. B.
C. D.
2.已知一次函数(,为常数)的图象如图所示,那么关于的不等式的解集是( )
第2题图
A. B. C. D.
3.如图,直线交坐标轴于,两点,则不等式的解集为( )
第3题图
A. B. C. D.
4.[2024汉中模拟]如图,一次函数与的图象相交于点,则关于的不等式的解集是____________.
第4题图
5.已知函数,.
(1) 在同一平面直角坐标系中作出两函数的图象;
(2) 观察图象,回答下列问题:
① 当取何值时,?
② 当取何值时,?
③ 当取何值时,?
B组·能力提升 强化突破
6.一次函数与的图象如图所示,有下列结论:;,;③当时,;④不等式的解集是.其中正确的结论个数是( )
A.0 B.1 C.2 D.3
7.如图,直线与轴交于点,直线分别与轴交于点,与轴交于点,两条直线相交于点,连接.
(1) 求两直线交点的坐标;
(2) 求的面积;
(3) 根据图象直接写出时自变量的取值范围.
C组·核心素养拓展 素养渗透
8.[2024北京]【模型观念】在平面直角坐标系中,函数与的图象交于点.
(1) 求,的值;
(2) 当时,对于的每一个值,函数的值既大于函数的值,也大于函数的值,直接写出的取值范围.
5 一元一次不等式与一次函数(第2课时)
A组·基础达标 逐点击破
1.若甲、乙两弹簧的长度与所挂物体质量之间的函数表达式分别为和,如图所示,所挂物体质量均为时,甲弹簧长为,乙弹簧长为,则与的大小关系为( )
A. B. C. D.不能确定
2.近年来,市民交通安全意识逐步增强,头盔需求量增大.某商店购进甲、乙两种头盔,已知购买甲种头盔20只,乙种头盔30只,共花费2 920元,甲种头盔的单价比乙种头盔的单价高11元.
(1) 甲、乙两种头盔的单价各是多少元?
(2) 该商店决定再次购进甲、乙两种头盔共40只,正好赶上厂家进行促销活动,促销方式如下:甲种头盔按单价的八折出售,乙种头盔每只降价6元出售.如果此次购买甲种头盔的数量不低于乙种头盔数量的一半,那么应购买多少只甲种头盔,才能使此次购买头盔的总费用最少?最少总费用是多少元?
3.为促进生产,公司提供了两种付给员工月报酬的方案,如图所示,员工可以任选一种方案与公司签订合同.根据图中所给信息,解答下列问题:
(1) 直接写出员工生产多少件产品时,两种方案付给的报酬一样多;
(2) 求方案二中关于的函数表达式;
(3) 如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案?
B组·能力提升 强化突破
4.[2024深圳模拟]某公司决定为优秀员工购买A,B两种奖品,已知购买3个A种奖品比购买2个B种奖品多花140元,购买4个A种奖品与购买5个B种奖品所需钱数相同.
(1) A,B两种奖品每个的价格分别为____________元、__________元;
(2) 商家推出了促销活动,A种奖品打九折.若该公司打算购买A,B两种奖品共30个,且B种奖品的个数不多于A种奖品个数的一半,则该公司最少花费多少钱?
C组·核心素养拓展 素养渗透
5.[2024南昌模拟]剪纸是一种镂空艺术,在视觉上给人以透空的感觉和艺术享受,剪纸内容多,寓意广,生活气息浓厚.某商家在春节前夕购进甲、乙两种剪纸装饰套装共60套进行销售,已知购进一套甲种剪纸比购进一套乙种剪纸多10元,购进2套甲种剪纸和3套乙种剪纸共需220元.
(1) 甲、乙两种剪纸购进时的单价分别为__________元、__________元;
(2) 设购进甲种剪纸装饰套,购买甲、乙两种剪纸装饰共花费元,求与之间的函数关系式;
(3) 若甲种剪纸的售价为65元/套,乙种剪纸的售价为50元/套,该商家计划购进这批剪纸装饰所花的总费用不超过2 800元,要使这批剪纸装饰全部售完时商家能获得最大利润,请你帮助商家设计购进方案,并求出最大利润.
5 一元一次不等式与一次函数(第1课时)
A组·基础达标 逐点击破
1.B 2.C 3.A
4.
5.(1) 解:作图如答图.
第5题答图
(2) ① 当时,.
② 当时,.
③ 当时,.
B组·能力提升 强化突破
6.D
7.(1) 解:将点代入,得;
将点代入,得.
联立解得故点的坐标为.
(2) 由可知,点的坐标为,.
.
(3) 由图可知,当在点的左侧时,,即时,.
C组·核心素养拓展 素养渗透
8.(1) 解: 直线过点,
,解得.
将点代入,得,
解得.
(2) 如答图,
第8题答图
当时,对于的每一个值,函数的值既大于函数的值,也大于函数的值,
.
的取值范围是.
5 一元一次不等式与一次函数(第2课时)
A组·基础达标 逐点击破
1.A
2.(1) 解:甲种头盔的单价是65元,乙种头盔的单价是54元.
(2) 设再次购进甲种头盔只,总费用为元,
根据题意,得,解得.
,
,随的增大而增大,
当时,取得最小值,(元).
答:购买14只甲种头盔时,总费用最少,最少总费用为1 976元.
3.(1) 解:员工生产30件产品时,两种方案付给的报酬一样多.
(2) 方案二中关于的函数表达式为.
(3) 由两方案的函数图象交于点可知:
若每月生产产品不足30件,则选择方案二;
若每月生产产品刚好30件,两种方案报酬相同,可以任选一种;
若每月生产产品超过30件,则选择方案一.
B组·能力提升 强化突破
4.(1) ;
(2) 解:设购买A种奖品个,则购买B种奖品个,
根据题意,得,解得.
设购买奖品的总费用为元,
根据题意,得,
,随的增大而增大.
当时,取得最小值,.
答:该公司最少花费2 600元.
C组·核心素养拓展 素养渗透
5.(1) ;
(2) 解:与之间的函数关系式为.
(3) 设甲、乙两种剪纸装饰获得的利润为元,
根据题意,得,即,
,随的增大而增大,
该商家计划购进这批剪纸装饰所花的总费用不超过2 800元,
,即,解得.
为非负整数, 当时,取得最大值,(元),
此时.
答:商家购进甲种剪纸装饰40套,乙种剪纸装饰20套时,所获利润最大,最大利润为800元.
A组·基础达标 逐点击破
1.已知一次函数,当函数值时,自变量的取值范围在数轴上表示正确的是( )
A. B.
C. D.
2.已知一次函数(,为常数)的图象如图所示,那么关于的不等式的解集是( )
第2题图
A. B. C. D.
3.如图,直线交坐标轴于,两点,则不等式的解集为( )
第3题图
A. B. C. D.
4.[2024汉中模拟]如图,一次函数与的图象相交于点,则关于的不等式的解集是____________.
第4题图
5.已知函数,.
(1) 在同一平面直角坐标系中作出两函数的图象;
(2) 观察图象,回答下列问题:
① 当取何值时,?
② 当取何值时,?
③ 当取何值时,?
B组·能力提升 强化突破
6.一次函数与的图象如图所示,有下列结论:;,;③当时,;④不等式的解集是.其中正确的结论个数是( )
A.0 B.1 C.2 D.3
7.如图,直线与轴交于点,直线分别与轴交于点,与轴交于点,两条直线相交于点,连接.
(1) 求两直线交点的坐标;
(2) 求的面积;
(3) 根据图象直接写出时自变量的取值范围.
C组·核心素养拓展 素养渗透
8.[2024北京]【模型观念】在平面直角坐标系中,函数与的图象交于点.
(1) 求,的值;
(2) 当时,对于的每一个值,函数的值既大于函数的值,也大于函数的值,直接写出的取值范围.
5 一元一次不等式与一次函数(第2课时)
A组·基础达标 逐点击破
1.若甲、乙两弹簧的长度与所挂物体质量之间的函数表达式分别为和,如图所示,所挂物体质量均为时,甲弹簧长为,乙弹簧长为,则与的大小关系为( )
A. B. C. D.不能确定
2.近年来,市民交通安全意识逐步增强,头盔需求量增大.某商店购进甲、乙两种头盔,已知购买甲种头盔20只,乙种头盔30只,共花费2 920元,甲种头盔的单价比乙种头盔的单价高11元.
(1) 甲、乙两种头盔的单价各是多少元?
(2) 该商店决定再次购进甲、乙两种头盔共40只,正好赶上厂家进行促销活动,促销方式如下:甲种头盔按单价的八折出售,乙种头盔每只降价6元出售.如果此次购买甲种头盔的数量不低于乙种头盔数量的一半,那么应购买多少只甲种头盔,才能使此次购买头盔的总费用最少?最少总费用是多少元?
3.为促进生产,公司提供了两种付给员工月报酬的方案,如图所示,员工可以任选一种方案与公司签订合同.根据图中所给信息,解答下列问题:
(1) 直接写出员工生产多少件产品时,两种方案付给的报酬一样多;
(2) 求方案二中关于的函数表达式;
(3) 如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案?
B组·能力提升 强化突破
4.[2024深圳模拟]某公司决定为优秀员工购买A,B两种奖品,已知购买3个A种奖品比购买2个B种奖品多花140元,购买4个A种奖品与购买5个B种奖品所需钱数相同.
(1) A,B两种奖品每个的价格分别为____________元、__________元;
(2) 商家推出了促销活动,A种奖品打九折.若该公司打算购买A,B两种奖品共30个,且B种奖品的个数不多于A种奖品个数的一半,则该公司最少花费多少钱?
C组·核心素养拓展 素养渗透
5.[2024南昌模拟]剪纸是一种镂空艺术,在视觉上给人以透空的感觉和艺术享受,剪纸内容多,寓意广,生活气息浓厚.某商家在春节前夕购进甲、乙两种剪纸装饰套装共60套进行销售,已知购进一套甲种剪纸比购进一套乙种剪纸多10元,购进2套甲种剪纸和3套乙种剪纸共需220元.
(1) 甲、乙两种剪纸购进时的单价分别为__________元、__________元;
(2) 设购进甲种剪纸装饰套,购买甲、乙两种剪纸装饰共花费元,求与之间的函数关系式;
(3) 若甲种剪纸的售价为65元/套,乙种剪纸的售价为50元/套,该商家计划购进这批剪纸装饰所花的总费用不超过2 800元,要使这批剪纸装饰全部售完时商家能获得最大利润,请你帮助商家设计购进方案,并求出最大利润.
5 一元一次不等式与一次函数(第1课时)
A组·基础达标 逐点击破
1.B 2.C 3.A
4.
5.(1) 解:作图如答图.
第5题答图
(2) ① 当时,.
② 当时,.
③ 当时,.
B组·能力提升 强化突破
6.D
7.(1) 解:将点代入,得;
将点代入,得.
联立解得故点的坐标为.
(2) 由可知,点的坐标为,.
.
(3) 由图可知,当在点的左侧时,,即时,.
C组·核心素养拓展 素养渗透
8.(1) 解: 直线过点,
,解得.
将点代入,得,
解得.
(2) 如答图,
第8题答图
当时,对于的每一个值,函数的值既大于函数的值,也大于函数的值,
.
的取值范围是.
5 一元一次不等式与一次函数(第2课时)
A组·基础达标 逐点击破
1.A
2.(1) 解:甲种头盔的单价是65元,乙种头盔的单价是54元.
(2) 设再次购进甲种头盔只,总费用为元,
根据题意,得,解得.
,
,随的增大而增大,
当时,取得最小值,(元).
答:购买14只甲种头盔时,总费用最少,最少总费用为1 976元.
3.(1) 解:员工生产30件产品时,两种方案付给的报酬一样多.
(2) 方案二中关于的函数表达式为.
(3) 由两方案的函数图象交于点可知:
若每月生产产品不足30件,则选择方案二;
若每月生产产品刚好30件,两种方案报酬相同,可以任选一种;
若每月生产产品超过30件,则选择方案一.
B组·能力提升 强化突破
4.(1) ;
(2) 解:设购买A种奖品个,则购买B种奖品个,
根据题意,得,解得.
设购买奖品的总费用为元,
根据题意,得,
,随的增大而增大.
当时,取得最小值,.
答:该公司最少花费2 600元.
C组·核心素养拓展 素养渗透
5.(1) ;
(2) 解:与之间的函数关系式为.
(3) 设甲、乙两种剪纸装饰获得的利润为元,
根据题意,得,即,
,随的增大而增大,
该商家计划购进这批剪纸装饰所花的总费用不超过2 800元,
,即,解得.
为非负整数, 当时,取得最大值,(元),
此时.
答:商家购进甲种剪纸装饰40套,乙种剪纸装饰20套时,所获利润最大,最大利润为800元.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
