1.1 等腰三角形 课堂检测(含答案)初中数学北师大版八年级下册
文档属性
| 名称 | 1.1 等腰三角形 课堂检测(含答案)初中数学北师大版八年级下册 | 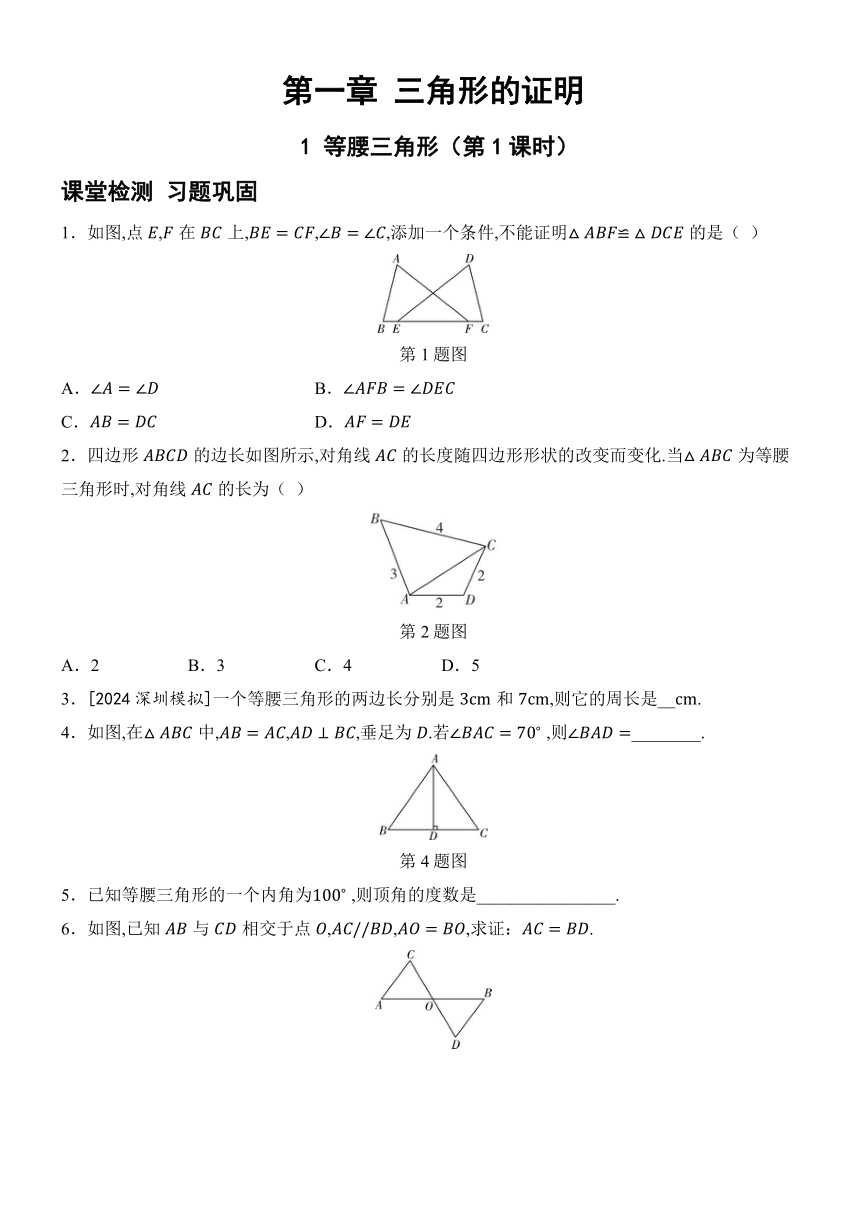 | |
| 格式 | docx | ||
| 文件大小 | 129.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 22:25:44 | ||
图片预览





文档简介
第一章 三角形的证明
1 等腰三角形(第1课时)
课堂检测 习题巩固
1.如图,点,在上,,,添加一个条件,不能证明的是( )
第1题图
A. B.
C. D.
2.四边形的边长如图所示,对角线的长度随四边形形状的改变而变化.当为等腰三角形时,对角线的长为( )
第2题图
A.2 B.3 C.4 D.5
3.[2024深圳模拟]一个等腰三角形的两边长分别是和,则它的周长是__.
4.如图,在中,,,垂足为.若 ,则________.
第4题图
5.已知等腰三角形的一个内角为 ,则顶角的度数是________________.
6.如图,已知与相交于点,,,求证:.
1 等腰三角形(第2课时)
课堂检测 习题巩固
1.[2024深圳模拟]已知为等边三角形,则的度数是( )
A. B. C. D.
2.[2023上海]下列说法中,错误的是( )
A.等腰三角形两腰上的高相等
B.等腰三角形两腰上的中线相等
C.等腰三角形两底角的平分线相等
D.等腰三角形高、中线和角平分线重合
3.如图,在等边三角形中,,分别是,边上的高,且,相交于点,则的度数为______________.
第3题图
4.如图,直线,过等边三角形的顶点和,且, ,则的度数为________________.
第4题图
5.如图,是等边三角形的中线,以点为圆心,的长为半径画弧,交的延长线于点,连接.求证:.
1 等腰三角形(第3课时)
课堂检测 习题巩固
1.如图,在等腰中,为的平分线, ,,,则的周长为( )
第1题图
A. B. C. D.
2.如图,在中,,, ,则图中等腰三角形共有( )
第2题图
A.3个 B.4个 C.5个 D.6个
3.如图,一艘船从处观测海岛在北偏东 方向,上午11时该船从处出发,以的速度沿正北方向航行到处,再观测海岛在北偏东 方向,且此时该船距离海岛,则该船到达处的时间为__时.
第3题图
4.以下是用反证法证明:等腰三角形的两底角必为锐角.请将过程补充完整.
证明:①假设等腰三角形的底角,都是直角,则________________,
从而________________ ,
这与____________________________矛盾;
②假设等腰三角形的底角,都是钝角,
则________________,从而______________________,
这与____________________________矛盾.
综上所述,假设①②__________,
,只能为____.
等腰三角形的两底角必为锐角.
5.[2024平顶山模拟]如图,在中,,是通过如图的作图痕迹作图而得,,交于点.
(1) 求证:;
(2) 若 ,则的度数是________.
1 等腰三角形(第4课时)
课堂检测 习题巩固
1.下列条件中,不能得到等边三角形的是( )
A.有两个内角是 的三角形
B.三边都相等的三角形
C.有一个角是 的等腰三角形
D.有两个外角相等的等腰三角形
2.2023年5月26日,“2023中国国际大数据产业博览会”在贵阳开幕,在“自动化立体库”中有许多几何元素,其中有一个等腰三角形模型(示意图如图所示),它的顶角为 ,腰长为,则底边上的高是( )
第2题图
A. B. C. D.
3.如图,在中, , ,是斜边上的高,,则的长是( )
第3题图
A. B. C. D.
4.如图,一棵树在一次强台风中于离地面处折断倒下,倒下部分与地面成 夹角,这棵树在折断前的高度为__.
第4题图
5.如图,,,.求证:是等边三角形.
1 等腰三角形(第1课时)
课堂探究 例题点拨
类型之一 全等三角形的判定公理和性质公理的应用
例1 证明:,
.
,
,即.
在和中,
.
.
『本题通过证明三角形全等得到对应边相等,综合考查了全等三角形的判定和性质.』
类型之二 等腰三角形的性质证明
例2 证明:方法一: 点是的中点,.
在和中,,.
方法二、方法三的证明略.
类型之三 等腰三角形的性质及三角形内角和定理的综合运用
例3 解: ,, .
是的中点,,是的垂直平分线,
, ,
.
课堂检测 习题巩固
1.D 2.B
3.17
4.
5.
6.证明:.
,.
在和中,
,
.
1 等腰三角形(第2课时)
课堂探究 例题点拨
类型之一 证明等腰三角形的有关结论
例1 证明:,,,
,.
在和中,
.
【变式】 证明:,,
.
在和中,
.
.
类型之二 等边三角形的性质
例2 证明:是等边三角形,
, ,
.
在和中,
.
『等边三角形的三个角都相等,三条边都相等,所以在证明三角形全等时要充分运用这些条件.全等三角形的判定常用方法有,,,等.』
课堂检测 习题巩固
1.C 2.D
3.
4.
5.证明:是等边三角形的中线,
, ,
.
, .
,
,
.
1 等腰三角形(第3课时)
课堂探究 例题点拨
类型之一 等腰三角形的判定定理的证明
例1 证明:方法一:根据题意,得.
在和中,,是等腰三角形.
方法二的证明略.
类型之二 等腰三角形的判定定理的运用
例2 (1) 证明:,
.
,是的两条高,
.
,,
是等腰三角形.
(2) 在和中,,.
类型之三 反证法的应用
例3 证明:假设是钝角或直角.
,是底边上的高,
.
是钝角或直角,
,不符合三角形内角和定理,
假设不成立,
是一个锐角.
课堂检测 习题巩固
1.A 2.D
3.13
4.; ; 三角形内角和为; ; ; 三角形内角和为; 均不成立; 锐角
5.(1) 证明:由作图可知,平分,
.
,,
,.
(2)
1 等腰三角形(第4课时)
课堂探究 例题点拨
类型之一 等边三角形的判定定理的证明
例1 证明:如答图,已知.
例1答图
①如果 ,那么 ,
,
,,,
是等边三角形;
②如果 ,同①得,是等边三角形;
③如果 ,
由 和,得 .
,,,
是等边三角形.
综上所述,有一个角等于 的等腰三角形是等边三角形.
类型之二 含30°角的直角三角形的性质定理
例2 方法一: 证明: , ,
, , .
,,,
是等边三角形,.
,.
方法二: 方法二的证明略.
类型之三 含30°角的直角三角形在实际生活中的应用
例3 解:如答图,过点作,垂足为.
根据题意,得 , ,
例3答图
,
,
.
在中,
,
,
该船一直向东航行有触礁的危险.
课堂检测 习题巩固
1.D 2.B 3.D
4.12
5.证明:,,
.
,.
,
是等边三角形.
1 等腰三角形(第1课时)
课堂检测 习题巩固
1.如图,点,在上,,,添加一个条件,不能证明的是( )
第1题图
A. B.
C. D.
2.四边形的边长如图所示,对角线的长度随四边形形状的改变而变化.当为等腰三角形时,对角线的长为( )
第2题图
A.2 B.3 C.4 D.5
3.[2024深圳模拟]一个等腰三角形的两边长分别是和,则它的周长是__.
4.如图,在中,,,垂足为.若 ,则________.
第4题图
5.已知等腰三角形的一个内角为 ,则顶角的度数是________________.
6.如图,已知与相交于点,,,求证:.
1 等腰三角形(第2课时)
课堂检测 习题巩固
1.[2024深圳模拟]已知为等边三角形,则的度数是( )
A. B. C. D.
2.[2023上海]下列说法中,错误的是( )
A.等腰三角形两腰上的高相等
B.等腰三角形两腰上的中线相等
C.等腰三角形两底角的平分线相等
D.等腰三角形高、中线和角平分线重合
3.如图,在等边三角形中,,分别是,边上的高,且,相交于点,则的度数为______________.
第3题图
4.如图,直线,过等边三角形的顶点和,且, ,则的度数为________________.
第4题图
5.如图,是等边三角形的中线,以点为圆心,的长为半径画弧,交的延长线于点,连接.求证:.
1 等腰三角形(第3课时)
课堂检测 习题巩固
1.如图,在等腰中,为的平分线, ,,,则的周长为( )
第1题图
A. B. C. D.
2.如图,在中,,, ,则图中等腰三角形共有( )
第2题图
A.3个 B.4个 C.5个 D.6个
3.如图,一艘船从处观测海岛在北偏东 方向,上午11时该船从处出发,以的速度沿正北方向航行到处,再观测海岛在北偏东 方向,且此时该船距离海岛,则该船到达处的时间为__时.
第3题图
4.以下是用反证法证明:等腰三角形的两底角必为锐角.请将过程补充完整.
证明:①假设等腰三角形的底角,都是直角,则________________,
从而________________ ,
这与____________________________矛盾;
②假设等腰三角形的底角,都是钝角,
则________________,从而______________________,
这与____________________________矛盾.
综上所述,假设①②__________,
,只能为____.
等腰三角形的两底角必为锐角.
5.[2024平顶山模拟]如图,在中,,是通过如图的作图痕迹作图而得,,交于点.
(1) 求证:;
(2) 若 ,则的度数是________.
1 等腰三角形(第4课时)
课堂检测 习题巩固
1.下列条件中,不能得到等边三角形的是( )
A.有两个内角是 的三角形
B.三边都相等的三角形
C.有一个角是 的等腰三角形
D.有两个外角相等的等腰三角形
2.2023年5月26日,“2023中国国际大数据产业博览会”在贵阳开幕,在“自动化立体库”中有许多几何元素,其中有一个等腰三角形模型(示意图如图所示),它的顶角为 ,腰长为,则底边上的高是( )
第2题图
A. B. C. D.
3.如图,在中, , ,是斜边上的高,,则的长是( )
第3题图
A. B. C. D.
4.如图,一棵树在一次强台风中于离地面处折断倒下,倒下部分与地面成 夹角,这棵树在折断前的高度为__.
第4题图
5.如图,,,.求证:是等边三角形.
1 等腰三角形(第1课时)
课堂探究 例题点拨
类型之一 全等三角形的判定公理和性质公理的应用
例1 证明:,
.
,
,即.
在和中,
.
.
『本题通过证明三角形全等得到对应边相等,综合考查了全等三角形的判定和性质.』
类型之二 等腰三角形的性质证明
例2 证明:方法一: 点是的中点,.
在和中,,.
方法二、方法三的证明略.
类型之三 等腰三角形的性质及三角形内角和定理的综合运用
例3 解: ,, .
是的中点,,是的垂直平分线,
, ,
.
课堂检测 习题巩固
1.D 2.B
3.17
4.
5.
6.证明:.
,.
在和中,
,
.
1 等腰三角形(第2课时)
课堂探究 例题点拨
类型之一 证明等腰三角形的有关结论
例1 证明:,,,
,.
在和中,
.
【变式】 证明:,,
.
在和中,
.
.
类型之二 等边三角形的性质
例2 证明:是等边三角形,
, ,
.
在和中,
.
『等边三角形的三个角都相等,三条边都相等,所以在证明三角形全等时要充分运用这些条件.全等三角形的判定常用方法有,,,等.』
课堂检测 习题巩固
1.C 2.D
3.
4.
5.证明:是等边三角形的中线,
, ,
.
, .
,
,
.
1 等腰三角形(第3课时)
课堂探究 例题点拨
类型之一 等腰三角形的判定定理的证明
例1 证明:方法一:根据题意,得.
在和中,,是等腰三角形.
方法二的证明略.
类型之二 等腰三角形的判定定理的运用
例2 (1) 证明:,
.
,是的两条高,
.
,,
是等腰三角形.
(2) 在和中,,.
类型之三 反证法的应用
例3 证明:假设是钝角或直角.
,是底边上的高,
.
是钝角或直角,
,不符合三角形内角和定理,
假设不成立,
是一个锐角.
课堂检测 习题巩固
1.A 2.D
3.13
4.; ; 三角形内角和为; ; ; 三角形内角和为; 均不成立; 锐角
5.(1) 证明:由作图可知,平分,
.
,,
,.
(2)
1 等腰三角形(第4课时)
课堂探究 例题点拨
类型之一 等边三角形的判定定理的证明
例1 证明:如答图,已知.
例1答图
①如果 ,那么 ,
,
,,,
是等边三角形;
②如果 ,同①得,是等边三角形;
③如果 ,
由 和,得 .
,,,
是等边三角形.
综上所述,有一个角等于 的等腰三角形是等边三角形.
类型之二 含30°角的直角三角形的性质定理
例2 方法一: 证明: , ,
, , .
,,,
是等边三角形,.
,.
方法二: 方法二的证明略.
类型之三 含30°角的直角三角形在实际生活中的应用
例3 解:如答图,过点作,垂足为.
根据题意,得 , ,
例3答图
,
,
.
在中,
,
,
该船一直向东航行有触礁的危险.
课堂检测 习题巩固
1.D 2.B 3.D
4.12
5.证明:,,
.
,.
,
是等边三角形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
