3.2 图形的旋转 课堂检测(含答案) 初中数学北师大版八年级下册
文档属性
| 名称 | 3.2 图形的旋转 课堂检测(含答案) 初中数学北师大版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 459.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 22:28:09 | ||
图片预览


文档简介
2 图形的旋转(第1课时)
课堂检测 习题巩固
1.将数字“6”旋转 ,得到数字“9”;将数字“9”旋转 ,得到数字“6”.现将数“69”旋转 ,得到的数是( )
A.96 B.69 C.66 D.99
2.如图,在的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
第2题图
A.格点 B.格点 C.格点 D.格点
3.如图,将绕点顺时针旋转 后得到.若 ,则的度数是( )
第3题图
A. B. C. D.
4.如图,一块直角三角板在水平桌面上绕点按顺时针方向旋转到的位置,使,,三点共线,那么旋转角的度数为________.
第4题图
5.[2024深圳模拟]如图,分别在的,两边上向外作正方形和正方形,连接,.问图中存在一个图形是由另一个图形绕某点按某个方向旋转某个角度所得吗?请说明你的理由.
2 图形的旋转(第2课时)
课堂检测 习题巩固
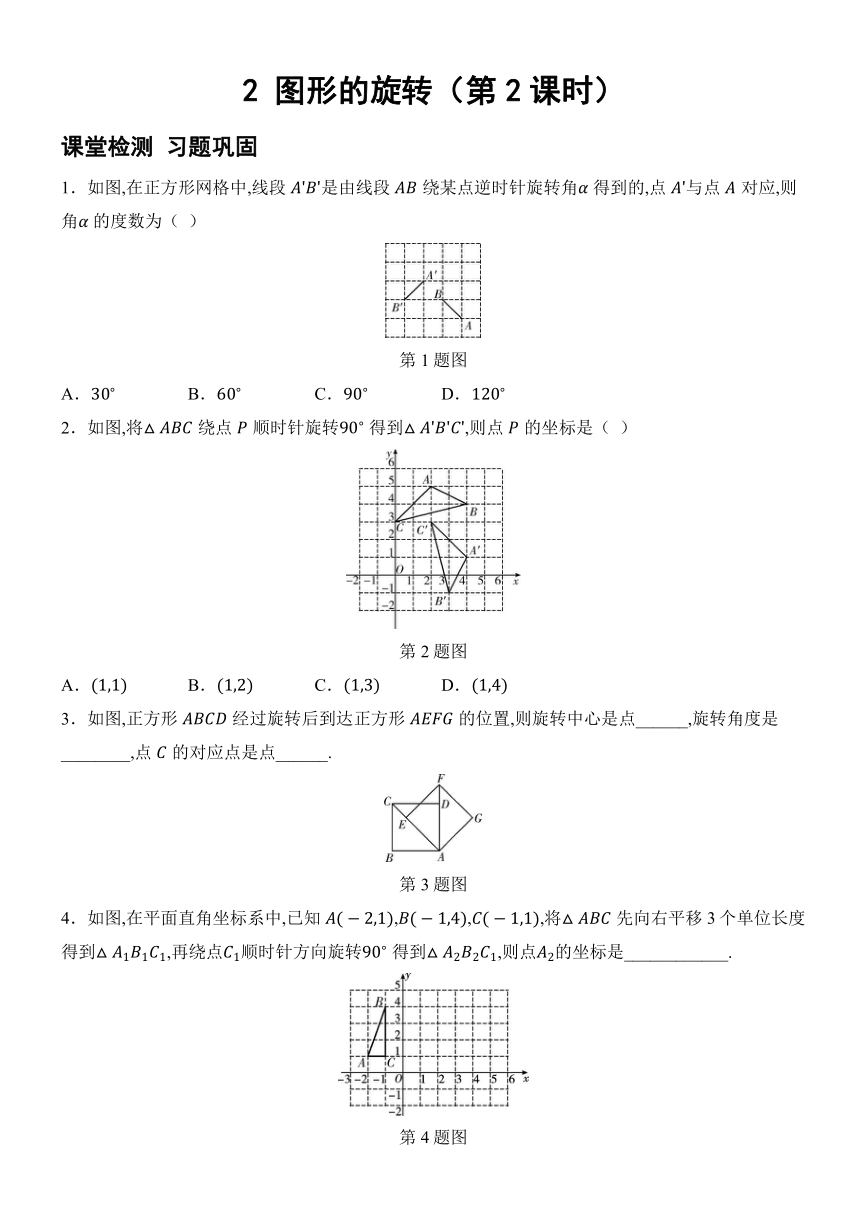
1.如图,在正方形网格中,线段是由线段绕某点逆时针旋转角 得到的,点与点对应,则角 的度数为( )
第1题图
A. B. C. D.
2.如图,将绕点顺时针旋转 得到,则点的坐标是( )
第2题图
A. B. C. D.
3.如图,正方形经过旋转后到达正方形的位置,则旋转中心是点______,旋转角度是________,点的对应点是点______.
第3题图
4.如图,在平面直角坐标系中,已知,,,将先向右平移3个单位长度得到,再绕点顺时针方向旋转 得到,则点的坐标是____________.
第4题图
5.如图,在平面直角坐标系中,的顶点坐标分别是,,.
(1) 将以点为旋转中心旋转 ,画出旋转后对应的;
(2) 将平移后得到,若点的对应点的坐标为,画出平移后对应的;
(3) 求线段的长度.
2 图形的旋转(第1课时)
课堂探究 例题点拨
类型之一 旋转及其性质
例1 (1) 解:由于旋转不改变图形的形状和大小,故.
(2) .
类型之二 分析旋转现象
例2 解:它可以看做是一个风叶通过五次旋转得到的,每次旋转了 ,还可以把连续的两个、三个或相对的两个风叶看成一个“基本图案”,经过两次、一次或两次旋转得到,有多种旋转方式.
类型之三 旋转的应用
例3 (1) 解:,且.理由略.
(2) .
课堂检测 习题巩固
1.B 2.B 3.B
4.
5.解:存在.理由如下:
根据正方形的性质可得:,, ,
,
,
故可看作绕点逆时针旋转 得到.
2 图形的旋转(第2课时)
课堂探究 例题点拨
类型之一 旋转作图
例1 解:如答图,四边形即为所求作.
例1答图
类型之二 在平面直角坐标系中或网格图中作旋转图形
『利用旋转变换作图,熟练掌握网格结构,准确找出对应点的位置是解题的关键.』
例2 (1) 解:如答图,即为所求作.
例2答图
(2) 如答图,即为所求作.
例2答图
课堂检测 习题巩固
1.C 2.B
3.; ;
4.
5.(1) 解:如答图,即为所求作.
第5题答图
(2) 如答图,即为所求作.
第5题答图
(3) 由(1)与(2)可得 ,,作轴于点(图略),
则,,,
根据勾股定理,得.
课堂检测 习题巩固
1.将数字“6”旋转 ,得到数字“9”;将数字“9”旋转 ,得到数字“6”.现将数“69”旋转 ,得到的数是( )
A.96 B.69 C.66 D.99
2.如图,在的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
第2题图
A.格点 B.格点 C.格点 D.格点
3.如图,将绕点顺时针旋转 后得到.若 ,则的度数是( )
第3题图
A. B. C. D.
4.如图,一块直角三角板在水平桌面上绕点按顺时针方向旋转到的位置,使,,三点共线,那么旋转角的度数为________.
第4题图
5.[2024深圳模拟]如图,分别在的,两边上向外作正方形和正方形,连接,.问图中存在一个图形是由另一个图形绕某点按某个方向旋转某个角度所得吗?请说明你的理由.
2 图形的旋转(第2课时)
课堂检测 习题巩固
1.如图,在正方形网格中,线段是由线段绕某点逆时针旋转角 得到的,点与点对应,则角 的度数为( )
第1题图
A. B. C. D.
2.如图,将绕点顺时针旋转 得到,则点的坐标是( )
第2题图
A. B. C. D.
3.如图,正方形经过旋转后到达正方形的位置,则旋转中心是点______,旋转角度是________,点的对应点是点______.
第3题图
4.如图,在平面直角坐标系中,已知,,,将先向右平移3个单位长度得到,再绕点顺时针方向旋转 得到,则点的坐标是____________.
第4题图
5.如图,在平面直角坐标系中,的顶点坐标分别是,,.
(1) 将以点为旋转中心旋转 ,画出旋转后对应的;
(2) 将平移后得到,若点的对应点的坐标为,画出平移后对应的;
(3) 求线段的长度.
2 图形的旋转(第1课时)
课堂探究 例题点拨
类型之一 旋转及其性质
例1 (1) 解:由于旋转不改变图形的形状和大小,故.
(2) .
类型之二 分析旋转现象
例2 解:它可以看做是一个风叶通过五次旋转得到的,每次旋转了 ,还可以把连续的两个、三个或相对的两个风叶看成一个“基本图案”,经过两次、一次或两次旋转得到,有多种旋转方式.
类型之三 旋转的应用
例3 (1) 解:,且.理由略.
(2) .
课堂检测 习题巩固
1.B 2.B 3.B
4.
5.解:存在.理由如下:
根据正方形的性质可得:,, ,
,
,
故可看作绕点逆时针旋转 得到.
2 图形的旋转(第2课时)
课堂探究 例题点拨
类型之一 旋转作图
例1 解:如答图,四边形即为所求作.
例1答图
类型之二 在平面直角坐标系中或网格图中作旋转图形
『利用旋转变换作图,熟练掌握网格结构,准确找出对应点的位置是解题的关键.』
例2 (1) 解:如答图,即为所求作.
例2答图
(2) 如答图,即为所求作.
例2答图
课堂检测 习题巩固
1.C 2.B
3.; ;
4.
5.(1) 解:如答图,即为所求作.
第5题答图
(2) 如答图,即为所求作.
第5题答图
(3) 由(1)与(2)可得 ,,作轴于点(图略),
则,,,
根据勾股定理,得.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
