第六章 平行四边形 质量评估(含答案)初中数学北师大版八年级下册
文档属性
| 名称 | 第六章 平行四边形 质量评估(含答案)初中数学北师大版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 240.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-08 00:00:00 | ||
图片预览



文档简介
第六章 平行四边形 质量评估
[时间:90分钟 分值:100分]
第一部分 选择题
一、选择题(本大题共8个小题,每小题3分,共24分,每小题有四个选项,其中只有一个是正确的)
1.如图,在中,,,则的周长为( )
第1题图
A.6 B.8 C.12 D.14
2.一个正多边形的内角和等于 ,则这个正多边形的每个外角等于( )
A. B. C. D.
3.如图,小张想估测被池塘隔开的,两处景观之间的距离,他先在外取一点,然后步测出,的中点,,并步测出的长约为,由此估测,之间的距离约为( )
第3题图
A. B. C. D.
4.过多边形一个顶点的所有对角线,将这个多边形分为5个三角形,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
5.如图,在中,对角线,相交于点,点是的中点.若,则的长为( )
第5题图
A.16 B.18 C.20 D.22
6.如图,的对角线,相交于点,,.若,,则四边形的周长为( )
第6题图
A.4 B.6 C.8 D.16
7.如图,在中,对角线,相交于点,,是对角线上的两点,下列条件中,不一定能使四边形是平行四边形的是( )
第7题图
A. B.
C. D.
8.如图,在中, ,,,点在上,以为对角线的所有中,的最小值是( )
第8题图
A.2 B.3 C.4 D.5
第二部分 非选择题
二、填空题(本大题共5个小题,每小题3分,共15分)
9.图①是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消融,形状无一定规则,代表一种自然和谐美.图②是从图①冰裂纹窗格图案中提取的由五条线段组成的图形,则____________.
第9题图
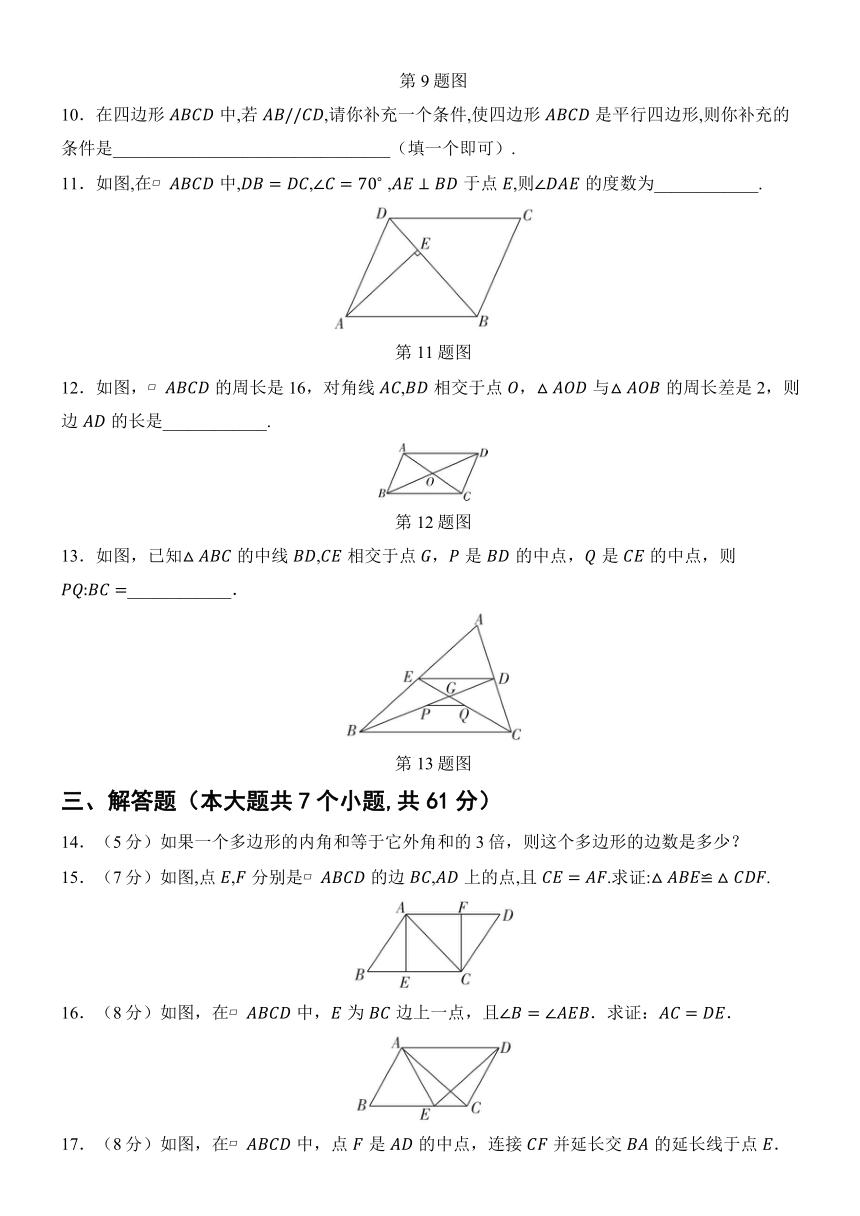
10.在四边形中,若,请你补充一个条件,使四边形是平行四边形,则你补充的条件是________________________________(填一个即可).
11.如图,在中,, ,于点,则的度数为____________.
第11题图
12.如图,的周长是16,对角线,相交于点,与的周长差是2,则边的长是____________.
第12题图
13.如图,已知的中线,相交于点,是的中点,是的中点,则____________.
第13题图
三、解答题(本大题共7个小题,共61分)
14.(5分)如果一个多边形的内角和等于它外角和的3倍,则这个多边形的边数是多少?
15.(7分)如图,点,分别是的边,上的点,且.求证:.
16.(8分)如图,在中,为边上一点,且.求证:.
17.(8分)如图,在中,点是的中点,连接并延长交的延长线于点.
(1) 求证:;
(2) 若, ,求的度数.
18.(9分)如图,线段,相交于点,且,于点.
(1) 尺规作图:过点作的垂线,垂足为,连接,;(不写作法,保留作图痕迹,并标明相应的字母)
(2) 若,请判断四边形的形状,并说明理由.(若前问未完成,可画草图完成此问)
19.(12分)如图,在中,垂直平分,交于点,连接,过点作,交的延长线于点,连接.
(1) 求证:四边形是平行四边形;
(2) 若,,,求的长.
20.(12分)如图,在四边形中,, ,,,,点从点出发以的速度沿运动,点从点出发的同时点从点出发,以的速度沿向点运动,当点到达点时,点也停止运动.设点,运动的时间为.
(1) 从运动开始,当取何值时,四边形是平行四边形?
(2) 在运动过程中,是否存在以为腰的等腰三角形?若存在,求出的值;若不存在,请说明理由.
第六章质量评估
第一部分 选择题
一、选择题(本大题共8个小题,每小题3分,共24分,每小题有四个选项,其中只有一个是正确的)
1.C
2.A
3.C
4.C
5.A
6.C
7.A
8.B
[解析] 四边形是平行四边形,
,,.
当时,最小(平行线之间垂线段最短),此时.
又 点为的中点,是的中位线.
,.故选B.
第二部分 非选择题
二、填空题(本大题共5个小题,每小题3分,共15分)
9.
10.(答案不唯一)
11.
[解析], ,
.
,,
, .
.
12.或3
13.
三、解答题(本大题共7个小题,共61分)
14.解:设多边形的边数是.
根据题意,得 ,
解得.
答:这个多边形的边数是8.
15.证明: 四边形是平行四边形,
,,.
,
,
.
在和中,
.
16.证明: 四边形是平行四边形,
,,.
,,.
在和中,
,.
17.(1) 证明: 四边形是平行四边形,
,,,.
点是的中点,.
在和中,
,
,.
(2) 解:由(1)可得,.
,.
, , .
18.(1) 解:如答图,,,即为所求作.
第18题答图
(2) 四边形是平行四边形.理由如下:
,.
,,, .
在和中,
,.
, 四边形是平行四边形.
19.(1) 证明:垂直平分,.
,,,
,,
四边形是平行四边形.
(2) 解:由(1)可知,四边形是平行四边形,
,.
垂直平分, ,
,
.
即的长为.
20.(1) 解:当时,四边形是平行四边形,此时,
,解得.
当时,四边形是平行四边形.
(2) 存在.如答图,过点作于点.
第20题答图
根据题意,得,.
根据勾股定理,得.
根据题意,得且,
解得.
当时,;
当时,,(不合题意,舍去).
综上所述,存在以为腰的等腰三角形,此时,的值为10.
[时间:90分钟 分值:100分]
第一部分 选择题
一、选择题(本大题共8个小题,每小题3分,共24分,每小题有四个选项,其中只有一个是正确的)
1.如图,在中,,,则的周长为( )
第1题图
A.6 B.8 C.12 D.14
2.一个正多边形的内角和等于 ,则这个正多边形的每个外角等于( )
A. B. C. D.
3.如图,小张想估测被池塘隔开的,两处景观之间的距离,他先在外取一点,然后步测出,的中点,,并步测出的长约为,由此估测,之间的距离约为( )
第3题图
A. B. C. D.
4.过多边形一个顶点的所有对角线,将这个多边形分为5个三角形,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
5.如图,在中,对角线,相交于点,点是的中点.若,则的长为( )
第5题图
A.16 B.18 C.20 D.22
6.如图,的对角线,相交于点,,.若,,则四边形的周长为( )
第6题图
A.4 B.6 C.8 D.16
7.如图,在中,对角线,相交于点,,是对角线上的两点,下列条件中,不一定能使四边形是平行四边形的是( )
第7题图
A. B.
C. D.
8.如图,在中, ,,,点在上,以为对角线的所有中,的最小值是( )
第8题图
A.2 B.3 C.4 D.5
第二部分 非选择题
二、填空题(本大题共5个小题,每小题3分,共15分)
9.图①是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消融,形状无一定规则,代表一种自然和谐美.图②是从图①冰裂纹窗格图案中提取的由五条线段组成的图形,则____________.
第9题图
10.在四边形中,若,请你补充一个条件,使四边形是平行四边形,则你补充的条件是________________________________(填一个即可).
11.如图,在中,, ,于点,则的度数为____________.
第11题图
12.如图,的周长是16,对角线,相交于点,与的周长差是2,则边的长是____________.
第12题图
13.如图,已知的中线,相交于点,是的中点,是的中点,则____________.
第13题图
三、解答题(本大题共7个小题,共61分)
14.(5分)如果一个多边形的内角和等于它外角和的3倍,则这个多边形的边数是多少?
15.(7分)如图,点,分别是的边,上的点,且.求证:.
16.(8分)如图,在中,为边上一点,且.求证:.
17.(8分)如图,在中,点是的中点,连接并延长交的延长线于点.
(1) 求证:;
(2) 若, ,求的度数.
18.(9分)如图,线段,相交于点,且,于点.
(1) 尺规作图:过点作的垂线,垂足为,连接,;(不写作法,保留作图痕迹,并标明相应的字母)
(2) 若,请判断四边形的形状,并说明理由.(若前问未完成,可画草图完成此问)
19.(12分)如图,在中,垂直平分,交于点,连接,过点作,交的延长线于点,连接.
(1) 求证:四边形是平行四边形;
(2) 若,,,求的长.
20.(12分)如图,在四边形中,, ,,,,点从点出发以的速度沿运动,点从点出发的同时点从点出发,以的速度沿向点运动,当点到达点时,点也停止运动.设点,运动的时间为.
(1) 从运动开始,当取何值时,四边形是平行四边形?
(2) 在运动过程中,是否存在以为腰的等腰三角形?若存在,求出的值;若不存在,请说明理由.
第六章质量评估
第一部分 选择题
一、选择题(本大题共8个小题,每小题3分,共24分,每小题有四个选项,其中只有一个是正确的)
1.C
2.A
3.C
4.C
5.A
6.C
7.A
8.B
[解析] 四边形是平行四边形,
,,.
当时,最小(平行线之间垂线段最短),此时.
又 点为的中点,是的中位线.
,.故选B.
第二部分 非选择题
二、填空题(本大题共5个小题,每小题3分,共15分)
9.
10.(答案不唯一)
11.
[解析], ,
.
,,
, .
.
12.或3
13.
三、解答题(本大题共7个小题,共61分)
14.解:设多边形的边数是.
根据题意,得 ,
解得.
答:这个多边形的边数是8.
15.证明: 四边形是平行四边形,
,,.
,
,
.
在和中,
.
16.证明: 四边形是平行四边形,
,,.
,,.
在和中,
,.
17.(1) 证明: 四边形是平行四边形,
,,,.
点是的中点,.
在和中,
,
,.
(2) 解:由(1)可得,.
,.
, , .
18.(1) 解:如答图,,,即为所求作.
第18题答图
(2) 四边形是平行四边形.理由如下:
,.
,,, .
在和中,
,.
, 四边形是平行四边形.
19.(1) 证明:垂直平分,.
,,,
,,
四边形是平行四边形.
(2) 解:由(1)可知,四边形是平行四边形,
,.
垂直平分, ,
,
.
即的长为.
20.(1) 解:当时,四边形是平行四边形,此时,
,解得.
当时,四边形是平行四边形.
(2) 存在.如答图,过点作于点.
第20题答图
根据题意,得,.
根据勾股定理,得.
根据题意,得且,
解得.
当时,;
当时,,(不合题意,舍去).
综上所述,存在以为腰的等腰三角形,此时,的值为10.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
