山东省嘉祥县大张楼镇第一中学人教版九年级数学上册课件22.1.2 二次函数y=a(x-h)2+k的图像与性质(共27张PPT)
文档属性
| 名称 | 山东省嘉祥县大张楼镇第一中学人教版九年级数学上册课件22.1.2 二次函数y=a(x-h)2+k的图像与性质(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 378.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-01 00:00:00 | ||
图片预览




文档简介
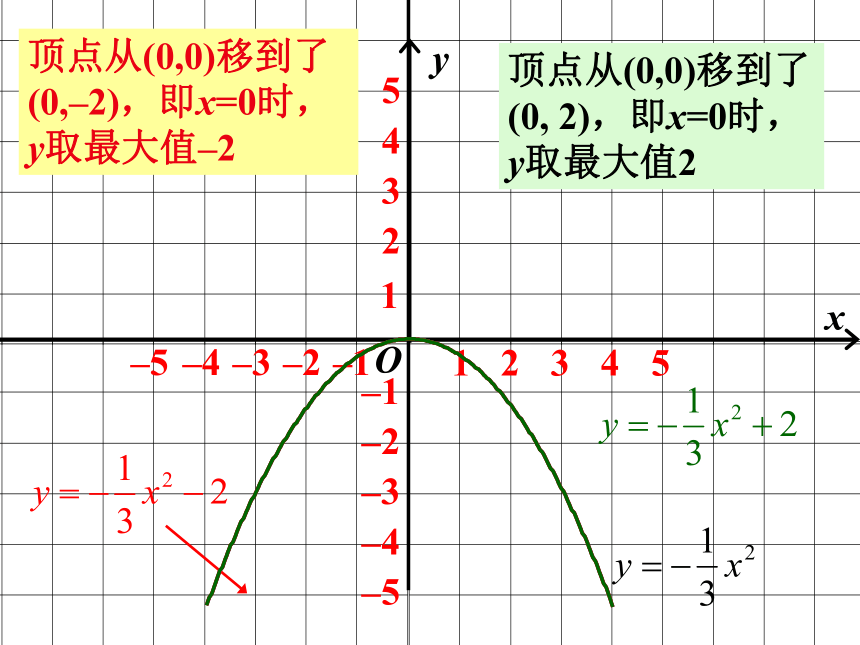
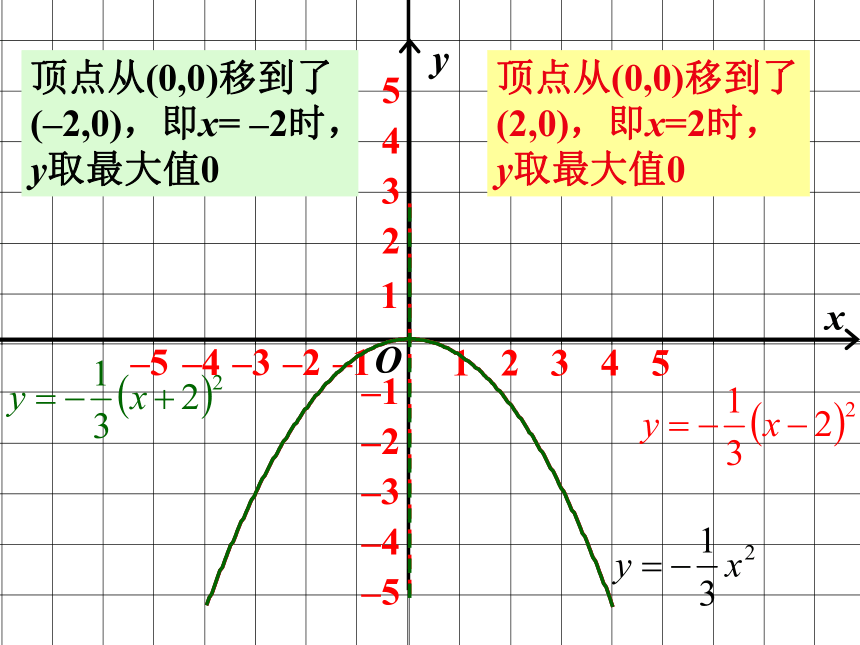
课件27张PPT。二次函数y=a(x-h)2+k的图象及其性质最新人教版九年级上册数学二次函数y=a(x–h)2的图象和性质. 当h>0时,向左平移当h<0时,向右平移y=ax2y=a(x–h)2复习回顾1.如何同y=-x2的图象得到y=-x2-3的图象。并说明后者图象的顶点,对称轴,增减性。2.如何y=2x2的图象得到y=2(x-3)2的图象。并说明后者图象的顶点,对称轴,增减性。y顶点从(0,0)移到了(0,–2),即x=0时,y取最大值–2顶点从(0,0)移到了(0, 2),即x=0时,y取最大值2y顶点从(0,0)移到了(2,0),即x=2时, y取最大值0顶点从(0,0)移到了(–2,0),即x= –2时,y取最大值01 说出下列函数图象的开口方向,对称轴,顶点,最值和增减变化情况:回忆一下1)y=ax2
2)y=ax2+c
3)y=a(x-h)2
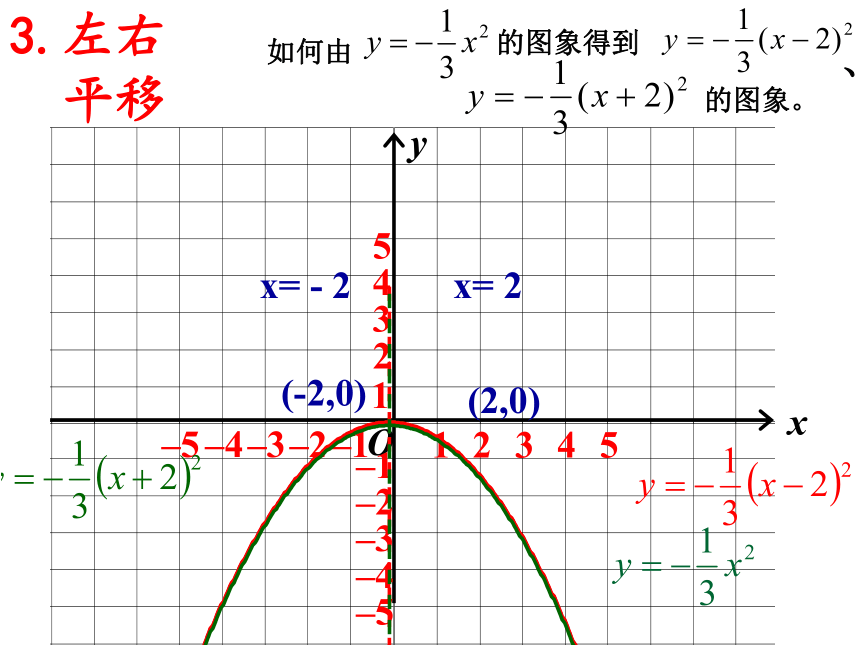
x= - 2(-2,0)(2,0)x= 2如何由 的图象得到 的图象。、3.左右
平移5.二次函数y=ax2
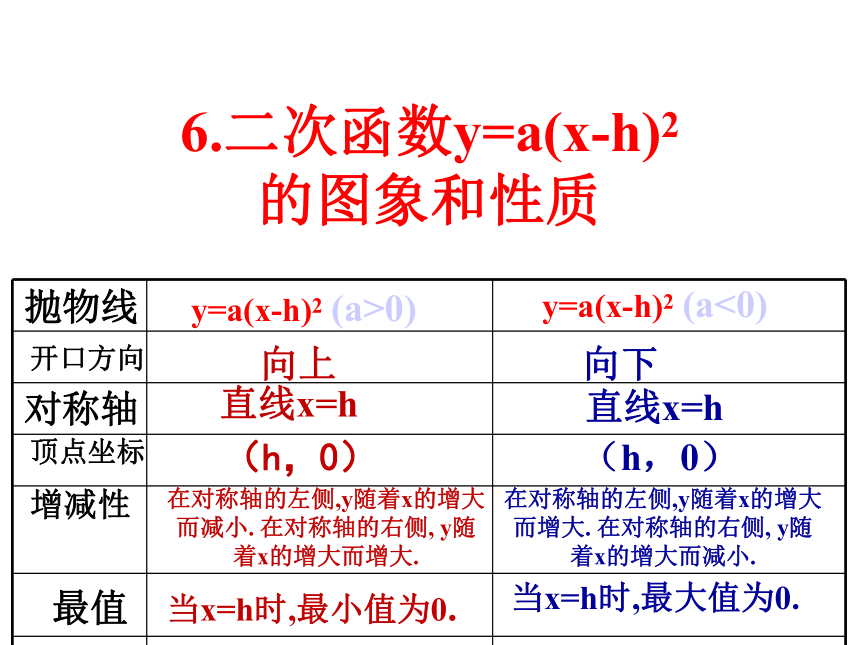
的图象和性质抛物线顶点坐标对称轴开口方向增减性最值y=ax2(a>0)y=ax2(a<0)(0,0)(0,0)直线x=0直线x=0向上向下当x=0时,最小值为0.当x=0时,最大值为0.在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 6.二次函数y=a(x-h)2
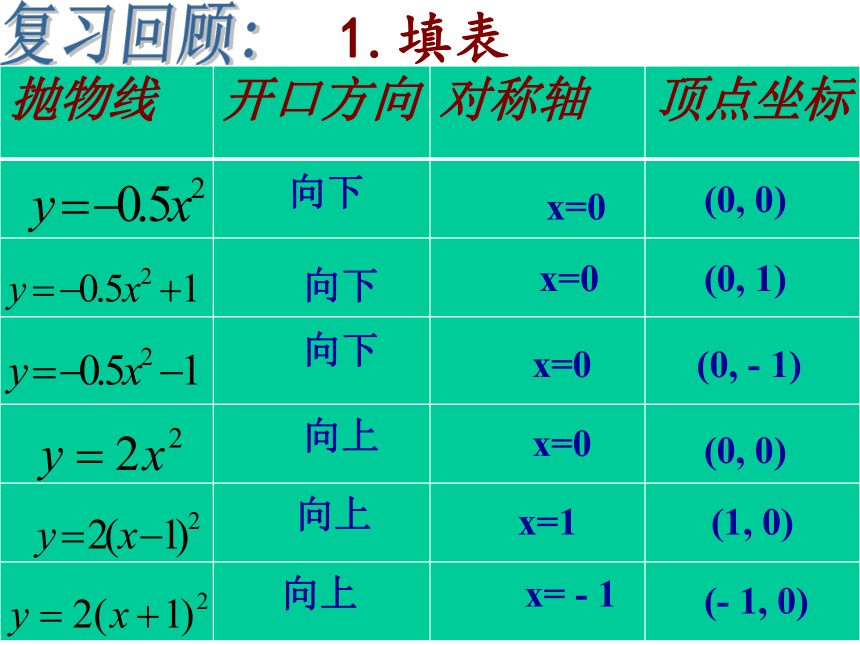
的图象和性质抛物线顶点坐标对称轴开口方向增减性最值y=a(x-h)2 (a>0)y=a(x-h)2 (a<0)(h,0)(h,0)直线x=h直线x=h向上向下当x=h时,最小值为0.当x=h时,最大值为0.在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 1.填表复习回顾:(0, 0)(1, 0)(- 1, 0)(0, 0)(0, 1)(0, - 1)向下向下向下向上向上向上x=0x=0x=0x=0x=1x= - 1将抛物线y=ax2沿y轴方向平移c个单位,得抛物线 y =ax2+c
将抛物线y=ax2沿x轴方向平移h个单位,得抛物线
y=a(x-h)2返回3 请说出二次函数y=2(x-3)2与抛物线y=2(x+3)2如何由y=2x2 平移而来2 请说出二次函数y=ax2+c与y=ax2的平移关系。
y=a(x-h)2与y=ax2的平移关系y=2x2y=2(x–1)2y=2(x–1)2+1在同一坐标系内画出y=2x2、y=2(x-1)2、 y=2(x-1)2+1 的图象的图像可以由向上平移一个单位向右平移一个单位向右平移一个单位向上平移
一个单位先向上平移一个单位,再向右平移一个单位,或者先向右平移一个单位再向上平移一个单位而得到.平移的规律总结:y=ax2y=a(x-h)2 y=a(x-h)2+k 当h>0时,向右平移h个单位当h<0时,向左平移 个单位当k>0时,向上平移k个单位当k<0时,向下平移 个单位联系:
将函数 y=2x2的图象向右平移1个 单位, 就得到
y=2(x-1)2的图象;
在向上平移2个单位, 得到函数 y=2(x-1)2+1的图象.
相同点: (1)图像都是抛物线, 形状相同, 开口方向相同.
(2)都是轴对称图形.
(3)顶点都是最低点.
(4) 在对称轴左侧,都随 x 的增大而减小,在对称轴右侧,都随 x 的增大而增大.
(5)它们的增长速度相同.
不同点: (1)对称轴不同. (2)顶点不同. (3)最小值不相同.观察
的图像x=-2(-2,2)(-2,-3)抛物线顶点坐标对称轴开口
方向增减性最值(-2,2)(2,-3)直线x=-2直线x=2向上向下当x=-2时,
最小值为2当x=2时,
最大值为-3在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. |a|越大开口越小.返回二次函数y=a(x-h)2+k的图象特征指出下列函数图象的开口方向,对称轴和顶点坐标.开口 对称轴 顶点坐标向上直线x=3(3,–5)向下直线x= –1(–1,0)向下直线x=0(0,–1)向上直线x=2(2, 5)向上直线x= – 4(– 4,2)向下直线x=3(3,0)练习1:指出下面函数的开口方向,对称轴,顶点坐标,最值。
1) y=2(x+3)2+5 2) y=4(x-3)2+7
3) y=-3(x-1)2-2 4) y=-5(x+2)2-6
练习2:对称轴是直线x=-2的抛物线是( )
A y=-2x2-2 B y=2x2-2
C y=-1/2(x+2)2-2 D y=-5(x-2)2-6C牛刀小试1. 抛物线的顶点为(3,5) 此抛物线的解析式可设为( )
Ay=a(x+3)2+5 By=a(x-3)2+5
Cy=a(x-3)2-5 Dy=a(x+3)2-5
2.抛物线c1的解析式为y=2(x-1)2+3抛物线c2与抛物线c1关于x轴对称,请直接写出抛物线c2的解析式_____活学活用你答对了吗?
1.B
2.y=-2(x-1)2-3
考点训练6.已知二次函数y=ax2+bx+c的图象如图所示
(1)求解析式
(2)何时 y=3?
(3)根据图象回答:
当x 时,y>0。3.二次函数y=a(x-m)2+2m,无论m为何实数,图象的顶点必在( )上
A)直线y=-2x上 B)x轴上 C)y轴上 D)直线y=2x上
4.对于抛物线y=a(x-3)2+b其中a>0,b 为常数,点( ,y1) 点( ,y2)点(8,y3)在该抛物线上,试比较y1,y2,y3的大小活学活用你答对了吗?
3.D
4. y3> y1 > y2
4.如图所示的抛物线:
当x=_____时,y=0;
当x<-2或x>0时, y_____0;
当x在 _____ 范围内时,y>0;
当x=_____时,y有最大值_____.
3 0或-2<-2 < x<0-135、试分别说明将抛物线的图象通过怎样的平移得到y=x2的图象:
(1) y=(x-3)2+2 ;
(2)y=(x+4)2-512.与抛物线y=-4x 2形状相同,顶点为(2,-3)的抛物线解析式为 .先向左平移3个单位,再向下平移2个单位先向右平移4个单位,再向上平移5个单位y= - 4(x-2)2-3或y= 4(x-2)2-36.已知二次函数y=ax2+bx+c的图象如图所示
(1)求解析式(1,-1)(0,0)(2,0) 当x 时,y﹤0。当x 时,y=0;(2)根据图象回答:
当x 时,y>0;解:∵二次函数图象的顶点是(1,-1),
∴设抛物线解析式是y=a(x-1)2-1,
∵其图象过点(0,0),
∴0= a(0-1)2-1,
∴a=1
∴y= (x-1)2-1x<0或x>20< x<2x=0或2延伸题1)若抛物线y=-x2向左平移2个单位,再向下平移4个单位所得抛物线的解析式是________
2)如何将抛物线y=2(x-1) 2+3经过平移得到抛物线y=2x2
3) 将抛 物线y=2(x -1)2+3经过怎样的平移得到抛物线y=2(x+2)2-1
4). 若抛物线y=2(x-1)2+3沿x轴方向平移后,经过(3,5),求平移后的抛物线的解析式_______
重点把握小结顶点y=a(x-h)2+k(h,k)对称轴直线 x=h最值 当a>0时
当a<0时x=h时,y有最小值kx=h时,y有最大值k
2)y=ax2+c
3)y=a(x-h)2
x= - 2(-2,0)(2,0)x= 2如何由 的图象得到 的图象。、3.左右
平移5.二次函数y=ax2
的图象和性质抛物线顶点坐标对称轴开口方向增减性最值y=ax2(a>0)y=ax2(a<0)(0,0)(0,0)直线x=0直线x=0向上向下当x=0时,最小值为0.当x=0时,最大值为0.在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 6.二次函数y=a(x-h)2
的图象和性质抛物线顶点坐标对称轴开口方向增减性最值y=a(x-h)2 (a>0)y=a(x-h)2 (a<0)(h,0)(h,0)直线x=h直线x=h向上向下当x=h时,最小值为0.当x=h时,最大值为0.在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 1.填表复习回顾:(0, 0)(1, 0)(- 1, 0)(0, 0)(0, 1)(0, - 1)向下向下向下向上向上向上x=0x=0x=0x=0x=1x= - 1将抛物线y=ax2沿y轴方向平移c个单位,得抛物线 y =ax2+c
将抛物线y=ax2沿x轴方向平移h个单位,得抛物线
y=a(x-h)2返回3 请说出二次函数y=2(x-3)2与抛物线y=2(x+3)2如何由y=2x2 平移而来2 请说出二次函数y=ax2+c与y=ax2的平移关系。
y=a(x-h)2与y=ax2的平移关系y=2x2y=2(x–1)2y=2(x–1)2+1在同一坐标系内画出y=2x2、y=2(x-1)2、 y=2(x-1)2+1 的图象的图像可以由向上平移一个单位向右平移一个单位向右平移一个单位向上平移
一个单位先向上平移一个单位,再向右平移一个单位,或者先向右平移一个单位再向上平移一个单位而得到.平移的规律总结:y=ax2y=a(x-h)2 y=a(x-h)2+k 当h>0时,向右平移h个单位当h<0时,向左平移 个单位当k>0时,向上平移k个单位当k<0时,向下平移 个单位联系:
将函数 y=2x2的图象向右平移1个 单位, 就得到
y=2(x-1)2的图象;
在向上平移2个单位, 得到函数 y=2(x-1)2+1的图象.
相同点: (1)图像都是抛物线, 形状相同, 开口方向相同.
(2)都是轴对称图形.
(3)顶点都是最低点.
(4) 在对称轴左侧,都随 x 的增大而减小,在对称轴右侧,都随 x 的增大而增大.
(5)它们的增长速度相同.
不同点: (1)对称轴不同. (2)顶点不同. (3)最小值不相同.观察
的图像x=-2(-2,2)(-2,-3)抛物线顶点坐标对称轴开口
方向增减性最值(-2,2)(2,-3)直线x=-2直线x=2向上向下当x=-2时,
最小值为2当x=2时,
最大值为-3在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. |a|越大开口越小.返回二次函数y=a(x-h)2+k的图象特征指出下列函数图象的开口方向,对称轴和顶点坐标.开口 对称轴 顶点坐标向上直线x=3(3,–5)向下直线x= –1(–1,0)向下直线x=0(0,–1)向上直线x=2(2, 5)向上直线x= – 4(– 4,2)向下直线x=3(3,0)练习1:指出下面函数的开口方向,对称轴,顶点坐标,最值。
1) y=2(x+3)2+5 2) y=4(x-3)2+7
3) y=-3(x-1)2-2 4) y=-5(x+2)2-6
练习2:对称轴是直线x=-2的抛物线是( )
A y=-2x2-2 B y=2x2-2
C y=-1/2(x+2)2-2 D y=-5(x-2)2-6C牛刀小试1. 抛物线的顶点为(3,5) 此抛物线的解析式可设为( )
Ay=a(x+3)2+5 By=a(x-3)2+5
Cy=a(x-3)2-5 Dy=a(x+3)2-5
2.抛物线c1的解析式为y=2(x-1)2+3抛物线c2与抛物线c1关于x轴对称,请直接写出抛物线c2的解析式_____活学活用你答对了吗?
1.B
2.y=-2(x-1)2-3
考点训练6.已知二次函数y=ax2+bx+c的图象如图所示
(1)求解析式
(2)何时 y=3?
(3)根据图象回答:
当x 时,y>0。3.二次函数y=a(x-m)2+2m,无论m为何实数,图象的顶点必在( )上
A)直线y=-2x上 B)x轴上 C)y轴上 D)直线y=2x上
4.对于抛物线y=a(x-3)2+b其中a>0,b 为常数,点( ,y1) 点( ,y2)点(8,y3)在该抛物线上,试比较y1,y2,y3的大小活学活用你答对了吗?
3.D
4. y3> y1 > y2
4.如图所示的抛物线:
当x=_____时,y=0;
当x<-2或x>0时, y_____0;
当x在 _____ 范围内时,y>0;
当x=_____时,y有最大值_____.
3 0或-2<-2 < x<0-135、试分别说明将抛物线的图象通过怎样的平移得到y=x2的图象:
(1) y=(x-3)2+2 ;
(2)y=(x+4)2-512.与抛物线y=-4x 2形状相同,顶点为(2,-3)的抛物线解析式为 .先向左平移3个单位,再向下平移2个单位先向右平移4个单位,再向上平移5个单位y= - 4(x-2)2-3或y= 4(x-2)2-36.已知二次函数y=ax2+bx+c的图象如图所示
(1)求解析式(1,-1)(0,0)(2,0) 当x 时,y﹤0。当x 时,y=0;(2)根据图象回答:
当x 时,y>0;解:∵二次函数图象的顶点是(1,-1),
∴设抛物线解析式是y=a(x-1)2-1,
∵其图象过点(0,0),
∴0= a(0-1)2-1,
∴a=1
∴y= (x-1)2-1x<0或x>20< x<2x=0或2延伸题1)若抛物线y=-x2向左平移2个单位,再向下平移4个单位所得抛物线的解析式是________
2)如何将抛物线y=2(x-1) 2+3经过平移得到抛物线y=2x2
3) 将抛 物线y=2(x -1)2+3经过怎样的平移得到抛物线y=2(x+2)2-1
4). 若抛物线y=2(x-1)2+3沿x轴方向平移后,经过(3,5),求平移后的抛物线的解析式_______
重点把握小结顶点y=a(x-h)2+k(h,k)对称轴直线 x=h最值 当a>0时
当a<0时x=h时,y有最小值kx=h时,y有最大值k
同课章节目录
