2024-2025学年华师大版数学九年级上册 第24章 解直角三角形 基础复习(一)(含答案)
文档属性
| 名称 | 2024-2025学年华师大版数学九年级上册 第24章 解直角三角形 基础复习(一)(含答案) | 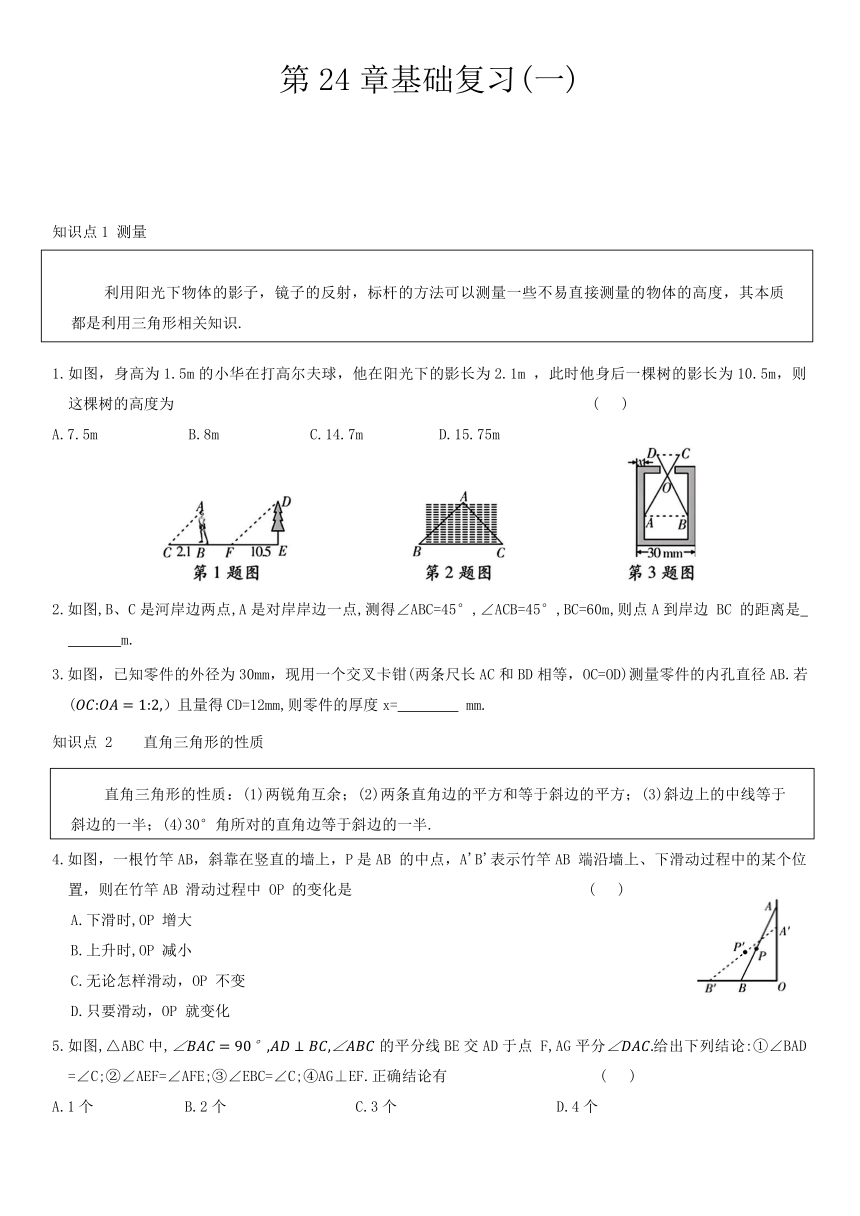 | |
| 格式 | docx | ||
| 文件大小 | 380.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 22:55:55 | ||
图片预览



文档简介
第24章基础复习(一)
知识点1 测量
利用阳光下物体的影子,镜子的反射,标杆的方法可以测量一些不易直接测量的物体的高度,其本质都是利用三角形相关知识.
1.如图,身高为1.5m的小华在打高尔夫球,他在阳光下的影长为2.1m ,此时他身后一棵树的影长为10.5m,则这棵树的高度为 ( )
A.7.5m B.8m C.14.7m D.15.75m
2.如图,B、C是河岸边两点,A是对岸岸边一点,测得∠ABC=45°,∠ACB=45°,BC=60m,则点A到岸边 BC 的距离是 m.
3.如图,已知零件的外径为30mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)测量零件的内孔直径AB.若()且量得CD=12mm,则零件的厚度x= mm.
知识点 2 直角三角形的性质
直角三角形的性质:(1)两锐角互余;(2)两条直角边的平方和等于斜边的平方;(3)斜边上的中线等于斜边的一半;(4)30°角所对的直角边等于斜边的一半.
4.如图,一根竹竿AB,斜靠在竖直的墙上,P是AB 的中点,A'B'表示竹竿AB 端沿墙上、下滑动过程中的某个位置,则在竹竿AB 滑动过程中 OP 的变化是 ( )
A.下滑时,OP 增大
B.上升时,OP 减小
C.无论怎样滑动,OP 不变
D.只要滑动,OP 就变化
5.如图,△ABC中,的平分线BE交AD于点 F,AG平分给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③∠EBC=∠C;④AG⊥EF.正确结论有 ( )
A.1个 B.2个 C.3个 D.4个
6.如图,已知△ABC是等腰三角形,AB=AC,点O是BC上任意一点,OE⊥AB,OF⊥AC,等腰三角形的腰长为4,面积为 ,则OE+OF的值为 ( )
A.1.5 C.2.5 D.3
7.已知一直角三角形,两边长为3和4,则斜边上的中线长为 .
8.如图,已知在△ABC中,AB=AC=2,∠B=15°.过点C作CD⊥BA,交BA的延长线于点D,则AD的长为 .
9.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为 .
10.如图,在△ABC中,∠B=∠C,AD是∠BAC的平分线,E、F分别是AB、AC 的中点,问DE、DF有什么样的关系 请说明理由.
11.如图,在等边三角形ABC中, ,AD、BE 相交于点 P,. 于点 Q.求证:
知识点 3 锐角三角函数
1.任意锐角的正弦、余弦和正切值都是正实数,并且0<<1,0<<1,>0.
2.同角三角函数的关系:
12.在Rt△ABC中,∠C=90°,如果那么AB的长是 ( )
A. B. C.
13.在Rt△ABC中,如果各边长度都扩大为原来的2倍,那么锐角A的正弦值 ( )
A.扩大2倍 B.缩小为原来的 C.扩大4倍 D.没有变化
14.若角α、β都是锐角,以下结论:
①若α<β,则<;②若α<β,则<;③若α<β,则<;④若α+β=90°,则=.其中正确的是 ( )
A.①② B.①②③ C.①③④ D.①②③④
15.如图,延长 Rt△ABC斜边AB到点 D,使BD=AB,连结CD,若 则 tanA 的值为 ( )
A. B.1 C. D.
16.已知α为锐角,且是一元二次方程 的一个根,则的值为 .
17.已知,正方形ABCD的边长为2,点P是直线CD上一点,若DP=1,则tan∠BPC的值是 .
18.设Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,根据下列所给条件,求∠B的三个三角函数值.
(1)a=5,c=13;(2)a:b=3:4.
19.在 中,已知α为一个锐角, 求 、的值.
知识点 4 特殊角的三角函数值及其用计算器求锐角三角函数值
20.已知α为锐角,且 则α等于 ( )
A.70° B.60° C.50° D.30°
21.计算的结果是 ( )
A.-1 B.0 D.1
22.在锐角△ABC中,则∠A= ( )
A.30° B.45° C.60°
23.用计算器求sin15°,sin25°,sin35°,sin45°,sin55°,sin65°,sin75°,sin85°的值,研究 的值随锐角α变化的规律,根据这个规律判断:若 则 ( )
A.30°<α<60°
24.用计算器求:( (精确到0.01)
(精确到0.01)
25.已知:s ,则a、b、c三者由大到小排列是 .
26.在△ABC中,∠A、∠B 均为锐角,若 则∠C= .
27.已知一个等腰三角形,顶角为120°,腰长为4cm,则该等腰三角形的面积为 .
28.已知锐角α,关于x的一元二次方程 有两个相等的实数根,求α的度数.
第24章基础复习(一)
1、A 2、30 3、3 4、C 5、C 6、B 或2 8 9、20
10.解:DE=DF.理由:
∵∠B=∠C,∴AB=AC.
∵AD是∠BAC的平分线,
∴AD⊥BC.
∵E、F分别是AB,AC的中点,
∴DE=DF.
11.证明:∵△ABC为等边三角形,
∴∠BAC=∠C=60°,AB=AC.
又∵AE=CD,
∴△ABE≌△CAD.
∴∠ABE=∠CAD,BE=AD,
∴∠BPQ =∠BAP +∠ABE =∠BAP +∠PAE =∠BAC=60°
又∵
即
12、B 13、D 14、C 15、A 17、2或
18.解:(1)在 中,
(2)设则
19.解:
或 (舍去).
即
20、A 21、B 22、D 23、A 24、(1)2.03 (2)2.11
25、c>a>b 26、120° 27、4cm
28.解:∵关于x的一元二次方程 有两个相等的实数根,
解得
知识点1 测量
利用阳光下物体的影子,镜子的反射,标杆的方法可以测量一些不易直接测量的物体的高度,其本质都是利用三角形相关知识.
1.如图,身高为1.5m的小华在打高尔夫球,他在阳光下的影长为2.1m ,此时他身后一棵树的影长为10.5m,则这棵树的高度为 ( )
A.7.5m B.8m C.14.7m D.15.75m
2.如图,B、C是河岸边两点,A是对岸岸边一点,测得∠ABC=45°,∠ACB=45°,BC=60m,则点A到岸边 BC 的距离是 m.
3.如图,已知零件的外径为30mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)测量零件的内孔直径AB.若()且量得CD=12mm,则零件的厚度x= mm.
知识点 2 直角三角形的性质
直角三角形的性质:(1)两锐角互余;(2)两条直角边的平方和等于斜边的平方;(3)斜边上的中线等于斜边的一半;(4)30°角所对的直角边等于斜边的一半.
4.如图,一根竹竿AB,斜靠在竖直的墙上,P是AB 的中点,A'B'表示竹竿AB 端沿墙上、下滑动过程中的某个位置,则在竹竿AB 滑动过程中 OP 的变化是 ( )
A.下滑时,OP 增大
B.上升时,OP 减小
C.无论怎样滑动,OP 不变
D.只要滑动,OP 就变化
5.如图,△ABC中,的平分线BE交AD于点 F,AG平分给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③∠EBC=∠C;④AG⊥EF.正确结论有 ( )
A.1个 B.2个 C.3个 D.4个
6.如图,已知△ABC是等腰三角形,AB=AC,点O是BC上任意一点,OE⊥AB,OF⊥AC,等腰三角形的腰长为4,面积为 ,则OE+OF的值为 ( )
A.1.5 C.2.5 D.3
7.已知一直角三角形,两边长为3和4,则斜边上的中线长为 .
8.如图,已知在△ABC中,AB=AC=2,∠B=15°.过点C作CD⊥BA,交BA的延长线于点D,则AD的长为 .
9.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为 .
10.如图,在△ABC中,∠B=∠C,AD是∠BAC的平分线,E、F分别是AB、AC 的中点,问DE、DF有什么样的关系 请说明理由.
11.如图,在等边三角形ABC中, ,AD、BE 相交于点 P,. 于点 Q.求证:
知识点 3 锐角三角函数
1.任意锐角的正弦、余弦和正切值都是正实数,并且0<<1,0<<1,>0.
2.同角三角函数的关系:
12.在Rt△ABC中,∠C=90°,如果那么AB的长是 ( )
A. B. C.
13.在Rt△ABC中,如果各边长度都扩大为原来的2倍,那么锐角A的正弦值 ( )
A.扩大2倍 B.缩小为原来的 C.扩大4倍 D.没有变化
14.若角α、β都是锐角,以下结论:
①若α<β,则<;②若α<β,则<;③若α<β,则<;④若α+β=90°,则=.其中正确的是 ( )
A.①② B.①②③ C.①③④ D.①②③④
15.如图,延长 Rt△ABC斜边AB到点 D,使BD=AB,连结CD,若 则 tanA 的值为 ( )
A. B.1 C. D.
16.已知α为锐角,且是一元二次方程 的一个根,则的值为 .
17.已知,正方形ABCD的边长为2,点P是直线CD上一点,若DP=1,则tan∠BPC的值是 .
18.设Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,根据下列所给条件,求∠B的三个三角函数值.
(1)a=5,c=13;(2)a:b=3:4.
19.在 中,已知α为一个锐角, 求 、的值.
知识点 4 特殊角的三角函数值及其用计算器求锐角三角函数值
20.已知α为锐角,且 则α等于 ( )
A.70° B.60° C.50° D.30°
21.计算的结果是 ( )
A.-1 B.0 D.1
22.在锐角△ABC中,则∠A= ( )
A.30° B.45° C.60°
23.用计算器求sin15°,sin25°,sin35°,sin45°,sin55°,sin65°,sin75°,sin85°的值,研究 的值随锐角α变化的规律,根据这个规律判断:若 则 ( )
A.30°<α<60°
24.用计算器求:( (精确到0.01)
(精确到0.01)
25.已知:s ,则a、b、c三者由大到小排列是 .
26.在△ABC中,∠A、∠B 均为锐角,若 则∠C= .
27.已知一个等腰三角形,顶角为120°,腰长为4cm,则该等腰三角形的面积为 .
28.已知锐角α,关于x的一元二次方程 有两个相等的实数根,求α的度数.
第24章基础复习(一)
1、A 2、30 3、3 4、C 5、C 6、B 或2 8 9、20
10.解:DE=DF.理由:
∵∠B=∠C,∴AB=AC.
∵AD是∠BAC的平分线,
∴AD⊥BC.
∵E、F分别是AB,AC的中点,
∴DE=DF.
11.证明:∵△ABC为等边三角形,
∴∠BAC=∠C=60°,AB=AC.
又∵AE=CD,
∴△ABE≌△CAD.
∴∠ABE=∠CAD,BE=AD,
∴∠BPQ =∠BAP +∠ABE =∠BAP +∠PAE =∠BAC=60°
又∵
即
12、B 13、D 14、C 15、A 17、2或
18.解:(1)在 中,
(2)设则
19.解:
或 (舍去).
即
20、A 21、B 22、D 23、A 24、(1)2.03 (2)2.11
25、c>a>b 26、120° 27、4cm
28.解:∵关于x的一元二次方程 有两个相等的实数根,
解得
