17.1 勾股定理 知识点分类训练(含答案)初中数学人教版八年级下册
文档属性
| 名称 | 17.1 勾股定理 知识点分类训练(含答案)初中数学人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 258.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 15:50:14 | ||
图片预览


文档简介
第十七章 勾股定理
17.1 勾股定理
第1课时 勾股定理
课堂探究 例题点拨
知识点1 勾股定理的证明
例1 (教材P23探究变式)4个全等的直角三角形的两直角边长分别为,,斜边长为.现把它们适当地拼合,可以得到如图所示的图形,利用这个图形可以验证勾股定理,你能说明其中的道理吗?请试一试.
例1图
【变式1】 [2023扬州]我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成.如图,直角三角形的两直角边长分别为,,斜边长为,若,,则每个直角三角形的面积为__.
变式1图
【变式2】 [2023黄冈]如图是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成的一个大正方形.设图中,,连接,.若与的面积相等,则____.
变式2图
知识点2 利用勾股定理进行计算
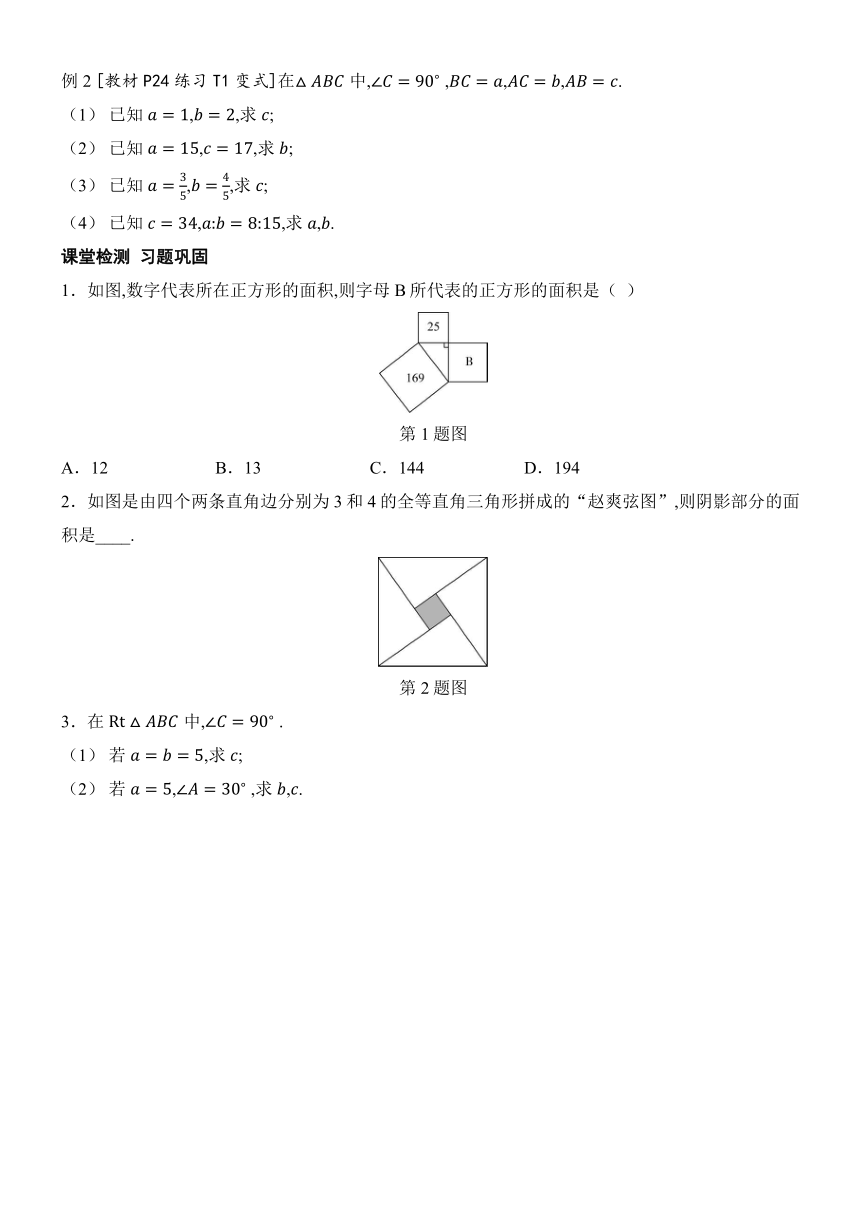
例2 [教材P24练习T1变式]在中, ,,,.
(1) 已知,,求;
(2) 已知,,求;
(3) 已知,,求;
(4) 已知,,求,.
课堂检测 习题巩固
1.如图,数字代表所在正方形的面积,则字母B所代表的正方形的面积是( )
第1题图
A.12 B.13 C.144 D.194
2.如图是由四个两条直角边分别为3和4的全等直角三角形拼成的“赵爽弦图”,则阴影部分的面积是____.
第2题图
3.在中, .
(1) 若,求;
(2) 若, ,求,.
第2课时 勾股定理的实际应用
课堂探究 例题点拨
知识点1 勾股定理在实际问题中的应用
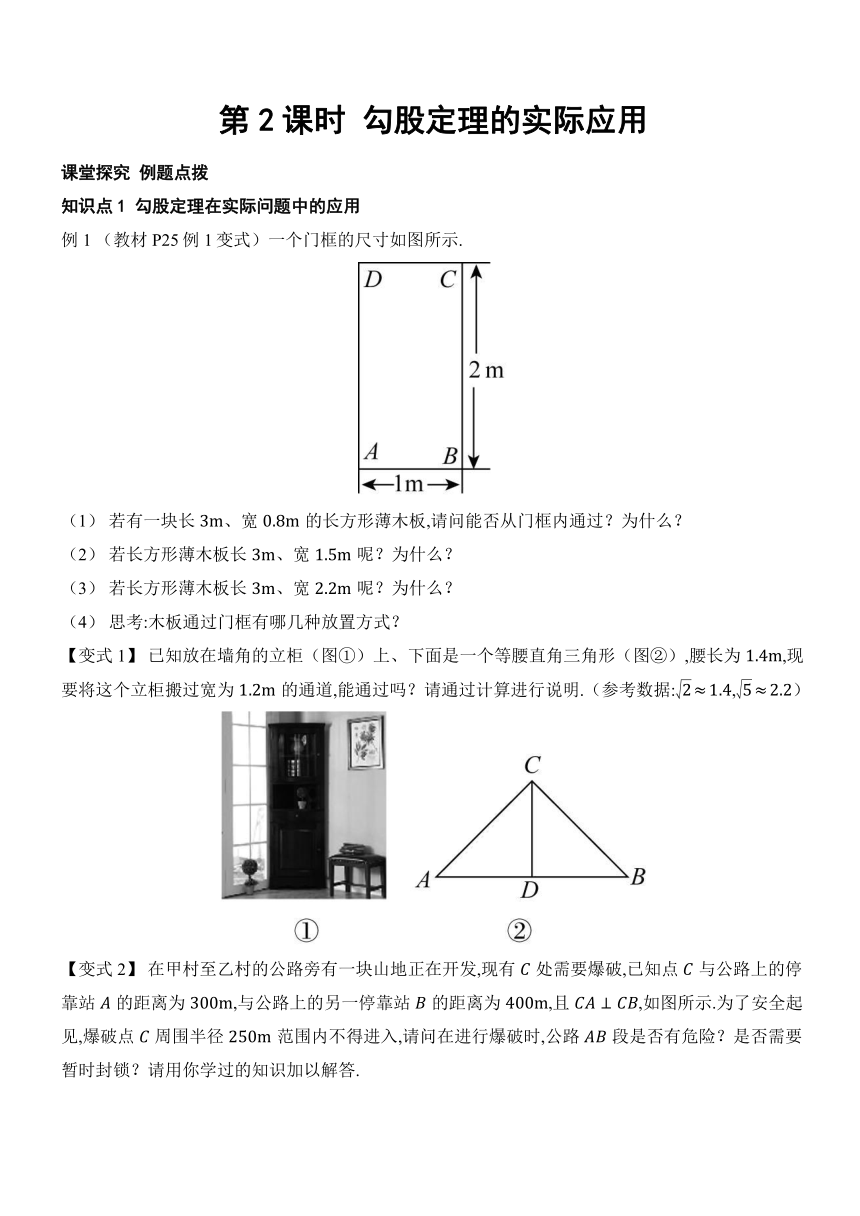
例1 (教材P25例1变式)一个门框的尺寸如图所示.
(1) 若有一块长、宽的长方形薄木板,请问能否从门框内通过?为什么?
(2) 若长方形薄木板长、宽呢?为什么?
(3) 若长方形薄木板长、宽呢?为什么?
(4) 思考:木板通过门框有哪几种放置方式?
【变式1】 已知放在墙角的立柜(图①)上、下面是一个等腰直角三角形(图②),腰长为,现要将这个立柜搬过宽为的通道,能通过吗?请通过计算进行说明.(参考数据:,)
【变式2】 在甲村至乙村的公路旁有一块山地正在开发,现有处需要爆破,已知点与公路上的停靠站的距离为,与公路上的另一停靠站的距离为,且,如图所示.为了安全起见,爆破点周围半径范围内不得进入,请问在进行爆破时,公路段是否有危险?是否需要暂时封锁?请用你学过的知识加以解答.
例2 如图,一架梯子长,斜靠在一面墙上的点处,梯子底端在点处且离墙的距离是.
(1) 这个梯子的顶端距地面多高?
(2) 如果梯子的顶端下滑了到达点处,那么梯子的底端在水平方向滑动了几米?
知识点2 利用勾股定理求两点间的距离
例3 (教材P26练习T2变式)如图,在平面直角坐标系中,,,,则,两点间的距离是______;,两点间的距离是____;,两点间的距离是____.
课堂检测 习题巩固
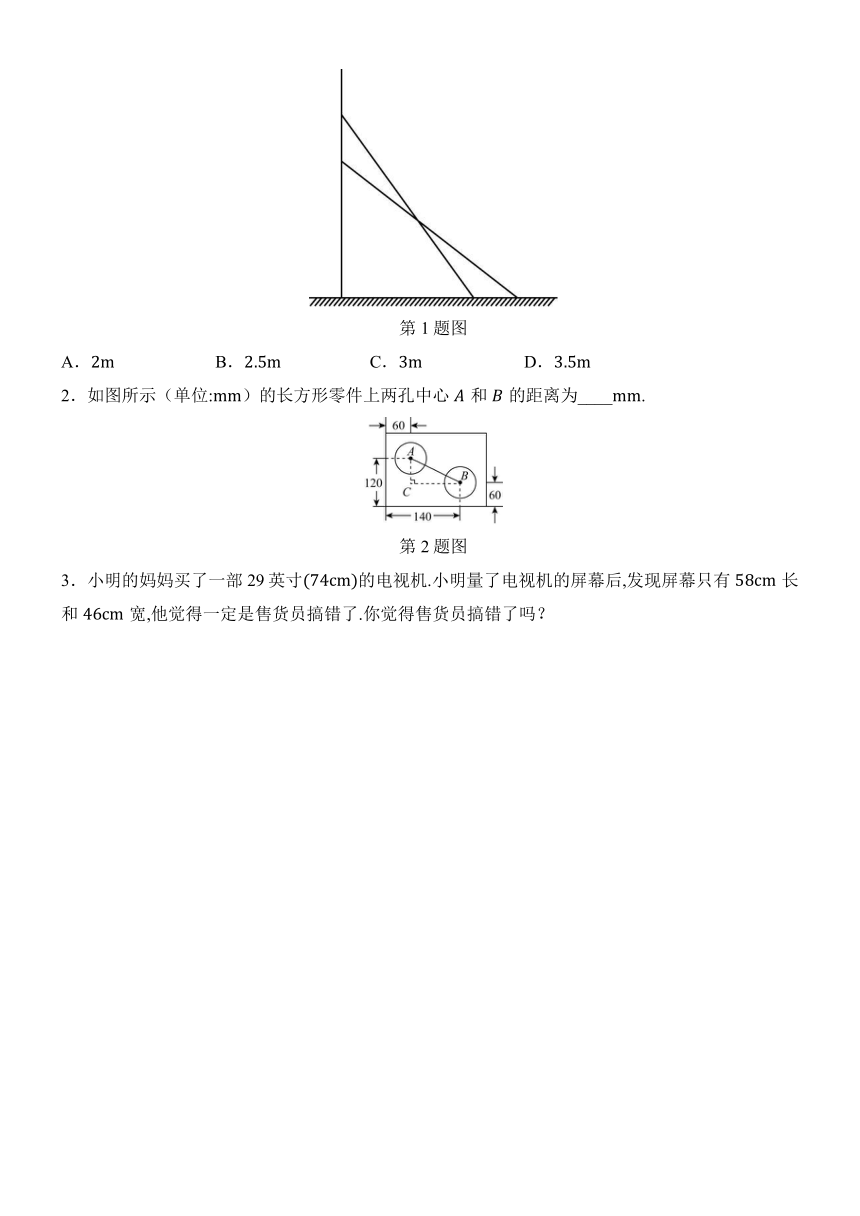
1.如图,一架长为的梯子斜靠在一面墙上,梯子底端离墙,如果梯子的顶端下滑了,那么梯子底部在水平方向滑动了( )
第1题图
A. B. C. D.
2.如图所示(单位:)的长方形零件上两孔中心和的距离为____.
第2题图
3.小明的妈妈买了一部29英寸的电视机.小明量了电视机的屏幕后,发现屏幕只有长和宽,他觉得一定是售货员搞错了.你觉得售货员搞错了吗?
第3课时 利用勾股定理证明与作图
课堂探究 例题点拨
知识点1 用勾股定理证明“”定理
例1 (教材P26思考变式)我们知道“两边和一角分别相等的两个三角形不一定全等”,如图①,,,,但与却不全等.但是如果是两个直角三角形呢?如图②,,, ,和全等吗?
(1) 根据图②完成以下证明和阅读:
在和中, ,
根据勾股定理,得,__________________.
,,________.
________(________).
归纳:斜边和一条直角边相等的两个直角三角形全等,简称为“斜边直角边”或“”.
几何语言如下:
在和中, ,
,,
.
(2) 如图③,已知 ,.求证:平分.
知识点2 画线段表示无理数
例2 作图:请在如图所示的数轴上作出表示的点(保留作图痕迹,不写作法).
【变式】 图①、②中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.
(1) 在图①中以格点为顶点画一个面积为5的正方形;
(2) 如图②,,,是小正方形的顶点,求的度数.
知识点3 等腰三角形中的勾股定理
例3 (教材P27练习T2变式)如图,在中,,,求该等腰三角形底边上的高与面积.
课堂检测 习题巩固
1.如图,数轴上点所表示的数为,则的值是( )
第1题图
A. B. C. D.
2.[2024沈阳模拟]如图,,,要根据“”证明,还应添加一个条件是( )
第2题图
A. B. C. D.
3.在数轴上作出表示的点(不写作法,保留作图痕迹).
第十七章 勾股定理
17.1 勾股定理
第1课时 勾股定理
课堂探究 例题点拨
知识点1 勾股定理的证明
例1 解:图形的总面积可以表示为,
图形的总面积也可以表示为,
,
.
【变式1】 96
【变式2】 3
知识点2 利用勾股定理进行计算
例2 (1) 解:.
(2) .
(3) .
(4) 设,则.
由勾股定理,得,解得或(不合题意,舍去).
,.
课堂检测 习题巩固
1.C
2.1
3.(1) 解:.
(2) 在中, ,, ,
,.
第2课时 勾股定理的实际应用
课堂探究 例题点拨
知识点1 勾股定理在实际问题中的应用
例1 (1) 解:能从门框内通过.理由如下:
,
一块长、宽的长方形薄木板,能从门框内通过.
(2) 能从门框内通过.理由如下:
,
长方形薄木板长、宽,能从门框内通过.
(3) 能从门框内通过.理由如下:
在中,,
长方形薄木板长、宽,能从门框内通过.
(4) 木板通过门框的放置方式有:水平放置、竖直放置、沿门框对角线放置.
【变式1】 解:等腰的腰长为,
,
.
,
,
.
,
能通过.
【变式2】 解:如答图,过点作于点.
,, ,
.
,
.
,故公路段有危险,因此段公路需要暂时封锁.
变式2答图
例2 (1) 解:由题意,得,,
.
答:这个梯子的顶端距地面.
(2) 由题意,得,
,
.
答:梯子的底端在水平方向滑动了.
知识点2 利用勾股定理求两点间的距离
例3 ; 5; 5
课堂检测 习题巩固
1.A
2.100
3.解: ,长和宽的电视机的屏幕的对角线大约为, 售货员没有搞错.我们通常所说的29英寸的电视机,是指电视机的屏幕的对角线的长度.
第3课时 利用勾股定理证明与作图
课堂探究 例题点拨
知识点1 用勾股定理证明“”定理
例1 (1) ; ; ;
(2) 证明: ,
和是直角三角形.
在和中,
,
,平分.
知识点2 画线段表示无理数
例2 解:如答图,就是表示的点.
例2答图
【变式】 (1) 解:如答图①.
变式答图
(2) 如答图②,连接,设点右侧的格点为,点下侧的格点为,则,
变式答图
且易证.
.
.
.
知识点3 等腰三角形中的勾股定理
例3 解:如答图,过点作于点.
,,
,
即等腰三角形底边上的高为.
.
例3答图
课堂检测 习题巩固
1.B 2.C
3.解:如答图,点即为所求.
第3题答图
17.1 勾股定理
第1课时 勾股定理
课堂探究 例题点拨
知识点1 勾股定理的证明
例1 (教材P23探究变式)4个全等的直角三角形的两直角边长分别为,,斜边长为.现把它们适当地拼合,可以得到如图所示的图形,利用这个图形可以验证勾股定理,你能说明其中的道理吗?请试一试.
例1图
【变式1】 [2023扬州]我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成.如图,直角三角形的两直角边长分别为,,斜边长为,若,,则每个直角三角形的面积为__.
变式1图
【变式2】 [2023黄冈]如图是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成的一个大正方形.设图中,,连接,.若与的面积相等,则____.
变式2图
知识点2 利用勾股定理进行计算
例2 [教材P24练习T1变式]在中, ,,,.
(1) 已知,,求;
(2) 已知,,求;
(3) 已知,,求;
(4) 已知,,求,.
课堂检测 习题巩固
1.如图,数字代表所在正方形的面积,则字母B所代表的正方形的面积是( )
第1题图
A.12 B.13 C.144 D.194
2.如图是由四个两条直角边分别为3和4的全等直角三角形拼成的“赵爽弦图”,则阴影部分的面积是____.
第2题图
3.在中, .
(1) 若,求;
(2) 若, ,求,.
第2课时 勾股定理的实际应用
课堂探究 例题点拨
知识点1 勾股定理在实际问题中的应用
例1 (教材P25例1变式)一个门框的尺寸如图所示.
(1) 若有一块长、宽的长方形薄木板,请问能否从门框内通过?为什么?
(2) 若长方形薄木板长、宽呢?为什么?
(3) 若长方形薄木板长、宽呢?为什么?
(4) 思考:木板通过门框有哪几种放置方式?
【变式1】 已知放在墙角的立柜(图①)上、下面是一个等腰直角三角形(图②),腰长为,现要将这个立柜搬过宽为的通道,能通过吗?请通过计算进行说明.(参考数据:,)
【变式2】 在甲村至乙村的公路旁有一块山地正在开发,现有处需要爆破,已知点与公路上的停靠站的距离为,与公路上的另一停靠站的距离为,且,如图所示.为了安全起见,爆破点周围半径范围内不得进入,请问在进行爆破时,公路段是否有危险?是否需要暂时封锁?请用你学过的知识加以解答.
例2 如图,一架梯子长,斜靠在一面墙上的点处,梯子底端在点处且离墙的距离是.
(1) 这个梯子的顶端距地面多高?
(2) 如果梯子的顶端下滑了到达点处,那么梯子的底端在水平方向滑动了几米?
知识点2 利用勾股定理求两点间的距离
例3 (教材P26练习T2变式)如图,在平面直角坐标系中,,,,则,两点间的距离是______;,两点间的距离是____;,两点间的距离是____.
课堂检测 习题巩固
1.如图,一架长为的梯子斜靠在一面墙上,梯子底端离墙,如果梯子的顶端下滑了,那么梯子底部在水平方向滑动了( )
第1题图
A. B. C. D.
2.如图所示(单位:)的长方形零件上两孔中心和的距离为____.
第2题图
3.小明的妈妈买了一部29英寸的电视机.小明量了电视机的屏幕后,发现屏幕只有长和宽,他觉得一定是售货员搞错了.你觉得售货员搞错了吗?
第3课时 利用勾股定理证明与作图
课堂探究 例题点拨
知识点1 用勾股定理证明“”定理
例1 (教材P26思考变式)我们知道“两边和一角分别相等的两个三角形不一定全等”,如图①,,,,但与却不全等.但是如果是两个直角三角形呢?如图②,,, ,和全等吗?
(1) 根据图②完成以下证明和阅读:
在和中, ,
根据勾股定理,得,__________________.
,,________.
________(________).
归纳:斜边和一条直角边相等的两个直角三角形全等,简称为“斜边直角边”或“”.
几何语言如下:
在和中, ,
,,
.
(2) 如图③,已知 ,.求证:平分.
知识点2 画线段表示无理数
例2 作图:请在如图所示的数轴上作出表示的点(保留作图痕迹,不写作法).
【变式】 图①、②中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.
(1) 在图①中以格点为顶点画一个面积为5的正方形;
(2) 如图②,,,是小正方形的顶点,求的度数.
知识点3 等腰三角形中的勾股定理
例3 (教材P27练习T2变式)如图,在中,,,求该等腰三角形底边上的高与面积.
课堂检测 习题巩固
1.如图,数轴上点所表示的数为,则的值是( )
第1题图
A. B. C. D.
2.[2024沈阳模拟]如图,,,要根据“”证明,还应添加一个条件是( )
第2题图
A. B. C. D.
3.在数轴上作出表示的点(不写作法,保留作图痕迹).
第十七章 勾股定理
17.1 勾股定理
第1课时 勾股定理
课堂探究 例题点拨
知识点1 勾股定理的证明
例1 解:图形的总面积可以表示为,
图形的总面积也可以表示为,
,
.
【变式1】 96
【变式2】 3
知识点2 利用勾股定理进行计算
例2 (1) 解:.
(2) .
(3) .
(4) 设,则.
由勾股定理,得,解得或(不合题意,舍去).
,.
课堂检测 习题巩固
1.C
2.1
3.(1) 解:.
(2) 在中, ,, ,
,.
第2课时 勾股定理的实际应用
课堂探究 例题点拨
知识点1 勾股定理在实际问题中的应用
例1 (1) 解:能从门框内通过.理由如下:
,
一块长、宽的长方形薄木板,能从门框内通过.
(2) 能从门框内通过.理由如下:
,
长方形薄木板长、宽,能从门框内通过.
(3) 能从门框内通过.理由如下:
在中,,
长方形薄木板长、宽,能从门框内通过.
(4) 木板通过门框的放置方式有:水平放置、竖直放置、沿门框对角线放置.
【变式1】 解:等腰的腰长为,
,
.
,
,
.
,
能通过.
【变式2】 解:如答图,过点作于点.
,, ,
.
,
.
,故公路段有危险,因此段公路需要暂时封锁.
变式2答图
例2 (1) 解:由题意,得,,
.
答:这个梯子的顶端距地面.
(2) 由题意,得,
,
.
答:梯子的底端在水平方向滑动了.
知识点2 利用勾股定理求两点间的距离
例3 ; 5; 5
课堂检测 习题巩固
1.A
2.100
3.解: ,长和宽的电视机的屏幕的对角线大约为, 售货员没有搞错.我们通常所说的29英寸的电视机,是指电视机的屏幕的对角线的长度.
第3课时 利用勾股定理证明与作图
课堂探究 例题点拨
知识点1 用勾股定理证明“”定理
例1 (1) ; ; ;
(2) 证明: ,
和是直角三角形.
在和中,
,
,平分.
知识点2 画线段表示无理数
例2 解:如答图,就是表示的点.
例2答图
【变式】 (1) 解:如答图①.
变式答图
(2) 如答图②,连接,设点右侧的格点为,点下侧的格点为,则,
变式答图
且易证.
.
.
.
知识点3 等腰三角形中的勾股定理
例3 解:如答图,过点作于点.
,,
,
即等腰三角形底边上的高为.
.
例3答图
课堂检测 习题巩固
1.B 2.C
3.解:如答图,点即为所求.
第3题答图
