17.1 勾股定理 第1课时 分层训练(含答案)初中数学人教版八年级下册
文档属性
| 名称 | 17.1 勾股定理 第1课时 分层训练(含答案)初中数学人教版八年级下册 | 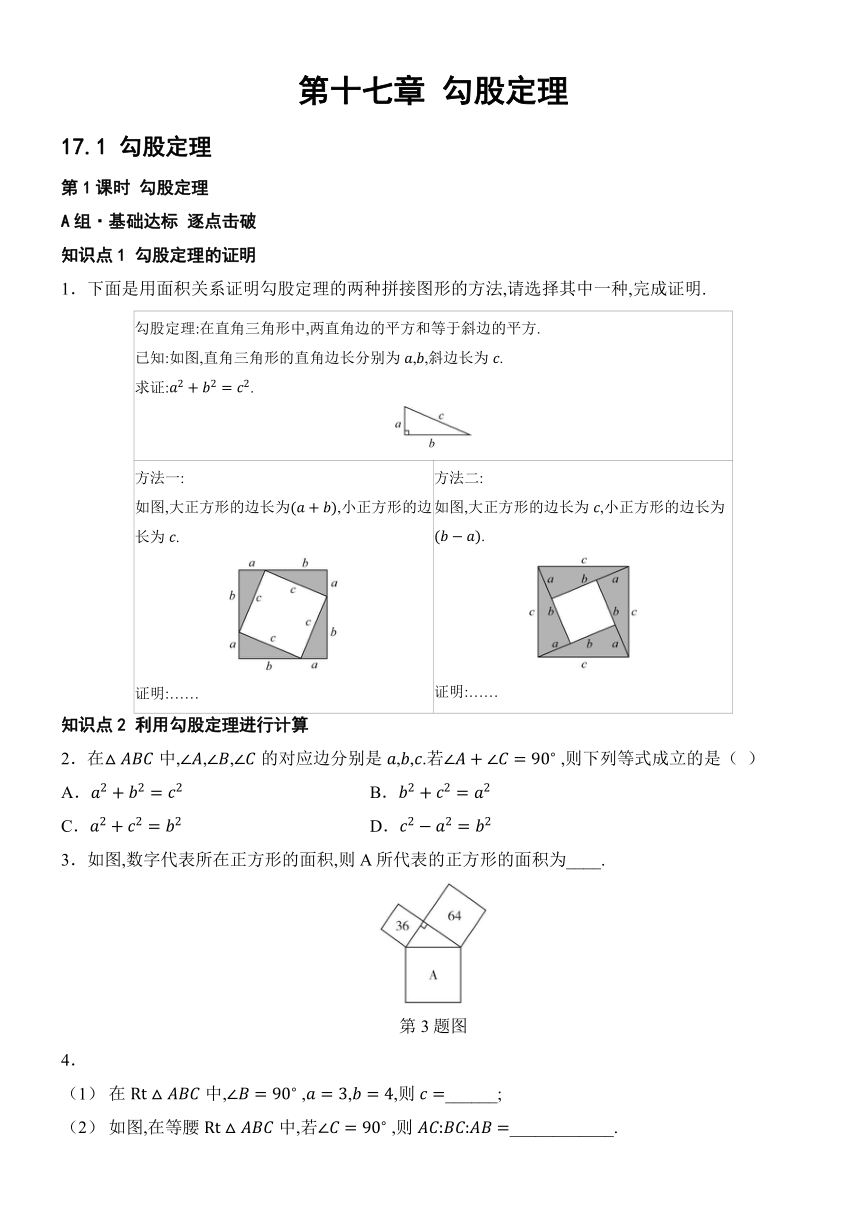 | |
| 格式 | docx | ||
| 文件大小 | 104.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 15:37:43 | ||
图片预览


文档简介
第十七章 勾股定理
17.1 勾股定理
第1课时 勾股定理
A组·基础达标 逐点击破
知识点1 勾股定理的证明
1.下面是用面积关系证明勾股定理的两种拼接图形的方法,请选择其中一种,完成证明.
勾股定理:在直角三角形中,两直角边的平方和等于斜边的平方. 已知:如图,直角三角形的直角边长分别为,,斜边长为. 求证:.
方法一: 如图,大正方形的边长为,小正方形的边长为. 证明:…… 方法二: 如图,大正方形的边长为,小正方形的边长为. 证明:……
知识点2 利用勾股定理进行计算
2.在中,,,的对应边分别是,,.若 ,则下列等式成立的是( )
A. B.
C. D.
3.如图,数字代表所在正方形的面积,则A所代表的正方形的面积为____.
第3题图
4.
(1) 在中, ,,,则______;
(2) 如图,在等腰中,若 ,则____________.
第4(2)题图
5.在中, ,,,.
(1) 已知,求;
(2) 已知,,求;
(3) 已知,,求.
易错点 边的类型不确定时漏解
6.若直角三角形的两边长分别为12和5,则第三边长为______________.
B组·能力提升 强化突破
7.[2024长沙模拟]如图,在中, ,,点在上,,,则的长为__.
8.[2022衡阳模拟]学习勾股定理之后,同学们发现证明勾股定理有很多方法.某同学提出了一种证明勾股定理的方法:如图①,是正方形边上一点,连接,得到,三边分别为,,,将裁剪拼接至位置,如图②所示,该同学用图①、图②的面积不变证明了勾股定理.请你写出该方法证明勾股定理的过程.
① ②
C组·核心素养拓展 素养渗透
9.[2024南通]【模型观念】“赵爽弦图”巧妙利用面积关系证明了勾股定理.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形.设直角三角形的直角边长分别为,.若小正方形的面积为5,,则大正方形的面积为( )
A.12 B.13 C.14 D.15
10.[2024大庆]【模型观念】如图①,直角三角形的两个锐角分别是 和 ,其三边上分别有一个正方形.执行下面的操作:由两个小正方形向外分别作锐角为 和 的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形.图②是1次操作后的图形.图③是重复上述步骤若干次后得到的图形,人们把它称为“毕达哥拉斯树”.若图①中的直角三角形斜边长为2,则10次操作后图形中所有正方形的面积和为__.
11.【模型观念】如图,将八个全等的直角三角形紧密地拼接,记图中正方形,正方形,正方形的面积分别为,,,若,则________.
第十七章 勾股定理
17.1 勾股定理
第1课时 勾股定理
A组·基础达标 逐点击破
知识点1 勾股定理的证明
1.证明:(方法一)由题图可得,
,
化简,得.
(方法二)由题图可得,
,
化简,得.
知识点2 利用勾股定理进行计算
2.C
3.100
4.(1)
(2)
5.(1) 解: ,,
.
(2) ,,,
.
(3) ,,,
.
易错点 边的类型不确定时漏解
6.13或
B组·能力提升 强化突破
7.16
8.证明:如答图,连接.
,
.
,
,
,
.
,
.
,
,
为等腰直角三角形,
.
,
,
,.
第8题答图
C组·核心素养拓展 素养渗透
9.B
10.48
11.
[解析]设四边形的面积为,其余八个全等的三角形面积分别为.
正方形,正方形,正方形的面积分别为,,,且,
,,,
,
,
.
17.1 勾股定理
第1课时 勾股定理
A组·基础达标 逐点击破
知识点1 勾股定理的证明
1.下面是用面积关系证明勾股定理的两种拼接图形的方法,请选择其中一种,完成证明.
勾股定理:在直角三角形中,两直角边的平方和等于斜边的平方. 已知:如图,直角三角形的直角边长分别为,,斜边长为. 求证:.
方法一: 如图,大正方形的边长为,小正方形的边长为. 证明:…… 方法二: 如图,大正方形的边长为,小正方形的边长为. 证明:……
知识点2 利用勾股定理进行计算
2.在中,,,的对应边分别是,,.若 ,则下列等式成立的是( )
A. B.
C. D.
3.如图,数字代表所在正方形的面积,则A所代表的正方形的面积为____.
第3题图
4.
(1) 在中, ,,,则______;
(2) 如图,在等腰中,若 ,则____________.
第4(2)题图
5.在中, ,,,.
(1) 已知,求;
(2) 已知,,求;
(3) 已知,,求.
易错点 边的类型不确定时漏解
6.若直角三角形的两边长分别为12和5,则第三边长为______________.
B组·能力提升 强化突破
7.[2024长沙模拟]如图,在中, ,,点在上,,,则的长为__.
8.[2022衡阳模拟]学习勾股定理之后,同学们发现证明勾股定理有很多方法.某同学提出了一种证明勾股定理的方法:如图①,是正方形边上一点,连接,得到,三边分别为,,,将裁剪拼接至位置,如图②所示,该同学用图①、图②的面积不变证明了勾股定理.请你写出该方法证明勾股定理的过程.
① ②
C组·核心素养拓展 素养渗透
9.[2024南通]【模型观念】“赵爽弦图”巧妙利用面积关系证明了勾股定理.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形.设直角三角形的直角边长分别为,.若小正方形的面积为5,,则大正方形的面积为( )
A.12 B.13 C.14 D.15
10.[2024大庆]【模型观念】如图①,直角三角形的两个锐角分别是 和 ,其三边上分别有一个正方形.执行下面的操作:由两个小正方形向外分别作锐角为 和 的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形.图②是1次操作后的图形.图③是重复上述步骤若干次后得到的图形,人们把它称为“毕达哥拉斯树”.若图①中的直角三角形斜边长为2,则10次操作后图形中所有正方形的面积和为__.
11.【模型观念】如图,将八个全等的直角三角形紧密地拼接,记图中正方形,正方形,正方形的面积分别为,,,若,则________.
第十七章 勾股定理
17.1 勾股定理
第1课时 勾股定理
A组·基础达标 逐点击破
知识点1 勾股定理的证明
1.证明:(方法一)由题图可得,
,
化简,得.
(方法二)由题图可得,
,
化简,得.
知识点2 利用勾股定理进行计算
2.C
3.100
4.(1)
(2)
5.(1) 解: ,,
.
(2) ,,,
.
(3) ,,,
.
易错点 边的类型不确定时漏解
6.13或
B组·能力提升 强化突破
7.16
8.证明:如答图,连接.
,
.
,
,
,
.
,
.
,
,
为等腰直角三角形,
.
,
,
,.
第8题答图
C组·核心素养拓展 素养渗透
9.B
10.48
11.
[解析]设四边形的面积为,其余八个全等的三角形面积分别为.
正方形,正方形,正方形的面积分别为,,,且,
,,,
,
,
.
